基于三维坐标测量轨道几何形位的计算模型*
2017-03-07何越磊
黎 桂 何越磊
(上海工程技术大学城市轨道交通学院,201620,上海∥第一作者,硕士研究生)
基于三维坐标测量轨道几何形位的计算模型*
黎 桂 何越磊
(上海工程技术大学城市轨道交通学院,201620,上海∥第一作者,硕士研究生)
为改进基于CPⅢ轨道控制网测量技术的地铁无砟轨道几何形位精调的测量精度与效率,提出一种基于三维坐标测量轨道几何形位的方法。通过对轨道几何形位检测点进行三维坐标测量,以轨道控制网CPⅢ点作为测量基准点,采用轨道几何形位与检测点的三维解析几何关系,建立三维坐标测量轨道几何形位的计算模型。现场无砟轨道试验段的测试结果表明,三维坐标测量可有效对轨道几何形位进行测量,测量精度满足规范要求的无砟轨道几何形位测量精度指标。
地铁; 轨道几何形位; 三维坐标测量; 计算模型
Author′s address School of Urban Rail Transportation, Shanghai University of Engineering Science,201620,Shanghai,China
轨道是保证轨道交通列车平稳、安全运行的基础,其几何形位的检测精度会影响列车的运行状态[1]。随着地铁的发展,对列车的舒适性和平稳性的要求越来越高,为确保地铁无砟轨道精度满足线路平顺性要求,近年来我国地铁开始采取高速铁路无砟轨道精测技术,在无砟轨道施工初期布设高精度的CPⅢ轨道控制网。例如,上海轨道交通16号线(设计速度为120 km/h)在无砟轨道铺设作业中,采用高铁CPⅢ轨道控制网测量技术对轨道几何形位进行精调测量。
目前,国内外对基于CPⅢ轨道控制网测量技术的无砟轨道几何形位的静态检测方式,主要以瑞士GRP1000轨检小车[2]和德国GEDO CE轨道几何状态测量仪[3]为代表。这两种检测方式都是通过移动轨检小车对钢轨进行逐点测量,利用全站仪对轨检小车的位置进行定位,从而测量出检测点的轨道几何形位参数[4]。此检测方法为无砟轨道几何形位精测提供了重要的技术支持。
然而,随着地铁建设与运营线路的日益增加,以及检测作业时间较短,使轨道检测作业变得繁重,常规基于全站仪的轨检小车检测方式在测量精度、测量效率等方面有待进一步改善。因此,有必要改进无砟轨道几何形位静态检测技术,研究出一种能够满足地铁无砟轨道几何形位高精度、高效率检测要求的测量方法。
本文采用三维坐标测量仪对钢轨检测点进行三维坐标测量,通过空间三维解析几何关系建立三维坐标计算模型,计算轨道几何形位参数,并对解析计算模型进行了试验验证。
1 三维坐标测量计算模型
基于三维坐标的轨道几何形位测量方法,是对检测点进行三维坐标测量,并根据检测点的三维坐标进行轨道几何形位参数计算。
如图1所示,选取钢轨顶面与轨顶面下16 mm侧面的垂直交点为轨道几何形位检测点。每根轨枕的上方均设置2对轨道几何形位检测点,检测点的间距等于轨枕间距。设轨道几何形位检测点的三维坐标均位于同一空间三维直角坐标系下,点Pi(xi,yi,zi)、Pi+1(xi+1,yi+1,zi+1)、Pi+2(xi+2,yi+2,zi+2)分别是左股钢轨第i、i+1、i+2个检测点,i=1,2,…,n;点Pj(xj,yj,zj)、Pj+1(xj+1,yj+1,zj+1)、Pj+2(xj+2,yj+2,zj+2)分别是右股钢轨第j、j+1、j+2个检测点,j=1,2,…,n。

图1 轨道几何形位检测点的位置
1.1 轨距计算模型
轨距是指轨道两股钢轨内侧轨踏面下16 mm处两工作边之间的最小距离。轨距是通过左右两股钢轨的轨道几何形位检测点三维坐标计算的,这就要求左右两个检测点的里程是相等的,即xi=xj。但在对轨道几何形位检测点的三维坐标进行采集作业中,同一轨枕上的左右两股钢轨的轨道几何形位检测点不能确保在同一里程上,如图2所示。因此,至少要根据3个轨道几何形位检测点计算轨距。
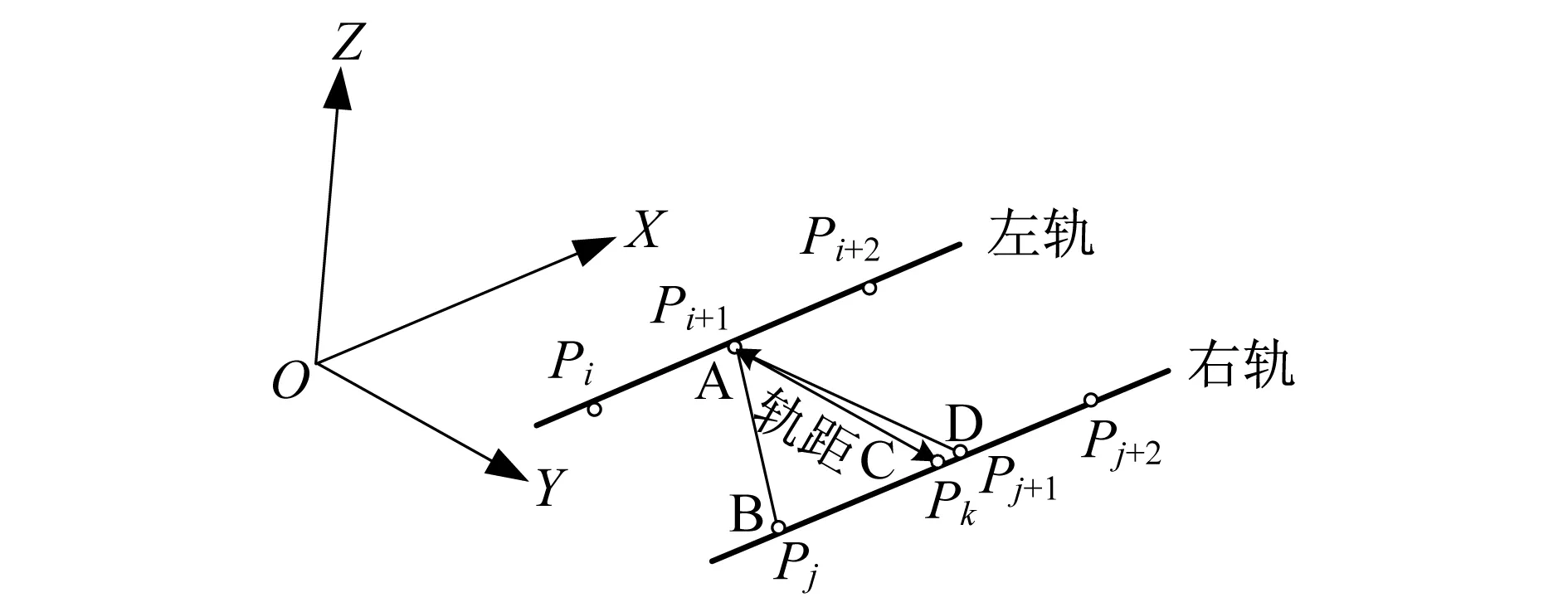
图2 轨距计算模型
定义图2中的空间三维直角坐标系O-XYZ为:X轴正向平行于里程正方向,Y轴正向垂直于X轴并指向右股钢轨,Z轴正向为平行于钢轨顶端向上并与XOY组成空间右手坐标系。即x为检测点的里程坐标,y为检测点的横向坐标,z为检测点的垂向坐标。
由于存在轨底坡,为使车轮载荷作用力集中在钢轨顶面的中部,提高钢轨的横向稳定性,在直线上的钢轨也要适当地向内倾斜[5]。为了满足无砟轨道几何形位检测的高精度要求,需考虑轨底坡的影响。钢轨倾斜状态下的轨距检测示意图如图3所示。

图3 轨距测量示意图
图3中,Pi+1、P′i+1分别为左股钢轨的内侧检测点和外侧检测点,Pk、P′k分别为右股钢轨的内侧检测点和外侧检测点,α、β分别为左右两股钢轨的倾斜角,则轨距S与检测点三维坐标的几何关系为:
(1)
1.2 水平和超高的计算模型
水平是指轨道左右两股钢轨顶面的相对高差。为使两股钢轨在列车车轮作用力下受力均匀,保证列车平稳运行,两股钢轨顶面在直线段时应保持同一水平,在曲线段时应按相关设计标准要求设置钢轨超高。水平和超高检测示意图如图4所示。

图4 水平和超高测量示意图
由图4可得水平和超高与检测点三维坐标的几何关系为:
(2)
1.3 高低和轨向的计算模型
我国无砟轨道高低和轨向的不平顺检测方法主要采用中波不平顺检测法和长波不平顺检测法[6-8]。
中波不平顺检测法采用基线长为48个轨枕间距的弦线,每间隔8个轨枕间距设置一对轨道几何形位检测点。以轨枕P25与P33的正矢值h25和h33为例,中波不平顺通过轨枕P25与P33处两检测点间实测正矢值与设计正矢值的差值计算得到,即:
(3)
长波不平顺检测法采用基线长为480个轨枕间距弦线,每间隔240个轨枕间距设置一对轨道几何形位检测点。以轨枕P25和P265的正矢值h25和h265为例,长波不平顺通过P25和P265处两检测点间实测正矢值与设计正矢值的差值计算得到,即:
(4)
将式(3)和式(4)改写成式(5):
(5)
由式(5)可知,轨道中波和长波的高低、轨向不平顺,实质是弦长48个轨枕、480个轨枕弦范围内,间隔为8个轨枕、240个轨枕两检测点实测正矢值和设计正矢值的差值。
基线长为48个轨枕间距的弦各检测点高低、轨向的实测正矢值和设计正矢值的偏差计算示意图如图5所示[8]。
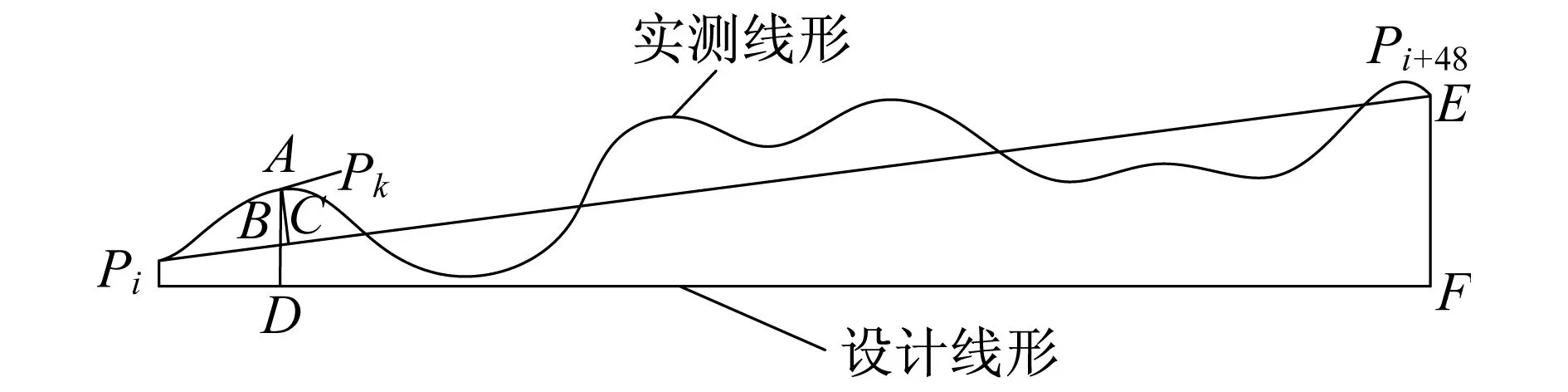
图5 弦长为48个轨枕间距的各检测点正矢值偏差计算示意图
设轨道几何形位检测点P(xi,yi,zi)为基线长为48个轨枕间距弦长的拉弦起点,则检测点P(xi+48,yi+48,zi+48)为拉弦终点,点P(xk,yk,zk)(i、k表示测点号,i≤k≤i+48)中的yk为各检测点平面的绝对坐标,zk为各检测点高程的绝对坐标。其中,yk为检测点到设计线形的横向距离,zk为检测点到设计线形的竖向距离。由文献[8]可得各检测点中波不平顺高低和轨向的正矢值偏差为:
(6)
测点Pi与测点Pi+8正矢值的偏差值为:
(7)
同理,可采用类似中波不平顺的计算方法计算基线长为480个轨枕间距弦长的轨道长波高低和轨向不平顺。其计算式为:
(8)
1.4 轨底坡计算模型
轨底坡(见图6)是轨底与轨道平面之间形成的横向坡度,是轮轨关系中轨道受力计算和轨道部件设计的一项重要参数。
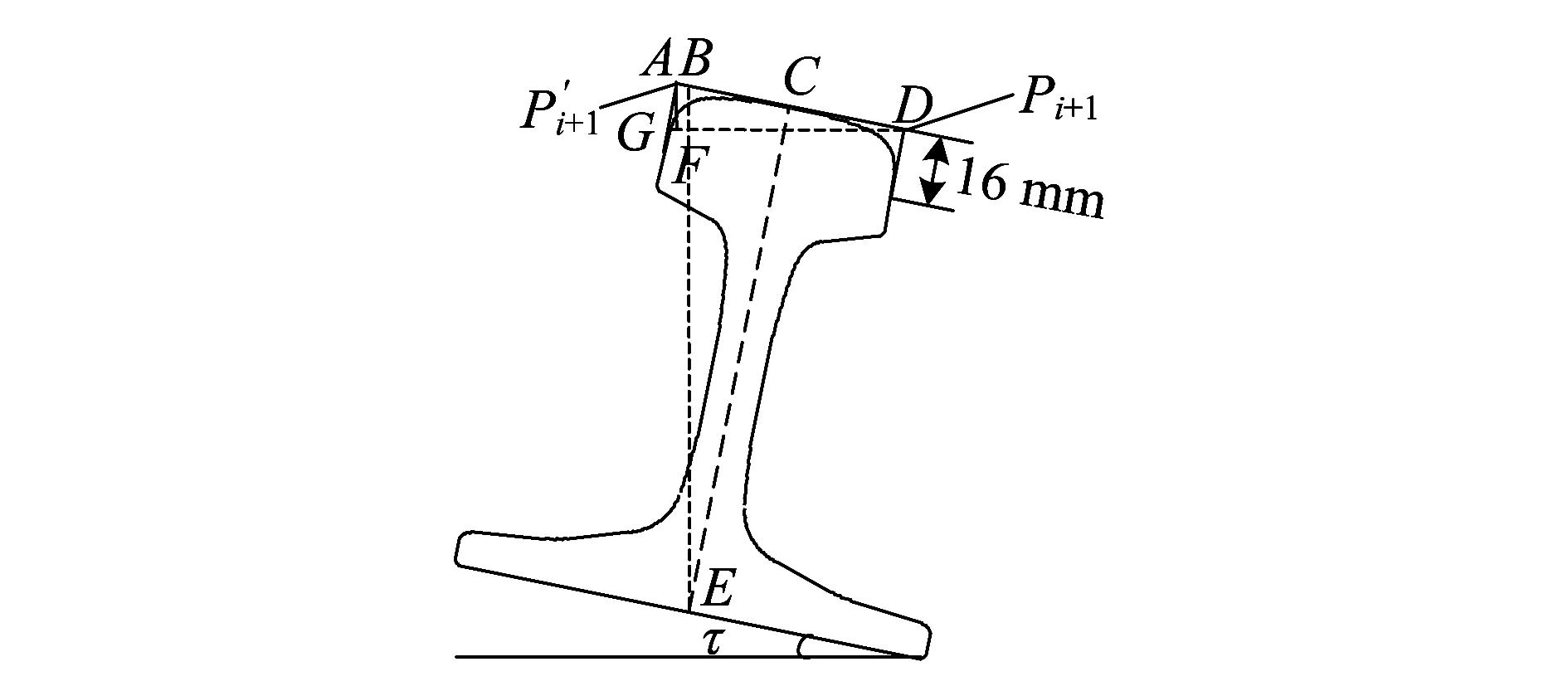
图6 轨底坡测量示意图
由图6可得轨底坡τ与检测点三维坐标的几何关系为:

(9)
2 测量试验与验证
为确保三维坐标测量轨道几何形位具有高精度性,本文采用高精度Leica AT401激光跟踪测量系统对所提出的轨道几何形位计算模型进行了试验。文献[9]对激光跟踪测量的实际精度进行了评定,激光跟踪测量轨道控制点高差精度为0.07 mm,且精度较均匀,满足无砟轨道几何形位测量精度的要求。
对20个检测点三维坐标数据进行采集,作为试验区段样本。根据提供的CPⅢ控制点已知参数,应用式(1)~(9)计算轨道几何形位参数,得到无砟轨道几何形位状态。表1为三维坐标测量无砟轨道几何形位的检测数据。
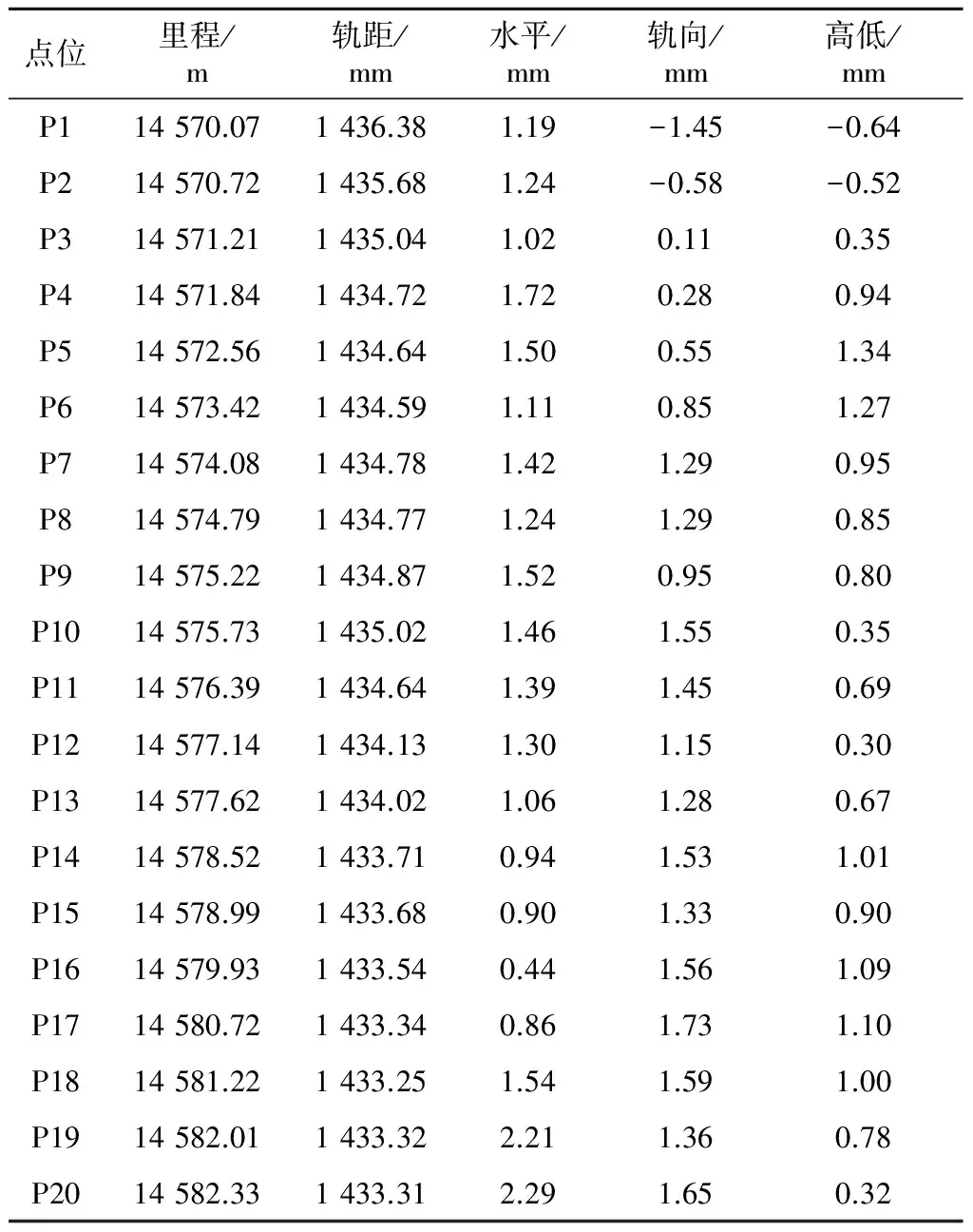
表1 轨道几何形位检测数据表
由表1可知,利用本文提出的测量方法可有效、准确计算出轨道几何形位参数。由于所采用的测量方法已满足无砟轨道几何形位的测量精度指标,因此,可确保三维坐标测量方法在无砟轨道几何形位检测中起到良好的作用。
3 结语
本文推导了轨道几何形位三维坐标计算模型,通过与激光跟踪测量技术相结合,实现以三维坐标测量方法检测轨道几何形位,并通过试验验证了该方法具有高精度以及可行性。三维坐标测量在满足轨道形位与大地坐标结合的同时,能够满足无砟轨道检测的高精度要求,为地铁及高速铁路无砟轨道几何形位检测提供了新的测量技术。
[1] 赵景民.无砟轨道施工测量与检测技术[M].北京:人民交通出版社,2011.
[2] 郝亚东,赵杰,樊廷春.基于GRP 1000的无砟轨道精调测量研究[J].测绘通报,2013(4):52-55.
[3] 杨成宽.GEDO CE轨道检测系统在无砟轨道施工测量中的应用[J].铁道工程学报,2009(3):57-61.
[4] 陈强,刘丽瑶,杨莹辉,等.基于双向近景摄影测量检测轨道平顺度的计算模型[J].铁道学报,2012,34(12):83-89.
[5] 高亮.轨道工程[M].北京:中国铁道出版社,2010.
[6] 安国栋.高速铁路精密工程测量技术标准的研究与应用[J].铁道学报,2010,32(2):98-104.
[7] 中华人民共和国铁道部.高速铁路工程测量规范:TB 10601—2009[S].北京:中国铁道出版社,2009.
[8] 金顺喜,王平,陈嵘.无砟轨道高低和方向不平顺计算方法研究[J].铁道学报,2012,34(5):81-85.
[9] 何越磊,黎桂,李再帏.基于激光跟踪测量的火箭橇轨道精测技术分析[J].郑州大学学报(工学版),2014,35(4):36-40.
Track Geometry Determination Model Based on 3D Coordinate Measurement
LI Gui, HE Yuelei
improve the accuracy and efficiency of ballastless track geometry fine tuning based on CPⅢ, a 3D coordinate measurement is presented for static detection of track geometry. The 3D coordinate measurement is carried out by the shape and position detection points on track geometry, and the track control network CPⅢ is taken as the measurement reference point. Then, the 3D geometric relationship of track geometry and the detection points are used to establish the computational model of 3D coordinate measurement track geometry. The testing results in track geometry measurement show that the 3D coordinate measurement can effectively detect the track geometry, the measurement accuracy can meet the requirements of precise indicators for ballastless track geometry.
metro; track geometry; 3D coordinate measurement; calculation model
*上海市科学技术委员会地方院校能力建设项目(14110501300);上海市研究生教育创新计划学位点引导布局与建设 培育项目(13sc002)
U 213.2+13
10.16037/j.1007-869x.2017.01.004
2015-03-08)
