局域共振型瓣状声学超材料带隙特性研究

陈 琳，吴卫国，周 榕

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

局域共振型瓣状声学超材料带隙特性研究

陈 琳，吴卫国，周 榕

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

针对现有研究中声学超材料完全带隙和相对带隙较窄的问题，设计了一种局域共振机理的瓣型声学超材料，运用有限元计算和仿真方法研究了该薄膜型声学超材料的能带特性及其振型特性，研究表明瓣型声学超材料的带隙宽度是无瓣型声学超材料带隙宽度的16倍，其相对带隙可达60%。

声学超材料；局域共振；完全带隙

声学超材料是由尺寸远小于作用波长的结构单元构成、并且有着奇异的反常规效应的人工结构[1]。2000年，刘正猷等人首次提出了局域共振机理[2]，实现了毫米级结构对大波长低频声波的有效控制。2004年王刚等人[3]设计的二维二组元声学超材料，首次提出了二维二组元声学超材料可以产生带隙的观点。沈平和杨志宇[4]研究了一种暗声学超材料实现了比布拉格散射机制频率低两个数量级的带隙。王刚[5]等人发明的局域共振型超材料可以达到带隙频率可调谐的目的。吴九汇[6]课题组研究了一种轻质二组元软性薄层局域共振声学超材料，这种超材料不仅能在500 Hz以下的低频打开完全带隙，而且能在频率低于100 Hz的超低频段打开垂向带隙。M. Badreddine和Mourad Oudich设计的超材料结构[7]约在3 kHz的频段产生了完全带隙。Osama R. 和Mahmoud 研究的一种类似跳板的声学超材料模型[8]可以产生较宽的亚波长带隙，并且其相对带隙也达到了55%。张思文和吴九汇等人提出的一种螺旋形结构能够在200 Hz以下的低频段打开方向带隙[9]。侯志林、马嘉宏和Badreddine M[10]等人研究的三维四组元结构能在76～311 Hz的频率范围内打开方向带隙，并且在频率120 Hz附近出现平带。

以上结构在一定频率范围内都可以产生禁带，但是有些完全带隙较窄[11-12]，有些带隙处于1 kHz中高频段[11,13]，有些禁带的产生并不是由单一元胞组成的单层结构实现的，而是通过多层结构堆叠或是改变胞元组成元素从而形成复合胞元达到较宽带隙的。本文设计了一种瓣型超材料微结构，并对其带隙特性进行了详细研究。

1 模型的建立

研究模型如图1所示，图1(a)是单瓣超材料元胞的模型，由半球图1(c)、“瓣”图1(d)、薄膜图1(e)、栅格支架图1(f)4部分组成。元胞为隔声装置中阻隔低频噪声的最小单元，图1(b)是不含瓣形结构的元胞；图1(g)是元胞阵列后的结构；图1(h)是阵列后的背面结构图。其中，栅格支架由正方形格子沿x方向和y方向周期性延拓而成，起着固定支撑的作用。中间的弹性薄膜相当于“弹簧-质量”系统中的弹簧，半球和“瓣”相当于质量块。

图1 瓣型声学超材料模型

2 数值计算及分析

由于该声学超材料是周期性的，本文首先计算了一个元胞的特征频率及带隙特性。所研究元胞结构中粘贴于弹性薄膜上的半球是金属钨，弹性薄膜是硅橡胶，刚性支架是硬质塑料。材料参数：硅胶密度ρ=1 300 kg/m3；弹性模量E=0.117 5 MPa；泊松比ν=0.469；塑料密度ρ=119 0 kg/m3；弹性模量E=2.2 GPa；泊松比ν=0.375；钨密度ρ=17 800 kg/m3；弹性模量E=360 GPa；泊松比ν=0.27。

2.1 能带结构计算

网格划分中采用系统默认的自由剖分四面体网格，而在硅橡胶所在域内自定义较细网格，在其他域内设置标准网格。如图2所示为本文研究的单瓣元胞的网格划分示意图，端点单元数为43，边单元数为401，边界单元数为5 021，单元数为9 957，自由网络时间为0.26 s。

图2 单瓣元胞网格划分示意图

计算中单瓣结构的元胞尺寸为b= 0.06a，R= 0.34a，h=0.1a，t=0.075a，e=0.025a，其中a=10 mm。无瓣结构几何尺寸与单瓣结构一样。元胞四周的边界均设置为Bloch-Floquet周期性边界条件，其他边界为自由边界，边界条件以两个同方向的面为一组进行施加，没有先后顺序之分。为了实现参数化建模，计算时可以扫略整个不可约布里渊区的高代表性边界Γ-X-M-Γ，通过COMSOL MULTIPHYSICS 4.3求解特征值后将特征值数据导入到Matlab中，计算可得到能带结构。此方法可以根据计算结果要求方便调整模型的尺寸，得到不同尺寸下超材料的能带结构。研究中计算了有“瓣”模型和无“瓣”模型[6]的能带结构，分别如图3(a) 和图3(b)所示，图3(a)中区域(1)是包括弯曲波[12]带隙在内的第一条带隙；第二条完全带隙用以(2)标注的区域表示，第二完全带隙的上边界是“平带”[11]；第三完全带隙是最宽的带隙，用区域 (3)标注，它的下边界是第二完全带隙的上边界。从能带图中可看出在相同尺寸相同材料下有“瓣”和无“瓣”元胞带隙特性相差很大，对比图3(a)和图3(b)可知有“瓣”模型产生的完全带隙个数和带宽都比无“瓣”模型要优越，有“瓣”模型可以产生3条完全带隙，而无“瓣”模型只产生很窄的一条完全带隙。由能带图可计算出瓣型结构产生的带隙宽度是无“瓣”模型的16倍([(305-140)+(92-76)]/(57-46)=16.4)，并且在400 Hz以下有3条完全带隙，带隙宽度达254 Hz，占作用总频率的65%，相对带隙(Δf/fc)达到60%。

图3 有“瓣”和无“瓣”元胞的能带图

2.2 结构模态分析

为了深入了解声学超材料带隙的产生机理，对结构元胞进行模态分析。图4所示7张图分别为图3(a)所示能带图中七条谱线A,B,C,D,E,F,G对应固有频率在M点的振动模态图。从图4(a)可以看出，元胞的第1种振动是在z方向的平动，能量主要集中在半球、瓣、弹性薄膜上。结构的第2、第3种振动形式都是在x-y平面内的转动，能量主要集中在转动轴的两侧。第4种振动是元胞沿x轴和y轴的对角线转动。这种结构的第4和第5种振动形式基本一样，都是沿y轴和沿x轴的平动，势能主要储存于瓣形结构和弹性薄膜里。第6种振动形式是在x-y平面内以z轴为转动轴的转动形式，这种形式的振动决定了能带结构中第6条谱线的形状是平直的“平带”[11]。第7种振动只有瓣的轻微振动，半球和弹性薄膜都保持静止，能量主要集中于瓣形结构中。

图4 单瓣元胞的模态

2.3 微结构几何参数对带隙特性的影响

影响声学超材料带隙特性的几何参数有多种，本文主要研究半球半径、弹性薄膜厚度、晶格常数、瓣的数量对3个带隙上下边界的影响规律。

(1)质量块半径对带隙特性的影响。

元胞中半球的振动是局域共振形成的重要因素，所以半球的质量对局域共振有较大影响。在保证其他几何参数a=10 mm，b= 0.6 mm，h=1 mm，t=0. 75 mm，e=0. 25 mm不变的前提下改变半球半径R的大小来研究半球半径对超材料带隙特性的影响。图5所示为半球半径为2.8 mm，3.2 mm时的能带结构图。

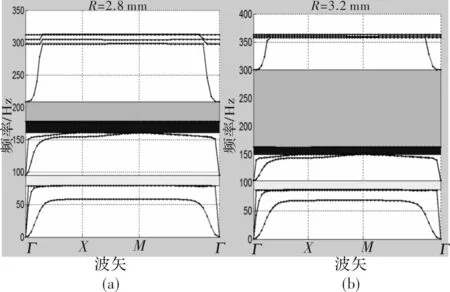
图5 半球半径为2.8 mm和3.2 mm时的能带图

从图5中不同半球半径下元胞能带结构的带隙边界可以看出，半球半径的大小对第一完全带隙的位置和宽度几基本有影响。但是第三完全带隙对半球半径的变化比较敏感，随着半球半径的增大第三完全带隙的宽度和中心频率均增大。图中蓝色区域所表示的第二完全带隙随着半球半径的变化而变化缓慢。元胞带隙特性随半球半径大小的变化具体规律如图6所示。

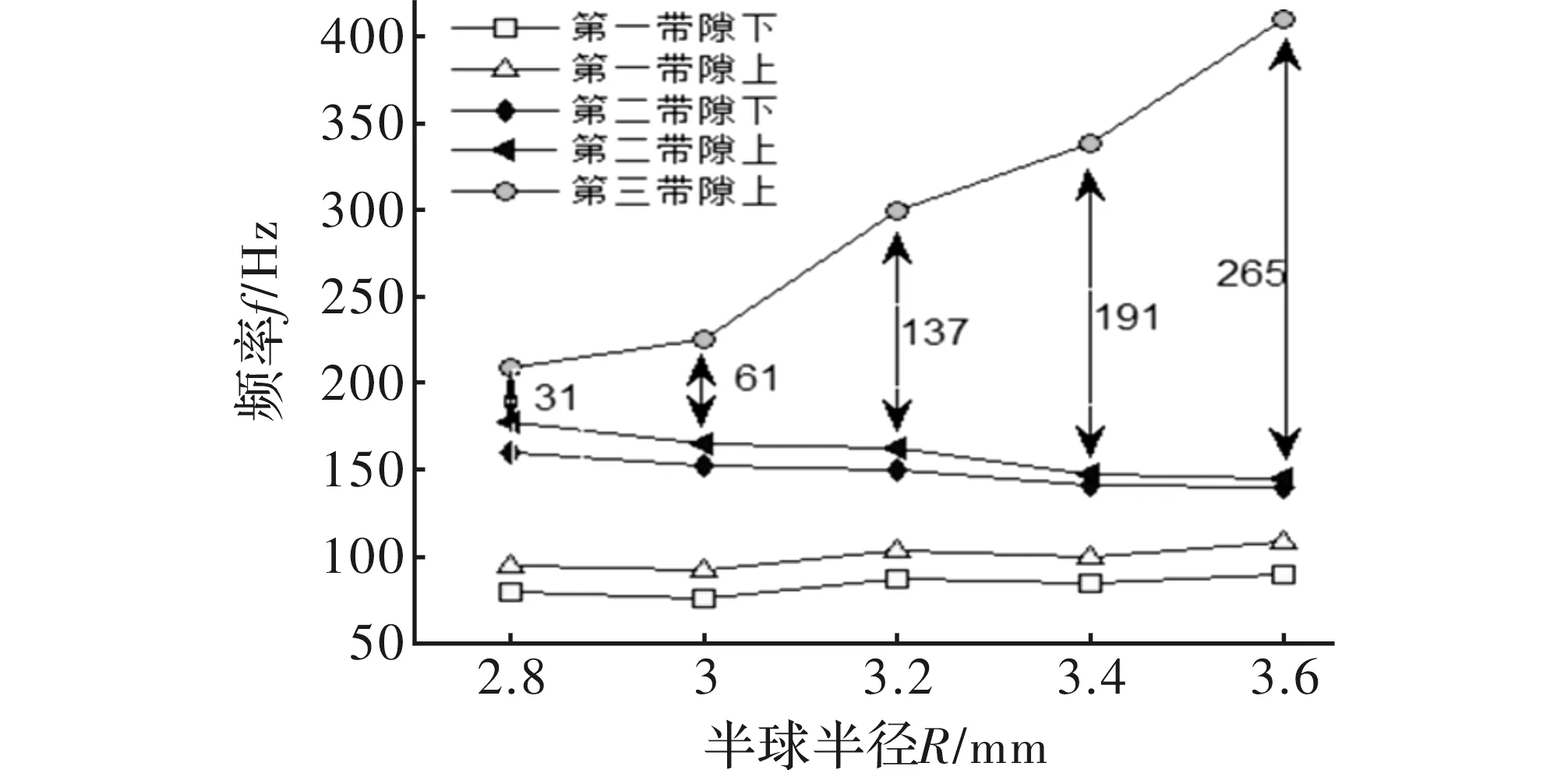
图6 带隙边界随半球半径变化的规律图

(2)薄膜厚度对带隙特性的影响。

在元胞局域共振中起到弹簧作用的就是硅橡胶弹性薄膜，半球在弹性薄膜的作用下发生局域共振。弹性薄膜的厚度影响了弹性薄膜的弹性性能，所以弹性薄膜的厚度对带隙特性有很大的影响。研究中当a=10 mm，R=3.0 mm，h=1 mm，t=0. 75 mm，e= 0. 25 mm，保持不变，弹性薄膜厚度b取0.4 mm，0.5 mm，0.6 mm，0.7 mm时计算元胞的能带结构，从带隙上下边界值得到如图7所示的规律图。

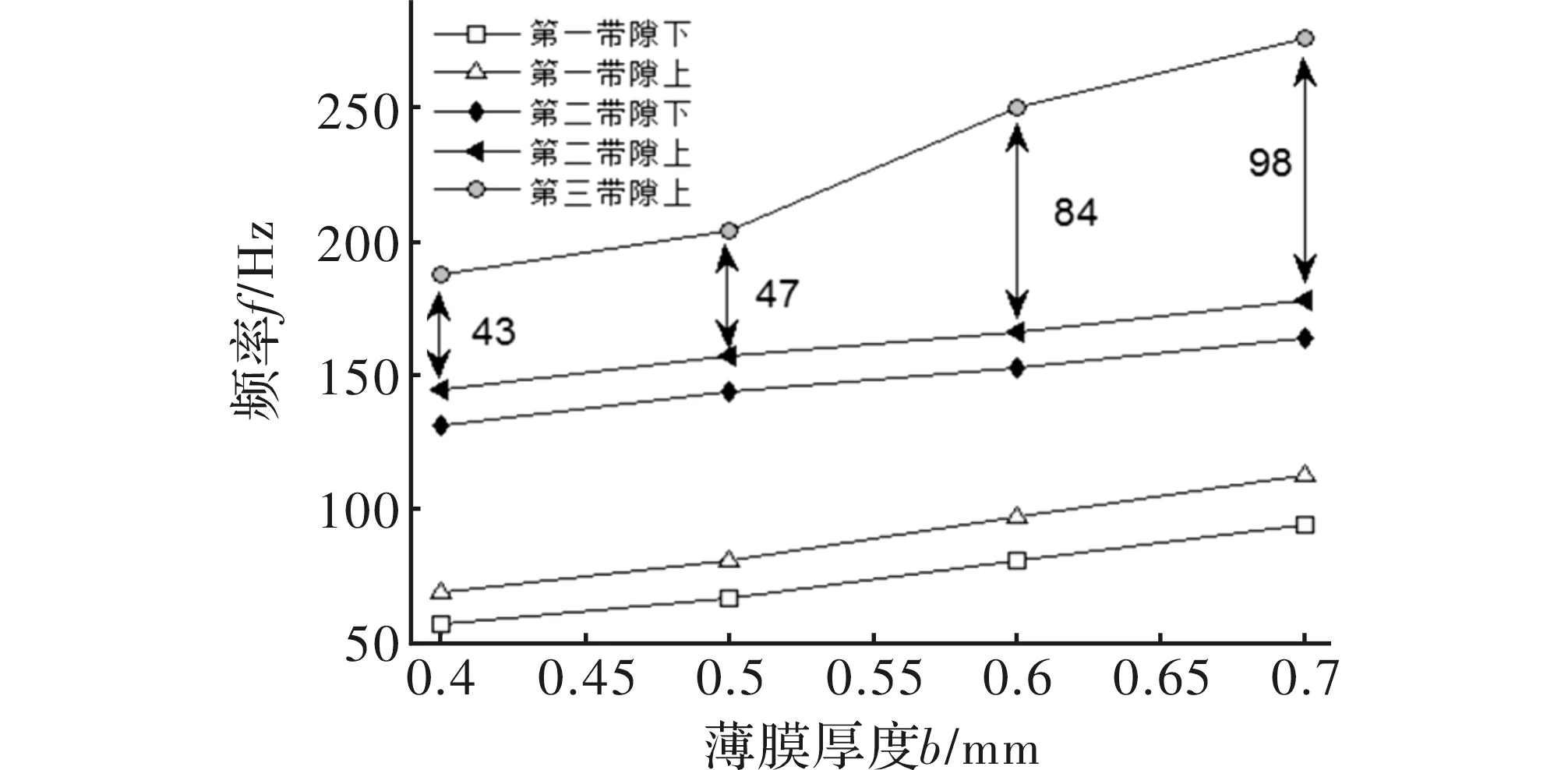
图7 带隙边界随薄膜厚度变化的规律图

从图7中可以看出随着弹性薄膜厚度的增大，第二、三完全带隙的宽度基本保持不变，但其中心频率逐渐向高频移动。当薄膜厚度b=0.4 mm时，元胞第三完全带隙宽度为43 Hz，当b增大到0.7 mm时，第三完全带隙的宽度达到98 Hz。所以，改变弹性薄膜厚度能提高元胞总的带隙宽度，因为元胞第三完全带隙的宽度占总的带隙宽度比例最大。

(3)晶格常数对带隙特性的影响。

声学超材料中影响带隙特性的影响因素中晶格常数的影响是比较重要的影响因素。当R=3.4 mm，h=1 mm，t= 0. 75 mm，e= 0. 25 mm，b=0.6 mm，晶格常数a取9 mm，10 mm，11 mm，12 mm，13 mm，14 mm时得出晶格常数对带隙特性的影响规律如图8所示。

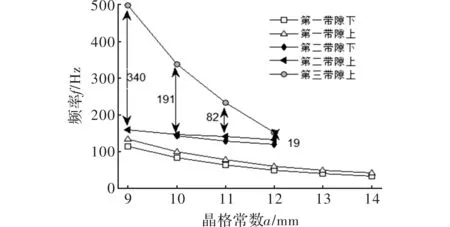
图8 带隙边界随晶格常数变化的规律图

从图8中看到晶格常数对带隙特性具有较大的影响，晶格常数的大小不仅能影响带隙的宽度和位置，还可以影响带隙的数量。出当晶格常数a=9 mm时，第三完全带隙宽度达到最大值340 Hz，能带结构中不存在第二完全带隙。当晶格常数a=10 mm时，第二带隙出现，但比较窄，第三完全带隙的宽度迅速降低为191 Hz。晶格常数的增大使得第一完全带隙的中心频率逐渐向低频靠近，但是宽度基本不随晶格常数的改变而改变。当晶格常数>12 mm时，第二、三完全带隙消失，只有第一完全带隙。

(4)瓣的数量对带隙特性的影响。

瓣型声学超材料的带隙之所以比其他研究模型具有优越性主要是因为模型中的“瓣”，瓣的数量势必会影响模型的带隙特性。如图9所示，研究中将一个瓣形结构划分为多个瓣状结构。为了研究瓣的数量对带隙的影响规律，取晶格常数a=10 mm，R=3.2 mm，h=1 mm，t=0. 75 mm，e= 0. 25 mm，b=0.6 mm，瓣的数量分别为1、4、6、8、10、12，对这些模型进行能带结构计算和模态分析。

图9 含瓣数量为1/4/6/8/10/12的元胞结构示意图

图10 瓣的数量变化对带隙特性的影响

从瓣的数量对各个完全带隙上下边界的影响规律图10所示，随着瓣数量的增多，第一、二完全带隙的宽度和中心频率的位置几乎不变，第三完全带隙的上边界随着瓣数量的增多而向低频偏移，最终使得第三完全带隙的宽度减小。当瓣的数量为1时(一个瓣就相当于一个圈形结构)，第三完全带隙宽度为113 Hz，第三完全带隙的宽度变得越小，当瓣数为12时，第三完全带隙宽度减小到瓣数为1时的1/2。

考虑到瓣形结构数量越多，模型的设计和加工难度也会加大，还有一个重要原因就是瓣形结构的数量越多越不利于宽带隙的形成，所以在今后的模型设计中不需要考虑多瓣结构，仅需要简单设计一个圈形结构就可以满足带隙要求了。其次，含一个瓣形结构的模型在研究模型几何参数变化时具有便于改变参数，计算收敛快等特点。

3 结束语

本文设计了一种基于局域共振(LR)机理的瓣型结构的声学超材料，研究表明该薄膜型声学超材料比无瓣型声学超材料带隙更宽，并且仅用单层结构同种元胞组合就可以在一定频率下形成较宽的多个完全带隙，而不需要通过不同种元胞组合或是多层结构的复合而达到一定带隙特性。从结构振动和能量聚集的角度解释了局域共振机理。各种为振动形式都是框架保持不动，其他部件不同程度的振动，从而实现了局域共振。结构几何参数中晶格常数，半球半径，薄膜厚度对带隙影响最明显。晶格常数越大，总的完全带隙宽度越小，弹性薄膜厚度在一定范围内与完全带隙宽度正相关，半球半径越大，第三完全带隙越大，总的带隙宽度也越大，但是半球半径必须要满足晶格常数的限定而不能随意变大。

[1] 梅军,马冠聪,杨昱,等.暗声学超材料研究[J].物理，2012, 41(7):425-433.

[2] Fung K H, Liu Z, Chan C T. Transmission properties of locally resonant sonic materials with finite slab thickness[J]. Zeitschrift Für Kristallographie,2005,220(220):871-876.

[3] Gang W, Xisen W, Jihong W, et al. Two-dimensional locally resonant phononic crystals with binary structures[J]. Physical Review Letters, 2004, 93(15):9587-9602.

[4] 沈平,杨志,温维佳,等. 声能吸收超材料，中国：CN 103137118A[P].2013-06-13.

[5] 吴健,王刚,白晓春,等. 一种轻质低频宽带薄膜超材料隔声装置，中国:CN103594080A[P]. 2014-04-12.

[6] 吴九汇,马富银,张思文,等，一种轻质二组元软性薄层局域共振声学超材料结构，中国:CN103996396A[P]. 2014-06-22.

[7] Assouar M B, Oudich M. Enlargement of a locally resonant sonic band gap by using double-sides stubbed phononic plates[J].Applied Physics Letters,2012,100(12):123506-123506-4.

[8] Bilal O R, Hussein M I.Trampoline metamaterial: Local resonance enhancement by springboards[J].Applied Physics Letters,2013,103(11):111901-111901-4.

[9] Zhang S, Wu J H, Hu Z. Low-frequency locally resonant band-gaps in phononic crystal plates with periodic spiral resonators[J].Journal of Applied Physics,2013(113):163511-163511-8.

[10] Ma J,Hou Z,Assouar B M.Opening a large full phononic band gap in thin elastic plate with resonant units[J].Journal of Applied Physics, 2014, 115(9):093508-093508-5.

[11] Oudich M, Li Y,Assouar B M, et al. A sonic band gap based on the locally resonant phononic plates with stubs[J].New Journal of Physics,2010,12(2):201-206.

[12] Ma F, Wu J H, Huang M, et al.A purely flexible lightweight membrane-type acoustic metamaterial[J].Journal of Physics D Applied Physics,2015,48(17):175105-175111.

[13] Wang Y F, Wang Y S, Su X X. Large bandgaps of two-dimensional phononic crystals with cross-like holes[J].Journal of Applied Physics, 2011, 110(11):113520-113520-13.

[14] Yang Z, Dai H M,Chan N H,et al.Acoustic metamaterial panels for sound attenuation in the 50～1000 Hz regime[J].Applied Physics Letters,2010,96(4):041906-041906-3.

Study of Band Structure for Petal-shaped Acoustic Metamaterials

CHEN Lin, WU Weiguo, ZHOU Rong

(School of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China)

This paper proposes a petal-shaped acoustic metamaterial structure to solve the relatively narrow complete band gaps and relative band gaps of previous studies. This metamaterial is based on local resonance. The band structures and vibration characteristics of the unit are calculated and analyzed by numerical simulations based on the finite element method. It is suggested that whole width of complete band gaps for the petal-shaped unit is more than 16 times that of the unit without petals, and the relative band gap is up to 60%.

acoustic metamaterial; local resonance; complete band gap

2016- 04- 12

镇江市科技支撑基金资助项目(GY2013032)

陈琳(1988-)，女，硕士研究生。研究方向：声学超材料在低频噪声控制中的应用。吴卫国(1970-)，男，副教授。研究方向：噪声控制及复合材料力学。周榕(1991-)，女，硕士研究生。研究方向：声学超材料在噪声控制中的应用。

10.16180/j.cnki.issn1007-7820.2017.02.042

TB53

A

1007-7820(2017)02-161-05