不同目标函数的传热结构拓扑优化研究
2017-03-07丁晓红
魏 啸,丁晓红
(上海理工大学 机械工程学院,上海 200093)
不同目标函数的传热结构拓扑优化研究
魏 啸,丁晓红
(上海理工大学 机械工程学院,上海 200093)
针对复杂传热结构的设计,可使用拓扑优化设计方法。通过基于密度法和SIMP插值模型的传热结构拓扑优化,得出高导热材料的合理分布形态。研究了以算术平均温度最小化、单位面积内能最小化及平均温度梯度最小化为目标的传热结构拓扑优化问题。拓扑优化结果显示,高导热材料集中分布在热源和散热边界的最短路径上,该结果符合传热学基本理论。
传热结构;拓扑优化设计;密度法;SIMP插值模型
随着微电子元件高度集成化的快速发展,传统对电子元件进行的强制对流换热方式已无法达到散热要求,解决问题的有效途径是通过对高导热材料的合理布置,在普通导热材料表面形成高效散热通道,达到对热量的高效传导。
高导热材的合理布置,不仅可提高导热效率,还可减少导热材料的使用率,降低成本。传统散热通道结构的设计,一般通过传热学基本知识和工程实践经验来完成。这种方法难以实现复杂散热通道结构的设计。针对复杂散热通道的设计,可使用拓扑优化设计,得到高自由度的散热通道拓扑形态,再结合工程实际要求,对拓扑形态进行尺寸优化,进而得到最佳散热通道。
结构拓扑优化设计,一般以材料的分布为优化目标,在一定的设计域内寻求最优的分布形态。目前在工程中具有成熟理论的拓扑优化方法主要有:有密度法[1]、均匀化方法[2-3]及Level set方法[4-5]等。这些方法在传热结构拓扑优化中均有应用。如Sigmund[6]在传热结构设计中应用密度法,对较为简单的稳态热传导问题进行了研究。Iga[7]以均匀化理论为基础,建立了总势能为目标函数的传热结构拓扑优化数学模型,从而确定了最佳散热通道。Yamada[8-9]在Level set方法的基础上,建立了热扩散最大为目标的传热结构拓扑优化数学模型,对导热结构刚度最大化问题进行了研究。
本文依托多物理场分析软件COMSOL Multiphysics,结合密度法和SIMP(Solid Isotropic Material with Penalization Model)插值模型,对以算术平均温度最小化、单位面积内能最小化及平均温度梯度最小化为目标的传热结构拓扑优化问题进行了对比研究,从而得到较为合理的散热通道形态。
1 传热结构拓扑优化数学模型
1.1 二维热传导问题
本文以二维热传导问题为例,对传热结构拓扑优化问题进行研究。
如图1所示,Ωd为设计域,其内有生热率载荷Q。设计域Ωd边界上存在第一类边界条件和第二类边界条件。第一类边界ΓT,边界温度为T0。第二类边界Γq,热流密度为q。传热结构的拓扑优化问题可描述为:设计域Ωd为低导热材料,在区域Ωd上合理布置高导热材料,形成散热通道,从而将该区域内的热量传送到边界。
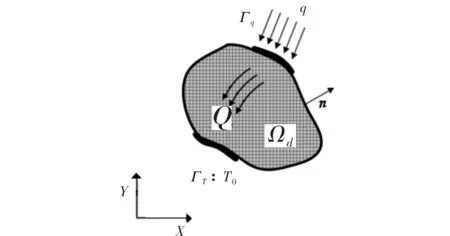
图1 二维热传导问题
1.2 优化数学模型建立
在基于密度法[1]的结构拓扑优化中,引入了伪密度的概念。伪密度并不是实际存在的物理量,而是假设的物理量。引入伪密度的目的是为了使数值求解过程更加方便直接。在各类物理场求解问题中,可将伪密度变量与实际的某一材料物理参数进行关联,从而在计算求解过程中建立伪密度和材料物理参数之间的函数关系。
通常在结构刚度优化中将伪密度变量与弹性模量通过插值的方式进行关联,两者之间的关系可以是线性的,也可是非线性的,如SIMP插值或RAMP(Rational Approximation of Material Properties)插值。将伪密度与材料物理参数进行关联,而不是直接用材料物理参数进行优化的优势就是,在数学模型表示方法上更加简洁直观,且通用性好,即可在不同的物理场模型中都能得到应用。
在传热结构拓扑优化问题中,在伪密度值与材料的热传导系数之间建立函数关系。常用的方法是采用SIMP插值模型,即固体各向同性材料惩罚函数模型。该插值模型是一种对中间变量具有惩罚效果的非线性插值模型。其方法是在导热系数的最大值和最小值之间插入一个指数函数。为保证插值模型具有较好的惩罚效果,通常伪密度值 限定在0和1之间。伪密度λ与热传导系数λ之间的函数关系为
λ=g(x)=(λmax-λmin)xp+λmin
(1)
式中,λmax、λmin分别是在传热结构优化中所用的导热系数的最大值和最小值。p是伪密度变量x的惩罚系数。当p=1时,插值模型对伪密度x不具有惩罚效果;当p>1时,插值模型对伪密度x具有惩罚效果,并随着p的增大惩罚效果也随之增大;当p<1时,插值模型对伪密度 具有增强效果,使得0~1内的伪密度 对材料热系数的影响力相近。
从而可将基于密度法的传热结构拓扑优化数学模型表示为
(2)
其中,x=(x1,x2,…,xn)T∈Rn,f:Rn→R1,x为优化设计变量,即伪密度变量;f(λ)为优化目标函数;g(x)为插值模型;vi为离散单元i的体积;v0是体积约束上限值。
2 传热结构拓扑优化目标函数
对于传热结构拓扑优化问题,诸多学者从不同目标函数出发,进行了不同的讨论。张晖[10]以温度最小化为设计目标,对设计域内温度分布的均匀性进行了研究。程雪涛[11]以散热弱度和温度方差为设计目标,讨论了温度梯度均匀化和温度场均匀化问题。工程中传热结构拓扑优化设计要求满足的条件主要有:最高温度最小、温度梯度分布均匀和温度场分布均匀等。目前,对传热结构拓扑优化设计问题的研究,多以散热弱度为设计目标[12]。这无法满足工程中对不同工况设计的要求。本文以算术平均温度最小化、单位面积内能最小化及平均温度梯度最小化为优化目标,对不同工况下的传热结构进行了优化设计,并对比其传热性能。
(1)算术平均温度最小化
(3)
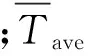
(2)单位面积内能最小化
(4)
其中,x为伪密度设计变量;fei(x)是设计域Ωd内的质量内能;|Ωd|是设计域Ωd的面积;Eei(x)是质量内能场函数。
(3)平均温度梯度最小化
(5)
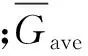
3 不同目标函数优化算例
建立如图3所示3种传热结构拓扑优化设计模型。设计域Ωd均100 mm×100 mm的正方形。设计域中心存在生热率为Q=3×107W/m3的中心热源。模型边界条件均为第一类边界条件,图2(a)和图2(b)分别为一边和四角散热边界模型,边界温度均为T0=0 ℃。低导热材料导热系数为λmin=1 W/(m·K)。

图2 传热结构拓扑优化模型
基于密度法的COMSOL传热结构拓扑优化其他设计参数[13]如表1所示。
分别以算术平均温度最小化、单位面积内能最小化及平均温度梯度最小化为优化目标,对以上2种工况进行优化设计。

表1 传热结构拓扑优化设计参数
3.1 一边散热边界优化结果
如图3~图5所示,拓扑形态一~形态三分别是以算术平均温度最小化、单位面积内能最小化以及平均温度梯度最小化为优化目标,拓扑优化产生的高导热材料分布形态。图4形态一可看出,在热源和散热边界之间产生了高导热材料主枝,主枝两侧对称分布了若干细小枝,高导热材料的分布较为分散,充满了设计域的左半部。图5形态二,除了在热源和散热边界之间产生了高导热材料主枝外,主枝两侧对称分布了两个分枝。高导热材料的分布较为集中。图6形态三只产生了热源和散热边界之间较粗的一条主枝,高导热材料分布集中,这在实际工程设计中较为合理。从以上3种形态可看出,高导热材料主要集中分布在热源和散热边界的最短路径上[14-15]。

图3 算术平均温度最小
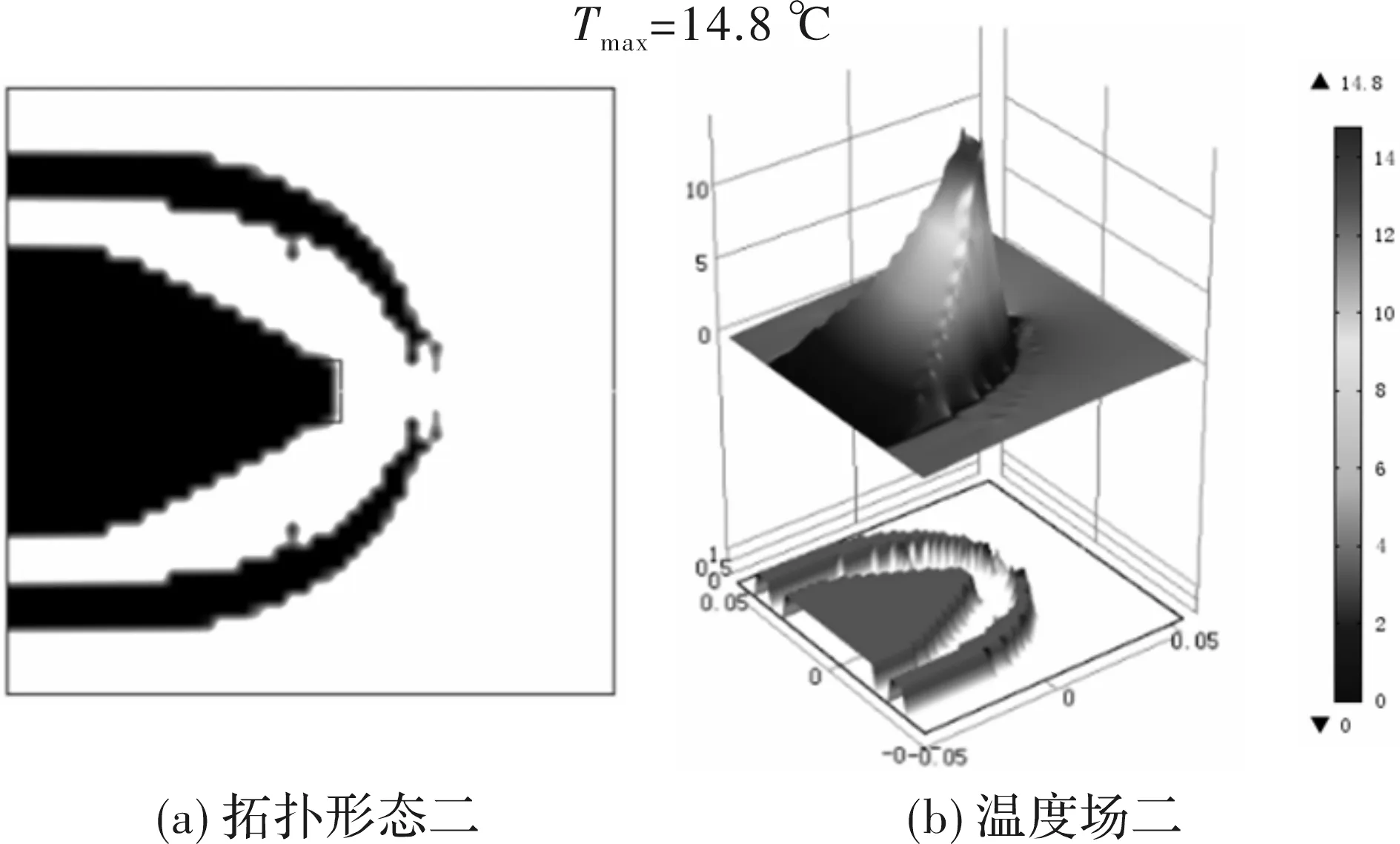
图4 单位面积内能最小

图5 平均温度梯度最小
图4~图6所示,温度场一~温度三分别是以算术平均温度最小化、单位面积内能最小化以及平均温度梯度最小化为优化目标,拓扑优化分析生产的温度场分布,可看出优化后温度场一~温度三最高温度分别为15.7 ℃、14.8 ℃、8.87 ℃,最高温度均出现在热源处。温度场一和温度场二的温度分布落差较大,温度场三温度分布较为平缓。
从以上拓扑形态和温度场分布分析可得出,以平均温度梯度最小为优化目标产生的高导热材料分布形态要比其他两种优化目标产生的优化结果更加合理。
3.2 四角散热边界优化结果
图6~图8所示为四角散热边界工况下的拓扑优化结果。从形态一~形态三可看出,该工况下,不同目标优化产生的高导热材料分布形态都为明显的“X”形。但以算术平均温度最小化和单位面积内能最小化为优化目标产生的形态,在设计域四边生产了细小分枝,而以平均温度梯度最小化为优化目标产生的形态,在设计域四边无细小分枝,而且主枝形态比前两个形态,更加清晰平滑。
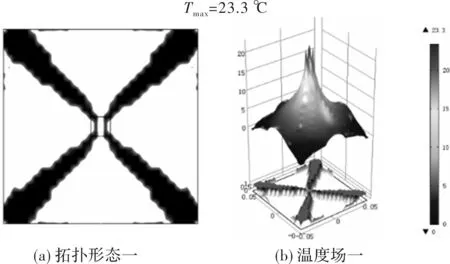
图6 算术平均温度最小
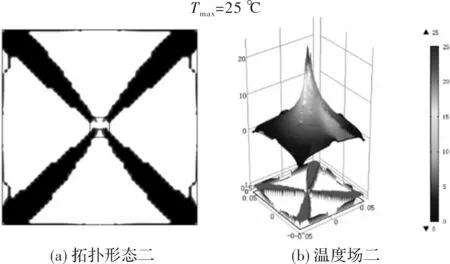
图7 单位面积内能最小
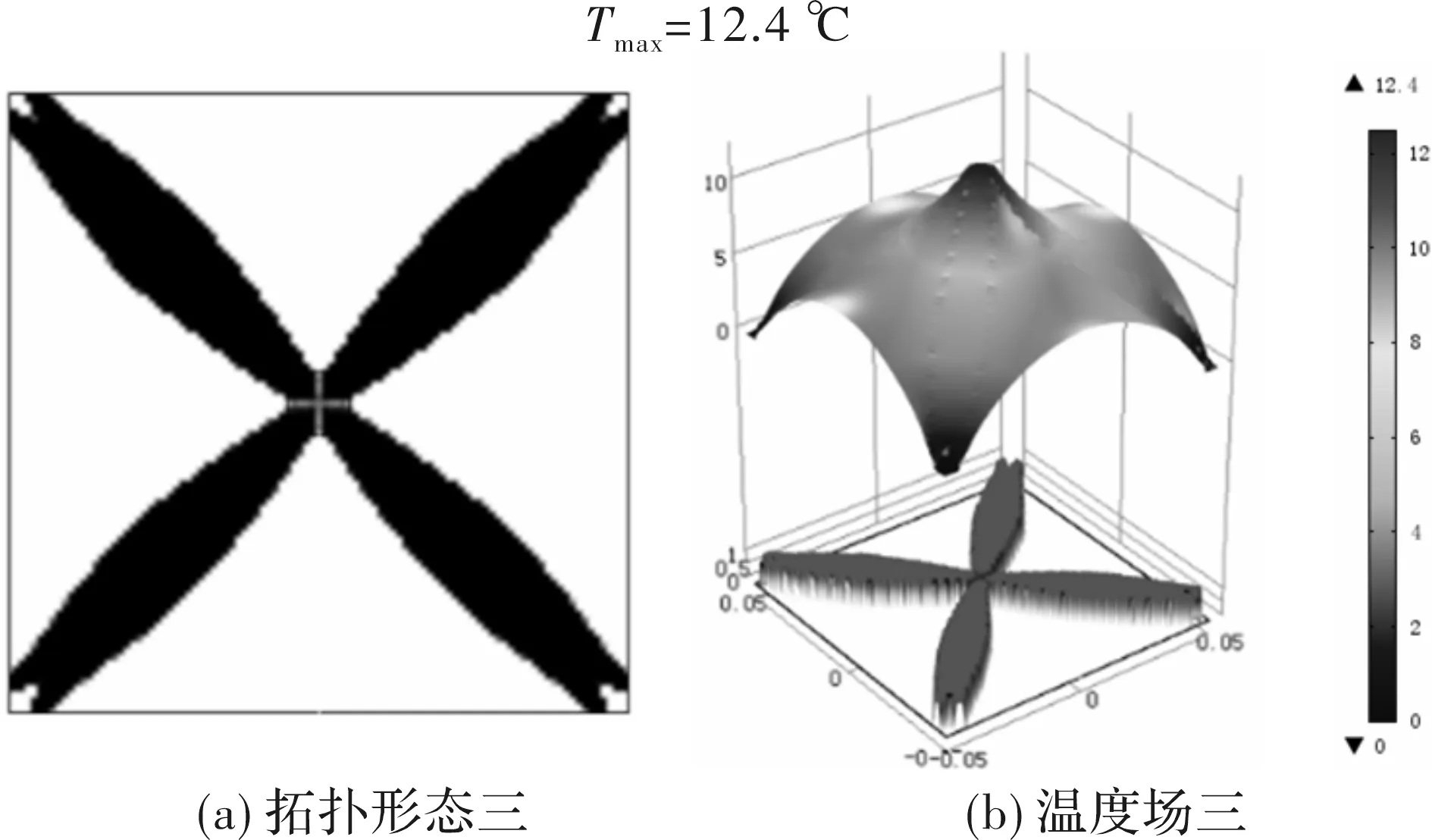
图8 平均温度梯度最小
优化后温度场一~温度三最高温度分别为23.3 ℃、25 ℃、12.4 ℃,最高温度均出现在热源处。温度场一和温度场二的温度分布落差较大,温度场三温度分布较为平缓。
在四角散热边界工况下,三类目标函数拓扑优化产生的高导热材料形态基本都为“X”形,但以平均温度梯度最小化为优化目标产生的形态更加清晰,无细小分枝产生,且温度场最高温度最低,该目标下,高导热材料分布更加合理。
4 算例结果对比
对以上不同工况下,采用不同目标函数拓扑优化产生的结果进行对比,如表2所示。
(1)通过对比可看出,以平均温度梯度最小为目标函数,拓扑优化产生的结果,在高导热材料形态分布和温度场分布两方面都要比其他两种目标函数下产生的结果好;
(2)不同目标函数优化产生的结果显示,一边散热工况下,温度场最高温度要比四角散热工况下最高温度底;
(3)四角散热边界工况,拓扑优化后,温度场最高温度比其它工况的高。这是因为散热边界与热源之间的路径比其他工况长的缘故;
(4)从两种工况拓扑优化产生的高导热材料分布形态可知,高导热材料主要集中分布在热源和散热边界的最短路径上。

表2 算例结果对比
5 结束语
通过基于密度法和SIMP插值模型的COMSOL传热结构拓扑优化,得出高导热材料的合理分布形态。研究了以算术平均温度最小化、单位面积内能最小化及平均温度梯度最小化为目标的传热结构拓扑优化问题。研究结果显示,相比其他两种优化目标产生的结果,以平均温度梯度最小化为目标,优化后的高导热材料分布形态更加清晰、无细小枝出现,符合实际工程要求。而且温度场最高温度也低于其他两种目标下的最高温度。其次,拓扑优化结果还显示,高导热材料集中分布在热源和散热边界的最短路径上,该结果符合传热学基本理论。
[1] Bendsøe M.Optimal shape design as a material distribution problem[J].Structural Optimization,1989,4(1):193-202.
[2] Bendsφe M,Kikuchi N.Generating optimal topologies in structuraldesign using a homogenizationmethod[J].Computer Methods in Applied Mechanics and Engineering,1988,71(2):197-224.
[3] Fujii D,Chen B,Kikuchi N.Composite material design of two-dimensional structures using the homogenization design method[J].International Journal for Numerical Methods in Engineering,2001,50(9):2031-2051.
[4] Wang M,Wang X,Guo D.A Level set method for structural topology optimization[J].Computer Methods in Applied Mechanics and Engineering,2003,192(1-2):227-246.
[5] Allaire G,Jouve F,Toader A. Structural optimization using sensitivity analysis and a level-set method[J].Journal of Computational Physics, 2004,194(1):363-393.
[6] Bendsøe M,Sigmund O.Topology optimization theory, methods, and applications[M].Germany:Springer Verlag,2003.
[7] Iga A,Nishiwaki S.Topology optimization for thermal problems based on assumed continuous approximation of material distributions[J].Transacions of the Japan Society of Mechanical Engineers,Series C,2007,733(73):2426-2433.
[8] Yamata T,Nishiwaki S.Level set-based topolog optimization method for thermal problems[J].Transacions of the Japan Society of Mechanical Engineers,Series C,2009,759(75): 2868-2876.
[9] Iga A ,Yamata T.Topogy optimization for coupled thermal and srtuctural problems U sing the level set merhod[J].Transacions of the Japan Society of Mechanical Engineers,Series C,2010,76(761):36-43.
[10] 张晖,刘书田,张雄.拓扑相关热载荷作用下稳态热传导结构拓扑优化[J].中国机械工程,2009(11):1339-1343.
[11] 程雪涛,徐向华,梁新刚.温度场与温度梯度场的均匀化[J].中国科学,2009,39(10):1730-1735.
[12] 乔赫廷,张永存,刘书田.散热结构拓扑优化目标函数的讨论[J].中国机械工程,2011(9):1112-1117.
[13] 崔天福,丁晓红,侯丽园.基于密度法的传热结构拓扑优化理论研究[J].上海理工大学学报,2014(6):548-555.
[14] 左孔天,陈立平,张云清,等.用拓扑优化方法进行热传导散热体的结构优化设计[J].机械工程学报,2005,41(4):13-16.
[15] 程新广,李志信.基于仿生优化的高效导热通道的构造[J].中国科学:E辑:技术科学,2003,33(3):251-256.
Topology Optimization of Transfer Structure for Different Objective Functions
WEI Xiao,DING Xiaohong
(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
The heat transfer structure is generally designed with basic knowledge of heat transfer theory and engineering practice and experience. Method of topology optimization design can be used in design of complex heat transfer structure. Reasonable arrangement form of high thermal conductivity material is found by heat transfer structure topology optimization design based on density method and SIMP interpolation model. Topology optimization problems of heat transfer structure are studied and the problems are usually for minimizing arithmetic mean temperature, internal energy of per unit area and average temperature gradient. Topology optimization results show that the high thermal conductivity material is distributed on the shortest path between the heat source and the thermal boundary, which accords with the basic theory of heat transfer.
heat transfer structure; topology optimization design; density method; SIMP interpolation model
2016- 04- 11
魏啸(1991-),男,硕士研究生。研究方向:结构分析与优化设计。丁晓红(1965-),女,博士,教授,博士生导师。研究方向:机械系统和结构现代设计理论。
10.16180/j.cnki.issn1007-7820.2017.02.041
TN304
A
1007-7820(2017)02-156-05
