基于表面肌电多尺度熵的递增负荷诱导肌肉疲劳评估

许全盛，李世明，季淑梅，翟佳丽

运动性肌肉疲劳是指运动引起的骨骼肌产生最大随意收缩力量或输出功率暂时性下降的生理现象[1]。表面肌电（surface electromyography，sEMG）是一种由众多骨骼肌纤维运动单位的电位在皮肤表面叠加而成的生物电信号，其中蕴含着丰富的肌肉系统生理病理信息，表面肌电信号分析与参数提取是评估肌肉疲劳重要手段[2-3]。研究[4-6]证实，骨骼肌静态收缩时产生的sEMG近似为平稳随机信号，肌肉疲劳程度与sEMG信号的平均频率、中值频率等频域参数基本呈负线性相关，而与肌电振幅、积分肌电等时域指标大致呈正线性相关。但在骨骼肌动态收缩时，由于电极位置、动作电位传导速度、肌力以及肌纤维长度等因素的变化大大增加了sEMG信号的了非平稳性和非线性[7]，如果再考虑sEMG振幅和频域参数对肌力和疲劳状态的双重依赖性[8]，通过sEMG信号的传统时域和频域参数来评价肌肉疲劳的可靠性大大降低。

非线性动力学和时频分析方法是非平稳信号处理的有力工具，时频分析无需信号的平稳性假设，能够获得信号在任意时刻和频率的二维能量分布即时频谱，进而计算出信号的瞬时平均频率和瞬时中值频率[9-12]。研究[12]表明，由时频分析所得瞬时频率参数比传统频域指参数能更客观的反映肌肉的动态疲劳程度，同时还能降低肌力因素对频域参数的影响。但时频分析仍然存在不足，首先是计算量远远大于传统频域分析；其次是在人体生理系统的高度非线性和混沌背景下，时频谱并不能完全表征信号特征。相比而言，非线性动力学参数的提取过程不需太大的计算量，也同样无需信号的平稳性假设，其中sEMG信号的复杂度是反映肌肉疲劳水平的一种常用的非线性指标[13-14]。根据生理系统的复杂性理论，健康生理系统比病态或衰老系统具有更高的复杂度，个体应对各种复杂和不利环境的适应调节能力更强，而生理系统的复杂度反映在心电、肌电和脑电等生理信号中[15-18]，如果把肌肉疲劳看成是一种“病态”，那么表面肌电信号的复杂度则反映了不同状态下的肌肉疲劳状况。近似熵（Approximate entropy，ApEn）及样本熵（Sample entropy，SampEn）作为最早用来评价生理系统的复杂度，至今仍不失为一种有效手段[19-21]，但由于局限在一个时间尺度，近似熵和样本熵均不能反映健康系统中内在的时域波动，而多尺度熵（Multi-scale entropy，MSE）是多个时间尺度上的样本熵测量，能够体现生理系统更完整的信息，在处理各类复杂条件下的生理信号时相比传统样本熵更有优势[22-23]。

考虑到日常生活和体育比赛中人的运动负荷大多是随时间变化的，而跑步、自行车、赛艇、游泳等许多项目需要骨骼肌做大量周期性的动态收缩，因此，对运动负荷随时间变化时肌肉周期性动态收缩这种复杂条件下产生的疲劳进行评估有着重要的现实意义。本文通过功率自行车试验，研究递增负荷诱发股四头肌疲劳过程中sEMG信号多尺度样本熵的变化规律，探讨利用sEMG信号的多尺度熵复杂度指标评估时变负荷下肌肉动态疲劳等级的可行性。

1 研究对象与方法

1.1 试验对象

挑选10名男性体育系本科生志愿者作为试验对象，年龄（20.7±1.3）岁，身高（1.73±0.03）m，体重（65.90±2.28）kg，受试者身体健康，均为右利手，无任何运动损伤史，试验前24 h未参与任何形式的剧烈运动，试验前签署知情同意，并由试验人员告知试验流程。

1.2 试验方法

受试者佩戴心率遥测表，在MONARK824型功率自行车上进行递增负荷蹬车试验，采用世界卫生组织推荐的踏车方案[12]：受试者先在零负荷下蹬车1 min以适应50 r/min的转速。初始负荷为50 W，蹬车每3 min后递增50 W直至200 W。本文定义1～4级负荷分别为50、100、150和200 W，每级负荷蹬车3 min，5级负荷则定义为4级负荷结束后到运动终止前的一段时间，采集1～5级负荷最后5 s的股直肌、股内侧肌、股外侧肌的sEMG信号。若受试者经反复鼓励仍不能按规定强度蹬车10 s以上，并且心率达到预期最大值（220-年龄），便认为肌肉已达极度疲劳，停止运动。作为一种标准试验范式，功率自行车蹬车试验诱导运动疲劳具有代表性，蹬车时下肢肌肉的周期性动态收缩是日常生活和体育项目中人体动作最基本的肌肉工作形式，而递增负荷的运动模式则可以使肌肉快速进入疲劳状态，试验流程统一规范，疲劳分析结果具有普适性。

1.3 表面肌电信号采集

采用中科院智能研究所开发的JE-TB0810八通道肌电采集系统采集受试者sEMG信号，电极片采用上海钧康医用设备有限公司产Ag/AgCI一次性使用圆形心电电极，直径2.5 cm；3个电极成等边三角形贴于待测肌肉上。为减少肌肉的交叉干扰，将电极贴放在肌肉肌腹沿肌纤维走向的方向上。电极贴放前分别用磨砂纸和医用酒精擦拭皮肤以减小电阻。肌电仪所有通道配备截止频率为10 Hz的一阶高通滤波器和截止频率为500 Hz的二阶巴特沃斯低通滤波器，采样频率为1 000 Hz。为降低数据传输线对受试者的影响以及防止电极受牵拉产生移动，试验时对数据传输线和电极片进行了捆绑。

功率自行车转速保持在50 r/min时曲柄转动周期为1.2 s，因此每级负荷最后5 s采集的原始sEMG信号大约包括4个收缩周期，每个周期股四头肌和股二头肌轮换做向心收缩，时间各为0.6 s左右。采集的股直肌、股内侧肌和股外侧肌的sEMG信号中振幅在零附近的部分对应股二头肌的收缩。利用Matlab2009a对采集的sEMG信号进行预处理，设计四阶巴特沃兹数字陷波器滤除50 Hz的工频干扰，将去除干扰后每位受试者的总共15段sEMG（5级负荷×3块肌肉）时间序列用于多尺度熵分析计算。

1.4 sEMG信号的多尺度熵计算

1.4.1 粗粒化过程

多尺度熵实际上是在多个离散时间尺度τ上计算的时间序列（信号）x（t）的样本熵[22-23]。令{xi}表示一个长度为N的sEMG时间序列，粗粒化后尺度为τ的sEMG时间序列变为，由下式给出：

1.4.2 样本熵计算 （1）对数据长度为Ns的时间序列{yτj}，重构m维相空间，其中的m维模板向量为：

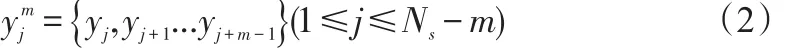
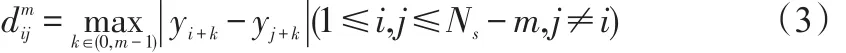
s的的个数表示以为中心，在窗口长度为m、设定容许偏差（阈值）为r的情形下，其余向量与的

（4）令m=m+1，重复步骤（1）至（3），用Um+1(r)表示小于r的概率

（5）样本熵定义为Um+1(r)与Um(r)之比的负对数：

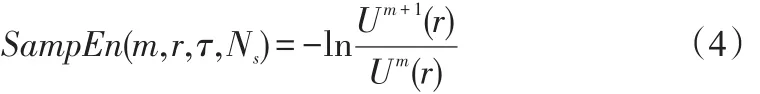
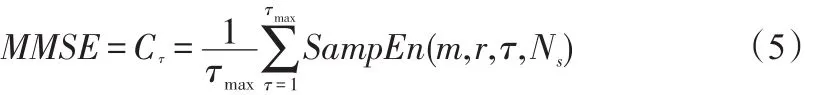
2 结果与讨论

2.1 时域波形分析

为便于波形观察，将功率自行车递增负荷试验采集到的每位受试者的股直肌、股内侧肌、股外侧肌1～5级负荷共5段sEMG信号整合成1段信号，形成3组25 s，每组25 000点的时间序列，如图1所示（以受试者张XX为例）。相邻负荷的sEMG数据用竖线隔开。由于功率自行车转速保持在50 r/min，转动周期为1.2 s，所以每级负荷运动最后5 s肌肉完成4次收缩，每个周期内大腿前群和后群肌轮换做向心收缩，时间各为0.6 s左右。从时域波形看，3块肌肉sEMG的振幅随负荷增长依次增大，其中1～2级负荷比较接近，而4～5级负荷sEMG幅值明显大于1～2级负荷。这跟1～2级负荷较轻，运动时间较短，大部分被试肌肉尚未达到疲劳状态有关。在本试验中，运动负荷增大迫使肌力增大，以保持功率自行车50 r/min的转速，而sEMG振幅对肌力和疲劳状态有双重依赖性[9]，因此，图1所示的时域波形幅度逐渐增大与负荷变化和疲劳产生都有关系，无法从时域波形上准确划分疲劳发生发展过程。

2.2 多尺度熵分析

分别计算每位受试者的股直肌、股内侧肌和股外侧肌1～5级负荷的sEMG信号多尺度熵，首先根据式（5）确定尺度为1所对应的时间序列（即粗粒化前的原始sEMG信号）的最优相空间维数m为2，容许误差r为0.15，再根据公式（1）～（4）计算各肌肉sEMG信号的多尺度熵，最大时间尺度选为30，将1～5级负荷的多尺度熵随尺度变化的曲线显示在1张图中，如图2所示。其中图a、c、e为受试者张XX的3块肌肉的计算结果，图b、d、f为所有被试在每个尺度上的多尺度熵平均值和方差。从图a、c、e可见张XX 3块肌肉的1～5级负荷多尺度熵曲线规律明显，表现为：多尺度熵曲线随负荷递增整体下移，1～5级负荷从上到下排列；各级负荷的多尺度熵一开始随尺度增加而增加，在尺度大于10左右时曲线逐渐平缓，相邻负荷多尺度熵曲线上下间隔拉开；负荷1和负荷2的多尺度熵在小尺度时很接近，而负荷4和负荷5在所有尺度上的数值都相对其他相邻负荷更接近。由图b、d、f可见，所有受试者整体上的表现与张XX类似，不同之处在于：负荷1和负荷2的多尺度熵曲线在尺度较小时存在交错和重叠，较难分开；股内侧肌负荷4和负荷5的多尺度熵曲线相对股直肌和股外侧肌更接近。

图1 1～5级负荷最后5 s的原始sEMG信号Figure1 Raw sEMG Signal Acquired During the Last 5 Seconds from Load 1 to Load 5

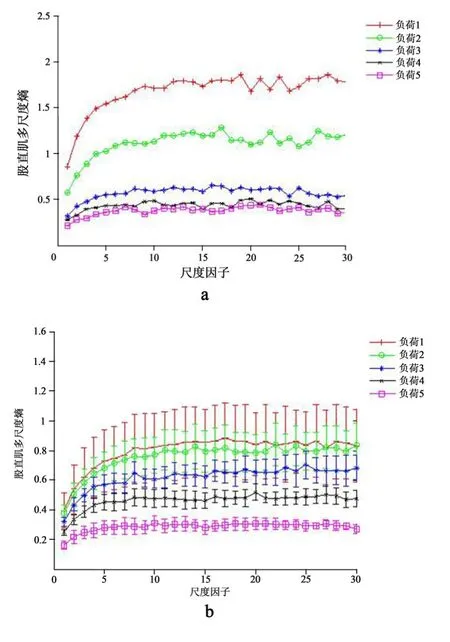
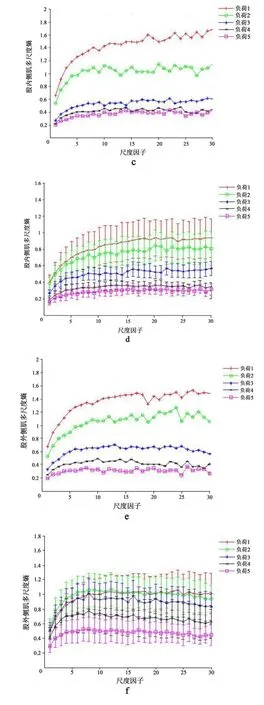
图2 1～5级负荷的sEMG信号的多尺度熵随尺度的变化Figure2 MSE of Load 1～5 Loads Computed by sEMG Signal at Different Scale Factors

众所周知，肌肉疲劳程度是一个随着负荷的增加和运动时间的延长而逐步发展的过程，即从未疲劳到轻度疲劳，再到中度疲劳，最后达到重度或极度疲劳状态。根据图2的分析可知，受试者功率自行车的试验结果存在一定的个体差异，不同肌肉在不同负荷下的疲劳发展过程也不尽相同，但同时又呈现出比较明显的共性规律，总体上可以认为：负荷1未产生疲劳，肌肉处于“健康”状态；负荷2处于疲劳前期或出现轻度疲劳，多尺度熵略有下降，肌肉工作在“亚健康”状态；负荷3肌肉开始出现疲劳，肌肉工作进入“病态”；负荷4肌肉处于中度疲劳；负荷5肌肉处于重度或极度疲劳状态，相当于“严重病态”。研究认为不同肌肉进入疲劳的时间和程度的差异取决于不同受试者在蹬车动作中的发力方式、发力程度和肌肉力量的基础水平有关。

2.3 复杂度分析

进一步观察图2可知，负荷1和负荷2的多尺度熵曲线在尺度较小时存在交错和重叠，特别在尺度1（对应传统样本熵）时，不能准确反映出疲劳随时间和负荷递增逐渐发展的事实。另外，各级负荷的多尺度熵曲线在尺度10至20已经能实现很好的分离，这意味着更大尺度的多尺度熵计算是不必要的，最大尺度的选择可以根据sEMG的数据长度决定。本文将所有尺度上的多尺度熵的平均值定义为评定肌肉疲劳等级的复杂度指标，即将图2中b、d、f得到所有受试者各级负荷下在所有尺度的样本熵平均值相加后再求一次平均，得到平均多尺度熵（Mean Multisacle Entropy，MSE），也就是多尺度复杂度（Cτ），将所有受试者在所有尺度的样本熵的方差相加后求平均值作为多尺度复杂度的方差。尺度为1时的传统样本熵和尺度1～30时的平均多尺度熵结果见表1。

为便于对比，将表1中各肌肉的平均多尺度熵和传统样本熵大小用柱状图并列显示于图3。其中图a、c、e分别为股直肌、股内侧肌和股外侧肌的平均多尺度熵和方差，b、d、f为传统样本熵及其方差。不难发现，平均多尺度熵比传统样本熵能更准确的区分肌肉疲劳随时间和负荷递增的发展历程，图a、c、e显示3块肌肉的多尺度熵水平随负荷递增而单调下降，其中股外侧肌负荷1和负荷2数值最为接近，但仍存在显著差异（P＜0.01）。而从图b看股直肌负荷1和负荷2的样本熵差别的显著性较低（P＜0.05），图d表明股内侧肌负荷1负荷2的样本熵不存在显著差别（P＞0.05），而图f则发生了交错，负荷1的样本熵低于负荷2，与疲劳发展的实际过程相违背。由以上分析可见，平均多尺度熵相比传统样本熵的优势在于不仅能反映肌肉疲劳的发展过程，而且能够区分相邻负荷间疲劳水平的微小差异。另外，从图a、c、e看出，股直肌和股外侧肌总体上相对股内侧肌在负荷5的平均多尺度熵远低于负荷4，反映出蹬车动作中3块肌肉肌肉的发力程度存在差别。

表1 功率自行车递增负荷运动sEMG信号的平均多尺度熵和传统样本熵值Table1 Comparison of MMSE and Sample Entropy of sEMG During Increasing Load Exercise on Cycle Ergometer

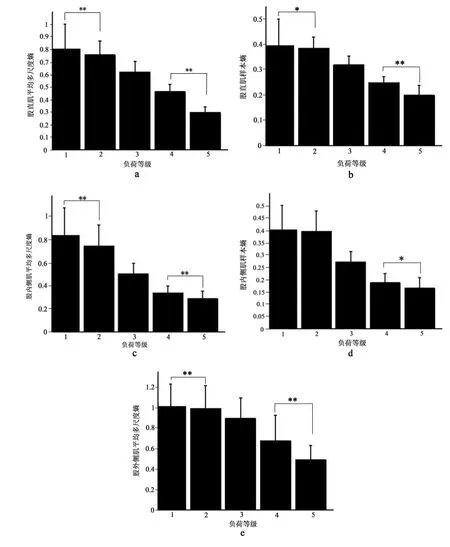
图3 尺度1～30的平均多尺度熵（a、c、e）和尺度为1时的传统样本熵（b、d、f）随负荷递增的变化Figure3 Comparison of MMSE Over Scale Factor 1～30 and Sample Entropy at Scale One

实际应用时，可以通过计算运动员sEMG信号平均多尺度熵相对运动开始时（非疲劳状态）的下降程度来估计相应肌肉的疲劳程度。因此，将表1中的平均多尺度熵用其最大值归一化，结果如表2所示，其中100%表示负荷等级为1的运动最开始阶段。根据本文功率自行车试验的实际过程和受试者的主观感受，疲劳感觉从负荷3末期开始出现，到负荷4疲劳逐渐加剧直至负荷5末期进入极度疲劳或力竭状态，从表2看，即当平均多尺度熵下降至运动开始时的70%～80%时，肌肉开始出现轻微疲劳，当下降至50%～70%时，肌肉进入中度疲劳状态，而下降至低于50%时，肌肉处于极度疲劳状态。

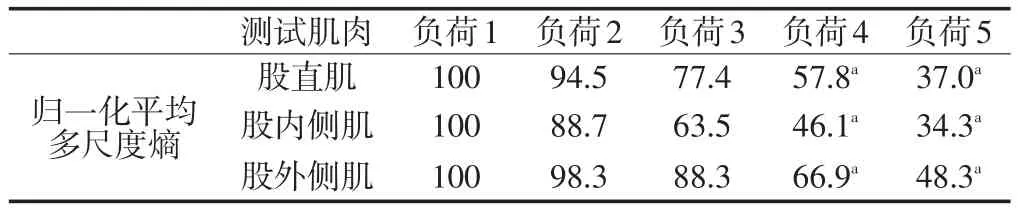
表2 不同负荷下sEMG信号的归一化平均多尺度熵/%Table2 Normalized MMSE of sEMG at Different Loads/%

综合以上分析，本文sEMG信号的多尺度熵分析结果从一个侧面较好与生理系统的复杂性理论相吻合，即病态系统的生理信息量降低表现为降低的复杂度或熵值。而传统样本熵不能准确反映病态系统的复杂度特征，这点与文献[22-23]的研究结果一致。本研究中，股四头肌疲劳随着时间推移和功率自行车负荷增加逐步产生和发展，递增负荷起到加速和加剧疲劳的作用，疲劳的出现意味着肌肉“病态”工作，神经-肌肉系统复杂度降低，中枢神经调节能力减弱，表现为sEMG信号的多尺度熵曲线下移。

本文通过表面肌电信号的多尺度熵分析对肌肉周期性动态收缩的疲劳进行评估，克服了肌肉在动态收缩时由于电极位置、动作电位传导速度、肌力以及肌纤维长度等因素的变化导致的sEMG信号的非平稳性和非线性。多尺度熵方法同样也适用于评估等动（等速）收缩和等长（静态）收缩，而当前大多数肌电分析软件普遍采用频谱分析手段和指标，必须基于肌电信号的平稳性和线性性假设，适合评估静态收缩和恒定的中等负荷以下的动态收缩疲劳，但在时变负荷和高强度动态收缩情形下，由于肌电信号的频谱指标与肌力因素（由负荷变化引起）和疲劳程度间的相互作用，传统肌电分析软件的使用具有相当的局限性。时频分析无须考虑信号的非平稳性，克服传统频谱分析的局限性，但时频分析的计算量远高于多尺度熵分析，在实际应用中其实时性要差一些。总之，多尺度熵方法在肌肉疲劳估计应用中更具优势，而肌电信号的平均多尺度熵更准确的反映了肌肉系统的复杂度，相比传统样本熵更适合作为评估时变负荷下肌肉动态疲劳的量化指标。

3 结论与建议

本文探讨了基于多尺度熵分析的递增负荷诱导肌肉动态疲劳的评估方法。10名受试者完成功率自行车1～5级负荷的蹬车试验，采集的股直肌、股内侧肌和股外侧肌的sEMG信号用于多尺度熵分析，发现sEMG信号的多尺度熵曲线随着负荷递增而整体下移，当尺度大于10时各级负荷多尺度熵曲线分离明显，从上往下按负荷递增顺序排列，与肌肉疲劳实际发展过程一致，可以认定负荷1至负荷5肌肉的工作状态依次处于未疲劳、轻度疲劳、中度疲劳、重度或极度疲劳状态；但尺度较小时相邻负荷多尺度熵曲线容易出现重叠和交错，尺度为1时最为严重，表明传统样本熵方法的局限性。

研究表明，多尺度熵分析能适应时变负荷下肌肉动态收缩时sEMG信号的高度非线性和非平稳性，能够获得与时频分析方法基本一致的肌肉动态疲劳的评估结果，但在算法复杂度和计算量方面显著低于时频分析，因此，建议在实际工作中将归一化平均多尺度熵作为评估时变负荷下肌肉动态疲劳状况的一个量化指标，即通过计算sEMG信号的平均多尺度熵相对运动开始时（非疲劳状态）的下降程度来估计相应肌肉的疲劳程度，当平均多尺度熵下降至运动开始时70%以下时，可以认为肌肉处于疲劳状态。

[1]李世明.运动技术诊断概论[M].北京：科学出版社，2014.

[2]曲峰.运动员表面肌电信号与分形[M].北京：北京体育大学出版社，2008.

[3]刘瑞东，陈小平.功能性力量训练对肌肉募集特征和身体素质的影响[J].上海体育学院学报，2016,40（5）：73-79.

[4]王健.静态负荷肌肉疲劳过程中肌肉功率谱转移特征[J].中国运动医学杂志，2001，20（2）：199-201.

[5]ADAM A，DELUCA C J.Firing rates of motor units in human vastus late⁃ralis muscle during fatiguing isometric contractions[J].Journal of Ap⁃plied Physiology，2005，99（1）：268-280.

[6]GONZALEZ-IZAL M，MALANDA A，GOROSTIAGA E，et.al.Electro⁃myographic models to assess muscle fatigue[J].Journal of Electromyogra⁃phy and Kinesiology，2012，22：501-512.

[7]GONZALEZ-IZAL M，MALANDA A，AMEZQUETA N，et.al.EMG spec⁃tral indices and muscle power fatigue during dynamic contractions[J].Journal of Electromyography and Kinesiology，2010，20：233-240.

[8]LUTTMAN A，JGER M，LAURIG W.Electromyographical indication of muscular fatigue in occupational field studies[J].International Journal of Industrial Ergonomics，2000，25（6）：645-660.

[9]BONATO P，ROY S H，KNAFLITZ M，et.al.Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cy⁃clic dynamic contractions[J].IEEE Trans Biomedical Engineering，2001，48（7）：745-753.

[10]王笃明，王健，葛列众.肌肉疲劳的sEMG时频分析技术及其在工效学中的应用[J].航天医学与医学工程，2003，16（5）：387-390.

[11]牟永阁，彭承琳，郑小林，等，肌肉动态收缩期间表面肌电信号的时频分析[J].生物物理学报，2004，20（4）：323-328.

[12]李世明，许全盛，翟佳丽，等.基于sEMG时频分析的递增负荷诱导肌肉周期动态疲劳估计[J].中国体育科技，2016，52（3）：48-55.

[13]TALEBINEJAD M，CHAN A D，MIRI A.A Lempel-Ziv complexity measure for muscle fatigue estimation[J].Journal of Electromyography and Kinesiology，2011，21：236-241.

[14]CASHABACK J G，CLUFF T，POTVIN J R.Muscle fatigue and contrac⁃tion intensity modulates the complexity of surface electromyography[J].Journal of Electromyography and Kinesiology，2013，23：78-83.

[15]GOLDBERGER A L，PENG C K，LIPSITZ L A.What is physiologic complexity and how does it change with ageing and disease?[J].Neuro⁃biol，2002，23（1）：23-26.

[16]EDUARDO L，SILVA V，CAETANO B，et.al.Multiscale entropy-based methods for heart rate variability complexity analysis[J].Physica A，2015，422：143-152.

[17]TSAIA P H，LIN C，TSAO J，et.al.Empirical mode decomposition based detrended sample entropy in electroencephalography for Alzheimer’s disease[J].Journal of Neuroscience Methods，2012，210：230-237.

[18]MOLINA A，PARRO S I，SORIANO M F，et.al.Multiscale Lempel-Ziv complexity for EEG measures[J].Clinical Neurophysiology，2015，126：541-548.

[19]RICHMAN J S，MOORMAN J R.Physiological time-series analysis us⁃ing approximate entropy and sample entropy[J].American Journal of Physiological Heart Circulation，2000，278（6）：H2039-H2049.

[20]PICO A M，FRAU D C，MARTINEZ P M，et.al.Influence of QRS com⁃plex detection errors on entropy algorithms.Application to heart rate variability discrimination[J].computer methods and programs in bio⁃medicine，2013，110：2-11.

[21]ZHANG X，ZHOU P.Sample entropy analysis of surface EMG for im⁃proved muscle activity onset detection against spurious background spikes[J].Journal of Electromyography and Kinesiology.2012，22：901-907.

[22]COSTA M，GOLDBERGE A L，PENG C K.Multiscale entropy analysis of complex physiologic time series[J].Physical Review Letter，2002，89（6）：1-4.

[23]COSTA M，PENG C K，GOLDBERGE A L.Multiscale analysis of heart rate dynamics：entropy and time irreversibility measures[J].Cardiovas⁃cular.Engineering，2008，8（2）：88-93.