一类含参数紧支撑正交小波的构造

张丽娴，杨守志

（汕头大学数学系，广东汕头515063）

一类含参数紧支撑正交小波的构造

张丽娴，杨守志

（汕头大学数学系，广东汕头515063）

本文提供了一种新的尺度函数构造方法.通过两个已知的正交两尺度符号简单的加权平均得到一个新的尺度符号，所构造的尺度符号能够生成一个尺度函数.这尺度函数具有正交性、紧支撑性，且生成L2上的一个多分辨分析，对应的正交小波生成L2上小波空间.这种构造方法使得在同一区间长度上的小波具有无穷种，丰富了小波的种类.

尺度函数；小波；正交性；多分辨分析；小波空间

0 引言

上世纪80年代初Morlet[1]首次提出小波这个概念，主要用于地质勘探.Meyer[2-3]在Morlet的方法进行深入研究，使得小波分析得到突破性发展.随后，各个领域专家和学者开始研究小波，且与各自领域相互结合，形成了如今小波在各领域广泛使用的状况.由于小波具有较好的应用前景，许多学者仍继续研究，Daubechies[4-5]提出一类紧支撑正交小波基的构造.Chui[6-8]给出了一类紧支撑样条小波的构造.Li[9]等构造了任意长度的正交小波的低通滤波器的系数.为了得到更好的性质，文献[10]提出新平稳双正交样条小波的概念.Zarmehi[11]等构造出有界区间上匹配的多结B样条小波.

本文提供了一种含参数的正交尺度函数构造方法.随着参数选择的不同，在同一区间长度所构造的小波也不一样.这种构造方法使得在同一区间长度上，具有无穷多种小波，大大地丰富了小波的种类，给优化应用提供了更多的选择.

1 新紧支撑正交尺度函数的构造

定义1假设{Vj（j∈Z）}为L2（R）的闭子空间，如果Vj满足：

（1）一直单调性：…⊂V-2⊂V-1⊂V0⊂V1⊂V2⊂…⊂L2（R）；

（2）渐进完全性：∩j∈ZVj=0，；

（3）伸缩规则性：φ（x）∈Vj⇔φ（2-jx）∈V0，j∈Z；

（4）平行不变性：φ（x）∈V0⇔φ（x－k）∈V0，对所有的k∈Z.

那么Vj称为L2（R）上的一个多分辨分析.

对上述的φ（x）∈V0，存在唯一序列pk∈l2（Z），使得

称φ是尺度函数

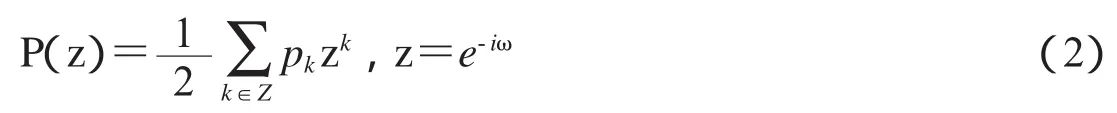
称为尺度函数φ的两尺度符号.

为了构造的需要，下面引入两个结果.

Cohen条件[4-5]设P（ω）形如（2）式的一个多项式，若满足下列条件：

（1）P（0）=1；

则P（ω）是正交尺度函数的符号.

Riesz引理[6]令a0，…，aN∈R，而且aN≠0，使

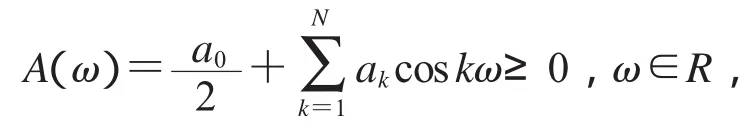
那么存在具有实系数且精确次数为N的一个多项式

1.1 新尺度符号的构造

定理1设P1（ω）和P2（ω）是满足Cohen条件的两个尺度符号.构造，其中∈[0，1]，那么Pne（wω）是一个新的正交尺度符号.

证明：

（1）显然Pnew（ω）满足Cohen条件（2）.

由Cohen条件和Riesz引理可知Pne（wω）是正交尺度符号.

为了方便，设

2 新的尺度函数性质

2.1 对应的尺度函数和小波函数

设φnew是Pnew（ω）生成的正交尺度函数，其两尺度关系为：

对应的正交小波

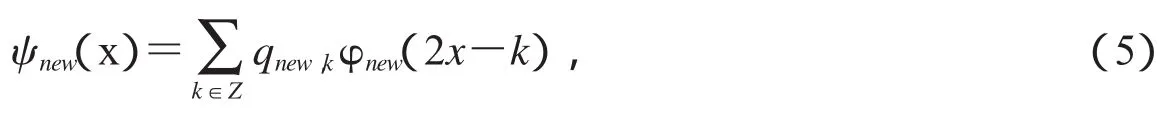
2.2 φnew（x）属于L2（R）

为了证明φnew（x）∈L2（R），只需证明B＜2N－1.（见文献[6]）

设φ1和φ2是两个已知尺度符号P1（ω）、P2（ω）生成的尺度函数，属于L2（R）且逼近阶分别为N1，N2，N1≤N2，那么P1（ω）、P2（ω）有下面的形式：

其中S（10）=1与S（1）≠1，S（20）=1与S（2）≠1.

由于φ1和φ2属于L（2R），所以分别有.

因为

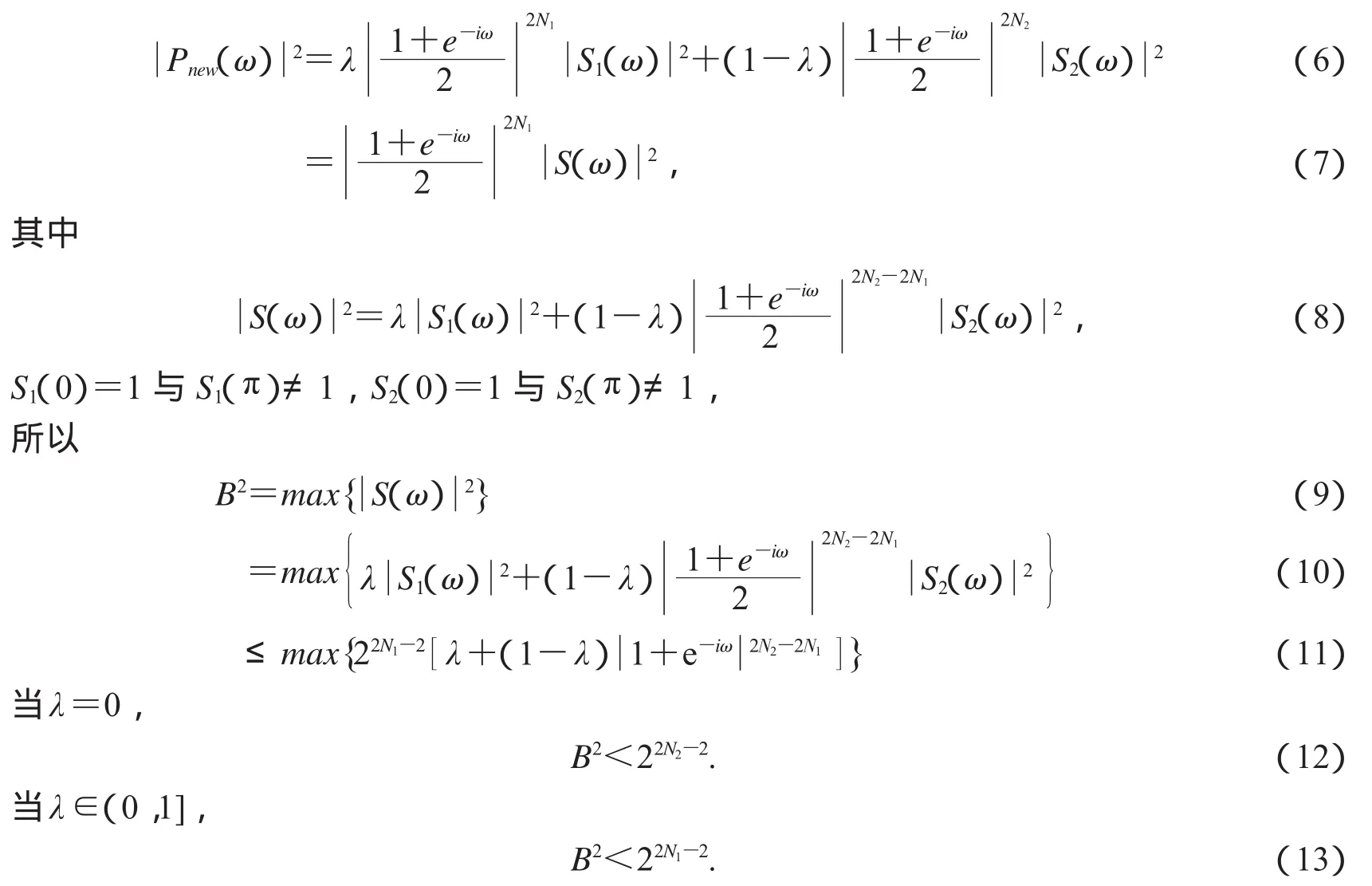
所以φnew（x）∈L2（R）.

2.3 φnew的逼近阶

定理2假设P1（ω）和P2（ω）满足（2）式，由P1（ω）和P2（ω）分别生成的尺度函数φ1和φ2逼近阶分别为N1，N2，且N1＜N2，

证明：因为φ1和φ2逼近阶分别为N1，N2，等价于：

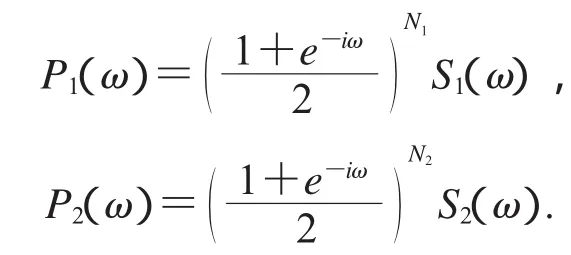
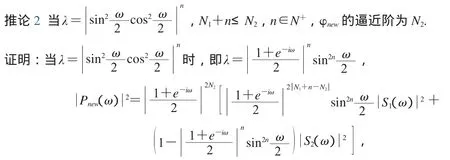
所以，φnew逼近阶为N2.

3 例子

以Haar、Db2的尺度符号P1（ω）和P2（ω）为例子，其中，那么

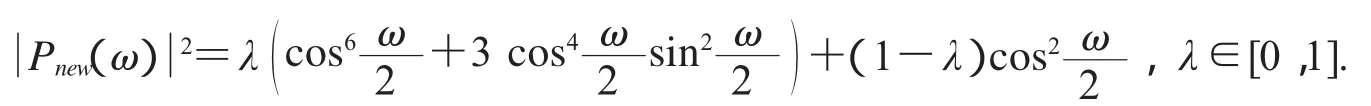
表1分别为参数取0，0.2，0.4，0.6，0.8，1所对应的尺度系数.

表1 一些取值所对应的尺度系数

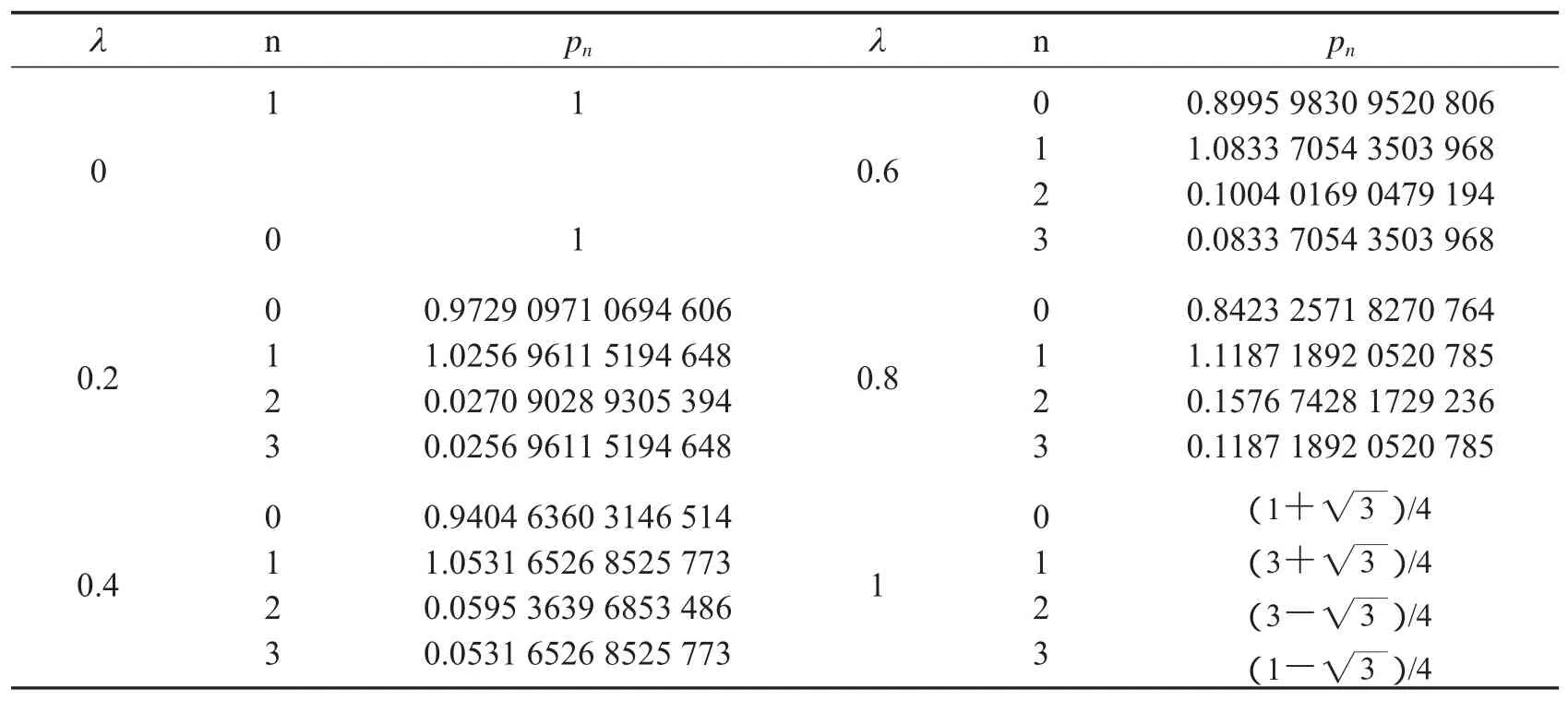
表1 一些取值所对应的尺度系数

n pnn pn0 0.2 1 0 0 1 2 3 1 1 0.9729 0971 0694 606 1.0256 9611 5194 648 0.0270 9028 9305 394 0.0256 9611 5194 648 0.6 0.8 0 1 2 3 0 1 2 3 0.8995 9830 9520 806 1.0833 7054 3503 968 0.1004 0169 0479 194 0.0833 7054 3503 968 0.8423 2571 8270 764 1.1187 1892 0520 785 0.1576 7428 1729 236 0.1187 1892 0520 785 0 1 2 3 0.9404 6360 3146 514 1.0531 6526 8525 773 0.0595 3639 6853 486 0.0531 6526 8525 773 0.4 1 0 1 2 3■）/4（3＋3（1＋3■）/4（3－3■）/4（1－3■）/4

图1-3是参数分别取值为0，0.6，1的尺度和小波图像.左为尺度涵数图像，右为小波涵数图像.

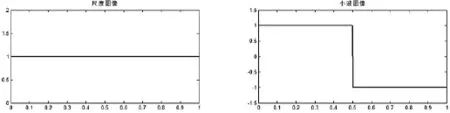
图1 =0，左为尺度函数，右为小波函数

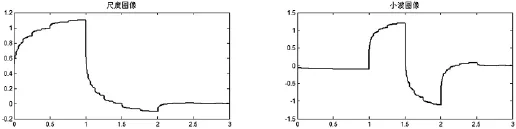
图2 =0.6，左为尺度函数，右为小波函数

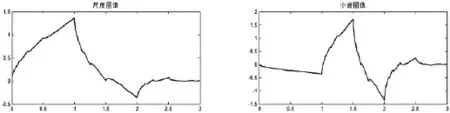
图3 =1，左为尺度函数，右为小波函数

由Riesz引理知系数：

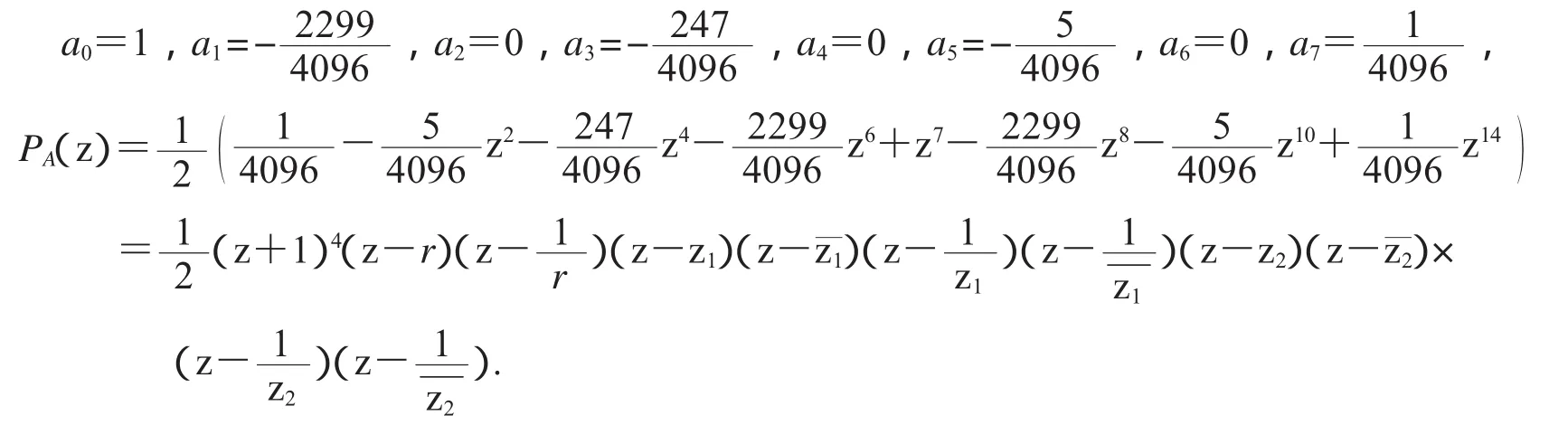
其中r=-0.2565，z1=0.0087＋0.2409i，z2=0.2558－0.0662i，选择单位圆内的点

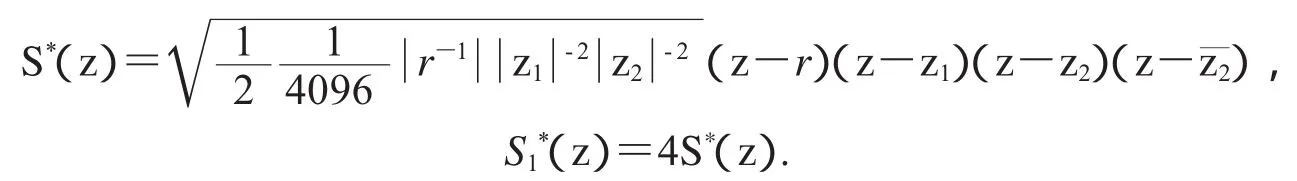
生成的尺度符号为：

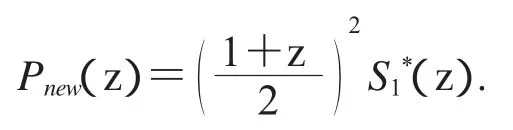
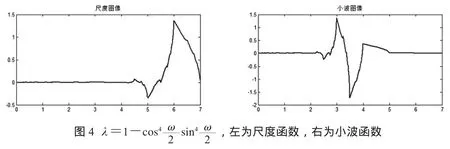
图4为对应的尺度函数和小波图像.

[1]GROSSMANNA，MORLET J.Decomposition of hardy functions into square integrable wavelets of constant shape[J].SIAM J Math Anal，1984，15（4）：723-736.

[2]MEYERY.Waveletsandfast numerical algorithms[J].Handbookof Numerical Analysis，1997，5：639-713.

[3]MEYER Y.Orthonormal wavelets[M].Berlin：Springer，1989.

[4]DAUBECHIES I.Orthonormal bases of compactly supported wavelets[J].Comm Pure Apple Math，1988，41（7）：909-996.

[5]DAUBECHIES I.Ten lectures on wavelets[M].Philadelphia：SIAM，1992.

[6]CHUI C K.An introduction to wavelets[M].Boston：Academic Press，1992.

[7]CHUI C K，HAN B，ZHUANG X.A dual-chain approach for bottom-up construction of wavelet filters with any integer dilation[J].Applied And Computational Harmonic Analysis，2012，33（2）：204-225.

[8]CHUI C K，LIAN J A.Construction of orthonormal multi-wavelet with additional vanishing moments[J].Advance In Computational Mathematics，2006，24（1/4）：239-262.

[9]LIJ P，TANG Y Y.Generalanalytic construction for wavelet low-passed filters[J].International Computer Conference On Wavelet Active Media Technology And Information Processing，2001，2251：314-320.

[10]PRIMBSM.New stable biorthogonalspline-waveletson the interval[J].ResultsIn Mathematics，2010，57（1/2）：121-162.

[11]ZARMEHIF，TAVAKOLIA.Construction ofthe matched multiple knotB-spline wavelets on a bounded interal[J].International Journal of Computer Mathematics，2015，92（8）：1688-1714.

Construction of a Class of Compactly Supported Orthogonal Wavelet with Parameter

ZHANG Lixian,YANG Shouzhi
（Department of Mathematics，Shantou University，Shantou 515063，Guangdong，China）

A newmethod for constructing scaling function is presented.A newscale symbol by two known scale symbols is obtained.The new scale symbol can generate a scale function.The scaling function has orthogonalityand compact support.A L2multiresolution analysis and wavelet orthogonal wavelet spaceis generated.Thewaveletin thesameinterval oflength with infiniteis obtained.

scale function;wavelet;orthogonality;multi-resolution analysis;wavelet space

O29

A

1001-4217（2017）01-0015-07

2016-03-16

张丽娴（1992—），女，广东东莞人，在读硕士研究生.研究方向：小波分析及应用.E-mail：14lxzhang@stu.edu.cn.

广东省自然基金资助项目（2015A030313443）