均质杆绕固定点转动问题探析

陈志军

(安徽省绩溪中学 安徽 宣城 245300)

均质杆绕固定点转动问题探析

陈志军

(安徽省绩溪中学 安徽 宣城 245300)

均质杆绕固定点转动问题，不是简单的质点圆周运动问题，需要考虑杆的质量以及分布情况，对学生的分析、解决问题的能力要求比较高．灵活运用微元法、积分思想方法和平均值法解决均质杆绕固定点转动问题，可以有效提高学生的思维能力和解决问题的能力，帮助学生形成物理学科核心素养．

均质杆 转动 微元 积分

对于均质杆绕固定点转动问题，由于要考虑杆的质量及其分布情况，再加上中学生在数学知识上的局限性，这类问题的解决对学生的能力提出了较高的要求，许多学生对此感到非常困惑、无从下手．微元法和积分思想方法是从部分到整体的科学思维方法，通过微元分析整体，将其分解为众多微小的遵循相同规律的元过程，再对这些元过程进行必要的数学物理思想和方法处理．使用微元法和积分思想方法是分析和解决均质杆绕固定点转动问题的基本方法，能达到巩固知识、加深认识、有效提高学生的思维能力和解决问题能力的目标．本文分别从微元法、积分思想方法和平均值法的角度分析均质杆绕固定点转动问题．

【例1】 如图1所示，在水平地面上放一根长为l，质量为m的均质木棒，棒与地面间的动摩擦因数为μ，现用力使木棒绕其一端缓慢地在水平地面上转过θ角，求该过程需要做多少功？

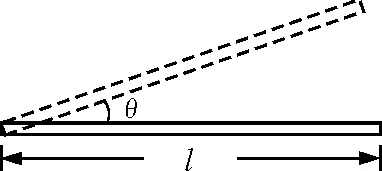
图1 例1题图

分析：均质木棒绕绕其一端(固定点)转动，不是质点的圆周运动，棒上各部分位移不同，各部分所受摩擦力做的功也不同，可以采用分割木棒的微元法进行分析求解．

解法一：利用微元法[1]

将均质木棒分成n段，n→∞，每一段的质量

由于木棒缓慢转动，可以认为木棒动能不变且趋向于零，转动过程中，根据动能定理，外力所做的功等于整个木棒克服摩擦力所做的功，即等于n段木棒克服摩擦力所做功之和．因此外力所做功

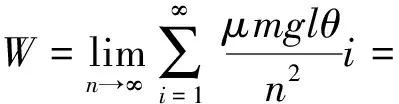
解法二：利用积分思想方法

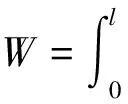
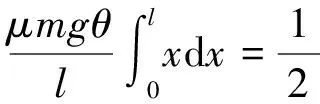
解法三：利用平均值法

通过前面微元分析可知，木棒绕一端固定点转动，木棒上各点的位移(即转过的弧长)与该点到木棒转轴的距离成线性变化，木棒上各点转动的位移的平均值可以等效为木棒中点转过的位移，所以整个木棒克服摩擦力所做功的总功，即外力所做功

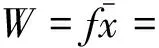
【例2】 如图2所示，一根长为l、质量为m的均质木棒，在水平面内以角速度ω绕通过木棒一端的竖直轴匀速转动，木棒所具有的转动动能为多大？

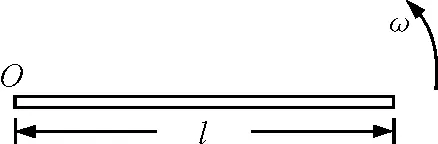
图2 例2题图

分析：该问题与题1类似，木棒绕竖直轴O转动时，棒上各部分转动速度不一样，各部分动能也不一样，同样需要采用分割木棒的微元法分析求解．

解法一：利用微元法[1]

整个木棒的动能为各小段木棒的动能之和，即

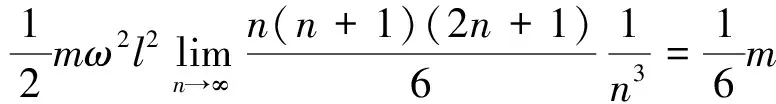
解法二：利用积分思想方法

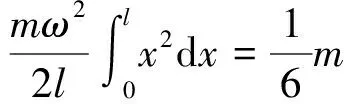
通过前面微元分析可知，在木棒绕固定点O转动时，木棒上各点的线速度随离开转轴O点的距离成线性变化，整个木棒的平均线速度可以等效为木棒中点的线速度，那么本题是不是也能用平均值法解答呢？学生很容易认为动能

毫无疑问，这是一个错误的结论，原因是虽然木棒上各点的线速度随离开转轴的距离成线性变化，但速度的平方并不是随离开转轴的距离成线性变化，因此不能利用平均值法求解动能．

【例3】 如图3所示，匀强磁场的磁感应强度为B，一长度为l的导体棒绕固定端点O以角速度ω在垂直磁场的平面内匀速转动，求该导体棒因转动产生的感应电动势．

图3 例3题图

分析：该导体棒虽然不一定是均质导体棒，但棒上每一点切割磁感线的线速度与题2很类似，该棒切割磁感线产生感应电动势的求解仍可采用微元法和积分思想进行求解．

解法一：利用微元法

导体棒转动过程中产生的总的感应电动势等于n段导体切割产生的感应电动势之和，即

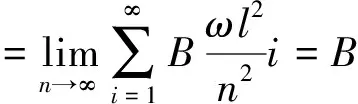
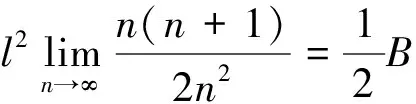
解法二：利用积分思想方法

在导体棒上距离转轴x处，取微元长度为dx，微元dx切割磁感线的速度为ωx，则整个导体棒切割磁感线产生的感应电动势

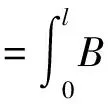
解法三：利用平均值法

导体棒绕端点O匀速转动时，棒上各点的速度随离开木棒端点O的距离成线性变化，所以整个导体棒切割磁感线的平均线速度可等效为导体棒中点的线速度，因此，整个导体棒切割磁感线产生的感应电动势

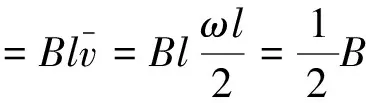
【例4】 如图4所示，质量为M、长度为d的均匀细棒AC放在旋转圆盘ED上，盘以恒定角速度ω旋转．棒AC的轴和盘的半径方向重合，棒的A端连着一根拴有重物的绳子，质量为m的重物正好悬在盘的旋转轴O上，棒与盘的动摩擦因数为μ，计算棒的A端距转轴O的最大和最小距离，此棒不再沿盘的半径方向移动[2]．

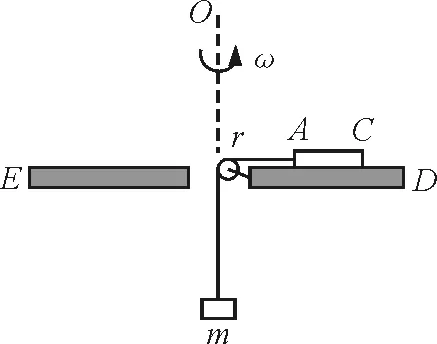
图4 例4题图

分析：随圆盘一起做匀速圆周运动的是均匀细棒，细棒的线速度从A到C逐渐增加，细棒上每质元做圆周运动的半径都不同，需要采用分割细棒的微元法分析求解．

解法一：利用微元法

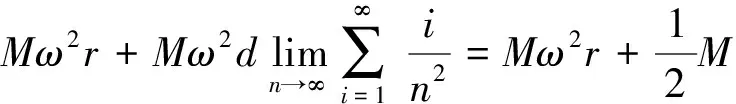
解得

如果上式结果r<0，则r的最小值取零，即细棒左端与中心O点重合，故

当M有向外做离心运动的趋势时，细棒所受的静摩擦力方向沿半径方向向内，为保证细棒不滑动，临界情况是静摩擦力达到最大时，细棒的旋转半径达到最大，即此时r取最大值，最大静摩擦力近似等于滑动摩擦力μMg，根据牛顿运动定律得到

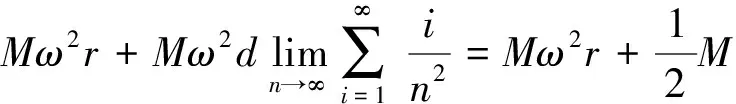
解得

故r的最大值

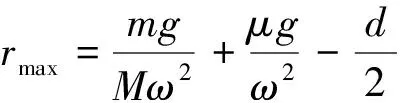
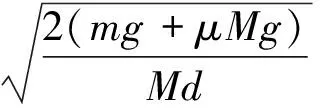
解法二：利用积分思想方法

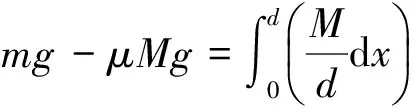
解得

如果上式结果r<0，则r的最小值取零，即细棒左端与中心O点重合，故

当M有向外做离心运动的趋势时，细棒所受的静摩擦力方向沿半径方向向内，静摩擦力达到最大时，细棒的旋转半径最大，即此时r取最大值，根据牛顿运动定律得到

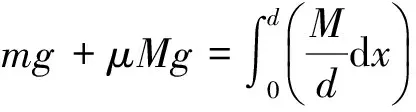
解得

故r的最大值

其中

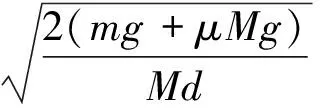
解法三：利用平均值法

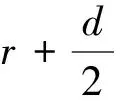
由此可解得

如果r<0，则r的最小值取零.

当M有向外做离心运动的趋势时，根据牛顿运动定律得到

由此可解得

其中

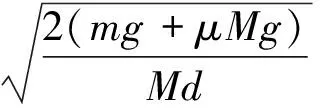
均质杆绕固定点转动问题，必须考虑杆的质量及其分布情况，利用微元法、积分思想方法和平均值法，可以有效分析和解决此类问题，加深学生对科学思维方法的认识和运用，丰富处理物理问题的手段，锻炼学生的思维、推理和运算等能力，形成物理学科核心素养．

1 王溢然,许洪生.分割与积累(中学生物理思维方法丛书8).合肥:中国科学技术大学出版社,2015.8

2 程稼夫.中学奥林匹克竞赛物理教程·力学篇(第2版).合肥:中国科学技术大学出版社,2015.11

2016-08-23)