集成式电子液压制动系统液压力变结构控制*

余卓平,韩 伟,熊 璐

(1.同济大学汽车学院,上海 201804; 2.同济大学新能源汽车工程中心,上海 201804)

集成式电子液压制动系统液压力变结构控制*

余卓平,韩 伟,熊 璐

(1.同济大学汽车学院,上海 201804; 2.同济大学新能源汽车工程中心,上海 201804)

针对集成式电液制动系统液压力控制中系统受到摩擦等非线性因素的影响而控制精度低的问题,简化了系统模型,并基于Stribeck摩擦模型重点对造成系统非线性特性的摩擦力进行分析。然后设计了针对I-EHB系统的抗积分饱和变结构控制方法,通过AMESim和Simulink联合仿真验证控制算法的有效性。最后搭建了IEHB系统样机和试验平台,进行了硬件在环台架试验,验证了控制算法的正确性。结果表明,采用抗积分饱和变结构控制器后,系统跟踪变幅值或变频率的目标信号的效果良好,控制精度高,系统性能得到明显改善。

集成式电液制动系统;液压力控制;Stribeck摩擦模型;抗积分饱和变结构控制

前言

随着汽车电子技术的不断发展和汽车系统的集成化,在航空和军事运用中逐渐成熟的线控制动技术开始逐渐被应用到汽车上。汽车线控系统的应用可极大地提高汽车驾驶的安全性、可靠性和稳定性。

作为线控技术与液压制动系统相结合的产物,从结构上看,电-液制动系统(electro-hydraulic brake system,EHB)主要由电控系统和液压执行系统两大基本模块组成。其中,电控系统主要由电子控制单元(ECU)和一系列传感器组成,其核心功能是判断驾驶员的制动意图,并通过相应的控制程序向液压执行系统中各执行器发出控制指令,同时电控系统也通过CAN总线与其他车载电控系统进行通信和数据交换;液压执行系统主要由液压泵、蓄能器、电磁阀、制动主缸和制动轮缸等组成,各执行器接收来自ECU的控制指令,分别进行相应的操作以实现对轮缸压力的精确控制[1]。

对于EHB系统,国内部分高校、科研单位做了初步的研究,且多为解决方案的提出和仿真研究,缺乏对EHB系统进行深入的试验研究和系统整体开发的能力。文献[2]中设计了一套电液制动系统,该系统通过踏板位移传感器获取驾驶员制动意图,并采用PID算法对液压系统压力进行主动控制,仿真和试验结果均证明,该系统具有良好的瞬态响应和稳态响应能力,并可利用滑移率控制实现ABS防抱死的功能。

文献[3]中提出了一种分布式电液制动系统的概念,并利用AMESim,Simulink和CarSim软件搭建系统的仿真模型。在搭建的系统实验台架上,运用PID控制方法进行了液压压力控制实验,实验结果显示该系统具有建压能力强、响应速度快,压力跟踪准确的优点。

集成式电-液制动系统(integrated-electro-hydraulic brake system,I-EHB)不同于目前应用较多的泵式电液制动(P-EHB)系统,它摒弃了高压蓄能器及其高速开关控制阀系,节省了成本并避免了泄漏风险[4],从成本和可靠性上更具优势。

由于I-EHB系统刚刚兴起,所以国内外研究主要集中于ESC和P-EHB。相关研究如文献[5]中对P-EHB进行了相关建模及动态特性研究,文献[6]中对P-EHB系统的跟随特性进行了实验研究。

然而由于I-EHB系统采用了电机和减速机构,存在非线性时变因素,使其精确的动态液压力控制比较困难。且I-EHB由于其结构特征使其不能采用P-EHB或者电子稳定系统(electronic stability control system,ESC)的液压力控制方法。此外,I-EHB系统的工作受温度、湿度和载荷扰动等多重不确定因素的影响,容易产生振荡。因此要求液压力控制系统对外界不确定的扰动有较强的适应性,同时满足法规要求。因此,对于I-EHB的液压力控制的研究有较高的实际应用需求和价值。国内对于I-EHB的研究,如文献[7]中利用基于系统改进的田口方法,提出一种集成式电液制动系统鲁棒性液压力控制方法,系统响应迅速,在500次试验内均保持稳健。

本文中简化了I-EHB系统模型,并基于Stribeck摩擦模型重点对造成系统非线性特性的摩擦力进行分析。然后设计了针对I-EHB系统的抗积分饱和变结构控制方法[8],先通过AMESim和Simulink联合仿真验证控制算法的有效性。最后搭建了I-EHB系统样机和试验平台,进行了硬件在环台架试验,验证了控制算法的正确性。

1 方案设计

本文中所采用的I-EHB系统的方案简图如图1所示。

图1 I-EHB系统方案简图

该系统主要包括制动踏板、踏板位移传感器、踏板模拟器、电机、减速传动机构、制动主缸和液压力传感器等。解耦腔起系统解耦的作用,即实现正常制动时制动踏板与制动主缸不固连。

正常工作时,驾驶员踩下制动踏板,踏板感觉模拟器模拟踏板感觉,同时解耦腔内预留的空行程使得制动踏板不再直接与制动主缸相连。同时电控单元(electric control unit,ECU)根据踏板位移信号和制动能量回收系统中的再生制动力信号计算液压制动力和I-EHB系统电机转矩作为指令发给电机。电机通过减速机构推动主缸建立压力,制动液流向各轮缸而产生制动力。

2 系统简化与分析

2.1 系统模型简化

由于系统各部分的数学模型过于复杂,不利于对系统的有效控制。为满足对该系统的控制要求,本文中先对系统模型进行简化。由于制动管路对系统压力的影响非常小,可以忽略制动管路模型。

将系统物理模型进行简化,如图2所示。机械部分表示滚珠丝杠副减速机构,液压部分表示制动主缸和制动轮缸。电机输出转矩作用于机械部分,机械部分主缸推杆输出力作用于液压部分。简化的系统数学模型为

图2 系统数学模型简化示意图

式中:m为机械部分的等效质量;c为机械部分的等效阻尼; k为机械部分的等效刚度;x,和分别为液压部分制动腔活塞的轴向位移、轴向速度和轴向加速度;Tm为电机输出转矩;i为机械部分的传动比;r为机械部分等效半径;p为液压部分的液压力;A为液压部分活塞的等效面积;f(p,x,)表示机械部分和液压部分的摩擦力总和,是该系统非线性因素的来源。

一维可压缩流体的数学模型为

制动腔连续流量方程为

式中:V为制动腔内液体体积;Ke为体积弹性模量;p·为制动腔内液体的压力变化率;ΔQ为液体体积流量的变化量;Q为液体体积流量;γ为制动腔的泄漏系数。

联立式(1)～式(3)得到简化后的数学模型为

2.2 系统非线性特性分析

由式(4)可知,摩擦力对系统的影响很大。为找出适合该系统的控制方法,首先基于Stribeck摩擦模型对系统非线性特性进行分析[9]。

I-EHB系统的减速机构采用滚珠丝杠副。它的一个较大的弱点是存在摩擦,这也正是I-EHB液压力控制的难点所在。摩擦力大小取决于多方面的因素,包括接触面的形状、接触物体的材料特性、接触物体之间相对滑动速度和接触物体之间的润滑状态等。将物体接触面之间看成是“突点”,物体之间的接触力与物体之间的滑动速度的函数即是摩擦力的模型,按照物体之间接触速度的不同和润滑状态的不同将摩擦力分成4个阶段,不同阶段摩擦力具有不同特性,结合图3和式(5)说明不同阶段摩擦力的变化。

(1)接触面弹性变形阶段:物体相对滑动之前,受到摩擦力的约束处于相互接触的状态,物体相对滑动的位移是一个微位移的状态,摩擦力是微位移的线性函数,静摩擦力在接触断开之后达到一个峰值,这个值就是最大静摩擦力。

(2)边界润滑阶段:当外力达到一定阶段,原来相互接触的物体被分离,两个物体之间发生相对滑动,这个时候速度还是很低的,相互接触的“突点”不断地断开和重新形成,此时的摩擦力大小与物体之间的接触状态有关。

(3)部分润滑阶段:当物体之间的相对滑动速度逐渐增大,物体之间润滑的边界层增厚,此时相互接触的“突点”不断减少,这个过程中既有液体润滑又有“突点”接触,此时的摩擦力大小与物体之间的相对滑动速度成反比,即负斜率特性,此时的摩擦力小于全润滑阶段的摩擦力。

(4)全液体润滑阶段:随着速度的增加,接触面完全被液体润滑层分开,此时的摩擦力主要由黏性摩擦力决定,主要取决于速度和润滑剂的状态。

图3 系统摩擦力特性曲线

式中:Ff为摩擦力;为第2和第3阶段过渡点的临界速度;为第3和第4阶段过渡点的临界速度; k0为比例系数;k1为接触状态因子;fmax为最大静摩擦力;fc为库伦摩擦力;cf为阻尼系数。

从式(5)可以得出,摩擦力的非线性很强,会随着位移和速度等参数的变化而变化。尤其对于IEHB这类运行速度和方向变化较大的系统,其摩擦力会时常在静摩擦力与动摩擦力之间切换,容易引起极限环现象,使系统不稳定。同时,系统的接触状态和阻尼系数会随着温度、气候和外界干扰而变化,这同样增加了系统的控制难度。

3 液压力变结构控制

引入抗积分饱和变结构控制方法对液压力进行控制。控制系统结构框图如图4所示。

图4 控制系统结构框图

3.1 控制算法的原理

考虑标量非线性系统:

式中:x为系统状态;f连续,且满足局部Lipschitz条件[10],Lipschitz常数为Lf;u为系统的控制输入;y为系统的受控输出。

设计控制律使系统输出y跟踪yr=xr,定义跟踪误差为e=x-xr。控制器的目标是使跟踪误差收敛至零。系统误差为

引入新变量s和ρ:

式中:k0和θ为正常数,并且满足

其中饱和函数定义为

设计镇定控制律为

式中:fm(xr)表示实际模型f(x)的名义项,用来抵消f(x);cap＞0,并且满足:

3.2 控制算法的稳定性分析

本文中所设计的式(10)控制律为一带抗饱和策略的变结构控制:控制器在未发生饱和时施行比例积分控制。然而,由于系统参数变化、外界干扰和建模不精确等因素都会对系统镇定的稳定性产生影响,长时间无法镇定可能会使积分项不断增大,从而导致执行器过早饱和,损害系统的瞬态响应甚至是稳定性;抗饱和策略能保证在执行器饱和以后仍可使系统镇定收敛。下面进行控制算法的稳定性分析。

系统稳定性将从控制器饱和与未饱和两方面进行分析。

(1)当|s|≥θ时,所设计的控制器参数只要满足一定条件,就能保证|s|在有限时间内收敛到(0, θ)范围内,且此后都在该范围内。

记Ms为误差与误差积分流形,即

其几何意义如图5所示。

图5 误差与误差积分流形图

记Mρ为误差积分的集合,即

则,只要 ρ(t0)≤θ/k0,由式(13)知,对任意 t＞t0,恒有:

因此,集合Mρ为不变集,系统状态的变动被限定在AC和BD两平行线之间:即s的变动范围为s≥θ(线段AB以上部分)和s≤-θ(线段CD以下部分),设α=[k01]为与线段AB相垂直且指向流形Ms以外的向量。

在线段AB以上,s向流形Ms运动,只要满足式(15)即可:

对式(15)展开,有

因此,结合式(15),cap须满足条件:

在线段CD以下,s向流形Ms运动,同理,只要cap满足条件:

综合条件式(17)和式(18)可得

(2)当|s|＜θ时,所设计的控制律为比例积分控制,能够保证系统的状态e被镇定到原点,系统渐近收敛。

将式(10)控制律代入式(7)误差系统,则误差系统可被转化为

显然,上述系统方程为典型的 Van der Pol方程,可视为一个质量 弹簧 阻尼系统。因此,只要

则系统一定是渐近稳定的。

由于系统函数f连续,且满足Lipschitz常数为Lf的局部Lipschitz条件,所以,式(21)变为

3.3 液压力跟踪控制算法的设计

第3.2节给出了一般标量非线性系统跟踪控制算法的原理和理论分析,通过以上分析可以看出,本文中所设计的控制律从理论上能够保证系统的跟踪渐近稳定。下面将该控制律应用在I-EHB系统的液压力跟踪控制上,即对I-EHB系统的液压力进行跟踪控制。

根据I-EHB系统动力学关系及流量方程,被控系统的状态方程为

如果

现需要设计一个可靠实用的控制律,使实际液压力能跟踪目标液压力 pref,以保证系统的闭环稳定。

根据前文的理论分析,引入新变量:

设计一个稳定的控制律:

式中:cap,k0和θ均为正数。

定义等效力矩为

切换力矩为

由于公式中摩擦力f(p,x,x·)的名义模型不易求出,所以采用颤振信号补偿系统的摩擦力。摩擦补偿最常用的控制方法是基于摩擦模型的摩擦力补偿控制,如文献[9]中利用摩擦颤振补偿提高了系统的定位精度;文献[11]中利用摩擦补偿方法对IEHB系统进行液压力优化控制研究,并对不同工况下的颤振信号幅值和频率进行优化,使摩擦爬行现象消失,系统的线性度增强,系统性能提高。

进一步的研究和实验发现,颤振信号的幅值对系统稳定性和摩擦非线性的消除有很大影响。幅值过大会导致系统不稳定,而幅值过小则摩擦非线性严重。幅值的大小与液压力有关,故采用自适应颤振信号进行摩擦补偿,本文中颤振信号幅值与压力成线性关系:

式中:Amp为颤振信号幅值;a和b为待定系数。

由于实际中x和 x··很小以至于传感器测量噪声大,所以对它们进行估计。引入等效力矩增益

由前面的理论分析得cap,k0和θ满足以下条件:

式中:xmax为估计的液压部分制动腔活塞的最大轴向位移;LF为系统函数的Lipschitz常数,为非负数。

此外,需要注意的是,cap的取值还受到电机当前转速下最大转矩的限制,即外特性的限制,图6给出了本文中所使用的电机的外特性曲线。

图6 电机的外特性曲线

4 仿真研究

基于以上理论分析,抗积分饱和变结构控制算法能跟踪目标液压力信号,且系统趋于稳定表明该控制算法能够有效地对I-EHB系统进行液压力控制。对此,先通过计算机仿真的方法验证该控制算法的可行性。具体做法是在AMESim中建立I-EHB系统的物理模型,在Matlab/Simulink中建立该控制算法的数学模型,最后用AMESim和Simulink联合仿真验证该控制算法的有效性和正确性。I-EHB系统在AMESim中的物理模型如图7所示。

图7 系统仿真模型

仿真研究的思路是从目标液压力幅值和频率的角度验证该控制算法的有效性,所以设计了幅值分别为1,2和3MPa的目标阶跃信号和频率分别为0.5,1.0和2.0rad/s的目标正弦信号跟踪仿真。其中,在0.5s时向电控单元ECU输入目标阶跃信号。跟踪仿真如表1所示。

表1 系统液压力控制仿真目标信号

图8 幅值1MPa的阶跃信号跟踪仿真结果

图8～图10为阶跃信号跟踪的仿真结果。可以看出,系统能很好跟踪目标阶跃信号,系统最终收敛于目标压力。对于变幅值的目标信号跟踪,该控制方法是可行的。

图11～图13为正弦信号跟踪的仿真结果。可以看出,系统液压力响应总体趋势基本一致,虽然存在抖动,但系统仍保持稳定。因此对于变频率的目标信号跟踪,该控制方法是可行的。

图9 幅值2MPa的阶跃信号跟踪仿真结果

图10 幅值3MPa的阶跃信号跟踪仿真结果

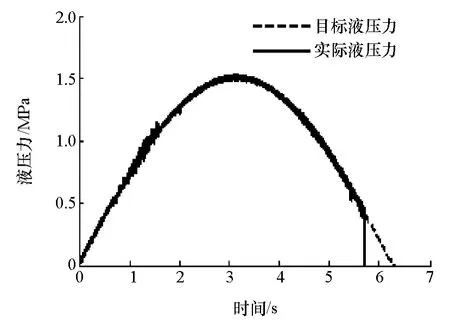
图11 频率0.5rad/s的正弦信号跟踪仿真结果

5 试验验证

第4节中已通过计算机仿真验证了该控制算法的可行性,下面将通过台架试验及系统性能的具体指标来验证该控制方法是否满足液压力控制的要求。

图12 频率1.0rad/s的正弦信号跟踪仿真结果

图13 频率2.0rad/s的正弦信号跟踪仿真结果

5.1 硬件在环试验平台

为测试系统性能,组建如图14所示的I-EHB系统样机,并在此基础上建立如图15所示的I-EHB系统测试平台。图16为I-EHB系统台架拓扑图。试验台采用踏板位移传感器获取驾驶员的制动意图,之后通过控制器将制动意图换算得到电机转矩进行制动。平台还可通过CAN总线直接控制电机转矩。测试平台采用某款车原配的基础制动系统。

图14 I-EHB系统样机

5.2 试验结果与分析

以该控制算法进行台架试验,对给定的目标液压力信号进行跟踪,观察系统实际液压力响应。台架试验与仿真试验设计相似,分为阶跃信号和正弦信号跟踪。

5.2.1 阶跃信号跟踪

试验工况为在0.5s产生目标液压力阶跃信号,幅值分别为1,5和8MPa,试验结果如图17～图19和表2所示。

图15 I-EHB系统测试平台

图16 I-EHB系统台架拓扑图

图17 幅值1MPa的阶跃信号跟踪试验结果

由试验结果可以看出,实际液压力响应能很好跟踪目标阶跃信号。当目标阶跃信号幅值变化时,系统响应液压力趋于稳定,且闭环系统时域、频域的各项指标都满足要求。

图18 幅值5MPa的阶跃信号跟踪试验结果

图19 幅值8MPa的阶跃信号跟踪试验结果

表2 阶跃信号跟踪试验结果对比

5.2.2 正弦信号跟踪

试验工况为偏置4MPa、幅值4MPa的目标液压力正弦信号,频率分别为0.5,1和2Hz。试验结果如图20～图22和表3所示。

表3 正弦信号跟踪试验结果对比

由试验结果可以看出,当目标正弦信号频率变化时,实际液压力响应能很好跟踪目标正弦信号。当目标正弦信号频率增大时,实际液压力响应的均方根误差增大。由上文系统非线性特性分析可知,该系统由于摩擦带来的非线性很强,当目标信号频率增大时,该系统响应变慢,误差累积增多,故均方根误差增大。但此时的控制效果可以满足要求。

图20 频率0.5Hz的正弦信号跟踪试验结果

图21 频率1.0Hz的正弦信号跟踪试验结果

图22 频率2.0Hz的正弦信号跟踪试验结果

6 结论

由于集成式电子液压制动系统是一个包含许多不确定因素和非线性对象的系统,所以对于该系统的精确动态液压力控制存在困难。本文中简化了系统模型,并基于Stribeck摩擦模型重点对造成系统非线性特性的摩擦力进行分析。然后设计了针对IEHB系统的抗积分饱和变结构控制方法,先通过AMESim和Simulink联合仿真验证控制算法的有效性。最后搭建了I-EHB系统样机和试验平台,进行了硬件在环台架试验,验证了控制算法的正确性。得出结论如下:

(1)仿真研究和台架试验表明利用抗积分饱和变结构控制的液压力控制方法对I-EHB系统的控制效果良好;

(2)利用该控制方法后系统液压力响应可较好地跟踪变幅值和变频率的目标信号,控制精度高,系统性能得到明显改善。

[1] XIONG L,YUAN B,GUANG X,et al.Analysis and design of dual-motor electro-hydraulic brake system[C].SAE Paper 2014-01-2532.

[2] 卓桂荣,林宗浩,张斌.线控电液制动系统技术研究[J].应用科技,2010(2):195-196.

[3] WANG Z,YU L,WANG Y,et al.Prototype of distributed electro-hydraulic braking system and its fail-safe control strategy[C]. SAE Paper 2013-01-2066.

[4] REUTER D F,LLOYD E W,ZEHNDER J W,et al.Hydraulic design considerations for EHB systems[C].SAE Paper 2003-01-0324.

[5] D'ALFIO N,MORGANDO A,SORNIOTTI A.Electro-hydraulic brake systems:design and test through hardware-in-the-loop simulation[J].Vehicle System Dynamics,2006,44S:378-392.

[6] 赵海涛.汽车电子液压制动系统跟随特性的实验研究[D].长春:吉林大学,2011.

[7] 余卓平,徐松云,熊璐,等.集成式电子液压制动系统鲁棒性液压力控制[J].机械工程学报,2015,51(16):22-28.

[8] 周黎.分布式驱动电动汽车驱动防滑控制[D].上海:同济大学,2013.

[9] 孔祥臻,王勇,蒋守勇.基于Stribeck模型的摩擦颤振补偿[J].机械工程学报,2010,46(5):68-73.

[10] KHALIL H K.Nonlinear systems(3rdedition)[M].Prentice Hall,2001:76-97.

[11] 余卓平,徐松云,熊璐,等.基于颤振补偿的集成式电子液压制动系统控制[J].同济大学学报(自然科学版),2015,43(7): 1063-1068.

Variable Structure Control for Hydraulic Pressure in Integrated-electro-hydraulic Brake System

Yu Zhuoping,Han Wei&Xiong Lu
1.School of Automotive Studies,Tongji University,Shanghai 201804; 2.Clean Energy Automotive Engineering Center,Tongji University,Shanghai 201804

In view of the low control accuracy of hydraulic pressure control in integrated electro-hydraulic brake(I-EHB)system due to the effects of nonlinear factor like friction,the system model is simplified and the friction force leading to the nonlinear characteristics of system is emphatically analyzed based on Stribeck friction model.Then an anti-windup variable structure control technique for I-EHB system is designed,and the control algorithm is verified by AMESim/Simulink co-simulation.Finally the prototype and test platform of I-EHB system are constructed and a hardware-in-the-loop bench test is conducted to verify the rightness of control algorithm.The results show that with anti-windup variable structure controller adopted,the system has good effects in tracking target signals of variable amplitude or variable frequency,with high control accuracy and significantly improved performance.

I-EHB;hydraulic pressure control;Stribeck friction model;anti-windup variable structure control

10.19562/j.chinasae.qcgc.2017.01.009

*国家自然科学基金(51475333)资助。

原稿收到日期为2015年11月25日,修改稿收到日期为2016年2月3日。

熊璐,教授,E-mail:xiong_lu@tongji.edu.cn。