一种改进的GMSK信号差分检测算法

朱晓峰，王 伟

（中国空间技术研究院西安分院 陕西 西安710100）

一种改进的GMSK信号差分检测算法

朱晓峰，王 伟

（中国空间技术研究院西安分院 陕西 西安710100）

在Laurent分解的基础上，提出了一种改进的差分检测算法，算法在传统差分检测算法基础上增加Laurent匹配滤波及白化滤波，消除了其它分解子波形对算法性能的影响。仿真结果表明，误码率为 时，文中提出的算法与传统差分检测算法相比有近0.5 dB的信噪比增益，算法复杂度没有明显增加。

GMSK调制；Laurent分解；差分检测；白化滤波

GMSK（高斯最小频移键控）调制信号是一种有记忆的相位连续的恒包络调制信号，它是在MSK（最小频移键控）调制信号的基础上加一级高斯预平滑滤波器实现的，因而其具有带宽窄，带外功率衰减快，频谱利用率高等优点。数字通信系统中，信道带宽有限，因而需要采用频谱利用率高的调制方式，GMSK由于其良好的特性在数字通信系统中得到了广泛的应用。目前，GMSK已经应用到GSM（全球移动通信系统）系统中。

GMSK信号的非相干检测主要有差分检测和最大似然检测两种方式。差分检测算法比较简单，目前在一些性能要求不高的应用中得到了广泛的应用。文献[1-4]介绍了不带反馈的差分检测算法和带反馈的差分检测算法，带反馈的差分检测算法由于考虑了其它符号对当前符号的影响，其性能相比不带反馈的差分检测算法有一定的提升。文献[5-6]则把差分检测推广到多符号条件下，多符号差分检测算法的性能的虽然有了大幅的提升，但是其算法复杂度也大大增加。文献[7]将差分检测算法与viterbi算法相结合，通过viterbi路径搜索的办法消除符号间的影响，性能相比差分检测算法有很大提升，但是算法复杂度也相对较高。上述差分检测算法的性能提升都是以提高算法复杂度为代价。文中针对GMSK信号的Laurent分解特性，分析传统差分检测算法的基本原理，并提出了基于Laurent分解的差分检测算法，仿真并比较了文中算法与传统差分检测算法的的性能差别。

1 信号模型

1.1 GMSK调制信号

式中，h为调制指数，ai为符号值，取{+1，-1}，T为码元周期，q（t）的表达式为：

式中，g（t）是脉冲成形波形，其表达式为：

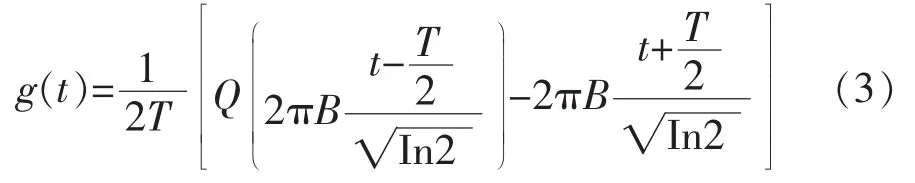
式中B为调制信号带宽。脉冲函数g（t）的长度是无限长的，为了物理可实现，通常把g（t）截短，截短长度为L，从而q（t）重新表示为：

1.2 GMSK信号的Laurent分解形式

GMSK信号是非线性调制信号，非线性调制信号一般可以通过Laurent分解表示为几个线性调制信号的线性叠加的形式。GMSK信号经过Laurent分解后的一般表达式为[8-11]：

式中，Q=2L-1，ck（t）为Laurent分解子波形。bk，i称为Laurent分解后的伪符号，由文献可知GMSK信号经过Laurent分解后，其分解子波形c0（t）的伪符号b0，i的表达式为：

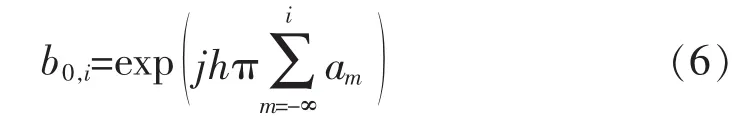
由上式可以看出，相邻两个伪符号进行差分相关后的实部或虚部具有二值性，且其差分相关值与序列值一一对应，其它分解子波形的伪符号则没有这一特性。差分检测算法即利用了此种特性，显然，分解子波形c0（t）的能量在GMSK信号能量中的占比越大，差分检测算法性能越好。图1为不同BT的GMSK信号经过Laurent分解后的子波形c0（t）和c1（t）的波形比较图。

图1 BT值分别为0.1,0.25,0.35,0.5的GMSK信号Laurent分解波形

如图1所示，c0t、c1t分别指lauent分解后的子信号c0（t）、c1（t）。由图可以看出，随着BT值的减小，子波形c0（t）的能量逐渐减小，其在GMSK信号能量中的占比也越来越小。

利用PBL教学模式，可以强化学生的英语学习自信。这主要是由于为了解决既定问题，学生在所处小组内部需要全体发言表达想法，而且在讨论过程中，学生只需要在小组内部表达意见，不会受到教师和所有同学的关注，这时自卑、害怕等各种复杂情绪便会大大缓解，学生也就会开始尝试着去开口说英语。所以，引用PBL教学模式在英语口语教学中是非常有必要的，只有为学生提供更多开口的机会，才能够有效增强学生的自信心。

2 传统差分检测算法

GMSK信号的差分检测的基本原理框图如图2所示[12]。

图2 差分检测原理框图

图2中，所谓差分即为输入信号与其延时N比特后的信号进行相关，信号差分抽样后，再与一特定门限进行比较判决。无论1 bit差分检测还是2 bit差分检测，它们的原理框图都如上图所示，不同的是信号延时和抽样判决时的门限。

当GMSK信号BT值较大时，其信号能量主要集中在分解子信号c0（t）上，可以忽略其它分解子波形的影响，因而信号进行1-bit差分抽样后的表达式可以近似为：

式中，h值为0.5，对差分采样信号d1（k）取虚部操作可知，当Im[d1（k）]=1时，ak=1，当 Im[d1（k）]=-1时，ak=-1，在有噪声条件下，判决方法即为：Im[d1（k）]＞0时，ak=1，当Im[d1（k）]＜0时，ak=1。

同样的，2-bit差分抽样后的表达式可以近似为

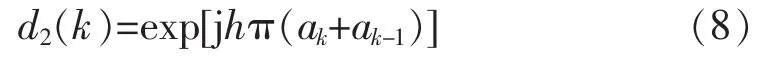
对d2（k）取实部操作可得：

显然2-bit差分采样信号取实部后的值即为输入序列的差分编码序列，因而其判决方法与1-bit差分检测算法相同，将判决得出的序列进行反差分编码即为输入序列。

3 基于Laurent分解的差分检测算法

由上节分析可知，GMSK信号的差分检测算法主要利用了GMSK信号的分解子波形c0（t）的伪符号的特性，而随着GMSK信号BT值的减小，分解子波形c0（t）的能量在GMSK信号中的占比越来越小，其检测性能显然会逐渐降低。为了提高差分检测算法性能，文中提出基于Laurent分解的差分检测算法，首先对接收信号进行Laurent匹配滤波，以降低其它分解子波形对c0（t）的影响，从而提高算法检测性能。

基于Laurent分解的差分检测算法的基本原理框图如图3所示。

图3 基于Laurent分解的差分检测原理框图

图3中，匹配滤波器的冲击响应时间函数为h（t）=c0（-t），匹配滤波后噪声不再是白噪声，因而白化滤波的作用是将匹配滤波器输出的噪声转换为白噪声，以降低噪声对检测算法性能的影响。

进行Laurent匹配滤波后，信号表达式近似表示为

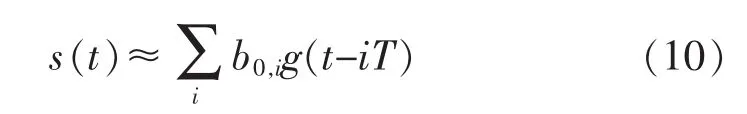
式中，g（t）=c0（t）⊗（-t），其中⊗表示卷积。上式进行抽样后的离散形式可以表示为：

式中，gi=g（t）|t=iT。

由于经过Laurent匹配滤波后的噪声不再是白噪声，因而需对Laurent匹配滤波器的输出信号再进行一次白化滤波操作。令G（z）为gi的z变换，由于g（t）的对称性，有gk=g-k，因而的个根也具有对称性，它可以因式分解成下面形式[13-15]：

接收信号经过白化滤波后的处理及判决方法与上节介绍的传统检测算法相同。显然，本文提出的算法最大的优势就是通过Laurent匹配滤波，最大限度提高具有差分特性的子波形c0（t）在GMSK信号能量中的占比，从而提升算法性能。

4 仿真分析

图4所示为在高斯白噪声条件下，文中算法与传统差分检测算法对不同BT值的GMSK信号的检测误码率曲线。

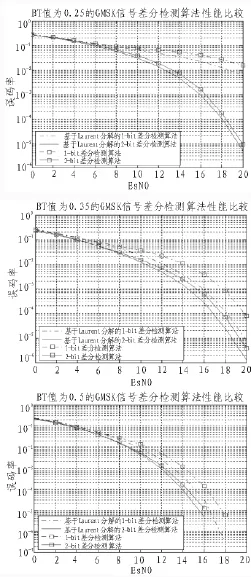
图4 不同BT值的GMSK信号检测误码率曲线

从图4可以看出，随着BT值的减小，文中算法与传统差分检测算法的性能都有大幅下降，这主要是由于具有差分特性的分解波形c0（t）的能量在GMSK信号能量中的占比降低，导致其它分解子波形对算法性能的干扰导致的[16]。当GMSK信号BT值相同时，无论是本文算法还是传统算法，2-bit差分检测算法性能都要优于1-bit差分检测算法性能。同时，由于本文提出的算法首先进行了Laurent匹配滤波，降低了其它分解子波形对算法性能的影响，使得算法性能相比传统差分检测算法有了一定的提升[17]。GMSK信号BT值为0.5，误码率为时，文中算法相比传统算法有近0.5 dB的性噪比增益。

5 结 论

文中从GMSK信号表达式出发，介绍了GSMK信号的一般Laurent形式，由此分析了GMSK信号的差分检测算法的基本原理，并提出了基于Laurent分解的差分检测算法，介绍了算法的基本原理及检测方法。仿真结果表明，误码率为10-5时，文中提出的算法与传统差分检测算法相比有近0.5 dB的信噪比增益，而算法复杂度与传统算法基本相同。

[1]Marvin K Simon，Charles C Wang.Differential detection of Gaussian MSK in a mobile radio environment[J].IEEE Trans.On Vehicular technology，1984，33（4）:307-320.

[2]王茂磊，张志恒，蔡凡.卫星通信中的GMSK信号的解调算法研究 [J].中国科学院上海天文台年刊，2012（33）:114-120.

[3]Yongacoglu A，Makrakis D，Feher Kamilo.Differential detection of GMSK using decision feedback[J]. IEEE Trans.On Communication，1988，36（6）: 641-649.

[4]卫洪春，姜凯.带判决反馈的GMSK差分解调算法研究与实现[J].现代电子技术，2014，37（17）:1-4.

[5]Abrardo A，Benelli G，Gao G.Multiple-symbols differential detection of GMSK[J].IEEE Electronics Letters，1993，29（25）:2167-2168.

[6]Chunjun Gao，Alexander M.Haimovich，Debang Lao.Multiple-symboldifferentialdetection for MPSK space-time block codes:decision metri and performance analysis[J].IEEE Trans.On communication，2006，54（8）:1502-1510.

[7]吴团峰.基于2比特差分的GMSK信号解调算法[J].军事通信技术，2002，23（1）:35-40.

[8]王聪，朱守中，姜利文，等.基于laurent分解的星载AIS解调算法[J].飞行器测控学报，2012，31（5）: 40-44.

[9]Proakis J.数字通信 [M].5版.北京：电子工业出版社，2011.

[10]Umberto Mengali，Michele Morelli.Decompasition of M-ary CPM signals into PAM waveform[J]. IEEE Trans.On information theory，1995，41（5）: 1265-1275

[11]Laurent P A.Exact and approximate construction of digital phase modulations by superstition of amplitude modulated pulses [J].IEEE Trans.On communication，1986，34（2）:150-160.

[12]董诗韬.同信道干扰下AIS信号非相干解调技术研究 [D].南京：南京理工大学，2012.

[13]Giulio Colavolpe，Riccardo Raheli.Noncoherent sequence detection of countinuous phase modulations[C]//IEEE Global Telecommunication Conference.1998，1:556-561

[14]Fonseka JP.Noncoherent detection with Viterbi decoding for GMSK signals[J].IEEE Proceedings-Communication，2002，143960:373-379.

[15]David G，Forney J R.Maximum-likelihood sequence estimation of digital sequence in the presense of intersymbol interference[J].IEEE Trans.on Information Theory，1972，18（3）:363-378.

[16]张骞，邵宝杭.一种基于软件无线电思想的GMSK调制设计[J].电子设计工程，2012（19）：151-153.

[17]崔学超.基于减背景和混合差分的运动目标检测算法[J].电子科技，2010（10）：85-88.

An improved method for differential detection of GMSK

ZHU Xiao-feng，WANG Wei
（China Academy of Space Technology（Xi'an）,Xi'an 710100，China）

Traditional differential detection of GMSK is improved by a new method based on decomposition with Laurent method,this new method added Laurent match filter and whitening filter,it reduced the impact of other sub waveforms after decomposing.The simulation shows the advantage of this new method,when bit error rate is,the new method have about 0.5 dB signal to noise ration gain compared with the traditional method,and its complexity is increasing little.

GMSK modulate；decomposition with Laurent method；differential detection；whitening filter

TN92

：A

：1674－6236（2017）03-0089-04

2016-02-02稿件编号：201602005

朱晓峰（1988—），男，湖北黄冈人，硕士研究生。研究方向：卫星通信。