基于视觉导航的动态航迹优化

吴成良，曹云峰，庄丽葵，谢 也，丁 萌

（1.南京航空航天大学 自动化学院，江苏 南京210000；2.南京航空航天大学 航天学院，江苏 南京210000；3.南京航空航天大学 民航学院，江苏 南京210000）

基于视觉导航的动态航迹优化

吴成良1，曹云峰2，庄丽葵2，谢 也1，丁 萌3

（1.南京航空航天大学 自动化学院，江苏 南京210000；2.南京航空航天大学 航天学院，江苏 南京210000；3.南京航空航天大学 民航学院，江苏 南京210000）

针对基于视觉导航的航迹规划技术存在的两个问题：第一，作为一类存在有限测量量程的导航系统，视觉导航系统需要目标始终出现在摄像头的视野内；第二，当目标始终在摄像头的光轴延长线附近时，视觉算法能够更有效率并且更准确的解决位姿估计问题；文中首先将航迹优化问题转化为最优控制问题，结合飞行器运动动力学特性，设计最优控制问题的约束与最优指标。然后，文中利用伪谱法将连续时间最优控制问题转化为离散时间非线性规划问题，并在此基础上研究了基于滚动时域的动态规划方法，最终减少视觉导航误差对航迹优化的不良影响。

视觉导航；最优控制；动态规划；Gauss伪谱法；滚动时域

基于视觉导航的无人机自主飞行主要是利用装配在无人机上的摄像头获得着陆场附近的图像，并采用视觉技术估计无人机位置和姿态信息，同时感知着陆场周围环境，辅助无人机完成自主飞行。基于视觉导航作为一种完全自主的导航方式，并不依赖于其他的地面和空中设备，故在提高无人机自主性方面有着很大的优越性[1]。相比于传统的INS/GPS等导航方式，视觉导航因完全自主且无源等特点得到了广泛而深入研究，但基于视觉导航的航迹规划技术仍然存在很大的研究发展空间。

与传统的导引问题相比，基于视觉的导引方式虽然可以获得导航系统直接提供的无人机与目标之间的相对位姿关系，但由于视觉导航的探测范围有限（如摄像头视野限制），故规划的航迹必须始终保证目标出现在视觉导航系统的探测范围内 （如摄像头视野内）。另外，基于图像特征的视觉算法的实时性和准确性很强烈的依赖于特征在图像中的位置以及表现形式，故导引算法如何引导无人机（摄像头）在完成任务的同时始终保持有利于视觉算法的位姿，也是一个亟待解决的问题。

Rolf Rysdyk[2]通过保持无人机纵轴线与目标视线之间的相对角度来实现对目标的持续跟踪，并以此确定无人机的几何路径。文献[3]和[4]在仅考虑平面位置与方位的情况下，分别利用解析法和穷举法解算出符合要求的航路点。上述文献在基于视觉的路径规划方面很有借鉴意义，但仍停留在几何路径规划上，未涉及无人机本身的运动动力学约束。在考虑无人机动力学特性的航迹规划中，基于最优控制理念的航迹优化算法由于能将多种约束以及最优指标同时结合，受到了广泛的关注。近十年来，发展最迅速的最优控制问题求解方法属伪谱法，其已经成功应用在无人机的众多领域，例如高超声速飞行器的航迹最优与制导[5]、协同作战[6]、航天器姿态最优[7]等。另外，目前很少有学者将视觉系统的特点与航迹优化问题相结合，其中Geiger[8]将视觉传感器所覆盖目标的范围作为性能指标，利用直接配点法完成了最优航迹的设计。但文献未考虑有限视场的约束，故仍可能出现目标丢失的情况，同时因为摄像头特殊的安装方式，其性能指标仅适用于二维情况。

与传统的航迹规划问题相比，基于视觉的航迹规划技术的关键问题主要体现在两个方面：第一，作为一类存在有限测量量程的导航系统，视觉导航系统需要目标始终出现在摄像头的视野内；第二，当目标始终在摄像头的光轴延长线附近，即出现在图像中心周围时，视觉算法能够更有效率并且更准确的解决位姿估计问题。文中首先将航迹优化问题转化为最优控制问题，并针对上述的技术难点，结合飞行器运动动力学特性，设计最优控制问题的约束与最优指标。然后，文中利用伪谱法将连续时间最优控制问题转化为离散时间非线性规划问题，并在此基础上研究了基于滚动时域的动态规划方法，以期减少视觉导航误差对航迹优化的不良影响。

1 航迹约束与最优指标

1.1 飞行器约束

一般来说，无人机的航迹可以由其三维位置信息唯一确定。根据质点运动在惯性坐标系和航迹坐标系下的关系，可以得到无人机的运动学方程[9]。

其中（x，y，z）为无人机亦即摄像头在着陆坐标系下的位置，在航迹规划中通常使用高度值h=-z代替Opzp轴上的坐标值。同理，（V，γ，χ）也分别为相对于着陆坐标系的飞行速度、航迹角和航向角。

为减少优化算法的计算量，仅考虑无人机的部分动力学约束，并且假设无人机做无侧滑飞行，同时忽略侧力，可得其在航迹坐标系下的动力学方程。

其中α，φ分别代表迎角和滚转角；（T，L，D）分别为无人机所受推力、升力和阻力，其表达式如下[10]：

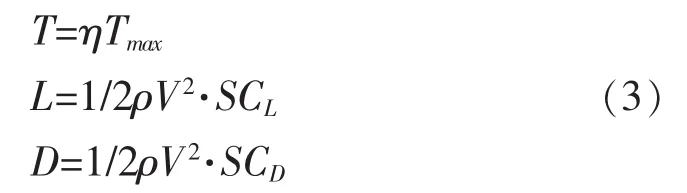
其中Tmax为最大推力；S是参考翼面面积；（ρ，CL，CD）分别为大气密度、升阻力系数，具体表达式如下：

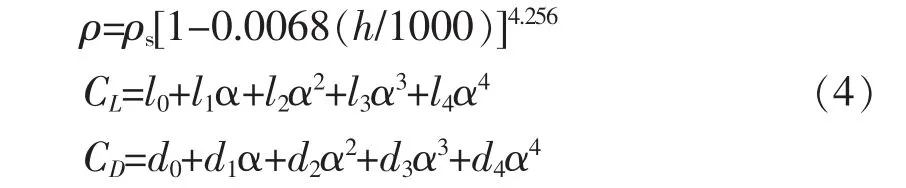
其中ρs为海平面的大气密度；而l，d为随迎角变化的系数。

综上所述，航迹优化的变量可转化为过程约束中的状态变量x=（x，y，h，V，γ，χ）T和虚拟控制输入[11]u=（η，α，φ）T。

1.2 基于视觉导航的约束与最优指标

依据视觉导航的特点，本文结合了目标在视场内/目标在视场中间的航迹约束和最优指标理念。基于目标在视场内的航迹约束可以有效保证目标出现在摄像头的测量范围内，降低甚至杜绝跑道跟踪过程中的目标丢失情况；基于目标在视场中间的思想则以目标出现在视场中间为最优指标，旨在保持无人机处于有利于视觉算法的位姿，从而减小视觉算法的计算量，提高测量算法的速度和精度。目标在视场内即是要求光轴rLOS在视场范围内，而目标在视场中间则是要求rLOS与目标视线rOA重合。

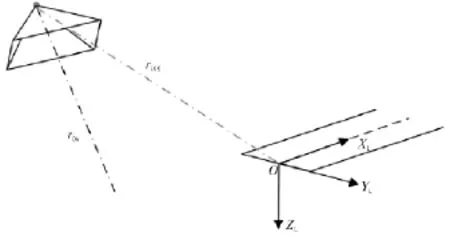
图1 3D视场与视线

图1中向量γLOS与γOA的表达式如下：

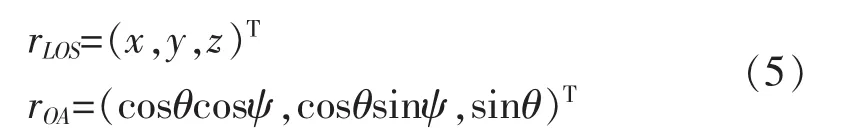
由此，航迹约束和最优指标可转化为：

注意到上文所构建的航迹约束和最优指标中均包含欧拉角（φ，θ，ψ），然而航迹优化的变量并不包括所有的欧拉角，故需要通过着陆坐标系、机体坐标系和航迹坐标系之间的旋转关系求出缺省欧拉角或其三角函数表达式[12]。根据着陆坐标系和机体坐标系之间的关系易得：

若将公式（8）展开

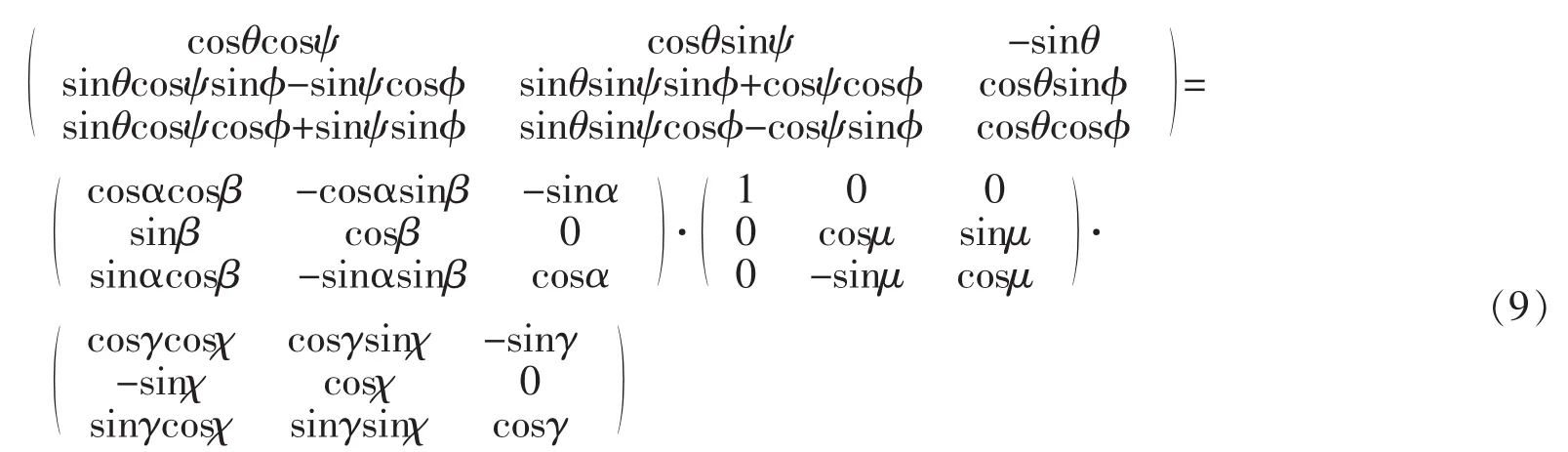
其中μ为航迹滚转角。

2 基于伪谱法的动态航迹优化

2.1 Gauss伪谱法

常见的伪谱法包括Chebyshev伪谱法（CPM）、Legendre伪谱法 （LPM）、Gauss伪谱法 （GPM）和Radau伪谱法（RPM）等，各种伪谱法所选取的插值基函数、配点类型都不尽相同。其中GPM因高效性与实时性被广泛应用在实际的机载航迹规划系统中[13]。GPM的基本思想是：先将状态量和控制量在配置点进行离散化，并利用Lagrange多项式来逼近真值，通过对插值多项式进行求导和积分等运算来替代原来的性能指标、微分方程与约束，最终将最优控制问题转换为NLP问题。本文的GPM选取的离散点（除端点）是阶Legendre多项式微分的零点，即所谓的Legendre-Gauss（LG）配点[14]。虽然随着配置点的增加，LG配点的收敛效果并不如 Legendre-Gauss-Lobatto（LGL）等方法，但在较少配置点的情况下，LG配点却能表现出优于他法的性能[15]。

LG配点本质上是一种非等间距的Gauss离散点，故其可以更好地逼近真值，并且能有效地减小Runge现象[16]。阶Legendre多项式的表达式为：

通过PN（τ）的一阶导数的零点可以得到N个时间配点，记为τi，i=1，…，N，若再加上初始时刻τ0=-1和终端时刻τf=τN+1=1，则可以在τ∈[-1，1]范围内得到N+2个节点τi，i=0，1，…，N，N+1。

特别的，GPM并不直接对终端时间的状态量离散化[17]，而是将状态量和控制量分别在[-1，1）和（-1，1）区间内离散化

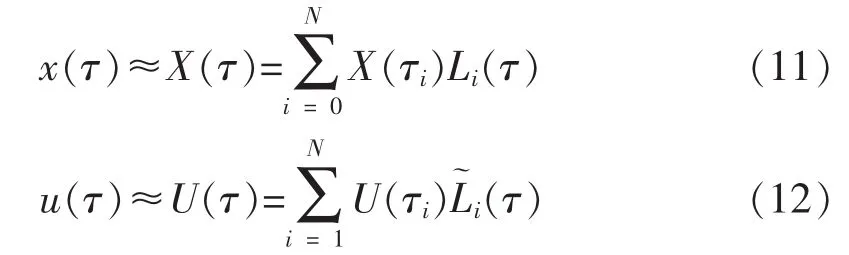
其中Li（τ）和（τ）即是Lagrange多项式，定义如下：

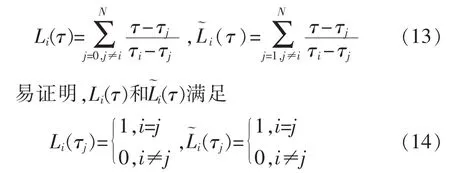
显然，利用Lagrange多项式来离散原来的连续函数可以保证配点处的近似值等于真值。另外，状态量和控制量可以使用不同的Lagrange基函数以及不同数量的LG配点。

2.2 基于滚动时域的动态规划

对于光滑问题，Gauss伪谱法因为以全局插值多项式为Lagrange多项式基函数，可以拥有全局最优的能力。相较于局部最优法，全局法因较少的参数和优化次数可以获得更高效的规划。但针对基于视觉的航迹优化，全局法存在一定的局限性。一般来说，当刚完成目标识别时，由于先验知识有限，基于视觉的位姿估计可能会产生较大误差。假设在航迹优化初始点视觉位姿估计算法的误差较大，则基于GPM的规划航迹可能较大的偏离了真实的最优航迹，如此基于像素坐标系航迹优化的意义也减少了很多。因此，文中研究了基于滚动时域 （Receding Horizon Control，RHC）的航迹更新方法。

RHC并不是一个全新的航迹规划方法，它只是将全局最优问题转换为局部的有限时间片最优问题，或者说是随着时间的推移将Dubins和GPM反复滚动实行。一般的RHC仅关注单一时间片内的优化[18-19]，这样的优化方式突出了RHC的特色，但也大大增加了规划的计算量，这是本文所不希望看见的，故本文利用多个时间片同步优化的方法。文中所设计的滚动过程可表述如下：

a）利用K个等分点将全局时间[t0，tf]分成K+1段，总共得到K+2个节点ti，i=0，1，…，K，K+1；

b）初始时刻t0，将t0，t1，t2合成一个优化时间片[ξ0，ξ1]，在[ξ0，ξ1]上配置N个LG配点，得到N+2个节点τk，k=0，1，…，N，N+1，并上利用三维Dubins航迹规划算法估计节点的初值；

c）任意时刻ti，i=1， …，K-1将ti，ti+1，ti+2合成一个优化时间片[ξ3i，ξ3i+1]，在[ξ3i，ξ3i+1]上配置N个LG配点，得到N+2个节点τk，k=0，1，…，N，N+1，其中τk∈[ti，ti+1]的初值估计利用上一次GPM的优化结果，而τk∈[ti+1，ti+2]利用三维Dubins估计初值；

d）终止时刻tK，tK+1，停止时域滚动。这样，本文将全局的航迹优化转化为滚动更新的一系列有限时间片局部优化问题，其中每次更新的时间片长度、配点数目和优化模型等都相同，仅有初始值不同。

3 仿真结果分析

一般来说，当刚完成目标识别时，由于先验知识有限，基于视觉的位姿估计可能会产生较大误差。假设在航迹优化初始点视觉位姿估计算法的误差较大，则基于G/Dubins-P的规划航迹可能较大的偏离了真实的最优航迹，本文通过在初始点引入位姿估计误差，验证基于G/D-RHC-P航迹更新的优势。

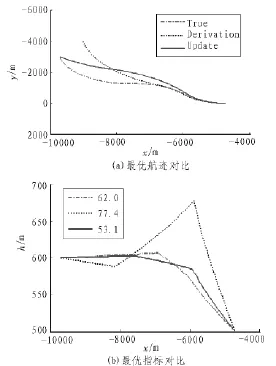
图2 G/Dubins-P和G/D-RHC-P的最优航迹比较

图2所示为初始点存在较大位置估计误差时，G/D-RHC-P算法规划的最优航迹：设定无人机初始点为（-8 700，-3 000，600）m。假定因为位置估计误差航迹规划初始点变为（-8 000，-4 000，600）m。其中基于真实位置的最优航迹为True，基于偏离位置的规划航迹为Derivation，而利用航迹更新动态修正的航迹为Update，另外（b）图中的数字表示不同规划航迹的最优指标。从图中可以看出，规划后的航迹明显偏离了真实的最优航迹，若无人机着陆过程中一直跟踪错误的航迹，虽然也可以顺利到达截获点，但此时基于像素坐标系的指标不能达到最优，且有可能因为过大的跟踪偏差给飞行控制器带来不必要的负担。

4 结束语

文中提出了目标在视场内/目标在视场中间的航迹约束和最优指标，结合GPM有效保证了目标出现在摄像头的测量范围内，从而降低甚至杜绝了跑道跟踪过程中的目标丢失情况。同时，当刚完成目标识别时，基于视觉的位置估计可能会产生较大误差，故本文研究了基于RHC的航迹更新方法实现了动态优化，有效解决了最优航迹偏离问题。

[1]Stepanyan V.Vision based guidance and flight control in problems of aerial tracking[D].Virginia Polytechnic Institute and State University，2006.

[2]Yoon S，Kim H J，Kim Y.Spiral landing guidance law design for unmanned aerial vehicle net-recovery[J]. Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，2010，224（10）:1081-1096.

[3]Ceccarelli N，Enright J J，Frazzoli E，et al.Micro UAV path planning for reconnaissance in wind[A]. In American Control Conference[C]//New York: IEEE，2007:5310-5315.

[4]Hanson C，Richardson J，Girard A.Path planning of a Dubins vehicle for sequential target observation with ranged sensors，In American Control Conference[C]//San Francisco:IEEE，2011:1698-1703.

[5]Jorris T R，Cobb R G.Three-Dimensional trajectory optimization satisfying waypoint and no-fly Zone constraints[J].Journal of Guidance，Control and Dynamics，2009，32（2）:551-572.

[6]Huntington G T，Rao A V.Optimal spacecraft formation configuration using a Gauss pseudospectral method[C]//In Proceedings of the 2005 AAS/AISSSpaceflightMechanics Meeting，Colorado，2005：1-6.

[7]Kang W，Bedrossian N.Pseudospectral optimal control theory makes debut flight，Saves NASA $1M in Under 3 Hours[J].SIAM News，2007，40（7）:1-5.

[8]Geiger R B，Horn F J，DeLullo M A，et al. Optimalpath planningofUAVsusingdirect collocation with nonlinear programming[J].Guidance，Control and Dynamics Conference，2006: 2006-6199.

[9]Horie K，Conway B A.Optimization for fighter aircraft vertical-plane maneuvering using poststall flight[J].Journal of aircraft，2000，37（6）:1017-1021.

[10]Khademi I，Maleki B，Mood A N.Optimal three dimensional Terrain Following/Terrain Avoidance for aircraft using direct transcription method[A].In Mediterranean Conference on Control&Automation[C]//Corfu:IEEE，2011：254-258.

[11]Sharma T，Williams P，Bil C，et al.Optimal three dimensional aircraft terrain following and collision avoidance[J].ANZIAM Journal，2007（47）:695-711.

[12]程建锋，董新民，薛建平，谭雪芹.基于Gauss伪谱法的飞机最优目标瞄准控制 [J].计算机应用，2013，33（11）：3291-3295.

[13]Ross I M，Fahroo F.Issues in the real-time computation of optimal control[J].Mathematical and Computer Modeling.2006，43（9-10）:1172-1188.

[14]Williams P.A Gauss--Lobatto quadrature method for solving optimal control problems[J].ANZIAM Journal，2006（47）:101-115.

[15]Huntington G T.Advancement and analysis of a Gauss pseudospectraltranscription foroptimal control problems[D].University of Florida，2007.

[16]孙勇.基于改进Gauss伪谱法的高超声速飞行器轨迹优化与制导 [D].哈尔滨：哈尔滨工业大学，2012.

[17]Benson D A，Huntington G T，Thorvaldsen T P，et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J]. Journal of Guidance， Control， and Dynamics，2006，29（6）:1435-1440.

[18]俞利新，来强，曲大鹏.基于威胁规避的战斗机网络瞄准攻击引导轨迹优化 [J].空军工程大学学报：自然科学版，2014，15（1）：38-42.

[19]俞华军.带有非线性扰动的不确定时滞系统鲁棒预测控制[J].电子设计工程，201（6）：190-193.

Dynamic route optimization based on visual navigation

WU Cheng-liang1，CAO Yun-feng2，ZHUANG Li-kui2，XIE Ye1，DING Meng3
（1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210000，China；2.College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210000，China；3.College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 210000，China）

As to the two key problems of path planning technology based on vision navigation:first，as a kind of limited measuring range navigation system，the visual navigation system requires that target should be in the camera view；Second，it is more efficient and accurate for visual algorithm to solve The pose estimation problem when the target is always near the optical axis of camera extension cord.Route optimization problem is firstly transformed into the optimal control problem in this paper and the optimal control problem of constraint and optimal index is designed by combining with the aircraft motion dynamics characteristics.Then，continuous time optimal control problem is transformed into discrete time nonlinear programming problem by utilizing the method of pseudo-spectral.While the dynamic planning based on rolling time domain method is researched to reduce the bad influence of visual navigation error on route optimization.

visual navigation；optimum control；dynamic planning；Gauss pseudo-spectral；rolling time domain

TP39

：A

：1674－6236（2017）03-0014-05

2015-12-30稿件编号：201512317

吴成良（1991—），男，河南商丘人，硕士。研究方向：导航、制导与控制。