空中爆炸冲击波作用的数值仿真实验研究

张如林, 程旭东, 张艳美, 贾娟娟,2

(1. 中国石油大学(华东) 储运与建筑工程学院, 山东 青岛 266580；2. 中国移动通信集团山东有限公司青岛分公司, 山东 青岛 266000)

空中爆炸冲击波作用的数值仿真实验研究

张如林1, 程旭东1, 张艳美1, 贾娟娟1,2

(1. 中国石油大学(华东) 储运与建筑工程学院, 山东 青岛 266580；2. 中国移动通信集团山东有限公司青岛分公司, 山东 青岛 266000)

研究了爆炸冲击波作用的数值仿真实验方法,分析了用经验公式计算冲击波超压峰值的差异及其原因。基于LS-DYNA软件、ALE算法和流固耦合理论建立了爆炸冲击波的数值实验方法,并将数值实验结果与爆破现场试验数据、经验公式计算结果进行对比,验证了数值仿真实验技术的有效性。分析了LNG储罐的爆炸冲击响应和冲击波超孔压响应,得到冲击波遇到储罐结构后的绕射过程。实验表明:爆炸荷载数值实验方法可用于大型LNG储罐工程的抗爆问题研究。

爆炸冲击波； 数值仿真实验； ALE算法； LNG储罐

土木工程问题的研究方法主要有3种:理论研究、试验研究和数值计算[1]。理论研究一般只针对少数规则、简单的问题,通过理论分析求出解析解,适用范围有限；试验研究一般通过模型试验或现场试验的方法,但是物理模型试验往往成本高、周期长,且模型参数难以调整,而现场试验的运行成本高,很多大型试验属于破坏性试验,重复性差。数值计算也称为数值实验,通过计算机仿真研究实际工程问题。数值实验可以模拟工程情况,形象地展示结构的变形和破坏规律,对于复杂问题也可以较好地处理。另外,通过数值实验还可以得到许多在常规实验室实验中难以观测的重要信息,具有成本低、通用性强、灵活方便、可重复性好等特点,因此应用范围比较广。随着计算机的发展,计算机辅助教学手段逐步完善,数值实验已成为工程问题物理实验教学的重要补充手段[2-3]。

为此,笔者引入数值实验技术,开设了“土木工程分析软件与应用”课程,以提高学生的数值实验应用能力和科研水平。作为石油行业院校的土木工程专业,除了研究常规的土木工程问题,也侧重于与石油相关的土木工程问题(如储油罐、输油管道、盐岩地下储气库等)的解决。本文通过研究空中爆炸冲击波的数值仿真实验技术,为研究大型LNG储罐在爆炸荷载下的冲击响应问题奠定基础。

LNG储罐是存储液化天然气的重要设施,其安全性至关重要,如有液化天然气泄漏,可能引起火灾、爆炸等重大事故。1984年,墨西哥国家石油公司的LPG储运站因管线破裂、气体泄漏造成15个储罐连续爆炸[4]。爆炸冲击波在空气中的传播属于流固耦合问题,对爆炸荷载作用下LNG储罐的冲击破坏问题难以用现场爆炸实验方法研究,需要借助数值仿真实验方法完成。本文基于LS-DYNA软件,采用ALE算法和流固耦合理论探讨合理的建模方式,建立空气中爆炸冲击波的数值仿真实验方法,进而分析爆炸荷载作用下LNG储罐的冲击响应。

1 爆炸冲击波实验及超孔压峰值经验公式

1.1 爆炸冲击波荷载的物理试验

评价燃料空气炸药(fuel air explosives,FAE)爆炸威力的一个重要参数是爆炸冲击波超压。大多数研究是通过TNT现场标定的方法评价FAE的爆炸威力,即根据实测的FAE爆炸冲击波参数与TNT爆炸冲击波参数进行比较,分别求出各对应点的等效TNT装药量,从而求出该FAE的爆炸威力的TNT当量比,并进行威力评价。因此,TNT爆炸冲击波参数的测量非常重要。目前,关于爆炸冲击波的现场试验研究开展较多[5-10],试验所得实测值可以作为数值仿真实验结果的对比依据。

在对FAE类武器进行试验与威力评价时,需首先在同一试验场地对TNT炸药的爆轰参数进行准确标定。以文献[6]中的实验方法为例,该实验场地选择平坦地面,TNT药柱的支架高度H=1.2 m。沿爆源一侧设置互相垂直的两路地面压力传感器。为了提高测试精度,每路主力线安装两组地面压力传感器,每组布设8个测点(见图1)。

图1 实验场及传感器场地布置图

该实验采用多通道数据采集仪进行现场测量,仪器的主要性能指标为:信号输入电压范围0～-5 V；采样频率100 kHz～1 MHz；预制采样点数为16 kB、32 kB、64 kB；放大倍数10～100倍；分辨率8 bit。

1.2 爆炸冲击波传播规律

爆炸是物质状态的突然物理或化学变化,期间伴随着能量的释放。TNT炸药在空气中爆炸时,会形成一团瞬间占据炸药原有空间的高温、高压气体,继而猛烈推动周围静止的空气,同时产生一系列的压缩波向四周传播,压缩波最终叠加成冲击波。自由空气中的理想冲击波波形即压力时程曲线如图2所示。

图2 自由空气中理想压力时程曲线

冲击波压力、超压峰值、冲量、持续时间等冲击波参数用来描述TNT爆炸产生的入射冲击波的传播规律,而冲击波的各种参数常通过比例距离来表达:

1.3 爆炸冲击波超压峰值经验公式

图3 冲击波超压峰值随比例距离的变化结果对比

从图3可知,当比例距离为0.1～1.0 m·kg-1/3时,各经验公式结果总体变化趋势基本一致,随着比例距离的增大,超压峰值由于能量耗散而逐渐衰减,采用Henrych和Baker公式得到的超压峰值较低,其他的则较高。这些文献大多为早期研究,属于高爆炸药冲击波范围。当比例距离为0.1 m·kg-1/3时,各经验公式计算的最大值和最小值分别为1761.68 MPa 和35.46 MPa,相差近50倍,与平均值660.27 MPa相对误差分别为-62.5%和94.6%,波动较大。当比例距离为1.0～10 m·kg-1/3时,随着比例距离的增大,超压峰值继续衰减,相互之间的误差逐渐减小。当比例距离为1.0 m·kg-1/3时,各经验公式的平均值为1.03 MPa,而最大值和最小值分别为1.94 MPa 和0.80 MPa,相对误差减小到-46.9%和22.3%。

可见,早期研究的冲击波超压普遍低于各经验公式的平均值。若采用常用的经验公式估算冲击波超压,容易产生误差,可能低估爆炸威力,降低计算结果的安全性。

为便于与数值仿真结果比较,将图3中各经验公式计算结果进行加权平均得到平均值,冲击波超压平均值函数化表达式为

2 爆炸冲击波传播过程的数值实验方法

利用LS-DYNA软件中的ALE算法对空中爆炸冲击波的传播进行数值仿真实验。在该算法中,对空气采用ALE网格,对炸药定义为流体,既可以通过多物质单元来实现流固耦合的动态分析,又可使材料物质在网格中流动,避免爆炸过程中网格的过分畸变引起的数值计算困难,甚至导致计算结果的不稳定。

2.1 炸药建模方式

在LS-DYNA软件中有两种施加爆炸荷载的方法:一种是把爆炸冲击荷载简化成三角形冲击波压力时程曲线(见图2),另一种是建立炸药单元模拟爆炸过程。前者能有效减少计算时间,但只适用于球形炸药,不能反映冲击波作用对结构各部分的压力。本文采用后者,虽然能解决荷载简化不足的问题,但会涉及较大范围的空气部分,计算量较大。

建模时采用ALE技术,即爆炸单元和空气采用ALE单元,通过关键字*ALE-MULTI-MATERIAL_GROUP定义ALE网格。网格中包含多种物质,这样就能实现空间网格中物质和能量的传输；和关键字*INITIAL_VOLUME_FRACTION_GEOMETRY结合使用,在空气单元中定义炸药,空气中的一部分被定义成炸药的材料属性。通过该关键字也便于改变炸药的半径和形状,并且空气的网格划分更加方便。使用Lagrange单元定义被爆炸结构,炸药和结构之间通过定义PART间的耦合实现爆炸过程的仿真。该方法解决了网格畸变过大引起的计算发散、计算结果不可信等问题。

本文采用ALE技术模拟爆炸冲击波的传播过程以及爆炸荷载对结构的冲击作用，建好的炸药和空气的相对位置平面示意图如图4所示。

图4 炸药和空气平面示意图

2.2 材料模型的确定

对于炸药材料模型,一般采用JWL 状态方程描述压力与体积的变化,反映炸药爆炸产生的压力与相对体积的关系,其表达式为

式中,p为爆轰压力；E0为炸药单位体积的初始内能；V为炸药的相对体积,A,B,R1,R2和ω为材料参数。

使用*MAT-HIGH-EXPLOSIVE-BURN定义炸药,各参数取值如表1。

表1 JWL状态方程及炸药模型参数

空气采用MAT_NULL材料模型。LS-DYNA程序中采用理想气体线性多项式状态方程描述,通过设置关键字*EOS_LINEAR_POLYNOMIAL中的参数来描述,表达式为

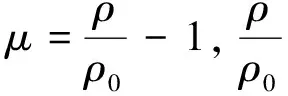
式中,p为空气压力,γ为气体的比热比,ρ为空气的现时密度,ρ0为初始密度,E0为单位体积初始内能。

2.3 可靠性验证

为验证本文数值仿真实验方法的合理性,将模拟结果、经验公式计算结果以及爆炸现场试验实测结果[5-10]进行比较。在进行数值实验时,通过改变炸药质量和测试点与爆心的距离来改变比例距离的值,共有24种工况。

以炸药质量为6 600 kg、持续时间0.3 s为例,给出6个典型时刻爆炸超压云图如图5所示。炸药爆炸后,爆轰波会在极短的时间内从起爆点迅速传播到整个炸药。爆轰过程完成后,原本固态炸药转变为能量极高的高温高压气体,以冲击波的方式向外传播。波振面上的超压最大,符合经验结果和相关的物理定律。

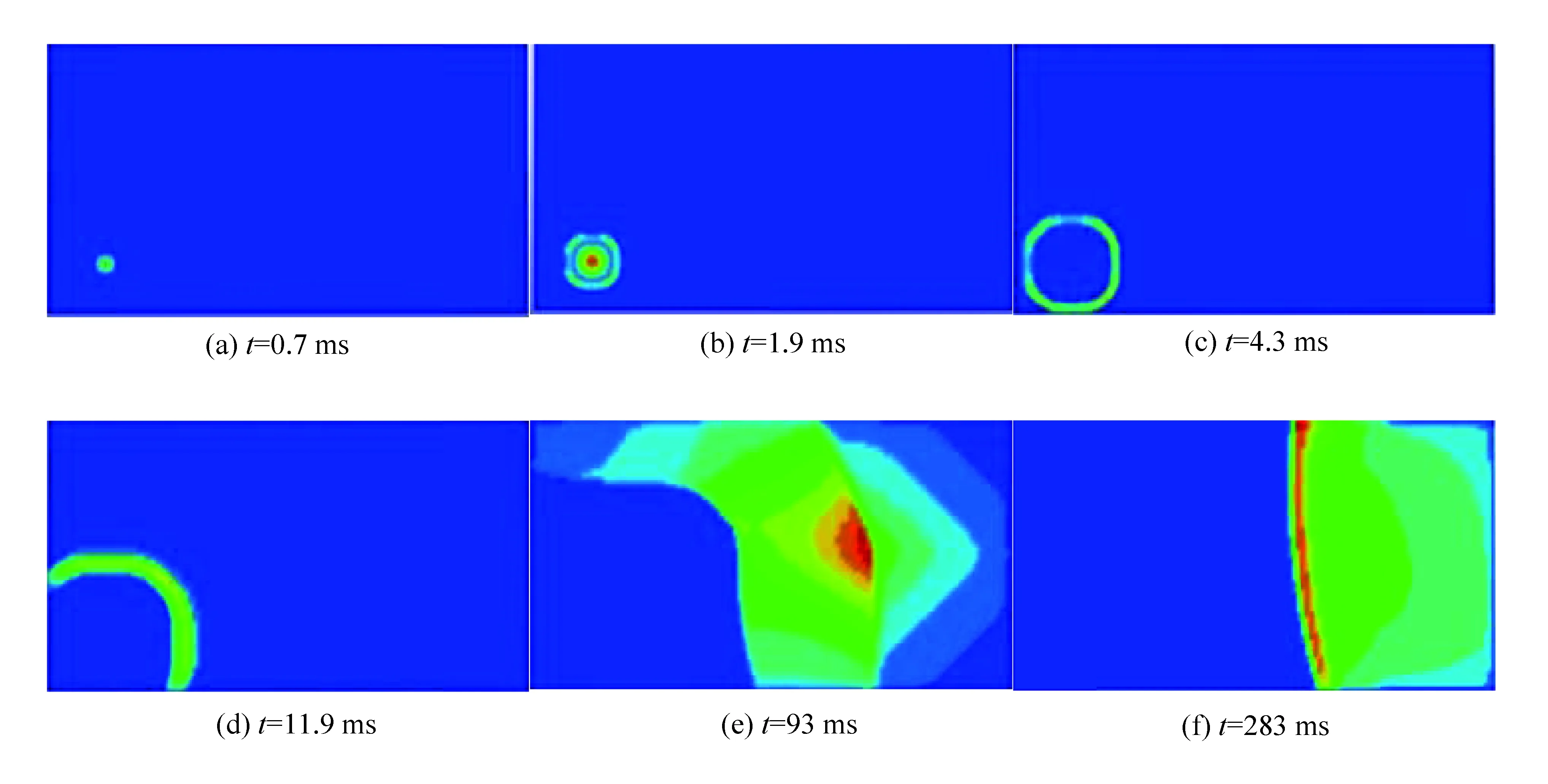
图5 爆炸冲击波的传播过程

研究爆炸冲击波超压峰值随着距离或爆炸药量的变化关系,得到超压峰值随比例距离的变化趋势如图6所示,并与平均公式所得进行比较。

图6 不同方法得到的超压峰值-比例距离曲线对比

从图6可以看出，通过数值仿真实验得到的超压峰值随比例距离的变化趋势,该趋势与经验公式平均值以及现场试验实测结果的变化趋势基本一致,都是随着比例距离的增大而减小。当比例距离为0.1～1.0 m·kg-1/3时,数值仿真实验得到的超压峰值稍小于平均值。主要原因是比例距离越小,距离爆源越近,爆炸场情况越复杂,马赫反射造成的影响会更加显著[6]。由于超压峰值本身的离散性和在近爆区作用持续时间短的特性,无论是现场试验还是数值仿真实验都难以精准地确定近爆区超压峰值,同时试验所处环境以及一些人为因素也对会对精度有一定的影响,并且在数值仿真实验中,网格大小等因素也会有所影响。

随着比例距离的增大,爆炸荷载产生的冲击波超压峰值减小,数值结果和平均值逐渐接近。经验公式主要适用于自由场中的冲击波压力场计算,未考虑到地面反射冲击波的能量加强作用,因此经验公式结果一般小于实测结果，爆破实测值离散性较大；而数值仿真实验结果大多介于试验实测值的上限值和下限值之间。当比例距离接近5时,数值仿真实验结果比实测值和经验公式平均值有所减小。

总体来看,数值仿真实验结果和经验公式计算值和爆破试验实测值比较接近,说明数值实验技术是可行的。

3 数值实验技术在LNG储罐抗爆研究中的应用

3.1 LNG储罐数值分析模型的建立

设置了LNG储罐结构参数。混凝土外罐强度等级为C50,内径82 m,壁厚度0.8 m,高40 m；混凝土球面穹顶外径82.4 m,内径82 m,边缘厚0.8 m,顶部厚0.4 m；预应力钢筋选用7股钢绞线,公称直径15.7 mm。内罐采用9%的镍合金钢,钢板的厚度12～36 mm。依据GB50316—2000《工业金属管道设计规范》,设管道泄漏后爆炸点距地面10 m,与储罐距离亦为10 m。空气域形状选为矩形,尺寸为110 m×100 m×60 m,能完全覆盖储罐。储罐底部采取全部固定约束。选取混凝土外罐壁上3个特征点进行研究,分别为正对炸药的迎爆面中心点A(距罐底高10 m),与A相对的背爆面中心点B以及侧爆面点C,如图7所示。

图7 LNG储罐爆炸计算模型示意图

选择低压输送管道泄漏为泄漏源,假设出现管道小孔泄漏,孔径为20 mm,计算时间取100 s。根据文献[14]取泄漏速率为7.6 kg/s,经过100 s泄漏量为760 kg。设泄漏的天然气中参与爆炸的蒸气云占总体积的30%,计算TNT当量的公式为

式中,mTNT为TNT当量,kg；α为蒸汽云中TNT当量系数,取0.04；mr为蒸气云中燃料的总质量,kg；Qr为燃料的燃烧热,kJ/kg；QTNT为TNT的爆炸热,取4.52 MJ/kg；爆炸发生在地面时,b取1。计算得到TNT炸药当量为200 kg,密度为1 580 kg/m3,半径为0.3 m。

3.2 爆炸冲击响应结果分析

根据数值仿真实验结果,选取3个典型时刻的爆炸冲击波膨胀及传播过程如图8所示。

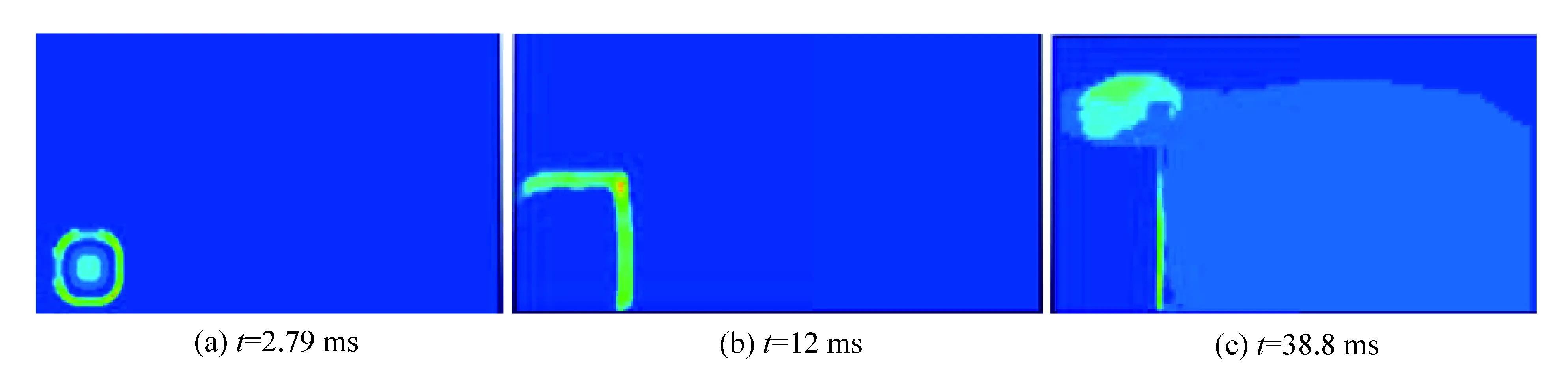
图8 爆炸冲击波膨胀及传播过程

根据图8可知,当冲击波遇到罐体后,高速气流向前运动受到阻碍,下一层气流的运动也受到抑制,在结构附近形成高压区,波阵面前方的压力大于后方的压力,未受到阻挡的冲击波沿外罐壁继续前进。随后高压区上移,在高压区气体向低压区流动时,稀疏波也会向高压区流动。在气体流动过程中,由于外罐侧面和穹顶处受到入射冲击波波后气流的影响,气体的运动方向发生了改变,在穹顶处形成气体漩涡,最终形成环流继续前进并绕过外罐,即绕射效应。

在爆炸荷载作用下,外罐受到强烈的冲击压力。A、B、C特征点的冲击压力响应时程曲线如图9所示。

图9 爆炸荷载作用下储罐特征点处冲击压力时程曲线

从图9可知,3个特征点处超压的变化符合三角形变化规律,与图2分布形状相似。在储罐面向冲击荷载的迎爆面中心,由于迎爆面冲击波以及与罐壁接触反射回来的超压叠加,使得此处超压最大,达到0.3 MPa,即迎爆面受到的冲击影响最大。在侧爆面和背爆面的压力峰值都比较小,约为0.15 MPa。

爆炸冲击波到达3个特征点的时刻依次为8 ms、16 ms和38 ms,到达A点时绕射过程即开始,当背面B上的点超压达到最大值时,表明整个绕射过程结束,即冲击波绕过外罐用时30 ms。

分析冲击波能量耗散的过程。从A点最大0.3 MPa,到侧面C降为0.16 MPa,冲击波绕过整个罐体到背爆面B点时压力降到0.14 MPa,表明作用在结构上的压力峰值迅速下降,这与冲击波的传播规律相符。爆炸冲击波的能量耗散随着距离的增大而增多,获得的能量自然就小。按照GB6722-2014《爆破安全规程》中建筑物的破坏程度与超压的关系,当超压在0.25～0.40 MPa时,建筑物遭到中等程度破坏,钢筋混凝土顶盖出现小于1 mm的裂缝。据此也可初步判断文中采用的爆炸荷载对混凝土外罐有一定的冲击影响。

4 结语

数值仿真实验已成为工程问题物理实验教学的重要补充手段。笔者将其应用于“土木工程分析软件与应用”课程教学中,研究了基于LS-DYNA的爆炸冲击荷载在空气中传播的数值仿真实验方法,再现了爆炸冲击波的动态传播过程。通过与经验公式以及试验实测数据比对,验证了数值仿真实验方法的可靠性。将数值仿真实验方法用于大型LNG储罐的抗爆问题研究,可以进行爆炸冲击波对混凝土外罐影响的初步判断。

References)

[1] 杨文东,张艳美,俞然刚,等．复杂地质建模前处理方法在岩石力学数值实验教学中的应用[J]．实验技术与管理,2014,31(9):179-182，191．

[2] 解盘石,伍永平．多元数值仿真技术在采矿工程实验教学中的应用[J]．实验技术与管理,2013,30(3):89-91．

[3] 杨文东,张如林,黄思凝,等.数值仿真在石油院校实验教学中的应用[J]．实验室研究与探索,2016,35(1):58-60.

[4] Petersen C M. Analysis of the LPG disaster in Mexico City[J]．Journal of Hazardous Materials,1988,20(1):85-107.

[5] 胡华权,裴明敬,许学忠,等．燃料空气炸药爆炸威力评价方法研究[C]//第四届全国爆炸力学实验技术学术会议论文集．合肥:安徽省力学学会,2006:313-318.

[6] 周保顺,张立恒,王少龙．TNT炸药爆炸冲击波的数值模拟与实验研究[J]．弹箭与制导学报,2010,30(3):88-90.

[7] 张陶,惠君明,解立峰,等．FAE爆炸场超压与威力的实验研究[J]．爆炸与冲击,2004,24(2):176-181.

[8] 董桂旭,杜茂华,黄雪峰．某型炸药的冲击波超压峰值计算公式参数的修正[J]．海军航空工程学院学报,2010,25(5):542-544．

[9] 郭炜,俞统昌,金朋刚．三波点的测量与实验技术研究[J]．火炸药学报,2007,30(4):55-57．

[10] 王建灵,郭炜,冯晓军．TNT、PBX和Hexel空中爆炸冲击波参数的实验研究[J]．火炸药学报,2008,31(6):42-44.

[11] 杨鑫,石少卿,程鹏飞．空气中TNT爆炸冲击波超压峰值的预测及数值模拟[J]．爆破,2008,25(1):15-19.

[12] Wu Chengqing,Hao Hong．Modeling of simultaneous ground shock and from surface Explosions[J]．International Journal of Impact Engineering,2005,31(6):699-717.

[13] 国家质量监督检验检疫总局．GB6722—2014爆破安全规程[S]．北京:中国标准出版社,2014．

[14] 段会忠．LNG接收站储罐区泄漏扩散与火灾爆炸危险探析[J]．武警学院学报,2012,28(4):36-38.

Application of numerical simulation experiment method of explosive shock wave in the air

Zhang Rulin1, Cheng Xudong1, Zhang Yanmei1, Jia Juanjuan1,2

(1. College of Pipeline and Civil Engineering, China University of Petroleum, Qingdao 266580, China； 2. China Mobile Communications Group Shandong Co., Ltd, Qingdao Branch, Qingdao 266000, China)

A numerical experiment method is studied for explosive hock wave propagation in the air, and the peak overpressure calculated by various empirical formulas is compared and the difference reasons are analyzed. By using three modeling methods including LS-DYNA software, ALE algorithm and fluid-solid coupling theory, a numerical simulation technology is proposed for blast shock wave. The peak overpressure results obtained by numerical experiment are compared with blasting test measured data and the empirical formula results, which verifies the effectiveness of numerical simulation experiment. Finally, the explosion shock response of LNG storage tank was analyzed, and the diffraction process is obtained after the shock wave encountered the tank structure. The overpressure response is obtained at characteristics positions, which also shows that the proposed numerical experiment method can be used in antiknock performance studies for LNG storage tank.

explosive shock wave; numerical simulation experiment; ALE algorithm; LNG storage tank

10.16791/j.cnki.sjg.2017.02.029

2016-08-08 修改日期：2016-12-10

国家自然科学基金项目(51408609)；山东省高等学校科技计划项目(J14LG51)；中国石油大学(华东)青年教师教学改革项目(QN201418)；山东省研究生教育创新计划项目(SDYY15140)；中国石油大学(华东)校级研究生教学改革重点项目(YJA1408)

张如林(1983—),男,山东冠县,博士,讲师,从事土木工程数值仿真实验方面的教学与研究.

O382；TJ55

A

1002-4956(2017)2-0110-06