考虑非线性摩擦模型的机器人动力学参数辨识

席万强 陈 柏 丁 力 吴洪涛 谢本华

(南京航空航天大学机电学院， 南京 210016)

考虑非线性摩擦模型的机器人动力学参数辨识

席万强 陈 柏 丁 力 吴洪涛 谢本华

(南京航空航天大学机电学院， 南京 210016)

针对机器人动力学参数辨识的问题，提出了一种基于人工蜂群算法的辨识方法。考虑到关节摩擦特性，引入非线性摩擦模型，推导了机器人动力学模型的非线性形式。设计满足速度、加速度边界条件的五阶傅里叶级数作为激励轨迹来采集实验数据；利用人工蜂群算法，以蜂群为搜索单位，通过群体间的信息交流方式与优胜劣汰机制，对模型中的未知参数进行了辨识。最后，对得到的辨识模型进行了分析与验证，结果表明通过辨识得到关节预测力矩与测量力矩有较高的匹配度，所建立的非线性模型能够更好地描述机器人的动力学特性。

机器人; 参数辨识; 非线性摩擦模型; 人工蜂群算法

引言

工业机器人是一种集机械、控制、计算机、人工智能等跨学科先进技术于一体的高端制造业中重要的智能装备，近年来一直是国内外研究的热点[1-3]。在重载、高速工况下，实现机器人高精度的轨迹跟踪需要设计基于动力学模型的控制器。然而，由于机器人是一个多变量、强耦合的非线性系统[4]，获得其适用的数学模型难度很大。为了建立精确的机器人动力学模型，需要对其进行参数辨识研究。

机器人的参数辨识一般分为5个步骤：动力学建模、激励轨迹设计、数据采集及预处理、参数估计和模型验证。通常，机器人动力学模型中包含有摩擦模型，而摩擦模型在关节换向处影响很大[5]。PFEIFFER等[6]提出了一种由粘滞摩擦和库伦摩擦组成的线性摩擦模型，但这种简单模型并不能描述机器人在低速时的摩擦特性；GROTJAHN等[7]通过分析关节摩擦特性，采用线性的经验项来补偿上述模型，并取得了很好的辨识效果；吴文祥等[8]采用非线性形式的Stribeck模型来描述关节摩擦，并用连续的线性函数来逼近Stribeck模型，但仍未解决由于关节换向导致摩擦补偿力矩发生突变的问题；KERMANI等[9]将LuGre摩擦模型引入到机器人动力学模型中，在二自由度和四自由度机器人参数辨识中取得了不错的结果。

本文将一种非线性摩擦模型加入到六自由度串联型机器人动力学模型中。然后，设计满足速度、加速度边界条件的五阶傅里叶级数作为激励轨迹，并使用平均化滤波法和五点三次平滑法对采样数据进行预处理。在参数估计中，根据人工蜂群算法(Artificial bee colony algorithm，ABC算法)优越的寻优性能，即通过雇佣蜂搜索、跟随蜂搜索和侦察蜂搜索来获得模型中待辨识参数的最优值。最后，根据实验结果对非线性动力学模型的准确性和辨识算法的有效性进行验证。

1 非线性动力学模型

对于n自由度串联型机器人，其刚体动力学方程可由Newton-Euler法或Lagrangian法[10]获得

(1)

机器人关节换向，即在速度为零处，控制器的输出极易因测量噪声与数据量化误差产生高频跳变，并激发高频信号。这导致经典的粘滞-库伦摩擦模型不能完全描述关节摩擦特性。本文采用DAEMI和HEIMANN提出的非线性摩擦模型[7]对关节摩擦建模，则关节i(i=1,2,…,n)处的摩擦力矩为

(2)

根据文献[11]，机器人动力学模型(除摩擦模型外)可改写成关于惯性参数的线性形式

(3)

式中τs∈Rn——电机力矩向量Φs∈Rn×10n——辨识矩阵或观测矩阵θs∈R10n——惯性参数向量

其中，连杆i的惯性参数向量可表述为

(4)

式中Ixxi、Ixyi、Ixzi、Iyyi、Iyzi、Izzi——连杆i相对于坐标系i原点的各惯性张量的6个分量

rxi、ryi、rzi——质心位置

mi——连杆i的质量

另外，Φs不是满秩矩阵，因为并不是每个惯性参数都对关节力矩有影响，故需通过线性重组的方式去除冗余的惯性参数[12]，从而得到一组最小惯性参数集。式(3)可改写成

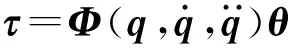
(5)

式中Φ∈Rn×p——观测矩阵θ∈Rp——包含连杆最小惯性参数集的向量p——最小惯性参数集的个数

因此，机器人非线性动力学模型可表示为

(6)

式中τf∈R4n——摩擦力矩向量 4n——摩擦参数的个数

可以看出，利用最小二乘法不能对方程(6)进行求解，故本文采用ABC算法来寻找其最优解。

2 ABC辨识算法

ABC算法[13]是对蜜蜂群体觅食行为的模拟，它主要由3部分组成：雇佣蜂、待工蜂和蜜源。其中，待工蜂又可分为跟随蜂和侦察蜂[14]。对于机器人的参数辨识问题，ABC算法将其每个待辨识的未知参数看作为一个蜜源，根据雇佣蜂搜索、跟随蜂搜索和侦察蜂搜索的机制，通过采集控制输入的激励轨迹和控制输出的关节力矩、关节位置等信息作为训练样本，进行寻优计算获得最优参数。算法的具体步骤如下：

(1)种群初始化。算法随机产生N组解，即蜜源。蜜源xij(i=1,2,…,N;j=1,2,…,D)由

(7)

随机产生数值，对实验结论没有影响。

(2)收益度计算。收益度fiti为

(8)

其中

根据fiti的大小保留蜜源质量较高的前N/2组解。需指出，fiti越大，模型辨识的精度也就越高。

(3)雇佣蜂搜索。在第T代时，雇佣蜂对已开采N/2组蜜源的邻域内进行局部搜索，并产生新的蜜源。为保证算法向最优方向进化，利用贪婪算子来择优保留优良蜜源。具体的数学描述为

(9)

其中r∈[1,2,…,N/2]且r≠i

(10)

(4)跟随蜂搜索。跟随蜂概率为

(11)

根据式(11)选择雇佣蜂进行跟随搜索，而雇佣蜂找到的蜜源质量越高，被选择跟随的概率也就越大。另外，跟随蜂搜索也通过贪婪算子来择优保留搜寻结果。

(5)侦察蜂搜索。对于当前被开采的一组蜜源xij，当搜索次数trial超过某个阈值Limit时，若算法尚未更新已找到的最优解，则当前蜜源被放弃，相应的雇佣蜂也变成侦察蜂并根据式(9)重新进行搜索。

(6)输出当前最优解，然后返回至雇佣蜂搜索，使得算法进化到下一代并反复循环迭代，直到终止条件T=Tmax。

ABC辨识算法的流程图如图1所示。

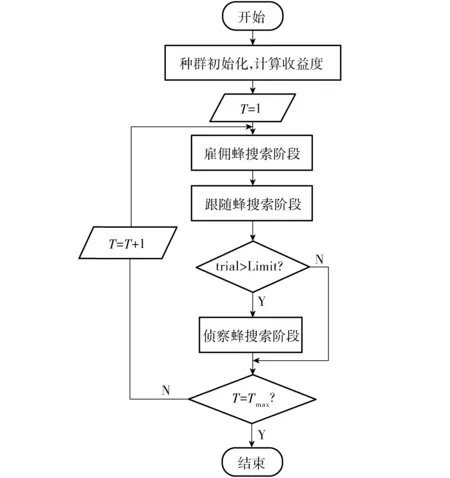
图1 ABC辨识算法的流程图Fig.1 Procedure of ABC identified algorithm

3 激励轨迹设计

(12)

式中t——激励时间ωf——基频qi,0——关节位置的补偿量K——谐波项个数ai,η、bi,η——正弦项、余弦项的幅值

每个傅里叶级数含有2K+1个参数。

为了减小动力学参数对测量误差的敏感，需对激励轨迹进行优化。由于激励轨迹受到关节位置、电机力矩、关节加速度、工作空间等条件约束，因此激励轨迹的优化问题可描述为

(13)

4 采样数据预处理

机器人通过PID控制器连续重复跟踪激励轨迹，同时对电动机电流和关节位置信号进行采样，而电动机电流通过转矩常数转换为电动机力矩信号。需要指出是，样本数据是在机器人起动时刻瞬态效应消失后进行采样的。由于采样得到的数据会受到噪声污染，若直接将该数据用于参数辨识，会降低辨识的精度，因而需对采样数据进行预处理。

由于通过激励轨迹所采集的数据具有周期性，故对原始数据进行时域平均化滤波法来提高信噪比，即

(14)

式中qs(k)、xs(k)——第s个周期内第k次采样得到的关节位置与电动机电流数据

S——采样周期次数

为了使采集数据平滑，采用五点三次平滑法对采集数据进行平滑处理，即

(15)

这里需指出，对于数据序列反复使用式(15)可得到更加平滑的曲线，但过多的平滑也会导致原始数据信息的丢失，且越往后平滑，改善的效果也不大。另外，平滑后的数据与原始数据的误差不能超过10%。

通常，因缺少速度与加速度传感器，相应的关节速度与加速度无法直接测量，而对关节位置直接微分会放大测量中的噪声，故采用文献[16]中的解析法来估算角速度与角加速度，具体步骤为：

(1)将预处理后的关节位置数据通过最小二乘法拟合成有限傅里叶级数，即

(16)

(2)对拟合得到的傅里叶级数进行微分，得到关节角速度与角加速度，为

(17)

(18)

每个傅里叶级数含有2Ni+1个参数。

5 实验结果与分析

5.1 辨识实验

本实验采用离线辨识法，相较于在线辨识更易于实施，不需要初值且没有计算时间约束。所用的六自由度串联型机器人ER-16如图2所示。图3是对应的连杆坐标系，表1给出了ER-16的D-H参数。机器人前3个关节的动力学参数远大于后3个关节[17]，故辨识实验仅在前3关节进行。激励轨迹是基频为0.04 Hz(周期为25 s)，带宽为0.25 Hz的五阶傅里叶级数，如图4所示。机器人连续重复跟踪50个周期的激励轨迹，整个实验的采样频率为1 kHz，在1个周期内每隔10个采样点记录1组关节位置与电动机电流，共采集2 500组原始数据。机器人各关节的运动约束如表2所示。

图2 ER-16六自由度机器人Fig.2 ER-16 6-DOF robot

图3 ER-16连杆坐标系Fig.3 ER-16 links coordinate system

为了验证本文所建模型的精确性，将已提出的基于ABC算法辨识的线性模型(摩擦模型为库伦-粘滞摩擦)[18]进行对比分析。同样地，在Matlab 2012b软件环境下，设置ABC算法的初始条件为：N=30，Limit=15，Tmax=50。利用ABC算法对机器人动力学参数进行辨识，并记录下迭代过程中每代的最优收益度，迭代曲线如图5所示。从图中可以看出，ABC算法在13代时便开始收敛，收敛速度快，且最大收益度为0.781 8。

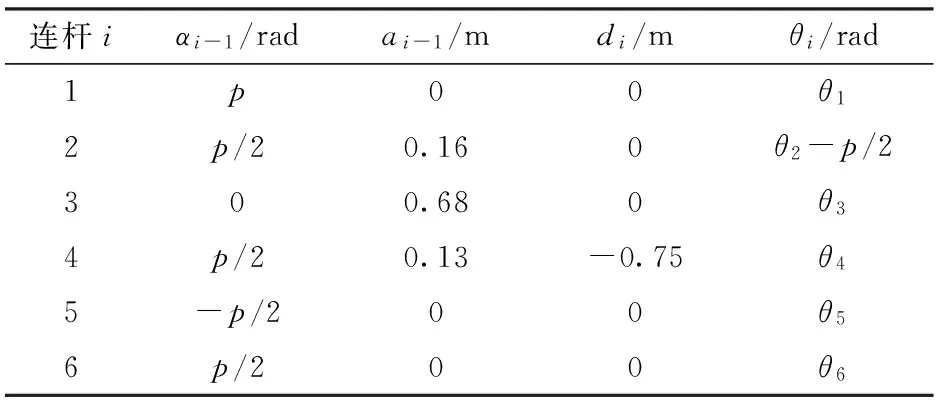
表1 ER-16连杆参数Tab.1 ER-16 parameters of links

图4 关节空间优化的机理轨迹Fig.4 Optimized exciting trajectories in joint space

参数关节最小值最大值1-180180q/(°)2-60603-170801-145145q·/((°)·s-1)2-1051053-1701701-5050q··/((°)·s-2)2-40403-65651-1200τ/(N·m)2-10003-600

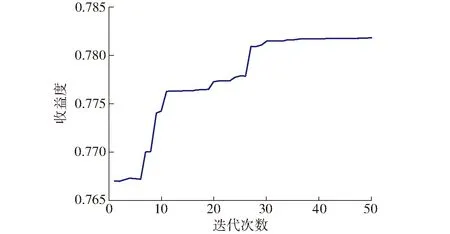
图5 ABC算法的迭代曲线Fig.5 Iterative curve of ABC algorithm

根据文献[19]可得到机器人前3关节共含有27个基本动力学参数，即15个最小惯性参数和12个摩擦参数。经ABC算法辨识的结果如表3所示。

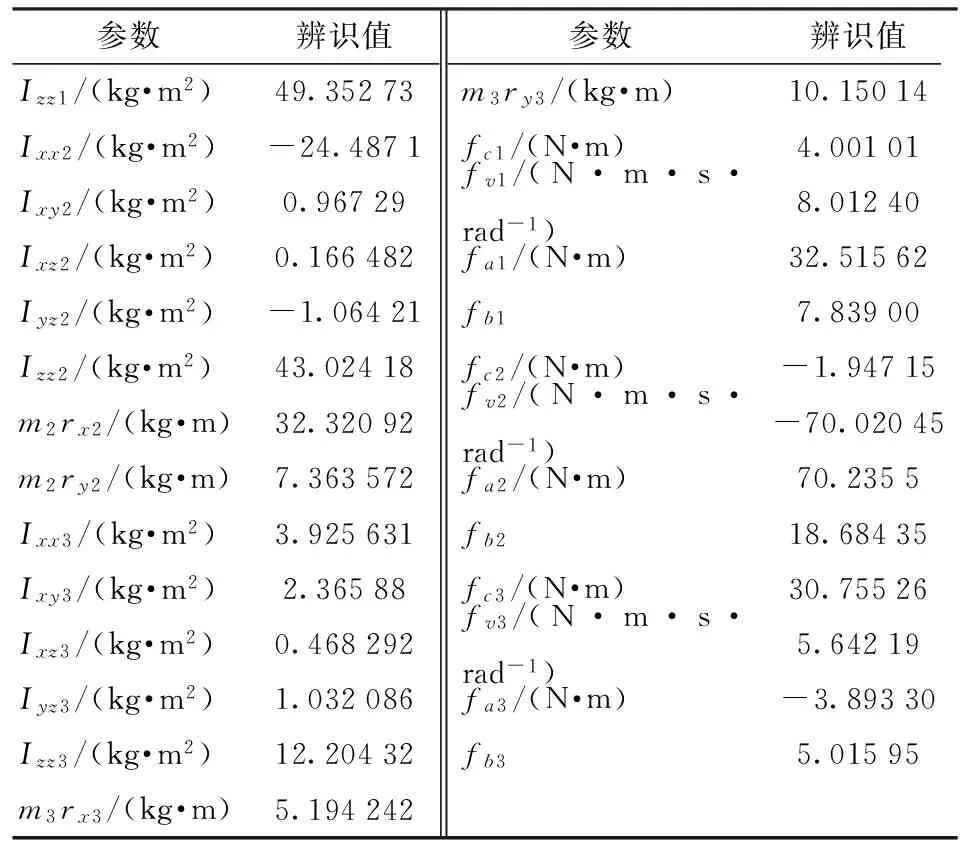
表3 机器人的动力学参数Tab.3 Dynamic parameters of robot

根据表3辨识的动力学参数与期望的运动数据可以计算出各关节力矩的预测值，同时也给出了经过线性模型得到的各关节预测力矩，对比关节力矩的预测力矩与实际测量力矩，结果如图6所示。从图中可以看出，通过2种动力学模型得到的各关节预测力矩均对测量力矩有较好的跟随性；基于非线性模型得到的预测力矩相对平滑，更适合控制器的设计。这表明，本文所建立的非线性模型准确性高，更能体现机器人关节处的摩擦特性。

5.2 模型验证

对于模型结构或模型解析式已知的系统，模型验证的任务就是确定模型中参数估计的精度[20]。参数估计的精度可以用预测输出力矩τi与实际测量力矩τpi的匹配度来衡量，匹配度计算公式为

(19)

图6 关节预测力矩与实际力矩对比Fig.6 Comparison between predicted torque and actual torque

若δ越接近100%，则说明辨识精度越高；反之，若δ越接近0，则说明辨识精度越差。前3个关节的匹配度分别为86.35%、89.96%和89.24%。匹配度高，仅在速度反转时出现误差峰值。这可能与摩擦模型在低速时无法复现复杂的动态摩擦行为有关，因而采用精确的动态摩擦模型可以有效提高辨识匹配度。说明通过ABC算法辨识机器人非线性动力学模型是有效的，能够准确反映系统的动力学特性。

为了进一步阐述辨识的精确性，图7给出了通过2种模型辨识的误差曲线。从图7a与图7b可以看出，基于非线性模型辨识的结果在关节换向处(误差峰值处)的辨识误差明显小于基于线性模型辨识得到的结果。然而，图7c中关节力矩误差减小得并不明显，其原因可能为关节3受到关节4、5、6的耦合影响，导致关节3的摩擦特性发生了改变。

图7 关节预测力矩与实际力矩的误差Fig.7 Error between predicted torque and actual torque

6 结论

(1)本文提出的辨识算法能够准确地辨识出动力学参数，算法收敛速度快、寻优能力强，能够实现对机器人驱动力矩的精确预测。

(2)与线性动力学模型相比，本文建立的非线性动力学模型有效改善了在关节换向处摩擦力矩发生突变的情况。

1 田海波, 马宏伟, 魏娟. 串联机器人机械臂工作空间与结构参数研究[J/OL].农业机械学报, 2013,44(4): 196-201. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130434&flag=1. DOI：10.6041/j.issn.1000-1298.2013.04.034. TIAN Haibo, MA Hongwei, WEI Juan. Workspace and structural parameters analysis for manipulator of serial robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(4): 196-201.(in Chinese)

2 申浩宇, 吴洪涛, 陈柏, 等. 冗余度双臂机器人协调避障算法[J/OL]. 农业机械学报, 2015,46(9): 356-361. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150952&flag=1. DOI：10.6041/j.issn.1000-1298.2015.09.052. SHEN H Y, WU H T, CHEN B, et al. Obstacle avoidance algorithm for coordinated motion of redundant dual-arm robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(9): 356-361.(in Chinese)

3 RANJBR B, MAHMOODI J, KARBASI H, et al. Robot manipulator path planning based on intelligent multi-resolution potential field[J]. International Journal of u- and e-Service, Science and Technology, 2015,8(1): 11-26.

4 孙小勇, 郑彬, 鲍捷, 等. 高速6-PSS并联机器人参数优化设计[J/OL]. 农业机械学报, 2015,46(5): 372-378.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150552&flag=1. DOI：10.6041/j.issn.1000-1298.2015.05.052. SUN X Y, ZHENG B, BAO J, et al. Parameter optimization design of high-speed 6-PSS parallel robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 372-378.(in Chinese)

5 DE WIT C C, NOEL P, AUBIN A, et al. Adaptive friction compensation in robot manipulators: low velocities[J]. The International Journal of Robotics Research, 1991,10(3): 189-199.

6 PFEIFFER F, HOLZL J. Parameter identification for industrial robots[C]∥1995 IEEE International Conference on Robotics and Automation, 1995,2: 1468-1476.

7 GROTJAHN M, DAEMI M, HEIMANN B. Friction and rigid body identification of robot dynamics[J]. International Journal of Solids and Structures, 2001,38(10): 1889-1902.

8 吴文祥, 朱世强, 靳兴来. 基于改进傅里叶级数的机器人动力学参数辨识[J].浙江大学学报: 工学版, 2013,47(2): 231-237. WU Wenxiang, ZHU Shiqiang, JIN Xinglai. Dynamic identification for robot manipulators based on modified fourier series[J]. Journanal of Zhejiang University: Enginerring Science, 2013,47(2): 231-237.(in Chinese)

9 KERMANI M R, PATEL R V, MOALLEM M. Friction identification and compensation in robotic manipulators[J]. IEEE Transactions on Instrumentation and Measurement, 2007,56(6): 2346-2353.

10 CALANCA A, CAPISANI L M, FERRARA A, et al. MIMO closed loop identification of an industrial robot[J]. IEEE Transactions on Control Systems Technology, 2011,19(5): 1214-1224.

11 QIN Z K, BARON L, BIRGLEN L. A new approach to the dynamic parameter identification of robotic manipulators[J]. Robotica, 2010,28(4): 539-547.

12 KINSHEEL A, TAHA Z, DEBOUCHAL A, et al. Robust least square estimation of the CRS A465 robot arm’s dynamic model parameters[J]. Journal of Mechanical Engineering Research, 2012,4(3): 89-99.

13 丁力, 吴洪涛, 姚裕, 等. 基于PEM-ABC算法的小型无人直升机系统辨识[J/OL]. 农业机械学报, 2016,47(1): 8-14.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160102&flag=1. DOI：10.6041/j.issn.1000-1298.2016.01.002. DING L, WU H T, YAO Y, et al. Hybrid PEM-ABC algorithm for system identification of small-scale unmanned helicopter[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(1): 8-14.(in Chinese)

14 DUAN H B, SHAO S, SU B W, et al. New development thoughts on the bio-inspired intelligence based control for unmanned combat aerial vehicle[J]. Science China Technological Sciences, 2010,53(8): 2025-2031.

15 SWEVERS J, GANSEMAN C, TUKEL D B, et al. Optimal robot excitation and identification[J]. IEEE Transactions on Robotics and Automation, 1997,13(5): 730-740.

16 SWEVERS J, GANSEMAN C, SCHUTTER J De, et al. Experimental robot identification using optimised periodic trajectories[J]. Mechanical Systems and Signal Processing, 1996,10(5): 561-577.

17 SWEVERS J, VERDONCK W, SCHUTTER J De. Dynamic model identification for industrial robots[J]. IEEE Control Systems, 2007,27(5): 58-71.

18 DING L, WU H, YAO Y, et al. Dynamic model identification for 6-DOF industrial robots[J]. Journal of Robotics,2015.

19 霍伟．机器人动力学与控制[M]．北京: 高等教育出版社, 2005.

20 DING F, LIU X P, LIU G. Identification methods for Hammerstein nonlinear systems[J]. Digital Signal Processing, 2011,21(2): 215-238.

Dynamic Parameter Identification for Robot Manipulators with Nonlinear Friction Model

XI Wanqiang CHEN Bai DING Li WU Hongtao XIE Benhua

(CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

Aiming at the dynamical parameter identification for robot manipulator, the artificial bee colony algorithm for identification was proposed. Considering the friction characteristics that the friction model was unable to reappear the behavior of complex dynamic friction at low speeds, the nonlinear robot model contained the nonlinear friction model was deduced by introducing the nonlinear Daemi-Heimann model. Then, the five order Fourier series was designed as exciting trajectory to collect experimental data, which satisfied velocity and acceleration boundary conditions. With the artificial bee colony algorithm, the colony bee was employed as search unit to identify unknown parameters which included 15 minimum inertia parameters and 12 friction parameters in the model through exchanging the information and retaining the superior individual. Finally, the established model was validated and analyzed, and all the results demonstrated that the proposed identification algorithm can accurately identify the dynamical parameters, and it also had high-speed convergence, strong search capability and can achieve the accurate prediction of robot driving torque. Compared with the linear dynamic model, the established nonlinear dynamical model can effectively improve the condition of sudden change about friction torque at the moment of joints commutation and can well reflect the dynamical characteristics of robot.

robot; parameter identification; nonlinear friction model; artificial bee colony algorithm

10.6041/j.issn.1000-1298.2017.02.053

2016-06-14

2016-07-30

国家自然科学基金项目(51575256、51375230)

席万强(1989—)，男，博士生，主要从事工业机器人参数辨识研究，E-mail： xi_wanqiang@163.com

陈柏(1978—)，男，教授，博士生导师，主要从事介入医疗机器人和工业机器人研究，E-mail： chenbye@126.com

TP242

A

1000-1298(2017)02-0393-07