一种基于解空间分割的并行遗传算法

冯 勇 郭 军 徐红艳 付潇莹

(辽宁大学信息学院 沈阳 110036)

一种基于解空间分割的并行遗传算法

冯 勇 郭 军 徐红艳 付潇莹

(辽宁大学信息学院 沈阳 110036)

遗传算法是一种常用于NP问题中寻求近似最优解的优化方法,已被广泛应用于国防、科研、经济管理、工程建设等重要领域,但其求解过程中常出现过早收敛于局部最优解、计算复杂度高等问题。针对这些问题,论文首先给出一种基于解空间分割的并行处理机制,通过对问题解空间的分割实现求解最优化问题的并行化处理;然后将该机制引入到遗传算法中,提出了一种基于解空间分割的并行遗传算法;最后,经实验对比表明论文所提算法在并行化处理方面具有良好的线性加速比,同时证明在克服过早收敛于局部最优解方面要优于标准遗传算法和粗粒度并行遗传算法。

解空间分割; 并行化; 遗传算法; 线性加速比; 优化

Class Number TP183

1 引言

遗传算法作为一种经典的求解复杂问题最优解的算法,在电网规划、生产调度、复杂网络分析等领域得到广泛应用[1～3]。由于标准遗传算法[4]是串行算法,存在运行时间长、易陷入局部最优解的弊端,为更好满足当今大规模计算的应用需求,往往需要对标准遗传算法进行并行化改进。其中,粗粒度并行遗传算法[5]是应用最为广泛的一种并行遗传算法,具备线性加速比[6],在全局搜索上优于标准遗传算法,有抑制早熟收敛的效能[7]。为进一步提升粗粒度并行遗传算法的性能,众多学者对其进行改进,具有代表性的成果有:胡玉兰等提出子种群规模动态可变,子种群间按照其竞争能力进行迁移[8];龚雪晶等提出进化过程中动态调整各遗传参数和遗传算子,并针对自适应调整过程中带来的负载失衡加入了相应的迁移策略[9];严晓明提出对迁移算子进行改进,用公共池的方式来代替各子种群间个体迁移时的拓扑结构[10]。这些改进在不同程度上提升了算法的性能,但以牺牲算法复杂度为代价,需要预设子种群数、种群间个体迁移的拓扑顺序、个体迁移数及个体迁移时机等参数。这些参数中子种群数的划分直接影响粗粒度并行遗传算法求解效率,而由于该参数的设置与求解问题有关,故该参数难以直接设定[7]。并且,这些改进算法在克服过早收敛于局部最优解方面仍需要进一步的提升。

针对以上问题,本文首先给出了基于解空间分割的并行处理机制,然后将该机制引入到标准遗传算法中,形成了一种基于解空间分割的并行遗传算法。基于解空间分割的并行处理机制分为三阶段:第一阶段是对优化问题的解空间进行分割;第二阶段是在不同的子空间上分别对目标函数进行求解;第三阶段是对不同子空间的解汇总选出最优解作为全局解。该机制设计简单、便于实现,没有过多的预设值,对于最优化问题的求解具有很好的普适性。采用基于解空间分割机制的并行遗传算法在初始化时对运算参数进行预设定,然后对问题解空间进行分割。分割后子任务在其解空间内进行最优化求解。最后,将各子任务得出的解汇总,从中选出全局最优解。经实验对比分析,本文所给算法模型简单,没有过多的参数设定,在并行化处理上具有良好的线性加速比,在克服过早收敛于局部最优解方面优于标准遗传算法和粗粒度并行遗传算法。

2 基于解空间分割的并行处理机制

本文提出的基于解空间分割的并行处理机制是将分而治之的思想引入到对优化问题的求解中。该机制将处理过程分为分割、运算、汇总三个阶段,具体描述如下:

1) 分割阶段。对解空间进行划分,设待优化的问题共有m个自变量,即X1,X2,…,Xm,整体解空间S为m个自变量构成的m维空间,解空间的维度为自变量数。将整体解空间S进行等分分割成n份不同子空间{S1,S2,…,Sn}。

2) 运算阶段。将分割后的子空间{S1,S2,…,Sn}分别作为各子任务{K1,K2,…,Kn}的解空间,划分后的子空间数即为子任务数,子任务为最小的计算单元,各子任务{K1,K2,…,Kn}分别在其所在的解空间{S1,S2,…,Sn}中对目标函数F(X1,X2,…,Xm)进行寻优运算,得出各子任务{K1,K2,…,Kn}的最优解,对应的最优目标函数值为{A1,A2,…,An}。各子任务的寻优过程是完全独立的,子任务在各自的解空间中对优化问题求解。

3) 汇总阶段。从各子任务的解中选择最优解,将所有子任务{K1,K2,…,Kn}运算得出的函数值{A1,A2,…,An}进行汇总,从运算结果{A1,A2,…,An}中选出最优目标函数值Ax作为整体的最优目标函数值,Ax所对应的解(x1,x2,…,xm)为整体解空间中的最优解。

基于解空间分割的并行处理机制的工作流程如图1所示。

图1 基于解空间分割的并行处理机制的工作流程

3 基于解空间分割的并行遗传算法

3.1 算法理论分析

根据文献[11～12]可知选择算子采用精英选择法,即每一代选择的时候最优个体淘汰掉最差个体的遗传算法收敛到全局最优点。优化问题中函数的解空间S是所有解的集合,将其分割成n份不同子空间{S1,S2,…,Sn},即S为各子空间的并集,目标函数值是解空间中的解关于目标函数的映射,由集合论可知各子集的最优解的集合中的最优解必为整体解空间的最优解。

文献[13]提出了模式理论,文献[14]在模式理论的基础上定义了区间分割,综上可得采用解空间分割的并行处理机制的带有精英选择的遗传算法必然收敛到全局最优解。对标准遗传算法进行性能分析可知在固定迭代次数下其运算的时间复杂度为关于个体数N的O(N)。对解空间进行K等分分割,若每个子空间的个体数为N/K,可知各子群的运算时间均为原运算时间的1/K,从而达到线性加速。

3.2 算法思想

基于解空间分割的并行遗传算法相较于标准遗传算法,增加了子空间划分个数和各子空间个体数两个参数,在算法运行之前需要对这两个参数进行设定。首先,按照要求的精度选择总体样本个数,再按照子空间占总体空间的比例为每个子群分配个体。一般来说,种群划分数越多整体并行性越好,对克服过早收敛于局部最优解的效果也越好,但是随着划分数的急剧增加会使子群的个体数急剧下降从而不利于对子空间的求解,而增加子群个体数又势必降低算法的并行性,所以在实际运算中划分后的子群个体数可以在按比例划分的基础上做适当的增加并适当的增加迭代次数。另外,为保证每个子群独立寻优的可行性要求每个子群的个体数不能过少,根据Reeves[15]提出的最小规模理论在此规定各子群内的个体数不少于20。

3.3 算法描述

采用基于解空间分割的并行处理机制对遗传算法进行改进后,算法的具体运行步骤如下:

Step1 在基本遗传算法的基础上对初始参数进行设定。

Step2 分割阶段,将整体解空间S等分为n份,子种群个体数为整体个体数的n等分,如式(1)所示:

Cut:S→{S1,S2,…,Sn}

(1)

Step3 运算阶段,子任务随机产生初始种群(二进制),各子任务按遗传算法工作流程在各自的解空间上独立运行。如式(2)所示:

Compute:K1:A1=maxF(X1,X2,…,Xm)X1,X2,…,Xm∈S1

K2:A2=maxF(X1,X2,…,Xm)X1,X2,…,Xm∈S2

…

Kn:An=maxF(X1,X2,…,Xm)X1,X2,…,Xm∈Sn

(2)

Step4 汇总阶段,将各子种群运行结束后的求解结果汇总,从中选出最优值,其对应的解即为全局最优解,如式(3)所示:

Join:choose(A1,A2,…,An)→AxAx∈{A1,A2,…,An}Ax=F(x1,x2,…,xm) (x1,x2,…,xm)∈Sx

(3)

3.4 算法示例

为更好地说明算法的运行,这里给出具体示例。如果一个遗传算法的目标函数的搜索域是在二维空间中,即目标函数的自变量为X、Y,目标函数F(X,Y)=X2+Y2为关于X、Y的复杂函数。本例设种群个体数M为200、进化代数T为300、交叉概率Pc为0.6、变异概率Pm为0.01。对整体解空间即X、Y的范围进行4等份分割,每个子空间中的个体数为50。假设解空间为0≤X≤10,0≤Y≤10,将X、Y的范围空间进行4等份分割后,即分割后的4个子任务{K1,K2,K3,K4}的搜索空间{S1,S2,S3,S4}如式(4)所示:

S1∈{0≤X≤5,0≤Y≤5}

S2∈{0≤X≤5,5≤Y≤10}

S3∈{5≤X≤10,0≤Y≤5}

S4∈{0≤X≤10,5≤Y≤10}

(4)

各子空间由不同的子群并行进行搜索,每个子群采用基本遗传算法独立运算。各子任务的最优目标函数值{A1,A2,A3,A4}分别为50、125、125、200,从中选出最优目标函数值,即A4作为全局的最优目标函数值,其所对应的解X4=10、Y4=10作为全局最优解。

4 实验分析

4.1 实验环境

本文所提改进算法取Schaffer测试函数为目标函数,其函数表达如式(5)所示:

-5≤x1,x2≤5

max(F)=1

(5)

图2为Schaffer测试函数的三维立体图,从中可看出该函数有无穷个局部极大点,其中只有一个点为全局最大点,最大值为1。

图2 Schaffer测试函数的三维立体图

本文中所用的实验预设参数为:种群个体M为200、进化代数T为300、交叉概率Pc为0.6、变异概率Pm为0.01,选择策略采用精英法,交叉为单点交叉,实验的结果为1000次重复实验的平均值,精度为0.0001。粗粒度并行遗传算法子种群个数分别取4、9、16、25,迁移操作采用环状拓扑,迁移规模为4的最佳→最差准则,迁移间隔为5的定周期迁移策略。基于解空间的并行遗传算法分别将解空间分割为4、9、16、25等分。实验环境为局域网中25台装有Ubuntu14.04 64位操作系统,CPU为Intel I5 4250型号的计算机作为计算节点组成的分布式计算集群。编程语言为Python2.7。

4.2 实验结果

在上述实验环境下,对Schaffer函数进行最优化求解,实验结果如下:

1) 标准遗传算法、粗粒度并行遗传算法的运行用时如表1所示。

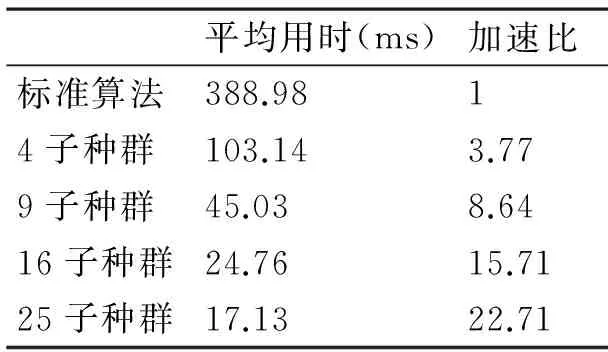
表1 标准遗传算法与粗粒度并行遗传算法的运行用时

2) 标准遗传算法、基于解空间分割的并行遗传算法的运行用时如表2所示。

表2 标准遗传算法与基于解空间分割的并行遗传算法的运行用时

经计算后,得到的解情况如下:

1) 标准遗传算法最终解为0.9917。

2) 粗粒度并行遗传算法的最终解如表3所示。

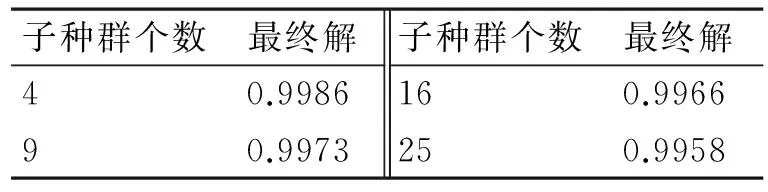
表3 粗粒度并行遗传算法的最终解

3) 基于解空间分割的并行遗传算法最终解如表4所示。

表4 基于解空间分割的并行遗传算法最终解

4.3 结果分析

在并行性能方面,与标准遗传算法对比,可以看出改进算法具有很好的并行性能,可以达到良好的线性加速比。

在计算性能方面,粗粒度的并行遗传算法在克服过早收敛于局部最优解方面优于标准遗传算法,改进算法在空间分割为4等分、9等分和25等分时最优解的求解效果优于其他算法。9等分和25等分时求解的最优解在精度上可以近似认为已到达实际最优解,16等分时效果要稍差于粗粒度遗传算法但仍然优于标准遗传算法,由此可见基于解空间分割的并行遗传算法在并行化和克服局部最优解方面相对于传统的串并行遗传算法确有提升,但不同的分割方式对求解效果有一定的影响,在具体的解空间划分方式及子群个体分配上仍需要进一步的深入研究和完善。

对实验中各算法的计算性能进行分析,粗粒度并行遗传算法采用子种群划分及种群间个体迁移,增加了全局的搜索能力,对比基本遗传算法减少了未成熟收敛的可能性。但是各子种群都是在整体解域空间中进行求解,存在重复求解的问题,同时各子种群具有更少的个体数,解空间的范围和解的精度并没有改变,这样必然导致子种群更容易陷入局部最优解。保证种群多样性的个体迁移,可能会使陷入局部最优解的子种群的个体迁移到其他子种群,使被迁移入的子种群受到污染并造成其加快早熟。子种群数不同会得到不同的求解效果,但是最好的子种群数无法直观地确定,只能经过多次实验确定。

改进算法中子种群完全独立运行,不存在个体迁移带来的污染问题,同时对潜在的最优解具有保护作用。各子种群采用的是不同的子解域空间,各子种群的个体数量为整体个体数按其子空间占整体解空间的比例划分,可以减少由于子种群个体数量的减少带来的子种群早熟可能性。解空间的划分可以很好避免导致早熟的高适应度个体对整体求解效果的影响,使最优解所在的子空间减少非全局最优解的高适应度个体的存在。

5 结语

为提升并行遗传算法的性能及克服过早收敛问题,本文提出了一种基于解空间分割的并行处理机制,并在此基础上给出了一种基于解空间分割的并行遗传算法,改进算法对问题解空间进行分割,使分割后的子任务在其解空间内进行最优化求解,将各子任务得出的解汇总,从中选出全局最优解。最后,经实验分析表明本文所提算法设计简单、便于实现、没有过多的参数设定,在并行化处理方面具有良好的线性加速比,同时在克服过早收敛于局部最优解方面要优于标准遗传算法和粗粒度并行遗传算法。

[1] 黄慧,顾波.改进遗传算法在电网规划中的应用[J].电力系统保护与控制,2012,40(22):65-67. HUANG Hui, GUO Bo. Application of improved genetic algorithm in power network planning[J]. Power System Protection and Control,2012,40(22):65-67.

[2] 张国辉,高亮,李培根,等.改进遗传算法求解柔性作业车间调度问题[J].机械工程学报,2009,45(7):146-151. ZHANG Guohui, GAO Liang, LI Peigen, et al. Improved Genetic Algorithm for the Flexible Job-shop Scheduling Problem[J]. Journal of Mechanical Engineering,2009,45(7):146-151.

[3] 金弟,刘杰,杨博,等.局部搜索与遗传算法结合的大规模复杂网络社区探测[J].自动化学报,2011,37(7):874-882. JIN Di, LIU Jie, YANG Bo, et al. Genetic Algorithm with Local Search for Community Detection in Large-scale Complex Networks[J]. Acta Automatica Sinica,2011,37(7):874-882.

[4] Goldberg D E. Genetic Algorithms in Search, Optimization and Machine Learning[M]. MA: Addison-Wesley,1989:80-86.

[5] 郭彤城,慕春棣.并行遗传算法的新进展[J].系统工程理论与实践,2002(2):16-21. GUO Tongcheng, MU Chundi. The Parallel Drifts of Genetic Algorithms[J]. System Engineering Theory and Practice,2002(2):16-21.

[6] Lienig J. A Parallel Genetic Algorithm for Performance-driven VLSI Routing[J]. IEEE Trans on EC,1997,1(1):29-39.

[7] 岳嵚,冯珊.粗粒度并行遗传算法的计算性能分析[J].武汉理工大学学报,2008,30(7):108-110. YUE Qin, FENG Shan. Performance Analysis of the Coarse-grained Parallel Genetic Algorithms[J]. Journal of WuHan University of Technology,2008,30(7):108-110.

[8] 胡玉兰,潘福成,梁英,等.基于种群规模可变的粗粒度并行遗传算法[J].小型微型计算机系统,2003,24(3):535-536. HU Yulan, PAN Fucheng, LIANG Ying, et al. Parallel Genetic Alogrithm Based on Population Size Mutable Coarse-grained[J]. Journal of Chinese Mini-Micro Computer Systems,2003,24(3):535-536.

[9] 龚雪晶,慈林林,姚康泽,等.顾及负载平衡的并行多种群自适应遗传算法[J].系统仿真学报,2009,21(17):5396-5398. GONG Xuejing, CI Linlin, YAO Kangze, et al. Parallel Multi-population Adaptive Genetic Algorithm by Considering Work Load Balance[J]. Journal of System Simulation,2009,21(17):5396-5398.

[10] 严晓明.粗粒度并行遗传算法迁移算子的一种改进[J].福建师范大学学报(自然科学版),2013,29(1):43-47. YAN Xiaoming. An Improved Migrate Operator of Coarse-Grained Parallel Genetic Algorithm[J]. Journal of Fujian Normal University(Natural Science Edition),2013,29(1):43-47.

[11] 陈国良.遗传算法及其应用[M].北京:人民邮电出版社,1996:202-214. CHEN Guoliang. Genetic algorithm and its application[M]. Beijing: Posts and Telecom Press,1996:202-214.

[12] Rudolph G. Convergence Analysis of Canonical GA[J]. IEEE Trans on Neural Networks,1994,5(1):96-101.

[13] Holland J H. Adoption in Natural and Artificial Systems[M]. Massachusetts Institute of Technology Press,1975:126-137.

[14] 刘守生,于盛林,丁勇,等.基于均匀分割的多种群并行遗传算法[J].数据采集与处理,2003,18(2):143-145. LIU Shousheng, YU Shenglin, DING Yong, et al. Multipopulation Parallel Genetic Algorithm Based on Even Partition[J]. Journal of Data Acquisition and Processing,2003,18(2):143-145.

[15] Reeves C R. Using genetic algorithms with small populations[C]//Proceedings of the 5th international conference on genetic algorithms, San Francisco: Morgan Kaufmann Publishers,1993:92-97.

A Parallel Genetic Algorithm Based on Solution Space Division

FENG Yong GUO Jun XU Hongyan FU Xiaoying

(School of Information, Liaoning University, Shenyang 110036)

Genetic algorithm is a kind of the optimization method which is commonly used in NP problem for approximate optimal solution, and it has been widely used in national defense, scientific research, economic management, engineering construction, and other important fields. But some problems often appear during its solving process, such as premature convergence to local optimal solution and the high computational complexity. To solve these problems, first of all, this paper proposes a parallel processing mechanism based on the solution space division which implement parallel processing to solve the optimization problem by dividing the problem solution space. Then the mechanism is introduced into the genetic algorithm, and this paper proposes a parallel genetic algorithm based on the solution space division. Finally, the experimental comparison indicate that the proposed algorithm in parallel processing has a good linear speedup, at the same time overcoming the premature convergence to local optimal solution is better than the standard genetic algorithm and coarse-grained parallel genetic algorithm.

solution space division, parallelization, genetic algorithm, linear speedup, optimization

2016年8月12日,

2016年9月25日

辽宁省本科教学改革项目(编号:201607);辽宁省自然科学基金项目(编号:2013020031);辽宁省档案科技项目(编号:L-2016-R-7)资助。

冯勇,男,博士,教授,研究方向:数据挖掘和个性化推荐。郭军,男,硕士研究生,研究方向:数据挖掘和个性化推荐。徐红艳,女,硕士,副教授,研究方向:数据库技术、deep web。付潇莹,女,研究方向:数据挖掘和个性化推荐。

TP183

10.3969/j.issn.1672-9722.2017.02.007