基于统计公差的全景天窗主密封条压缩量的研究

欧阳帆

Ou Yangfan

（同济大学 机械与能源工程学院，上海 200092；伟巴斯特车顶供暖系统（上海）有限公司，上海 201108）

基于统计公差的全景天窗主密封条压缩量的研究

欧阳帆

Ou Yangfan

（同济大学 机械与能源工程学院，上海 200092；伟巴斯特车顶供暖系统（上海）有限公司，上海 201108）

密封条作为天窗上一个重要功能零件，不仅起着防水、防尘和隔音降噪等密封作用，还在天窗玻璃开启关闭或天窗安装过程中与配合环境零件产生压缩、摩擦等作用，其与配合环境零件的压缩量及公差的设定非常关键。压缩量设定过小时，密封条无法发挥正常功能；压缩量设定过大，则可能造成天窗开启关闭过程中产生异响、天窗无法正常开启或天窗无法在整车上安装。

汽车天窗；密封条；压缩量；尺寸链；累计公差

0 引 言

近10年来，我国汽车市场飞速发展，每年上市销售的各类改款及全新乘用车型多达数百种，市场扩大的同时，各整车厂商之间的竞争也日趋激烈。

天窗作为增加整车舒适性的一项外饰类功能零件，逐渐成为各上市新车型的必备配置。尤其是高档的外滑式全景天窗（Outer Sliding Roof，OSR），越来越多地出现在目前火爆的 SUV车型和其他高档乘用车型上。

密封条在天窗上起到防水、防尘、防漏气、隔音和一定的美观作用，是天窗上的关键零件。密封条与周边环境件的压缩量设定至关重要，该值若设定不当，密封条不仅无法起到上述作用，甚至还会发生密封条外观起皱，天窗关闭或开启时产生异响等问题。文中主要探讨安装在天窗框架上OSR主密封条的压缩量设定，并以某款OSR上的主密封条为例，分析统计公差在该密封条与周边零件压缩量设定上的应用。

1 累计公差尺寸链的计算方法

1.1 极值公差法

极值公差法是在考虑零件尺寸最不利的情况下，通过尺寸链中尺寸的最大值或最小值来计算目标尺寸的值及公差的方法。此方法一般适合功能性零件，要求在最恶劣的情况下，零件也必须满足要求。主要有以下几点：

1）封闭环的基本尺寸等于各增环的基本尺寸之和减去各减环的基本尺寸之和。

式中，N为封闭环的基本尺寸，mm；Ai为增环的基本尺寸，mm；Aj为减环的基本尺寸，mm；m为增环的数目；n为组成环数目。

2）封闭环的上偏差等于各增环的上偏差之和减去各减环的下偏差之和。3）封闭环的下偏差等于各增环的下偏差之和减去各减环的上偏差之和。

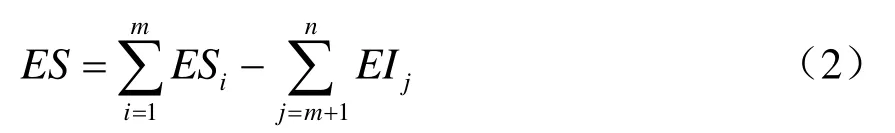
1.2 统计公差法

统计公差法是在各装配零件大批量生产且生产过程均采用统计过程控制、各零件的尺寸公差的概率分布符合正态分布且装配尺寸链较长（一般不少于 3个环）的情况下，利用各独立的正态分布的方差可叠加原理（装配部件中各零件的尺寸分布绝大部分情况下都是互相独立的）来计算目标尺寸的公差。此方法适用于大部分功能要求不高的零件，而且允许极少数的情况下，当各零件都处于最恶劣的情况时总成零件出现较低的、可以接受的不良率。主要有以下几点：

1）封闭环的基本尺寸等于各增环的基本尺寸之和减去各减环的基本尺寸之和。

式中，N为封闭环的基本尺寸，mm；Ai为增环的基本尺寸，mm；Aj为减环的基本尺寸，mm；m为增环的数目；n为组成环数目。

2）当各环的基本尺寸均为尺寸统计值的中值情况时，封闭环公差为各环公差平方和的算术平方根。

式中，T为封闭环的公差，mm；Tsi为各组成环的平均统计公差，mm；n为组成环数目。

2 影响OSR主密封条压缩量累计公差尺寸链的因素

图1 OSR

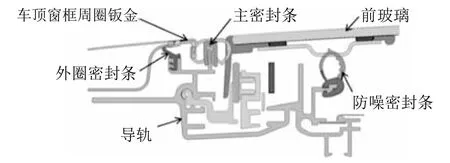
图2 断面A-A（主密封条安装于天窗窗框总成上）

2.1 密封条的安装方式

OSR（如图1所示）主密封条可安装于车顶窗框上，也可安装于天窗框架上，不同的安装方式会造成决定主密封条压缩量公差的装配尺寸链的各个环不同。主密封条装于天窗框架（导轨为天窗框架一部分）上时（如图2所示），主密封条为“双泡”结构，其外侧与车顶窗框存在压缩。主密封条安装于车顶窗框上时（如图3所示），主密封条为单泡结构，其外侧与车顶框架间用密封胶粘结固定。

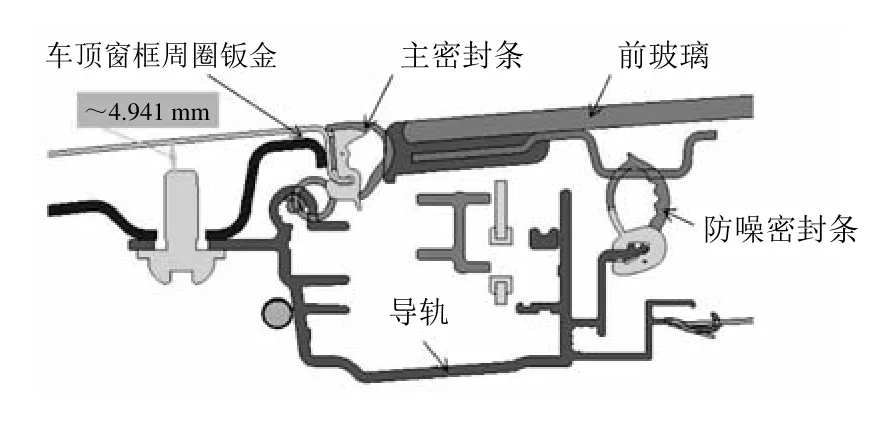
图3 断面A-A（主密封条安装于车顶窗框上）

2.2 天窗在整车上的装配方式及天窗各相关零件的装配关系

不同安装方式造成天窗相对车顶窗框的位置公差不同。OSR的前玻璃是装在运动机构的连杆上，运动机构在天窗导轨内滑动以实现天窗前玻璃的起翘和开闭。在计算主密封条与前玻璃总成的接触压缩量的公差尺寸链时，各组成环是从前玻璃总成到运动机构件，然后到导轨，再到主密封条，最后的封闭环是主密封条与前玻璃的压缩量。

3 某车型配备的OSR上主密封条压缩量公差的研究

某车型上采用的密封条（如图4所示）与图2中的断面类似，其外侧泡与车顶窗框翻边压缩，内侧泡与天窗前玻璃注塑总成包边压缩。文中所研究的是这2个压缩量结合统计公差的设定方法。

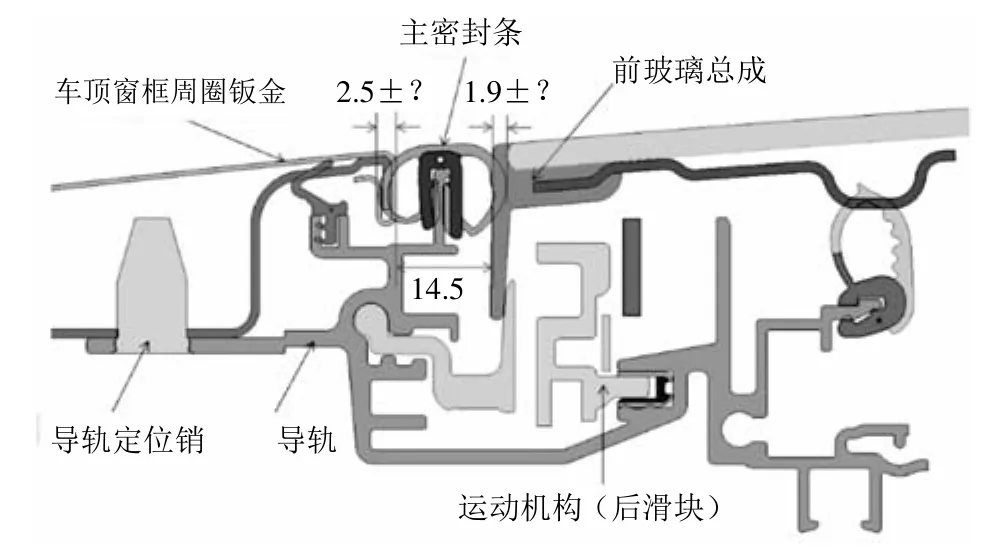
图4 断面A-A（天窗导轨位置处断面）

封闭环基本尺寸的计算，可以在应用CAD软件时，在3D模型中直接量取或事前设定，产品开发工程师通常关注如何确定封闭环的公差分布，之后才能结合产品功能确定封闭环基本尺寸（设计名义值）是否设定合理。

主密封条外侧泡与车顶窗框翻边的压缩量名义值暂定为2.5 mm，内侧泡与前玻璃总成注塑包边的压缩量名义值暂定为1.9 mm。

主密封条外侧泡与车顶窗框翻边的压缩量作为尺寸链中的封闭环，根据天窗在整车上的装配方式及天窗各相关零件的装配关系，其组成环为6个，见表1。 mm

表1 主密封条外侧泡与车顶翻边压缩量计算

采用极值公差计算，主密封条外侧泡与车顶窗框翻边的压缩量最小值为0.45 mm，可以接受；最大压缩量达到4.55 mm，在此压缩量下，密封条对车顶窗框翻边的压缩回弹力过大，且此侧密封条海绵胶与密实胶的间隙只有5.87 mm-4.55 mm =1.32 mm（如图5所示），两者结合造成天窗在整车上安装困难。采用统计公差计算，压缩量在1.41～3.59 mm（2.5±1.09 mm）间，无上述问题。

主密封条内侧泡与天窗前玻璃总成注塑包边的压缩量作为一个尺寸链中的封闭环，根据天窗各相关零件的装配关系，其组成环为13个，见表2。了解其组成环的公差分布后，可以计算出该封闭环的公差分布。根据极值法计算，其尺寸为1.9±3.5 mm；根据统计法计算，其尺寸为1.9±1.23 mm。

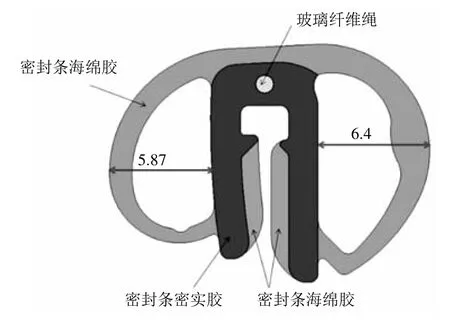
图5 密封条断面

表2 主密封条内侧泡与前玻璃总成注塑包边压缩量计算mm

采用极值公差计算，主密封条内侧泡与前玻璃总成的压缩量最小值为-1.6 mm，此侧密封条和前玻璃总成已无压缩，会产生漏气、漏光等问题，此值不可接受；最大压缩量达到5.4 mm，此时，不仅密封条回弹力很大，且此侧密封条海绵胶与密实胶间隙只有6.4 mm-5.4 mm =1 mm（如图5所示），这会造成天窗总成前玻璃开启和关闭力很大，且容易产生摩擦异响。采用统计公差计算，压缩量在0.67～3.13 mm（1.9±1.23 mm）间，无上述问题。

在用极值法计算主密封条两侧压缩量公差时要解决上述问题，只能将密封条断面上两侧的海绵胶泡加大，外侧至少加大0.5 mm，压缩量的名义值可维持2.5 mm不变。内侧海绵胶泡至少需要加大 4 mm，并将压缩量的名义值调整为4 mm，两者结合，图4中天窗在整车上主密封条可见宽度的名义值将由14.5 mm增大到16.9 mm（假定密封条原来两泡总高度为x，且由图4可知，密封条可见宽度为x -1.9-2.5=14.5 mm，则两侧泡加高后总高度为x+0.5+4=x+4.5，可得出密封条可见宽度为x+4.5-4-2.5=16.9 mm），会造成天窗总成外观质量下降并增加主密封条成本，这种做法不可取。

4 结 论

极值法求解尺寸链时，封闭环公差是由各组成环公差累加得到，各零件具有完全互换性。当封闭环公差要求较高，组成环较多时，各个组成环公差势必很小，这会对加工精度要求提高，增加制造成本。

采用统计方法计算的封闭环公差比用极值法计算出的要小，因此其允许更大的制造公差，在制造成本上更经济，可以引入安全系数来达到制造成本和风险的平衡，采用统计法时要确保特征符合规律分布和具有独立性的条件。理论尺寸和公差可输入到电子表格中进行叠加计算。

在制造过程受控且稳定的条件下，零件加工时其尺寸处于公差带范围的中间部分是多数，接近极限尺寸是极少数。多个零件在装配时，各组成环恰好都接近极限尺寸的可能性更小。因此，按统计公差方法求解零件的尺寸公差在现实生产中具有合理性，但如果零件的生产数量小，没有达到批量生产的条件，不满足零件100%互换性一般要求时，特征的尺寸公差不存在分布概率的问题，因此这种情况下只能采用极值法进行分析。

[1]蔡延波，曹增强，李志成. 复杂装配尺寸链的分析计算[J]. 现代制造工程，2008（4）：81-84.

[2]喻鹏飞. 公差叠加分析方法概述[J]. 机械研究与应用，2010（1）：61.

[3]张国莹，张琦，王云浩，等. 装配尺寸链的应用分析[J]. 摩托车技术，2011（5）：40-42.

[4]阎艳，余美琼，王国新，等. 平面尺寸链公差分析算法研究[J].北京理工大学学报，2011，31（7）：799-802.

[5]邹石英. 统计公差在装配尺寸链中的应用[J]. 现代企业教育，2011（14）：196-197.

[6]张宇. 面向质量目标的统计公差应用概述[J]. 机械工业标准化与质量，2012（10）：15-18.

[7]崔庆泉. 轿车尺寸同步工程实施综述[J]. 机械研究与应用，2013（6）：191-194.

[8]田凤荣，徐晶才，李瑞生，等. 尺寸工程在内饰件设计中的应用[C]. 沈阳科学学术年会，2013.

[9]周清华. 尺寸链分析技术及其在车身开发中的应用[C]. 中国汽车工程学会年会，2013.

[10]李广利. 在尺寸链中统计公差的目标设计[J]. 低压电器，2013（12）：12-14.

U463.85.06

：ADOI：10.14175/j.issn.1002-4581.2017.01.004

1002-4581（2017）01-0013-04

2016− 08− 16