矩形旋转交错网格PML边界条件的研究与实现

张 亮，孙尽尧

（武汉大学 物理科学与技术学院，湖北 武汉430072）

矩形旋转交错网格PML边界条件的研究与实现

张 亮，孙尽尧

（武汉大学 物理科学与技术学院，湖北 武汉430072）

现有的频率域波全形反演多是默认基于正方形旋转交错网格，而基于矩形旋转交错网格的全波形反演有更大的灵活性，能更好地适应实际地下介质结构，有更好的内存使用率和计算效率。为了解决原始的基于正方形网格的PML（完全匹配层）吸收边界形式不再适用的问题，文中将通过声波方程完全匹配层吸收边界的经典方法，构建并推导出PML吸收边界条件在矩形旋转交错网格中的具体形式，通过Marmousi模型正演和反演实验，得出本文所构建的PML边界获得良好的吸收效果，对反演结果有很好的改善。

频率域全波形反演；矩形旋转交错网格；正演；完全匹配层

频率域全波形反演是在时域波形反演的基础上发展起来的，经过Marfurt[1]、Shin[2]、Worthington[3]、Pratt[4-5]等进一步地深入研究与完善，利用频率域全波形反演的方法来重建地下介质结构，越来越受到人们的关注。与时域全波形反演相比，频域全波形反演计算效率更高，能处理更大的地下介质模型，有更好的实用性。

交错网格最早由Madariage[6]提出，Pratt改进了经典五点有限差分法求解波动方程，Jo[7]等人提出了九点旋转交错网格有限差分法来提高拉普拉斯域和质量加速项的精度[8-9]。而这些方法是基于正方形网格的，这样造成的影响是在一些领域无法适应地下结构，同时可能增加不必要的内存和计算量，这对于大模型全波形反演是一个难点。而实际地下介质结构，横向速度变化较小，纵向速度变化较大，基于矩形网格的全波形反演有更大的灵活性，能更好地适应实际地质结构，同时可减少网格点数目，有更好的内存使用率和计算效率。

在实际地震勘探中，地震波在地下是无限传播的，而在我们波场模拟的过程中，由于计算机存储的限制，在我们所需研究的区域外，加入了人为的截断边界。地震波会在人为边界上产生反射，反射回的波会产生新的波场，对我们预期的波场产生干扰。因此，需要引入吸收边界条件，消除人为截断边界的影响。现在应用最广泛的人工边界条件是Berenger提出的完全匹配层法[10]，有着比较理想的吸收效果。其基本思想[11]是，在模拟区域周围添加完全匹配层，在完全匹配层中加入吸收衰减因子，吸收人为截断边界差生的反射波。

在矩形旋转交错网格频率域全波形反演中，随着矩形网格宽长比的变化，原始的基于正方形网格的PML边界形式已经不再适用。因此，文中从声波方程完全匹配层吸收边界的经典方法出发，构建并推导出PML边界条件在矩形旋转交错网格中的形式。在原矩形旋转交错网格频域全波形反演算法的基础上，添加文中所构建的矩形旋转交错网格中的PML边界条件，以Marmousi模型为目标模型，通过正演和反演实验，表明文中所提方法的有效性。

1 方法原理

1.1 一般网格PML层声波方程的离散形式

二维线性标量声波方程形式如下[12]：

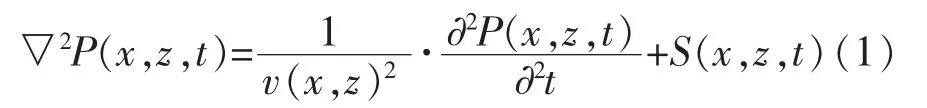
式中P（x，z，t）为模型中（x，z）点处的声波波场，v（x，z）为模型中（x，z）点处的介质速度，S（x，z，t）为时域震源，∇2为拉普拉斯算子。

为简单起见，不考虑PML层中震源S的作用。按照经典PML边界的理论[13]，将波场P分裂为两项，即P=Px+Pz，通过引入中间变量、加入衰减因子，可构造如下PML吸收边界条件：

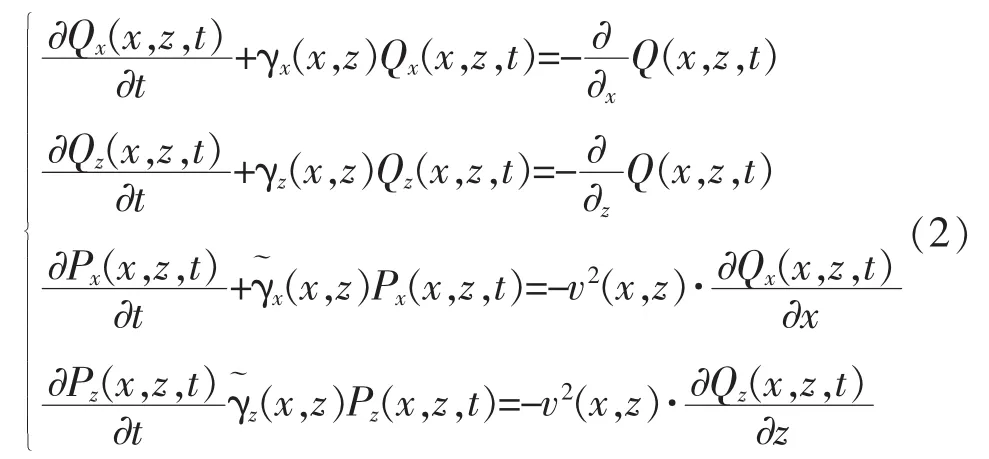
式中Q为中间变量，γ为PML层衰减系数。再将将式（2）变换回频域、差分离散、消去中间变量、合并，可推出一般网格PML层声波方程的离散形式为：

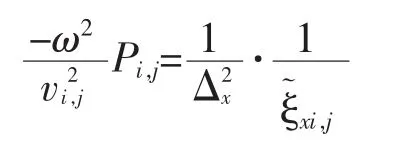
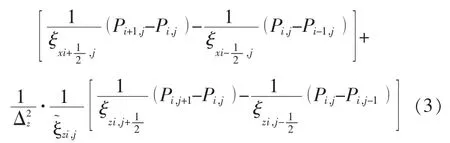
式中Δx为横向网格间距，Δz为纵向网格间距，ξ=1+iγ/ω。

1.2 矩形旋转交错网格中PML边界的构建

矩形旋转交错网格的基本思路如图1所示，对任意点和其8邻域点进行有限差分，将微分形式近似转换为差分形式，对声波方程进行离散，然后求解离散后的声波方程。如图2所示，里面包含两种坐标系，一种是直角坐标系，另外一种是旋转后的坐标系。

图1 矩形网格示意图

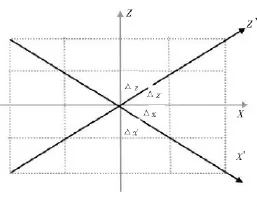
图2 旋转坐标系示意图

矩形旋转交错网格PML边界的构建分为3个部分：一是旋转坐标系，推导出声波方程在新旋转坐标系下的具体形式；二是参照经典PML边界的构建方法，推导出新旋转坐标系下的离散形式；三是将原正交坐标系和新旋转坐标系下的PML边界混合加权，融合生成矩形旋转交错网格下的PML边界。

旋转后坐标系x′z′下的坐标与原正交坐标系xz下的坐标关系为：

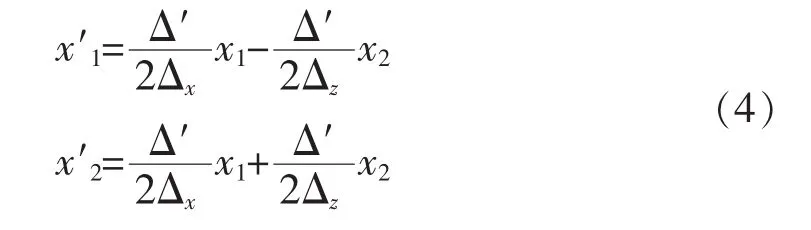
对（4）式两边求二阶微分并整理可得：

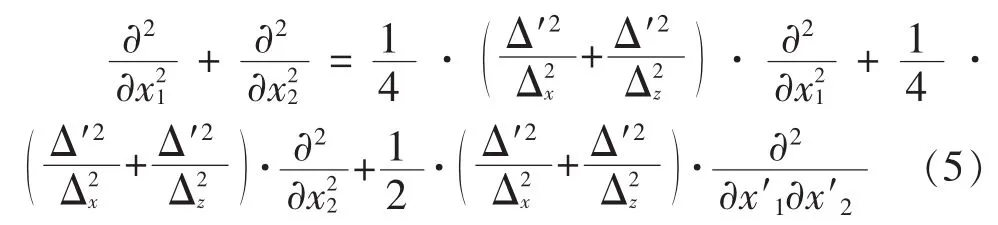
由（1）（4）式可以得出旋转后新坐标系x′z′下的声波方程为：

与构建一般网格PML边界同样的过程，可推导出旋转新坐标系x′z′下PML层声波方程的离散形式为：

设原正交坐标系xz下的PML层所占比重为η，新旋转坐标系x′z′下的PML层所占比重为1-η，构建权重因子如下：

将式（3）、（6）分别乘以η和1-η，即可将两个坐标系下PML层声波方程按权重融合即可得到矩形旋转交错网格中PML层的离散形式。至此，矩形旋转交错网格中PML边界的离散形式构建完毕。

2 算法数值实验

为了验证文中提出的基于矩形旋转交错网格PML边界的有效性，文中将以Marmousi模型进行基于矩形旋转交错网格的频域全波形反演实验，从正演和反演结果两个方面进行说明。在算法实现过程中，软件平台使用Visual Studio 2010，运行环境为64位windows7操作系统，编程语言是C++，在处理线性方程组时调用MUMPS[14]库来进行求解。

Marmousi模型横向距离范围为0～9 200米，横坐标网格间距为12.5米，共737个网格；纵向深度0～3 000米，纵坐标网格间距12.5米，共240个网格。为将Marmousi按矩形网格划分，文中对Marmousi模型的纵向距离进行线性插值，在不改变整个模型大小的情况下，将模型纵坐标网格间距减少到10米，纵向网格数目变为360。炮点共240个，分布于地表，炮点覆盖范围分布于模型的横坐标从3 000米到8 975米处，炮间距25米。每个炮点的接收点均分布于该炮点左侧，最大炮检距（炮点和接收点之间的距离）为2 575米，最小炮检距200米，道间距25米，每个炮点有96个接收点，即96道。

2.1 正演实验

正演是利用初始速度模型得到模拟波场记录，是反演的前提和基础。文中初始速度模型选取匀速递增模型。正演的采样时间为3 s，采样间隔为4 ms，共750个采样点。震源为Ricker子波，主频为8 Hz。

以Marmousi模型第一炮的数据为例，第一个炮点位于地表3 000米处，96个接收点分布在425～2 800米间，即接收道的第1个接收点位于425米处，第96个接收点位于2 800米，中间94个检波点平均分布于此区域内。分别记录无PML层和添加本文所构建的PML层（20层网格厚度）时，第一个炮点正演的波形记录，其中横坐标表示96个接收点的道号，纵坐标表示采样时间。

图3（a）显示，当原原矩形旋转交错网格频域全波形反演算法不添加PML吸收层时，在边界处反射现象明显。由于正演是反演的前提和基础，正演结果的精度将在很大程度上影响反演结果，所以边界处产生的反射必将对反演过程带来很大的干扰。图3（b）显示，加入文中所构建的PML层后反射现象得到明显抑制。由此可见，文中所构建的PML边界取得了良好的吸收效果，这也将会对反演结果带来积极影响。

2.2 反演实验

反演是建立理论波场与模拟波场之间残差的目标函数，通过使目标函数极小来更新速度模型，是一个对目标函数最优化的问题。文中使用的是预处理梯度算法[15]。

图3 Marmousi模型第一个炮点正演模拟的波形记录

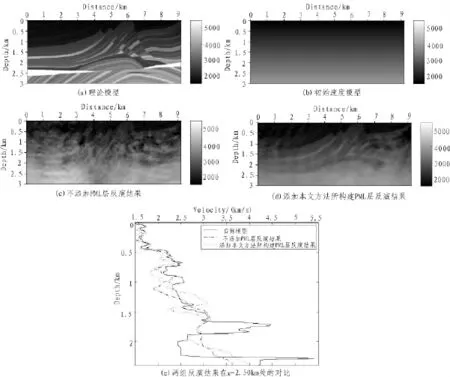
图4 Marmous模型的频率域全波形反演

图4 （c）和4（d）分别为不添加PML层和添加文中所构建PML层反演结果的反演结果，可以看出添加本文所构建的PML层后，反演结果整体上结构更清晰。图4（e）给出了在水平距离左边界2.50 km处，两组结果的对比，可以看出添加本文构建PML层的反演结果，速度分布更接近理论模型。这是由于PML层很好地吸收了地震波在人工边界处的反射，减少了反射波的干扰，实验结果更精确，从而更接近理论模型，这与正演的实验结果也相符合，由此可以验证文中所提算法的有效性。

3 结束语

文中构建并推导出PML边界在矩形旋转交错网格中的形式，通过正演和反演实验，验证其对人为边界处的反射波有很好的吸收效果，对最终的反演结果也有很好的提升。另外，由于本文在选取PML层衰减因子时，沿用了正方形网格PML层衰减因子的形式。而随着矩形网格宽长比的变化，构建新的衰减因子也是一个值得研究的方向。

[1]Marfurt K J.Accuracy of finite difference and finite element modeling of the scalar and elastic waveequations[J].Geophysics，1984，49（5）:533-549.

[2]Shin C S.Nonlinear elastic wave inversion by blocky parameterization [D].Tulsa，Oklahoma，United States:University of Tulsa，1988.

[3]Pratt R G，Worthington M H.Inverse theory applied to multi-source cross-hole tomography.Part I:Acoustic wave-equation method[J].Geophys Prosp，1990，38（3）:287-310.

[4]Pratt R G.Inverse theory applied to multi-source cross-hole tomography， PartII:Elastic waveequation method[J].Geophys Prosp，1990，38（3）: 287-310.

[5]Pratt R G.Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging[J].Geophysics，1990，55（5）:626-632.

[6]Madariaga R.Dynamics of expanding circular fault [J].Bulletin of the Seismological Society of America，1976，66（3）:639-666.

[7]Jo CH，Shin C，Suh JH.An optimal 9-point，finite-difference，frequency-space，2-D scalar wave extrapolator[J].Geophysics，1996（61）：529-537.

[8]Erik H S，Norbert G，Serge A S.Modeling the propagation of elastic waves using a moodified finitedifference grid[J].Wave Motion，2000（31）:7-792.

[9]Reeshidev B，Mrinal K S.Finite-difference modeling of S-wave splitting in anisotropic media[J]. Geophysical Prospecting，2008（56）:293-312.

[10]Berenger J A.perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics，1994（114）:185-200.

[11]Hastings F D，Schneider J B，Broschat S L. Application of the perfectly matched layer（PML）absorbing boundary condition to elastic wave propagation[J].Journal of the Acoustical Society of America，1996，100（100）:3061-3069.

[12]Bjorn Engquist.Computationalhigh frequency wave propagation[J].Acta Numerica，2003:181-266.

[13]Collino F，Tsogka C.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J].Geophysics，2012，66（1）:294-307.

[14]Solver.MUltifrontal Massively ParallelSolver（MUMPS 4.10.0）Users guide[R].French:MUMPS，2011.

[15]Operto S，Virieux J，Dessa J X，et al.Crustal imaging from multifold ocean bottom seismometers data by frequency-domain fullwaveform tomography: Application to the eastern ankaiTrough[J].Journal of Geophysical Research，2006，111（B9）：171.

Research and implementation of the PML boundary conditions based on rotated rectangular-grid modeling method

ZHANG Liang，SUN Jin-yao
（School of Physics and Technology，Wuhan University，Wuhan 430072，China）

The present Frequency-domain full waveform inversion（FWI）is mostly default to a rotated square-grid，but the FWI based on rotated rectangular-grid is more flexible，and can better adapt to the actualstructure ofunderground media，and have greateradventage in memory utilization and computational efficiency.To overcome the problem that the original square-grid PML（Perfectly Latched Layer）absorbing boundary conditions no longer apply，the paper give the new form of PML absorbing boundary conditions based on rotated rectangular-grid through the classic building strategy.Using the forward modeling and inversion experiment with Marmousi model，we show that the proposed PML boundary in this article can obtain satisfactory absorbing effect，and improve the inversion result.

frequency-domain full waveform inversion；rotate rectangular-grid；forward modeling；PML

TN91

：A

：1674-6236（2017）02-0163-05

2016-04-12稿件编号：201604110

大型油气田及煤层气开发国家科技重大专项课题（2011ZX05003-003）

张 亮（1991—），男，湖北枣阳人，硕士。研究方向：二维地震波频率域全波形反演。