基于哈希树的度量证据可信存储方案设计

邴丕政 戴紫彬 戴 强

(解放军信息工程大学密码工程学院 河南 郑州 450001)

基于哈希树的度量证据可信存储方案设计

邴丕政 戴紫彬 戴 强

(解放军信息工程大学密码工程学院 河南 郑州 450001)

计算平台的可信性由远程证明过程中提供的度量证据进行验证，验证程序根据计算平台在启动过程创建的度量证据建立信任。度量值扩展操作创建的度量证据和相关度量记录是线性的，查找效率较低。提出一种基于平衡二叉哈希树的构建度量证据的方法。计算平台上组件的度量值作为树叶，所有组件的度量值集合的度量值作为树根。在验证计算平台的过程中，使用哈希树的度量记录和根寄存器，在度量证据与标准值比较时显著提高错误组件查找的速度，从而提高效率。实验结果表明，平衡二叉哈希树模型在不增加空间复杂度的同时，查询时间开销显著减少。

平衡二叉哈希树 远程证明 错误定位 可信计算

0 引 言

计算平台启动期间，BIOS、bootloader、操作系统、应用程序等组件都需要经过计算平台的度量，一级信任一级地产生信任链。组件度量值由组件代码和配置数据经过计算平台的哈希运算产生，并存储在平台配置寄存器PCR(Platform Configuration Register)中，其存储状态受到保护。在对PCR进行扩展的同时，组件在存储度量日志SML(Storage Measurement Log)中记录度量中间步骤的度量值和度量事件，不需要保护措施。安全启动完成后，度量值作为度量证据唯一确定平台的可信状态。

基于完整性度量架构，每个组件均包含一个完整性参考清单RM(Reference Menu)结构，该结构提供组件的完整性参考值。远程证明中的相关对象需要加密存储。平台上使用身份认证密钥AIK(Attestation Identity Key)对当前存储的PCR值进行签名，然后报告平台状态。在进行平台验证时，SML与相关PCR的值同时交给验证平台进行验证，验证平台首先根据PCR的值验证SML的可信性，再根据SML查找相应的RM结构，通过比较SML提交的平台度量证据与RM结构中的参考信息进行评估，得出验证结论。SML的线性结构决定了其在灵活性和效率上的局限性。Schmidt等[1]提出的改进默克尔哈希树模型来进行平台的远程证明，其模型的构建基于满二叉树，空间利用率不高。李俊中[2]提出以默克尔哈希树模型作为完整性验证方案，通过数据块签名及标签绑定，完成动态的数据操作。但是实际应用中需要进行频繁的数据填充操作，其满二叉树的结构也易造成额外空间开销。朱毅等[3]提出以非平衡二叉树为基础改进哈希树模型，其节点数量动态增加，空间利用率高。该模型上的节点查找操作性能不佳。

本文提出一种方案，通过平衡二叉哈希树构造度量证据的数据组织方式，同时扩展SML。该数据结构在度量证据与标准值比较时定位错误组件的效率更高，并且允许动态增加组件以进行更高效的验证。同时该结构增加了每一点上的可扩展性，其灵活性大大增强。

1 基于线性链的度量证据

1.1 线性链及其产生步骤

度量证据存储在TPM的PCR中，受到平台保护，在TPM中仅由授权指令访问。TPM通过扩展操作规定度量证据的计算方法，其本质是构造线性顺序的内嵌哈希值链，计算过程如下：

Vi(k)=H(Vi(k-1)‖mk)

其中，Vi表示平台配置寄存器(i=0,1,…,23)，H是抗碰撞哈希函数(TPM中以SHA1为例实现)，mk的值是数据的哈希值，顺序启动过程的第k个度量值。扩展操作在TPM安全执行环境的内部执行。在原值的基础上进行扩展操作，如果被度量的数据发生变化，运算出的度量值将会发生变化。这种机制可判断并保障平台状态信息是否可信，将PCR结果和SML一同比较，可验证平台是否有新的进程注入，同时也能发现攻击者的恶意攻击。图1表示平台配置寄存器的线性链结构，由扩展操作产生，最终状态由PCR记录并保护。

图1 线性链扩展

1.2 错误定位

验证程序比较SML的每个度量证据和相关组件的标准值，若度量证据与标准值不同，表示相应组件的错误。线性链度量证据的错误组件定位需要追踪度量证据的位置，即当SML包含N个度量证据时，至少需要计算复杂度为N的扩展操作(PCR值的SHA1操作)和对标准值的N次搜索，以确定被修改的度量证据的位置。

2 平衡二叉哈希树度量证据

线性链度量证据在查找上的局限性，使得由线性链扩展操作构建的度量证据对平台远程证明和组件修复等高级管理功能都有局限性。实际的SML存储空间有大量组件的度量证据，若是以线性搜索的方法筛选错误的组件，代价昂贵且效率较低。

平台度量证据的处理需要满足：(1) 度量证据包含足够多的信息，允许计算平台提供独立的、受密码保护的度量证据，保证度量证据在传递过程中的可信，防止证据被篡改或者泄露；(2) 计算平台的标准值对验证平台而言是可获得的，既要保证标准值的机密性，又要保证其授权访问。

2.1 哈希树度量证据的构建

为了使构造算法尽可能简洁高效，提供错误组件的快速查询功能，本解决方案采用平衡二叉哈希树进行构造。树叶节点携带组件的度量证据，树根的度量证据是整个平台的度量证据的集合，存储于PCR；非树叶节点携带的度量证据存储在SML中。SML组织度量证据的数据结构支持标准树的操作和遍历。平台验证期间，SML支持新叶子的顺序增加并保持左右子树的关系。在深度为d的树的叶子上增加新的度量证据，需要重新计算所有深度为d-1的树叶的内部节点的度量证据。

平衡二叉哈希树的构造必须满足如下条件：(1) 哈希树的左子树和右子树的深度之差的绝对值不超过1；(2) 哈希树的左子树和右子树也是一颗平衡二叉哈希树。树中每个节点的信息包括节点的左子树、结点的右子树、节点的度量证据、节点的深度。经过分析得出，自下而上构造平衡二叉哈希树的算法如下所示。

node_t insert_node(node_t)

R、B、M newnode();

M->left = R;

M->right = B;

M->data = measure(R->data,B->data);

//构造初始最简二叉树

While(Vi != NULL)

//度量值成功写入时向二叉树中添加节点

Mi = newnode();

Mi->left = M;

Mi->right = Vi;

Mi->data = HASH(M || Vi);

//新添加节点的信息填充

if(Height(Mi->left) - Height(Mi->right) ==-2)

//树出现不平衡，需要左旋转的情况

M = LeftRotate(Mi);

else if(Height(Mi->left) - Height(Mi->right)==2)

//树出现不平衡，需要右旋转的情况

M = RightRotate(Mi);

M->height = MAX( Height(M->left)，Height(M->right) ) + 1;

//重新计算树的平衡度

remeasure(M);

//重新计算整棵树的节点度量值

return M;

其中，Vi表示存放组件度量证据的寄存器，初始化为NULL。自下而上地构建基于度量证据的平衡二叉哈希树的步骤如下。

第一步 每一个组件的度量证据均存放在PCR中，两个组件完成度量，将它们的度量证据进行扩展，动态添加新的树节点并存放其中，令新节点为两个组件叶子节点的父亲。因此构造出一棵最简单的基于两个组件度量证据的平衡二叉哈希树。如图2所示。

图2 平衡二叉哈希树的构造过程

第二步 当有其他组件度量完成时，将其证据跟最新的扩展证据进行扩展，生成的扩展证据作为最新的树的根。此时需要注意，若破坏了平衡二叉哈希树的条件之一导致树的不平衡，需要进行节点的旋转。涉及到的旋转类型包括左旋转和右旋转。其中右旋转的具体操作如图3所示。

图3 调整树平衡的右旋转操作

经过多次旋转，最终达到构造平衡二叉哈希树的两个条件即可。

第三步 旋转完成后，重新计算非叶子结点的中间度量证据。最终生成的树中，其树根是所有组件的度量证据的集合后的哈希root_hash，中间节点是组件之间度量证据的集合后哈希，树叶是单个组件的度量证据。

2.2 远程证明步骤

计算平台在进行远程证明行为时，遵循可信计算规范，加入TPM签名步骤。流程及步骤如图4所示。

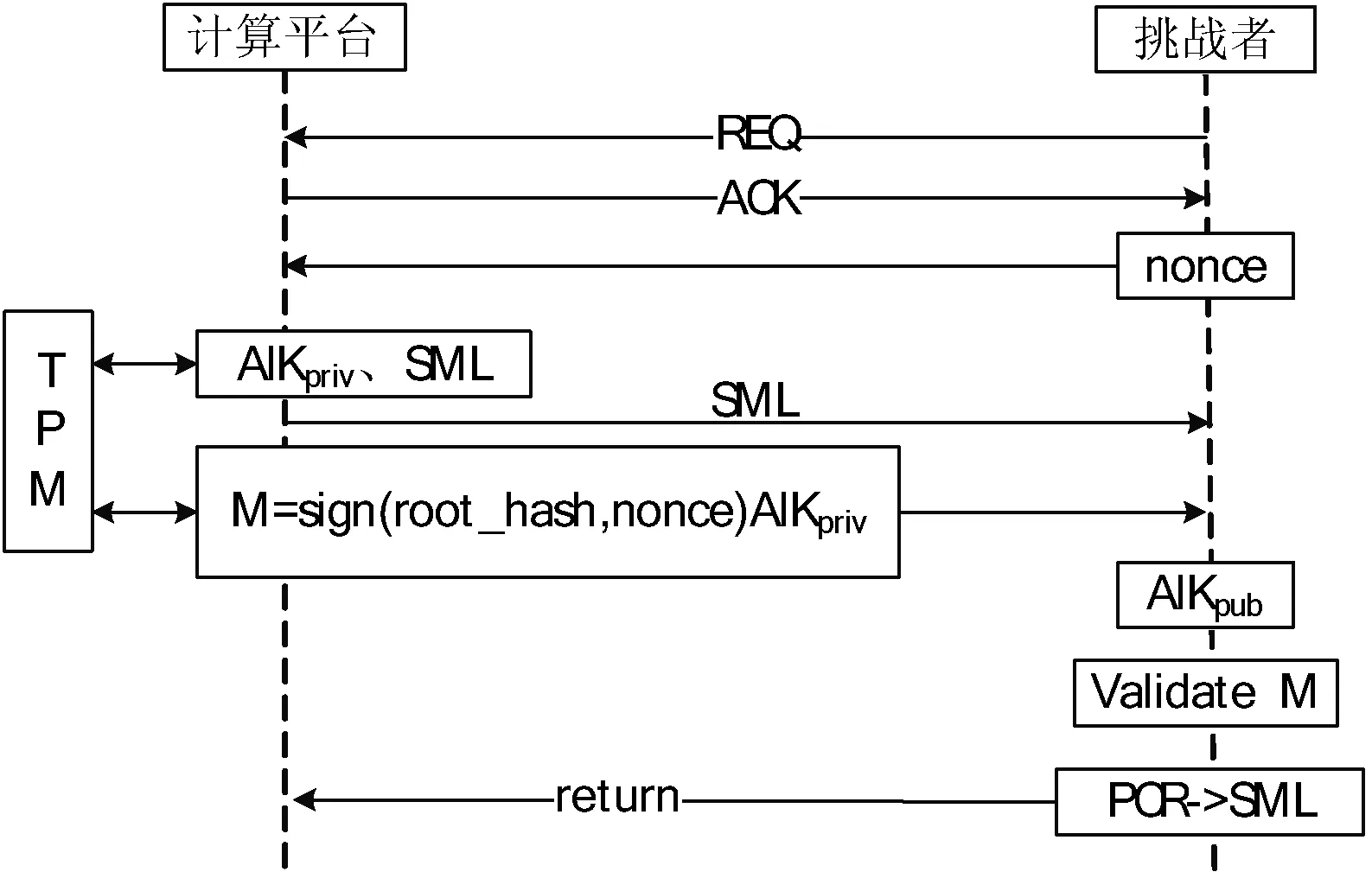
图4 远程身份证明流程

(1) 计算平台及挑战者进行挑战—应答。

(2) 挑战者生成160 bit的随机数nonce，用于避免重放攻击，并将该随机数传给计算平台。

(3) 计算平台从TPM产生的受保护的根密钥SRK中获取用于签名的AIK私钥，并对root_hash和nonce进行加密签名；获取SML。计算平台发送数据包给挑战者，该数据包包含对nonce和SML的签名和AIK的公钥。

(4) 挑战者验证AIK证书和签名，获得root_hash和SML值，处理SML并重新计算接收的PCR值，比较这两个值是否匹配，检査SML是否有效并且是否受到攻击。

(5) 若匹配，说明计算平台处于可信状态；若不匹配，计算平台验证身份失败，需要定位错误的组件构成的子集。

验证程序从树根开始查找。在采用深度优先搜索遍历整棵树的过程中，会产生度量证据跟标准值不同的组件的叶子节点集合。节点的值跟标准值作比较，不相等则说明其子树的树叶代表的组件已经被破坏，继续针对其子节点继续比较直至树叶；相等则说明其子树的树叶代表的组件完整性经过验证，停止比较。结果标记为g表示一致，标记为b表示不符。结果标记用图5表示。

图5 错误定位标记结果

在图5(a)中，父节点及其子树通过度量证据的验证，遍历该节点的叶子节点，表示平台组件的完整性没有受到恶意篡改，平台是可信的。在图5(b)中，验证程序计算父节点与度量证据比较失败，向下遍历到子节点的值，并比较子节点的完整性。通过这种方式，验证过程向下遍历到下一个树层，通过错误的度量证据找到子树的树叶、左树叶、右树叶或者左右树叶。

3 构造树的复杂度分析

首先考虑构造平衡二叉哈希树算法的空间复杂度。平衡二叉哈希树的构造需要考虑两个关键的因子：树的深度、树的叶子节点数。考虑最坏情况，即平衡二叉哈希树是一个完全填充的深度为h的满二进制树，含有2h-1个节点，均存储在SML。在这种情况下，哈希树SML的存储空间约为两倍的线性链SML存储空间大小，即符合下列等式：

2h-1≈2h-1×2

考虑到两种方案的PCR都只存储树叶的度量证据，中间节点的度量证据中间值只存储在SML中，这样的空间开销是可接受的。

然后考虑时间复杂度。在平衡二叉哈希树上的遍历工作，其遍历过程中和给定标准值进行判定的关键字个数不会超过树的深度。假设深度为h的平衡二叉哈希树含有的最大节点数为Nh。显然有：

N0=0N1=1N2=2

且有下式成立：

Nh=Nh-1+Nh-2+1

利用归纳法和斐波那契序列性质容易证明：当h≥0时，含有n个节点的平衡二叉哈希树的最大深度为：

因此，在平衡二叉哈希树上进行查找的时间复杂度为O(logn)。

4 实验及分析

为在实践中验证该方案的可行性，在CentOS6.4系统下搭建以开源项目TPM-Emulator为硬件TPM模拟环境，IBM开源软件TrouSerS为软件基础环境的实验平台，经过源代码的修改实现计算平台的TCM软件栈。实验环境如表1所示。

表1 实验环境

TPM调用TPM_TREE_EXTEND作为平衡二叉哈希树构造的命令，其输入与原构造线性链的命令TPM_EXTEND相同。TPM利用PCR的标记指明当前二叉树的树根，其值为度量证据的中间结果。TPM_TREE_EXTEND命令的返回值为更新过的度量证据，按序排列。树构造成功时得到的最终的度量证据代表平台的可信。

为了测试构造平衡二叉哈希树算法的性能，将任意的160bit的数据作为TPM_TREE_EXTEND命令的输入。我们假定这些人工生成的输入作为测试用例的度量证据。使用函数SystemNanoTime对执行时间进行计算。输入的度量证据分别为215、217、219，从处理器频率为2.53GHz的系统开机引导模拟开始执行。实验得出的信任链构造的时间曲线如图6所示。

图6 构造时间比较

由图6的结果表明，在线性链结构的PCR度量值扩展操作过程中，每进行一次扩展，算法只需要进行数据的线性变换，所耗时间基于数据量的大小呈线性关系；在二叉树树式结构的度量值扩展操作过程中，每进行一次扩展，算法需要进行树的旋转操作、树的遍历操作、重新计算除了树叶之外的所有非树叶节点的中间度量数据结果，因此时间基于数据量的大小呈现上升趋势。

线性链的查找时间和平衡二叉哈希树的遍历时间的比较如图7所示。

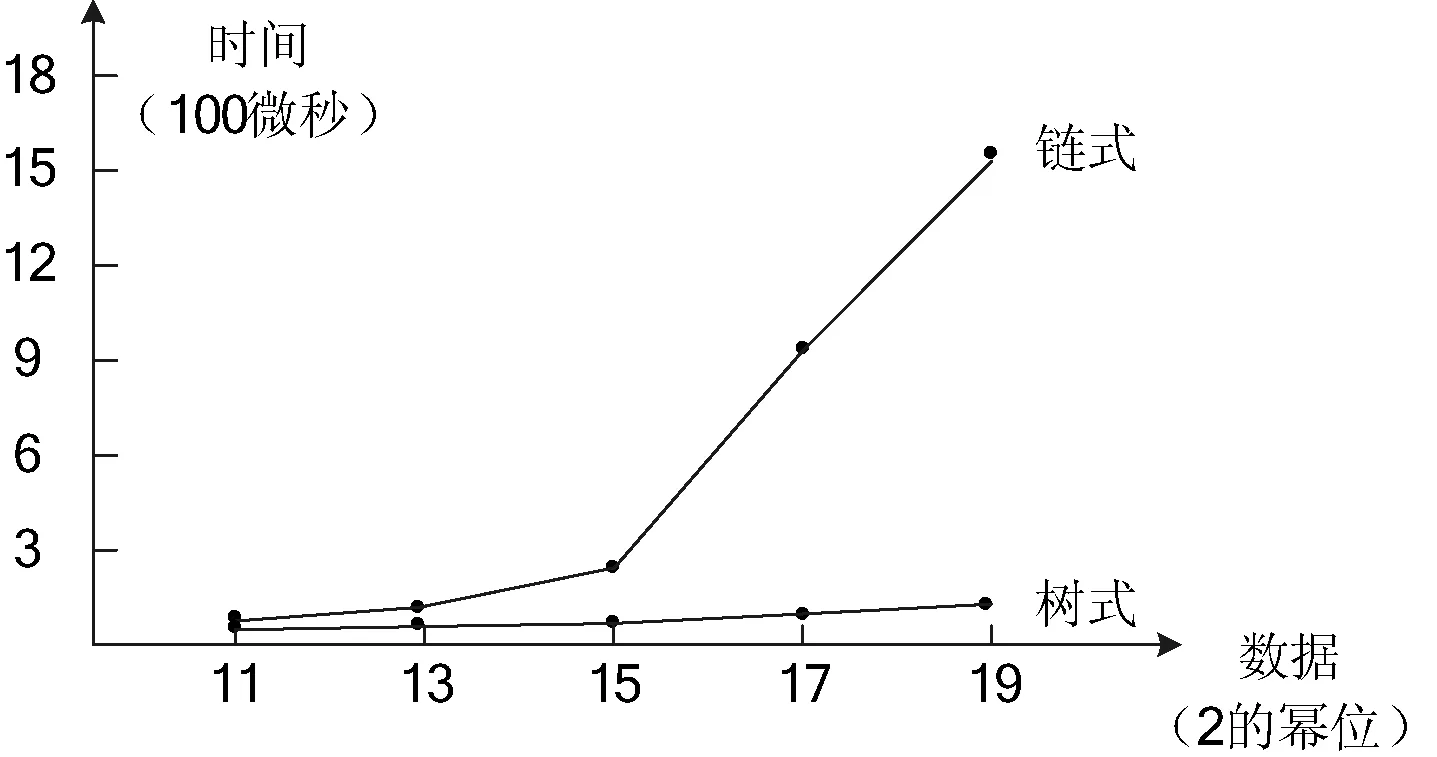
图7 查找时间比较

图7结果表明，当验证失败，需要定位错误的时候，线性链结构的查找采用顺序查找，时间消耗基于数据量的大小逐渐升高；平衡二叉哈希树的遍历采用先序遍历，遍历的时间跟树的高度相关。随着数据量的增加，树的高度较好地维持在O(logn)，查找时间也相对稳定。因此组件的度量证据数据量越庞大，平衡二叉哈希树表现出来的查找优势越明显。

5 结 语

本文在总结了度量证据生成过程中线性链机制错误组件查找效率不佳的基础上，利用二叉树搜索时间复杂度为对数级的特性，构造了以平衡二叉哈希树为数据组织形式的度量证据可信存储方案，实现了查找效率上的提升。最后搭建实验平台，给出链式和树式的度量证据构造和查询的时间对比。结果显示该方案的空间复杂度保持在O(n)情况下，查找时间大大减少，性能大大提升。

[1]AndreasUSchmidt,AndreasLeicher,AndreasBrett,etal.Tree-formedVerificationDataforTrustedPlatforms[J].ComputersandSecurity,2012,4(18):1-15.

[2] 李俊中.云存储环境下数据完整性验证方法研究[D].重庆:重庆邮电大学,2013.

[3] 朱毅,李清宝,钟春丽,等.用于细粒度完整性度量的非平衡二叉哈希树模型[J].小型微型计算机系统,2014,7(35):1604-1609.

[4]SchmidtAU,LeicherA,ChaI,etal.Trustedplatformvalidationandmanagement[J].InternationalJournalofDependableandTrustworthyInformationSystems,2010,1(2):1-31.

[5] 王防修,周康.一种构建严格平衡二叉搜索树的非递归算法[J].武汉工业学院学报,2013,32(4):32-34.

[6]SchmidtAU,LeicherA,ChaI.Scalingconceptsbetweentrustandenforcement,in:Z.Yan(Ed.),TrustModelingandManagementinDigitalEnvironments:FromSocialConcepttoSystemDevelopment[J].IGIGlobal,Hershey,2010,2(54):20-57.

[7] 中国国家密码管理局.可信计算密码支撑平台功能接口与规范[EB/OL].[2011-02-19].http://www.oscca.gov.cn/Doc/6/News_1132.htm.

[8] 王江,少余综,李光.可信计算之信任链技术研究[J].计算机工程与设计,2008,29(9):2195-2198.

[9]SailerR,ZhangX,JaegerT,etal.DesignandimplementationofaTCG-basedintegritymeasurementarchitecture[J].Proceedingsofthe13thUSENIXSecuritySymposium,2004,7(31):223-238.

[10]ElbazR,ChampagneD,GebotysC,etal.Hardwaremechanismsformemoryauthentication:Asurveyofexistingtechniquesandengines[J].TransactionsonComputationalScience,2009,4(5430):1-22.

THE DESIGN OF CREDIBLE STORAGE SCHEME ON MEASUREMENT EVIDENCE BASED ON HASH TREE

Bing Pizheng Dai Zibin Dai Qiang

(InstituteofCryptographicEngineering,People’sLiberationArmyInformationEngineeringUniversity,Zhengzhou450001,Henan,China)

The credibility of computing platform is verified by the measurement evidence provided in the process of remote attestation procedure, and the verification procedures build trust according to the measurement evidence which is created in the startup process of the computing platform. However, the measurement evidence and the associated measurement record which are created by extended operation of measurement are linear, with a low researching efficiency. Thus, a method of creating measurement evidence is proposed based on balanced binary hash tree. On the computing platform, the component measurement values are represented as leaves, and the set of measurement value of all components are represented as the roots of a hash tree. In the process of verifying computing platform, the hash tree measurement records and the root registers are used to increase the searching speed of fault component when the measurement evidence is compared with the standard value. The experimental results show that the proposed model reduces time cost without increasing space complexity.

Balanced binary hash tree Remote attestation Fault localization Trusted computing

2015-11-04。邴丕政，硕士生，主研领域：信息安全。戴紫彬，教授。戴强，博士。

TP309

A

10.3969/j.issn.1000-386x.2017.01.057