改进的人工蜂群优化支持向量机算法在入侵检测中的应用

刘 铭 黄凡玲 傅彦铭 杨晓玲

1(安阳工学院计算机科学与信息工程学院 河南 安阳 455000)2(清华大学软件学院 北京 100084)3(广西大学计算机与电子信息学院 广西 南宁 530004)

改进的人工蜂群优化支持向量机算法在入侵检测中的应用

刘 铭1黄凡玲2傅彦铭3杨晓玲3

1(安阳工学院计算机科学与信息工程学院 河南 安阳 455000)2(清华大学软件学院 北京 100084)3(广西大学计算机与电子信息学院 广西 南宁 530004)

针对基于传统的参数优化算法在优化过程中会不同程度地陷入局部最优解的问题，在人工蜂群ABC(Artificial Bee Colony)算法的基础上提出基于交叉突变人工蜂群CMABC(Crossover Mutation ABC)算法的支持向量机SVM参数优化方法，并将其应用于入侵检测。通过引入交叉突变算子对人工蜂群算法进行改进，根据适应度值的优劣将蜂群进行划分，有效地避免了陷入局部最优，提高了收敛速度。利用标准测试函数验证了算法的有效性，并采用NSL-KDD入侵检测数据集进行仿真实验，验证了该方法的有效性。实验结果表明，该方法能有效提高入侵检测的分类性能。

入侵检测 支持向量机 人工蜂群算法 交叉突变算子

0 引 言

随着网络规模的日益扩大，计算机网络为人们生活和工作带来便利的同时，网络入侵技术和攻击手段也更加复杂，各类破坏性的网络攻击所造成的损失日益严重，网络安全威胁也日益增长。传统单一的安全防御方法和策略虽然在一定程度上对网络安全起到了保护作用，但已经无法防范复杂多变、日益猖獗的入侵行为。于是产生了网络安全的第二道防线——入侵检测系统IDS(Intrusion Detection System)。

入侵检测技术通过在计算机网络系统的关键节点上收集信息并进行分析，对系统中违反安全策略的行为及时作出响应。网络入侵检测中的数据非常庞大复杂，具有高维、小样本、线性不可分的特性[1]。支持向量机SVM作为一种在小样本机器学习的基础上发展起来的方法，通过风险最小化原理来解决小样本、非线性、高维度等问题，并且能够在先验知识不足的情况下仍然保持较高的分类准确率，非常适合应用于网络入侵检测系统。

SVM分类算法中惩罚因子和核参数的选取直接影响到支持向量机的分类精度及它的推广性能。传统的用于SVM参数优化的算法有经验法[2]、遗传算法[3]、梯度下降法等，这些传统的参数优化算法在优化过程中会不同程度陷入局部最优解，不能建立有效的SVM最优分类模型。

人工蜂群ABC算法是Karaboga在2005年提出的一种新的群智能优化算法[4]。它具有参数少、实现简单等优点。多项实验结果表明，该算法通过模拟蜂群采蜜的过程，在解决参数优化问题时表现出一定的优势，但存在对单峰问题收敛过慢，对于多峰问题易于陷入局部最优解的问题。针对这些问题不少学者也提出了一些改进方法，刘俊芳等提出PSO和ABC的混合优化算法[5]，Zhu等通过引入全局最优解提出GABC算法[6]，以期提高收敛速度。这些优化算法改进了算法的收敛速度，但仍旧会不同程度的陷入最优解，特别是对多峰优化问题。而研究表明，SVM的正确分类率与惩罚因子、核函数参数之间存在多峰函数关系[7]。为了获得更好的参数来提高SVM的分类性能，本文采用交叉突变的思想对ABC算法做进一步的优化，将交叉突变算子引入到不同的子种群之间，改进了ABC算法在优化多峰问题时过早陷入局部最优的缺点。将改进后的ABC算法和ABC算法、GABC算法和受鸟觅食的行为启发的粒子群优化算法PSO(Particle swarm optimization)[8]进行收敛性分析，并将几种算法分别应用于基于SVM的入侵检测中进行实验对比，采用NSL-KDD网络入侵检测数据集对改进的ABC算法的有效性进行检验。

1 支持向量机

1.1 SVM原理

SVM的基本原理是将输入向量通过预先选取的非线性关系映射到一个高维的特征空间，并在此空间寻找一个最优分类超平面，使两类的分类间隔最大。假设有训练数据：

(x1,y1),(x2,y2),…,(xn,yn)x∈Rny∈(+1,-1)

超平面记为 (w·x+b)=0

(1)

为了构造最优分类超平面，求分离间隔最大可转换为如下的优化问题：

s.tyi[(w·xi+b)]-1+ξi≥0i=1,…,n

(2)

松弛变量ξi≥0，C为大于零的常数，它决定了对错分样本的惩罚力度[9]。引入Lagrnage乘子αi将其转换为对偶问题：

(3)

求解上述二次规划问题可得到最终的决策函数：

(4)

1.2SVM参数影响分析

结合RBF径向基核函数具有收敛域较宽，有较好的非线性映射能力等优点，本文将其作为支持向量机分类器的核函数，以惩罚因子C和核参数g为对象建立SVM模型参数优化方法。这两个参数的选取直接影响到支持向量机的分类精度及其推广性能。惩罚因子C用来平衡特征子空间中SVM的置信范围与经验风险之间的比例[10]，在确定的特征子空间中，C的值越小代表对经验误差的惩罚力度越小，造成模型的训练误差越大，经验风险值也越大，这时得到的模型预测结果分类错误率也就较高，出现“欠学习”的现象。同理，当C的值过大时就会出现“过学习”的现象。

核参数与核函数密切相关，当核函数确定时，相应的映射函数和特征空间也就确定。核参数g的选取将直接影响到核函数的特性，致使样本数据在高维特征空间中的分布复杂程度发生变化，即高维特征空间的维数，过大过小都不能保证结构风险最小化。

因此，在每个特征子空间中，都有一个合适的惩罚因子C和相应的核参数g使SVM的推广性能最好。

2 基于改进的人工蜂群算法的支持向量机参数优化模型

2.1 人工蜂群算法

ABC算法寻找最优解的过程是通过模拟自然界的蜜蜂采蜜过程实现的，算法将蜜蜂分成三种类型：采蜜蜂、观察蜂、侦查蜂，它们根据不同的分工完成不同的任务[11]。采蜜蜂和观察蜂各占整个蜂群的一半，每个食物源只允许对应一个采蜜蜂采蜜，当食物源的花蜜被采完时，则其对应的采蜜蜂转换为侦查蜂。侦查蜂通过观察各个食物源的情况重新选择新的食物源，重复此过程，直到找到最优的食物源。

在该算法中，食物源的优劣与其花蜜量和距蜂巢的距离大小等因素有关，食物源所在的位置就代表优化问题的一个可能解，拥有的花蜜量对应着每个解的适应度。执行ABC算法，首先要进行初始化，随机产生SN个初始解，即采蜜蜂和食物源的数量，每一个解都是一个D维向量，D表示需要优化的参数个数，采用下式均匀的产生初始食物源：

xij=xjmin+rand(0,1)(xjmax-xjmin)i=1,2,…,SNj=1,2,…,D

(5)

初始化之后，就要开始进行对食物源(解)的寻优，人工蜂群算法寻优的过程概括起来由以下三个阶段组成：采蜜蜂阶段、观察蜂阶段、侦查蜂阶段[12]。

采蜜蜂阶段：采蜜蜂对食物源进行开采，对其所在的食物源xij(原始解)附近产生一定的扰动，从而产生候选食物源位置(候选解)，产生过程由下式确定：

vij=xij+φij(xij-xkj)k∈{1,2,…,SN}j∈{1,2,…,D}k≠i

(6)

其中，xi表示搜索空间中第i个食物源，在其附近随机选取一个食物源(候选解)xk，j表示分量，φij为[-1,1]范围内的随机数。从式(6)可以看出，当xij与xkj的差值减小，即两个食物源的距离减小，对当前食物源的扰动减小，蜜蜂的搜索步长就相应的减小，直到收敛于最优解。

观察蜂阶段：对由式(6)产生的各个食物源的候选解进行评估，评估每个新的食物源的花蜜量，即计算解的适应度。从而根据适应度计算出观察蜂选择每个食物源的概率Pi，公式如下：

糖尿病对患者的身体以及心理的影响是十分巨大的[1]。本次研究为了分析研究在老年糖尿病患者中，实施心理护理干预对患者的焦虑抑郁情绪的影响，特选取我院80例患者进行研究，报道如下。

(7)

其中，fitnessi为第i个食物源的适应度，Pi越大，就代表此食物源花蜜量越多，能吸引更多的观察蜂去采蜜。

侦查蜂阶段，对食物源xi进行多次循环开采，当对该食物源的开采次数超过事先设定好的阈值limit，仍然得不到改进，则其对应的解就要被抛弃，采蜜峰变为侦查蜂，重新开始寻找食物源。

2.2 基于交叉突变的ABC算法CMABC

基本的ABC算法在寻优的过程中每次只能选取一个食物源，并且在更新时只能在其中一个方向上进行，这明显限制了算法的优化性能。为了提高ABC算法的整体寻优能力，本文借鉴差分进化算法的交叉突变及选择算子增强算法寻优能力和应用范围的思想[13-14]，将交叉突变算子引入到ABC算法中。

CMABC算法与ABC算法相似，首先进行初始化，设置参数，并对所有的食物源按照十进制编码方式进行编码。然后执行采蜜峰阶段、观察蜂阶段，之后根据以下步骤引入交叉突变算子对种群进行划分，进一步寻找最优解。

1) 根据预先设定的种群划分参数M，对整个种群进行划分，适应度值高的划分为杰出种群P，其余的相对较低适应度值的个体组成子种群Q。

(8)

(9)

最后的侦查蜂阶段，舍弃没有开采价值的食物源，继续寻找新的食物源。

ABC算法中引入交叉算子，通过父代种群P个体与适应度较差的种群Q中个体进行交叉，可以解决在优化多峰问题时出现的算法过早停滞的问题。在种群Q中引入适应度较优的种群P中的个体进行交叉，可以扩大种群的多样性，改进了ABC算法对单峰优化函数收敛过慢的问题。

2.3 基于CMABC算法的SVM入侵检测参数选择

SVM算法的参数选择需要在较大范围内进行，优化过程中很容易陷入局部最优，CMABC算法引入交叉突变算子，将父代种群与适应度较差的种群进行交叉，能有效地解决这个问题。本文采用CMABC算法对SVM的两个重要参数，惩罚因子C和核参数g进行优化。

步骤一 首先对相关参数进行设置，食物源即采蜜蜂的数量SN，食物源最大循环次数limit，终止循环次数Nmc。设定C和g的搜索范围，提高搜索效率。

步骤二 采用实数对参数SVM的参数C和g进行编码，每个解的编码由一个实数向量组成，它与C和g是一种可能的优化个体。在编码空间中，随机生成一个具有SN个个体的初始群体。

步骤三 根据SVM的特性设定适应度函数，优化SVM并应用于入侵检测中的最终目的是提高分类的准确率。适应度函数为：

V=Vacc

(10)

其中，Vacc为SVM的分类准确率。

步骤四 执行采蜜蜂、观察蜂阶段。

步骤五 根据适应度值和预先设定的种群大小进行种群划分，适应度值较高的划分为杰出种群P，其余的为种群Q。P和Q种群中的食物源根据式(8)、式(9)进行突变运算，若vi的适应度值优于xi，则用vi更新xi。

步骤六 侦查蜂阶段，淘汰掉无价值的食物源并随机生成新的食物源。

步骤七 根据选出来的最优食物源的位置，即最优解(C,g)，依据SVM算法对入侵检测数据进行分类，得到较高的分类正确率，有效地提高入侵检测的性能。

3 仿真实验及分析

本文用四个标准测试函数[15]来评估算法CMABC算法的优化性能，并与ABC算法、GABC算法和PSO算法进行对比。

PSO算法中，实体被抽象为粒子，粒子的位置为所求问题的解，根据粒子本身历史最优位置和整个种群的全优位置，在一定的随机扰动下决定每一步的移动方向。在众多的历史位置中记忆并搜索最优解导致早熟收敛，易陷入局部最优，存在进化后期收敛速度慢、精度差等问题。ABC算法是基于蜂群智能搜索行为的优化算法，结合了全局搜索和局部搜索的方法，在函数优化方面优于PSO算法。但ABC算法在模拟蜜蜂采蜜的过程并没有考虑在寻优过程中各种解的特点，与其他进化算法相似，也存在一定的“早熟现象”。

GABC算法的思想是在当前最优值的引导下进行寻优，理论上可以加快单峰函数的收敛速度，但对多峰函数而言，最优值有可能是局部最优的，这就限制了寻优过程。CMABC算法引入种群划分，利用与杰出种群的划分对单峰函数进行优化，提高快速发现最优解的能力，提高了收敛速度；对多峰函数，通过引入交叉算子使已经陷入局部最优的个体脱离局部束缚，提高种群优化能力。

通过两部分实验来对几种算法进行对比分析，第一部分证明了CMABC算法的有效性；第二部分将CMABC算法用于基于SVM的入侵检测参数优化中，并利用入侵检测常用的评价指标对CMABC-SVM进行性能评估。

实验平台选用CPU2.1 GHz，2 GB内存，Windows 7操作系统，采用Java语言结合Libsvm 3.18软件包和Weka软件进行测试分析。Libsvm是台湾大学林智仁副教授等人开发设计的支持向量机软件，Weka为一个公开的数据挖掘工作平台。

3.1 CMABC算法性能分析

四个标准测试函数如下：

(1) Sphere单峰函数

(11)

(2) Rosenbrock单峰函数

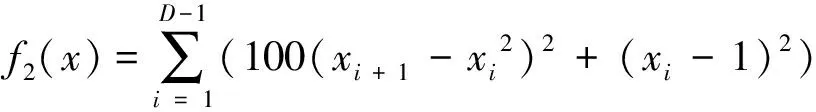
(12)

(3)Rastrigin多峰函数

(13)

(4)Griewank多峰函数

(14)

实验中种群参数M设为0.5，种群大小为80，limit=FoodNumber×D，最大迭代次数Nmc=2000，性能评价分为两部分：(1)固定维度和迭代次数，评估算法的收敛精度；(2)评估算法达到收敛精度的迭代次数。

3.1.1 固定迭代次数的收敛精度

实验独立运行30次后取平均最优值和标准偏差，理想结果值为0。候选解的维数D为20维和40维时的实验结果如表 1和表 2所示。

表1 20维优化测试结果

续表1

表2 40维优化测试结果

可以看出改进的CMABC算法在优化性能上优于ABC算法、GABC算法和PSO算法。只有Rosenbrock函数在20维和40维的时候效果不是很好，经过多次观察该函数在维数较小的时候收敛效果较好，在D=2时，最终收敛到1e-5。当维数增加，搜索范围随之扩大，多峰函数会出现较多的局部极值点，算法对多峰函数的优化效果更好。

3.1.2 固定迭代次数的收速度

设定种群大小和循环次数都不变，在D=20维时ABC算法、CMABC算法、GABC算法和PSO算法的收敛趋势如图1-图3所示。

图1 Sphere函数平均最优值曲线

图2 Griewank函数平均最优值曲线

图3 Rastrigin函数平均最优值曲线

从图1-图3中可以看出，CMABC算法收敛速度上明显优于ABC算法、GABC算法和PSO算法。ABC算法与PSO算法相比也有较明显的优势，实验验证了前面对几种算法所做的理论分析对比CMABC算法优化后，Sphere函数和Griewank函数最终趋于1e-16，对Rastrigin函数CMABC算法在迭代次数800次后收敛到0。GABC算法在迭代次数1000时收敛于0，而ABC算法和PSO算法分别在1600和1800次迭代后收敛于0。CMABC算法通过对父代种群和剩余种群之间的交叉，增强了种群的多样性，有效地提高了算法的收敛速度。

3.2 CMABC算法在入侵检测中的应用

实验采用入侵检测的标准数据集NSL-KDD，数据集包含训练集和测试集，分为正常数据和入侵数据，首先对数据进行标准化预处理并按照各类型数据的比例从中选取一部分数据来进行实验，实验数据类型分布如表 3所示。

表3 实验样本集构成

本文将数据集分成5组进行实验：第一组，正常数据和所有异常数据；第二组，正常数据和Dos类；第三组，正常数据和Probe类；第四组，正常数据和R2L类；第五组正常数据和U2R类。

目前国内外关于入侵检测技术的评价标准，主要有这样几个指标：检测率、误报率、检测精度等[16]，它们的定义分别如下：

检测率TP(True Positive rate)=被发现的攻击样本数/攻击样本的总数

误报率FP(False Positive rate)=被误判的正确样本数/正确样本的总数

检测精度(Precision)=被正确分类的数据样本数/总的样本数

分别将ABC、CMABC、GABC、PSO算法应用于基于SVM的入侵检测中，经过多次对比实验，最终将种群大小SN的值设为20，limit设为50，终止循环次数Nmc为100，这里需要优化SVM的两个参数，所以D为2，将参数的搜索范围定为[0.01,1000]。并在相同条件下，采用相同的数据集将ABC算法、CMABC算法、GABC算法和PSO算法进行优化对比，得到的实验结果如表 4所示。

表4 各组数据集的检测性能

从表4可以看出，通过ABC-SVM算法和CMABC-SVM算法优化SVM参数，对五组数据进行对比，可以看出CMABC算法比其他的几种算法相比都表现出来较好的性能，只有第五组数据由于样本数据较少误报率较高。CMABC-SVM算法在种群的个体之间引入交叉突变算子，平衡了种群的局部开采和全局搜索的能力，使可能已陷入局部最优的个体脱离束缚，跳出局部最优解，通过优化SVM两个重要的参数，提高了基于SVM的入侵检测器的分类性能。

基于SVM入侵检测的实验也验证了3.1节CMABC算法和其他几种优化算法的性能对比实验结果。说明CMABC算法具有实际应用价值，CMABC-SVM算法也进一步提高了入侵检测模型的性能。

4 结 语

基于SVM参数对SVM入侵检测性能的重要性，克服传统优化算法的缺点，本文改进ABC算法，并通过四个标准测试函数验证了CMABC算法的优化有效性。在此基础上本文提出基于CMABC算法的SVM的入侵检测，对SVM的参数惩罚因子C和核参数g进行优化。采用NSL-KDD数据集进行仿真实验，实验表明，CMABC-SVM算法克服了局部最优值的缺陷，使检测器获得更高的检测率、检测精度，较低的误报率，使入侵检测系统可以更好地防御网络入侵。

[1] 苗碧舟．基于数据融合技术的网络异常检测模型的研究[D]．合肥：合肥工业大学, 2013．

[2] Mao Y, Zhou X, Pi D, et al．Parameters selection in gene selection using Gaussian kernel support vector machines by genetic algorithm[J]．Journal of Zhejiang University SCIENCE, 2005, 6B(10):961-973.

[3] 田翔．支持向量机参数选择及训练算法研究[D]．广州：华南理工大学, 2006．

[4] Karaboga D．An idea based on Honey Bee Swarm for numerical optimization[R]．Technical Report-TR06, Erciyes University, 2005.

[5] 刘俊芳，张雪英，宁爱平．PSO和ABC的混合优化算法[J]．计算机工程与应用, 2011, 47(35): 32-34,44．

[6] Zhu G, Kwong S．Gbest-guided artificial bee colony algorithm for numerical function optimization[J]．Applied Mathematics and Computation, 2010, 217(7): 3166-3173.

[7] Unler A, Murat A, Chinnam R B．mr2 PSO: a maximum relevance minimum redundancy feature selection method based on swarm intelligence for support vector machine classification[J]．Information Sciences, 2011, 181(20): 4625-4641.

[8] Engelbrecht A P．Particle swarm optimization[C]//Proceedings of the Companion Publication of the 2015 on Genetic and Evolutionary Computation Conference. ACM, 2015: 65-91.

[9] 马蕾，汪西莉．基于支持向量机协同训练的半监督回归[J]．计算机工程与应用, 2011, 47(3): 177-180．

[10] 刘鲭洁，陈桂明，刘小方，等．基于遗传算法的SVM参数组合优化[J]．计算机应用与软件,2012,29(4):94-96,100．

[11] 张新明，李晓安，何文涛，等．基于排名映射概率的混沌人工蜂群算法[J]．计算机科学, 2013, 40(12): 98-103．

[12] 邱剑锋．人工蜂群算法的改进方法与收敛性理论的研究[D]．合肥：安徽大学, 2014．

[13] Qin A K, Suganthan P N. Self-adaptive differential evolution algorithm for numerical optimization[C]//Proceedings of the 2005 IEEE Congress on Evolutionary Computation, 2005:1785-1791.

[14] Tinoco J C V, Coello C A C．hypDE: A hyper-heuristic based on differential evolution for solving constrained optimization problems[M]．EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation II．Berlin: Springer，2013: 267-282．

[15] 纪震，廖惠连，吴青华．粒子群算法及应用[M]．北京：科学出版社, 2009：72-79．

[16] 贾伟峰．网络入侵检测中机器学习方法的应用研究[D]．成都：电子科技大学, 2009．

APPLICATION OF IMPROVED SUPPORT VECTOR MACHINE ALGORITHM OPTIMIZED BY ARTIFICIAL BEE COLONY ALGORITHM IN INTRUSION DETECTION

Liu Ming1Huang Fanling2Fu Yanming3Yang Xiaoling3

1(CollegeofComputerScienceandInformationEngineering,AnyangInstituteofTechnology,Anyang455000,Henan,China)2(SchoolofSoftware,TsinghuaUniversity,Beijing100084,China)3(SchoolofComputer,ElectronicsandInformation,GuangxiUniversity,Nanning530004,Guangxi,China)

Aiming at the problem that the traditional parameters optimization algorithm may fall into locally optimal solution, a optimization method of parameter of Support Vector Machine(SVM) which applied Crossover Mutation Artificial Bee Colony(CMABC) is proposed to solve this problem and applied to intrusion detection, which is based on Artificial Bee Colony(ABC) algorithm. By introducing Crossover Mutation operator to improve ABC algorithm and dividing bee colony according to different fitness value, the locally optimal solution is effectively avoided and the convergence speed is improved. The standard test function is used to verify the effectiveness of the algorithm, what’s more, the performance of the proposed algorithm is simulated by adopting NSL-KDD datasets of intrusion detection. Finally, the experimental results show that the proposed method is an efficient way to improve the classification performance of intrusion detection.

Intrusion detection Support vector machine Artificial bee colony Crossover mutation

2015-07-01。国家自然科学基金项目(61262072)；广西大学博士基金项目(DD060074)。刘铭，硕士生，主研领域：入侵检测，信息安全。黄凡玲，硕士生。傅彦铭，副教授。杨晓玲，硕士生。

TP309

A

10.3969/j.issn.1000-386x.2017.01.042