基于Wright-Fisher过程的WSNs节点信任随机演化策略
2017-03-01曹奇英许洪云沈士根
王 丁 曹奇英* 许洪云 沈士根
1(东华大学计算机科学与技术学院 上海 201620) 2(东华大学信息科学与技术学院 上海 201620)3(绍兴文理学院计算机科学与工程系 浙江 绍兴 312000)4(嘉兴学院数理与信息工程学院 浙江 嘉兴 314001)
基于Wright-Fisher过程的WSNs节点信任随机演化策略
王 丁1曹奇英1*许洪云2沈士根3,4
1(东华大学计算机科学与技术学院 上海 201620)2(东华大学信息科学与技术学院 上海 201620)3(绍兴文理学院计算机科学与工程系 浙江 绍兴 312000)4(嘉兴学院数理与信息工程学院 浙江 嘉兴 314001)
为解决无线传感器网络节点间的信任影响节点协作的问题,考虑到节点数量有限及个体随机性,基于Wright-Fisher过程的随机演化博弈,提出WSNs节点信任随机演化策略,并加入与节点信任相关的惩罚机制。该策略弥补了复制子动态不适用于节点数量有限的WSNs节点信任演化建模问题,经过随机动力学分析,推导并证明了达到演化稳定状态的定理。最后通过实验验证定理并分析惩罚力度和选择强度对演化稳定状态的影响。
无线传感器网络 信任 Wright-Fisher过程 随机演化博弈 惩罚机制
0 引 言
无线传感器网络WSNs[1]是由数量众多的传感器节点以自组织和多跳等方式组成的无线网络。WSNs中源节点采集的数据需要被多个节点连续转发后才能到达目标节点。如果一个节点信任其他节点,那么它会帮助其他节点转发数据包并提高自身的信誉度,也就是获得了收益。但在转发数据包的同时,节点本身需要付出一定的成本,如消耗能量、自身任务延时传输等。由于获得收益和付出成本是一个矛盾,因此若存在较多节点不信任其他节点的情况,就会导致WSNs节点无法正常协作。因此,节点之间信任与否会直接影响到WSNs的节点协作和整个网络的安全。
近几年来,已有许多学者使用演化博弈论的方法来分析网络中的一些矛盾问题。文献[2]分析了无限总体演化博弈的演化稳定策略,并与复杂网络博弈的演化稳定策略进行了比较,提出了一种适用于网络演化博弈的演化稳定策略新定义;文献[3]将演化博弈应用于延迟容忍网络的非合作转发控制方面,并分析了交互次数对演化均衡的影响。在WSNs研究领域,文献[4]提出了一种基于演化博弈的资源控制协议,用于缓解WSNs内资源竞争矛盾。文献[5]将演化博弈与WSNs节点信任决策结合,建立了WSNs节点信任博弈模型,提出并证明了在不同的参数条件下达到演化稳定策略的定理。文献[6]和文献[7]在文献[5]的基础上分别引入了节点的反思机制和模仿机制,并考虑了网络不可靠因素对模型的影响。
上述文献所用的演化博弈模型大都是针对无限总体的对象模型,而实际情况中的研究对象一般都是有限总体。针对这个问题,学者们将随机过程应用到演化博弈,形成了以有限总体为研究对象的随机演化博弈。文献[8]研究了服务提供商面对软硬件服务攻击时的安全和可信机制,提出了一种适用于虚拟传感器服务的安全、可信的随机演化联合博弈防御框架。文献[9]针对网构软件中存在的服务问题,将网构软件的服务差异化,并把基于Wright-Fisher过程的两策略博弈拓展到多策略,提出了一种博弈参与者具有多个策略的信任演化博弈模型。文献[10]针对网构软件的服务质量QoS问题,在文献[9]的基础上考虑了白噪声对博弈模型的影响,构建了带有白噪声的多策略Wright-Fisher过程信任演化博弈模型。文献[11]把Moran过程应用到无线网络的接入选择中,并从多策略的角度改进了局部更新机制。文献[12]综述并总结了随机演化博弈模型与网络群体行为在理论分析与建模应用等方面的研究。随机演化博弈虽然在其他领域已有较广的应用,但是目前在WSNs中应用还较少。
本文使用基于两策略、频率相关的Wright-Fisher过程的随机演化博弈模型来分析无线传感器网络中存在的节点信任问题。数量有限的WSNs节点在选择信任与否时体现出了重复性、有限理性等特征,而对于整个WSNs来说,其目标是在达到总体收益较高状态的同时也能够保持足够的稳健性,这些特征恰好满足随机演化博弈的要求。据此,本文建立了WSNs节点信任演化策略,使节点在无外界干预的情况下动态演化,各个节点根据Wright-Fisher机制自行调整下一次博弈的策略,使WSNs逐渐演化到稳定状态。在到达演化稳定状态之后,WSNs中的绝大部分节点将会选择信任策略并保持不变。在信任演化[5]的基础上,通过考虑WSNs中有限节点数量的情况,引入惩罚机制来构造信任博弈模型,并利用Wright-Fisher过程来分析节点信任演化动态,使WSNs节点信任策略更趋近真实状况,并得出到达演化稳定状态的定理,分析影响到达演化稳定状态的影响因子。
1 基于Wright-Fisher过程的随机演化博弈模型
博弈论是分析博弈个体在进行博弈时表现出的行为并研究博弈个体的博弈最优策略的理论。一个标准的博弈由3个要素组成:博弈个体、策略集合和收益函数[13]。博弈个体是参与博弈的主观个体,每个博弈个体分别从策略集合中选取一种策略与另一个博弈个体进行博弈,收益函数是博弈个体依据其策略与对手博弈所获得的收益。收益函数可由收益矩阵的形式给出。经典博弈的博弈个体总是完全理性[13]的,也就是说,博弈个体总是选择收益最大的策略与对手进行博弈。
演化博弈论在经典博弈的基础之上,结合博弈分析理论和生物种群的演化过程,形成了一个新的博弈论分支。在演化博弈论中,博弈个体都是有限理性[14]的,它把所有博弈个体的总体视为一个种群,将种群作为基本的研究对象,研究博弈个体在多次动态博弈中的策略演化状况。演化博弈有两个核心概念:演化稳定策略ESS(Evolutionary Stable Strategy)和复制子动态RD(Replicator Dynamic)。演化稳定策略反映了博弈均衡解的稳定性状态,复制子动态则描述了博弈过程向演化稳定状态收敛的变化动态。复制子动态可以由式(1)表示:
(1)
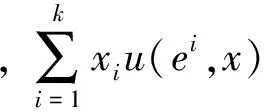
经典的演化博弈的研究对象一般是无限总体,因此使用微分形式的复制子动态方程能够较好地反映研究对象的动态演化过程。但在实际情况中,研究对象都是总体数量有限的,并且个体的随机性在有限总体的博弈过程中起着非常重要的作用。因此基于随机过程的随机演化博弈成为了研究有限总体演化博弈的重要途径,其中较重要的3种模型是Moran过程[15]、Wright-Fisher过程[16]和随机配对过程[17]。其中Wright-Fisher过程由于能够在一次迭代内进行同步更新,相较于只能异步更新的其他两种过程更具现实意义。
在Wright-Fisher过程中,总体中的每个个体在进行策略更新时,会依据策略的适应性强弱不同分别选择适合自身的策略。之后每个个体都会产生多个与自身选择的策略相同的后代个体,得到一个总数大于总体数量的后代集合,再从这个集合中随机选出等于总体数量的新个体取代当前个体。Wright-Fisher过程可描述如下[16]:
假设在一个总体中,个体数量为N,策略集合为{S1,S2},每个个体之间进行两人两策略对称性博弈,收益矩阵如式(2)所示:
(2)
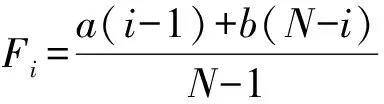
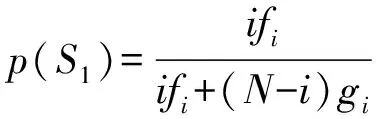
(3)
2 WSNs节点信任演化策略
2.1 博弈模型
基于文献[5]的研究,本文在WSNs节点信任博弈时加入了与节点信任相关的惩罚机制。在WSNs中,节点可以与邻居节点进行主动式的交互,选择信任策略与对方协作,或选择不信任策略不与对方协作。在本文中并不涉及节点信任度的计算或量化过程,而是在节点选择不信任策略时给予一定的惩罚。
记GT表示当前节点信任交互的对方节点而成功帮助对方转发数据包带来的收益;GC表示因对方节点信任当前节点,帮助转发了当前节点的数据包,当前节点所获得的收益;GD表示当前节点因选择不信任策略,不帮助对方转发数据包,节省了能量,从而延长了节点的生存周期所获得的收益;C表示当前节点向对方节点发送自身的数据包或帮助转发对方节点的数据包所产生的传输成本;L表示当前节点所发送的源数据包未能成功到达目的地而造成的损耗;β表示当前节点因选择了不信任策略而受到的惩罚损耗。
下面对各种可能发生的交互状态分别进行讨论:
(1) 两个节点在进行交互时均选择了信任策略
此时双方节点均会转发对方的数据包并向对方发送自身的数据包,获得收益GT+GC,并消耗了发送两次数据包的成本2C,因此双方节点的收益均为:GT+GC-2C。
(2) 两个节点在进行交互时有一个节点选择了信任策略,而另一个节点选择了不信任策略
此时选择了信任策略的节点会帮助对方节点转发数据包,从而获得收益GT,同时消耗了转发成本C,但由于对方节点选择了不信任策略而导致自身的数据包无法被对方成功转发,会造成L的损失,因此选择信任策略的节点收益为GT-C-L。选择不信任策略的节点会向选择信任策略的节点发送数据包并被成功转发而获得收益GC,消耗了成本C。又因它不会转发对方的数据包节省了能量从而延长了自身的生存周期,获得收益GD,但由于它选择了不信任策略而受到惩罚损失了β,因此选择了不信任策略的节点收益为:GC+GD-C-β。
(3) 两个节点在进行交互时均选择了不信任策略
由于两个节点都不信任对方节点,因此节点之间不会向对方节点发送数据包或转发对方数据包,两个节点都节省能量获得收益GD,但受到选择不信任策略的惩罚从而均损失了β,因此两个节点的收益均为:GD-β。
定义1 WSNs节点信任博弈是一个由四元组(P,N,S,F)表示的对称博弈。其中参与者P为WSNs中所有节点的集合;N为参与者的总体数量;策略集合为S={S1,S2},S1为信任策略,S2为不信任策略;F为WSNs节点在一次两人两策略对称博弈时的收益函数,如表1所示。

表1 一次博弈收益矩阵
2.2 引入Wright-Fisher过程
在经典的演化博弈中,演化稳定策略和复制子动态方程都是基于博弈个体的数量是无限多且不同策略的个体均匀分布的假设。但对于参与者数量有限的博弈,整个系统的状态将成为离散点的集合,因此微分方程将不再适用于离散状态的随机演化博弈。
由于WSNs的节点数量是有限的,进行博弈的节点可以看作出自一个种群的有限总体,因此在WSNs节点信任博弈中引入Wright-Fisher过程,该模型能满足WSNs节点信任博弈的总体有限性、离散性和随机性等特征。
假设在WSNs节点信任博弈中,节点的总数为N,有i个节点选择信任策略,则有N-i个节点选择不信任策略。在进行节点信任博弈时,需剔除自己和自己博弈的情况,因此可得:任一节点选择信任策略的期望收益为:
任一节点选择不信任策略的期望收益为:
假设在演化博弈中,收益函数对该策略适应度的影响因子为ω,ω∈[0,1],则在WSNs节点信任博弈中,信任策略的适应度为:
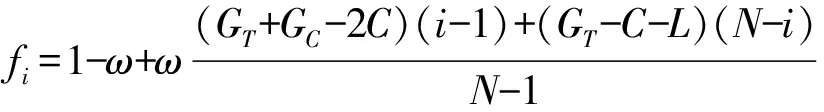
由于适应度要求收益函数为非负数,因此对策略的收益函数还应加以修正,使其满足适应度的条件。
在无限总体的确定性复制子模型和Fudenberg及Harris的随机复制子模型[18]中,总体的动态演化过程是由每个策略的适应度和平均适应度之差决定的。因此对这些模型来说,只要ω>0,参数ω只会影响演化的速度而不会影响长期的策略选择。而对于有限总体来说,参数ω却会影响长期的策略选择。当0<ω≤1时,策略的收益对适应度的影响较小,因此节点在选择策略时策略的收益对选择影响较小,称为弱选择;当ω=0时,节点在选择策略时完全不考虑收益,此时节点完全随机选择策略,称为中性选择;当ω=1时,节点在选择策略时只考虑收益,对应于经典博弈的完全理性,称为强选择,也称完全选择。选择强度ω的引入,使得Wright-Fisher过程具有了有限理性的特性。
定义2 在不考虑自身博弈情况的WSNs节点信任博弈中,信任策略的适应度为fi=1-ω+ωFi,不信任策略的适应度为gi=1-ω+ωGi,其中i为选择信任策略的节点数量,Fi为WSNs节点在博弈时选择信任策略的收益且:
Gi为WSNs节点在博弈时选择不信任策略的收益且:
ω∈[0,1]为收益对适应度的选择强度,z为常数使得收益函数为非负数。
WSNs的节点在进行下一次博弈之前,会进行以下步骤更新策略:
1) 每个节点都会生成相同数量的多个选择相同策略的后代,这些后代完全继承父代节点选择的策略,构成一个数量为N的整数倍个后代的集合;
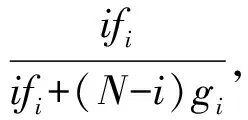
3) 新一代后代完全替换上一代,完成节点的一代更新。
记X(n)为选择信任策略的节点在第n代时的数量,则X(n)是一个状态空间为{0,1,…,N}的马尔可夫链,其中状态{1,…,N-1}为转移态,状态0和状态N为吸收态。对于任意初始状态的WSNs节点,在经过有限次博弈后,一定会达到某一吸收态并不再改变博弈策略。
定义3 WSNs节点信任博弈中,在一次博弈后的策略更新时,选择信任策略的节点数量从i变化到j的概率为:
(4)
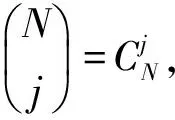
2.3 随机动力学分析
由于Wright-Fisher过程是在总体数量有限情况下的随机过程,因此在N较大时,假设t时刻时选择信任策略的节点在总体的比例为x,x∈[0,1],又因演化博弈的更新时间步长为Δt,所以可通过Langevin方程[19]来近似代替表示x关于时间t的变化率,有:
(5)

由定义1-定义3有:
(6)
(7)
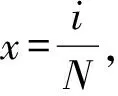
(8)
v(x)→0
(9)
其中f=1-ω+ω[x(z+GT+GC-2C)+(1-x)(z+GT-C-L)],g=1-ω+ω[x(z+GC+GD-C-β)+(1-x)(z+GD-β)]。
将式(6)和式(7)代入式(5)可得选择信任策略节点比例的动态方程:
(10)
其中f=1-ω+ω[x(z+GT+GC-2C)+(1-x)(z+GT-C-L)],g=1-ω+ω[x(z+GC+GD-C-β)+(1-x)(z+GD-β)]。
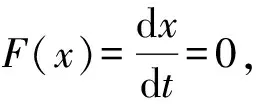
演化博弈的演化稳定状态x*具有稳定性,能够对微小的扰动具有健壮性,这个性质对应于微分方程的稳定性定理,因此以上两个解还需满足F′(x)<0才能成为演化稳定状态。

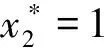
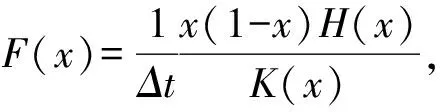
F′(x)= {[(1-x)H(x)-xH(x)+x(1-x)H′(x)]K(x)-
x(1-x)H(x)K′(x)}/[Δt·K2(x)]
将F(x)=0的两个解代入可得:
=(GD-GT+C+β)/(1-ω+ω(z+GT+GC-2C))
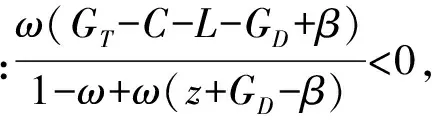
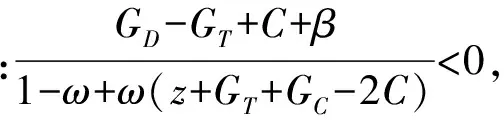
定理1表明:WSNs中的节点在进行信任博弈时,若满足定理1的条件,那么对于两个进行博弈的节点来说,选择不信任策略的收益总是大于选择信任策略的收益,因此节点在进行下一次博弈的策略更新时,均会更趋向于选择不信任策略。也就是说,不信任策略是严格占优且演化稳定的,无论WSNs的节点选择两个策略的初始比例如何,经过一定次数的博弈,绝大部分节点最终都会选择不信任策略且保持不变。
定理2表明:WSNs中的节点在进行信任博弈时,若满足定理2的条件,那么对于两个进行博弈的节点来说,选择信任策略的收益总是大于选择不信任策略的收益,因此节点在进行下一次博弈的策略更新时,均会更趋向于选择信任策略。也就是说,信任策略是严格占优且演化稳定的,无论WSNs的节点选择两个策略的初始比例如何,经过一定次数的博弈,绝大部分节点最终都会选择信任策略且保持不变。
由定理1和定理2可知,要使整个WSNs网络具有良好的稳定性和节点协作性,需促使WSNs的节点在信任博弈时选择信任策略,因此在设计WSNs信任机制时应使其尽量符合定理2的条件。惩罚因子β的引入会使WSNs节点在选择不信任策略时受到一定的惩罚,产生更多的损失。当β逐渐增大,惩罚力度也逐渐变大时,会使WSNs逐渐满足定理2的条件,而逐渐偏离定理1的条件。当β增大到一定程度,使得WSNs节点信任博弈不满足定理1,但是满足定理2的条件时,WSNs将处于比较理想的稳定状态,此时网络内的所有节点在经过有限次博弈之后都会最终选择信任策略。
3 实验分析
3.1 定理验证实验
本文的实验环境为Matlab R2012b。实验设定WSNs节点信任博弈中的不同参数,分别满足定理1和定理2的条件,来验证WSNs节点信任博弈中的演化稳定策略。实验共设定两组参数,在第一组中,GT=8,Gc=6,GD=3,C=8,L=4,β=2,z=4,ω=0.9;在第二组中,GT=18,Gc=6,GD=3,C=8,L=4,β=2,z=4,ω=0.9。实验结果如图1所示。
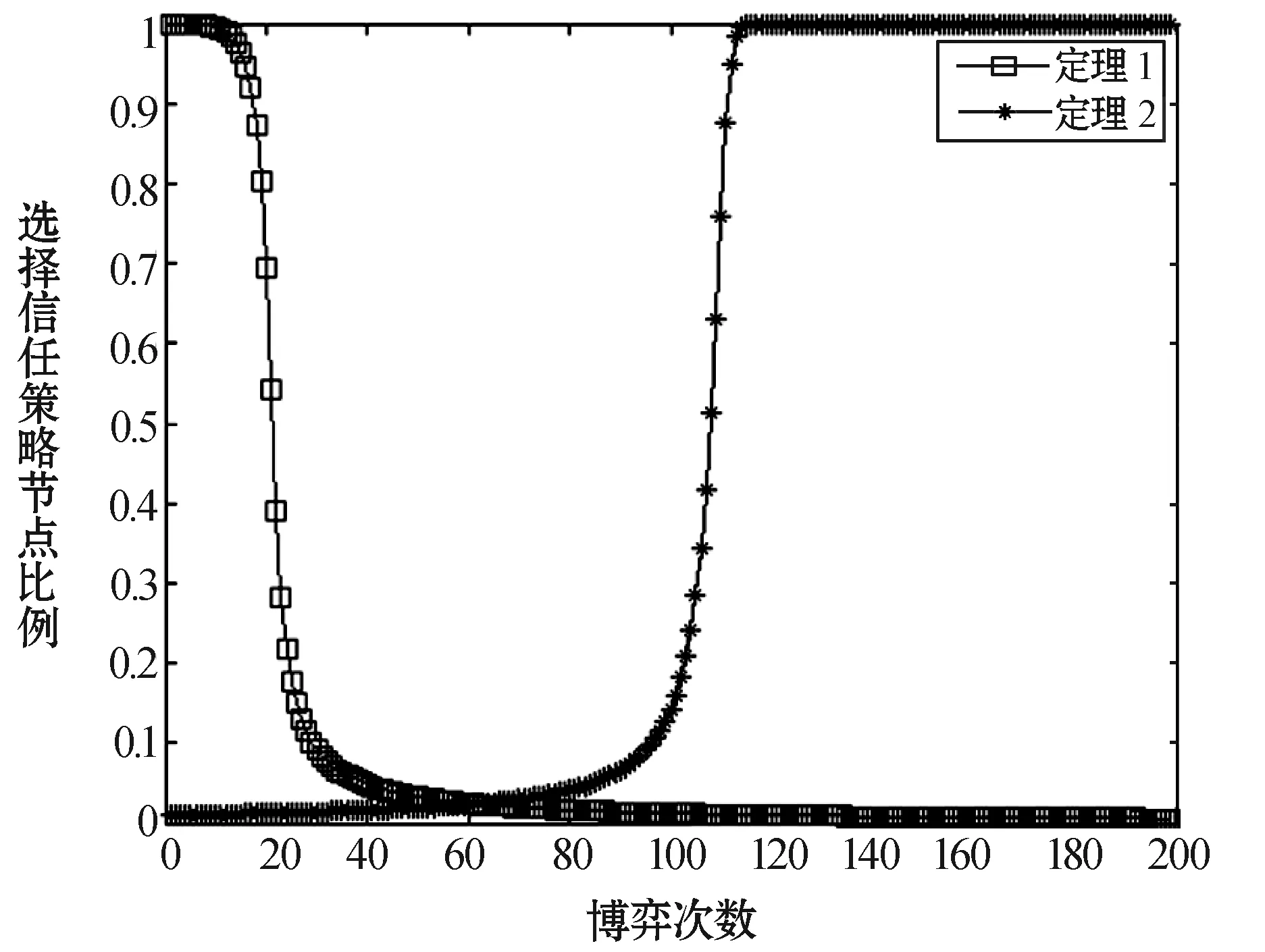
图1 信任演化曲线
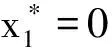
3.2 影响因子验证实验
实验中分别使用不同数值的惩罚因子β和选择强度ω来观察其对WSNs节点信任博弈的影响,并根据实验结果给出优化WSNs节点信任博弈的对策。本实验共设2组,第1组分析惩罚因子β对定理2的影响,第2组分析选择强度ω对定理2的影响。
1) 惩罚因子β的影响
实验设定:GT=18,Gc=6,GD=3,C=8,L=4,z=4,ω=0.9,β分别设定为3和2。两组数据均满足定理2,实验结果如图2所示。
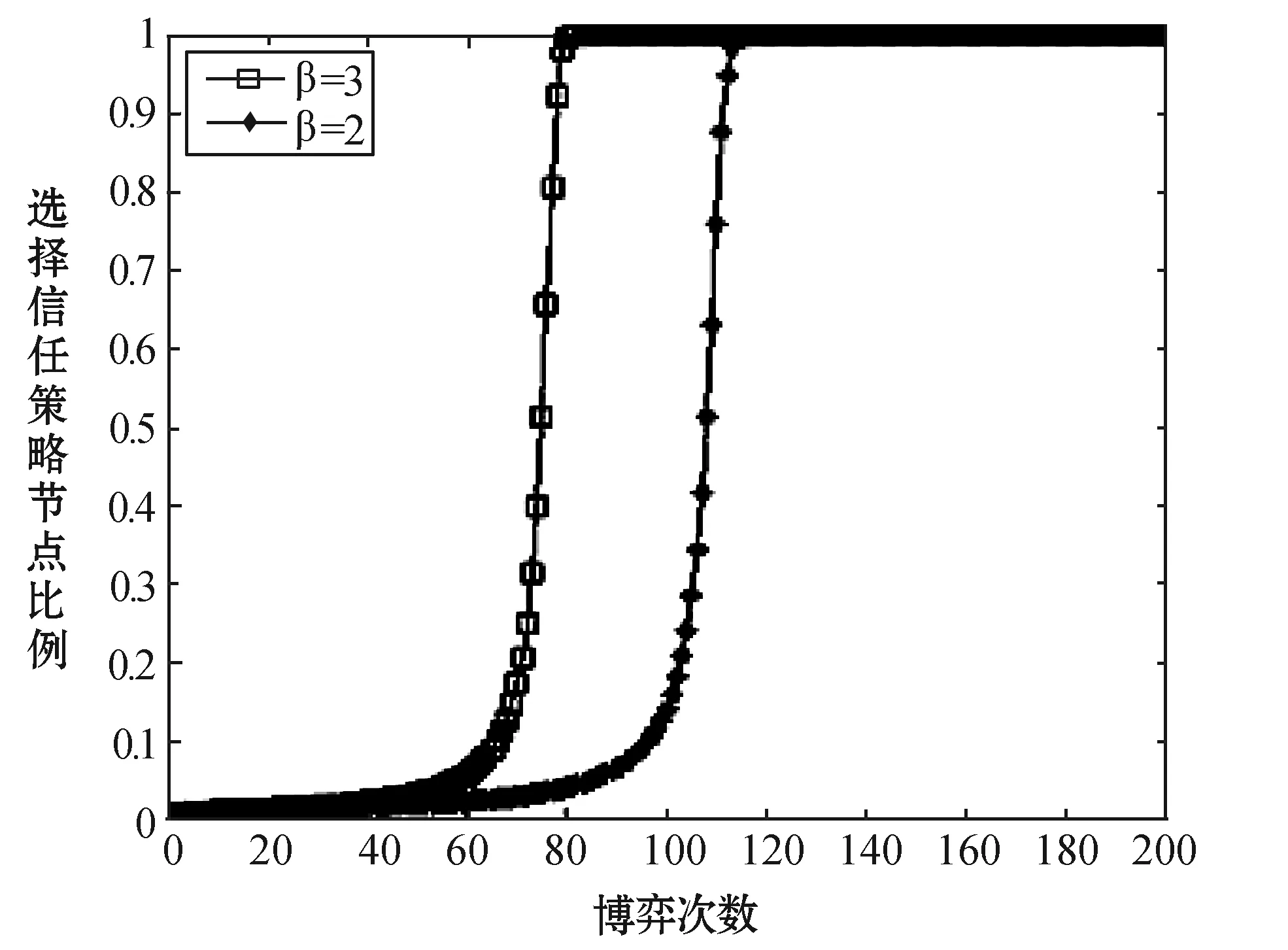
图2 惩罚因子对定理2的影响
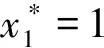
2) 选择强度ω的影响
实验设定:GT=18,Gc=6,GD=3,C=8,L=4,β=2,z=4,ω分别设定为0.4和0.9。两组数据均满足定理2,实验结果如图3所示。

图3 选择强度对定理2的影响
4 结 语
节点间的信任问题是WSNs节点进行相互协作的重要基础,促进WSNs节点互相信任能够促使整个WSNs网络快速、稳健地达到稳定状态。本文根据WSNs中节点数量有限等特点,引入与节点信任相关的惩罚机制,提出了基于Wright-Fisher过程的WSNs节点信任随机演化策略,弥补了复制子动态不适用于节点数量有限的WSNs中的缺陷,使WSNs节点信任博弈策略更符合实际情况。在此基础之上,对随机演化博弈模型进行了动力学分析,得出并证明了WSNs节点信任博弈达到演化稳定状态的定理。经过分析与实验验证了结论:提高节点选择不信任策略的惩罚力度和节点选择信任策略的选择强度均能有效促进WSNs节点的互信程度,实现网络的安全与稳定。本文提出的基于Wright-Fisher过程的WSNs节点信任随机演化策略,为WSNs节点信任和协作问题研究提供了理论依据。
[1] Yick J,Mukherjee B,Ghosal D.Wireless sensor network survey[J].Computer Networks,2008,52(12):2292-2330.
[2] Cheng D,Xu T,Qi H.Evolutionarily Stable Strategy of Networked Evolutionary Games[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(7):1335-1345.
[3] El-Azouzi R,Pellegrini F D,Sidi H B A,et al.Evolutionary forwarding games in delay tolerant networks:Equilibria,mechanism design and stochastic approximation[J].Computer Networks,2013,57(4):1003-1018.
[4] Farzaneh N,Yaghmaee M H.An Adaptive Competitive Resource Control Protocol for Alleviating Congestion in Wireless Sensor Networks:An Evolutionary Game Theory Approach[J].Wireless Personal Communications,2015,82(1):123-142.
[5] 沈士根,马绚,蒋华,等.基于演化博弈论的WSNs信任决策模型与动力学分析[J].控制与决策,2012,27(8):1133-1138.
[6] 李紫川,沈士根,曹奇英.基于反思机制的WSNs节点信任演化模型[J].计算机应用研究,2014,31(5):1528-1531,1535.
[7] Li Y,Xu H,Cao Q,et al.Evolutionary Game-Based Trust Strategy Adjustment among Nodes in Wireless Sensor Networks[J].International Journal of Distributed Sensor Networks,2015,2015:818903.
[8] Liu J,Shen S,Yue G,et al.A stochastic evolutionary coalition game model of secure and dependable virtual service in Sensor-Cloud[J].Applied Soft Computing,2015,30:123-135.
[9] 印桂生,王莹洁,董宇欣,等.网构软件的Wright-Fisher多策略信任演化模型[J].软件学报,2012,23(8):1978-1991.
[10] Yin G,Wang Y,Dong Y,et al.Wright-Fisher multi-strategy trust evolution model with white noise for Internetware[J].Expert Systems with Applications,2013,40(18):7367-7380.
[11] 冯光升,王慧强,周沫,等.基于Moran过程的无线网络接入选择方法[J].北京邮电大学学报,2014,37(4):10-14.
[12] 王元卓,于建业,邱雯,等.网络群体行为的演化博弈模型与分析方法[J].计算机学报,2015,38(2):282-300.
[13] Fudenberg D,Tirole J.博弈论[M].姚洋校,等,译.北京:中国人民大学出版社,2010.
[14] Weibull J W.演化博弈论[M].王永钦,译.上海:上海人民出版社,2006:40-86.
[15] Moran P A P.The Statistical Processes of Evolutionary Theory[M].Oxford:Clarendon Press,1962.
[16] Traulsen A,Claussen J C,Hauert C.Coevolutionary dynamics:from finite to infinite populations[J].Physical Review Letters,2005,95(23):238701.
[17] Traulsen A,Pacheco J M,Nowak M A.Pairwise comparison and selection temperature in evolutionary game dynamics[J].Journal of Theoretical Biology,2007,246(3):522-529.
[18] Fudenberg D,Harris C.Evolutionary dynamics with aggregate shocks[J].Journal of Economic Theory,1992,57(2):420-441.
[19] Ohtsuki H,Pacheco J M,Nowak M A.Evolutionary graph theory:breaking the symmetry between interaction and replacement[J].Journal of Theoretical Biology,2007,246(4):681-694.
STOCHASTIC EVOLUTIONARY TRUST STRATEGY OF WSNS NODES BASED ON WRIGHT-FISHER PROCESS
Wang Ding1Cao Qiying1*Xu Hongyun2Shen Shigen3,4
1(CollegeofComputerScienceandTechnology,DonghuaUniversity,Shanghai201620,China)2(CollegeofInformationScienceandTechnology,DonghuaUniversity,Shanghai201620,China)3(DepartmentofComputerScienceandEngineering,ShaoxingUniversity,Shaoxing312000,Zhejiang,China)4(CollegeofMathematics,PhysicsandInformationEngineering,JiaxingUniversity,Jiaxing314001,Zhejiang,China)
To solve the problem of trust decisions among WSNs nodes which affects the cooperation between nodes,considering limited numbers of nodes and individual stochastic effect,a stochastic evolutionary trust strategy of WSNs nodes based on Wright-Fisher process is proposed,and a punishment mechanism related to the trust level of nodes is also introduced.The strategy remedied the defect that replicator dynamics was inapplicable to the WSNs due to the limited numbers of nodes.Theorems of arriving at the evolutionary stable state were deduced and proved through the analysis of stochastic dynamics.Experiments verified the conclusions and analyzed the impacts of punishment levels and selection intensities.
Wireless sensor networks(WSNs) Trust Wright-Fisher process Stochastic evolutionary game Punishment mechanism
2015-10-28。国家自然科学基金项目(61272034)。王丁,硕士生,主研领域:无线传感器网络,博弈论。曹奇英,教授。许洪云,博士生。沈士根,教授。
TP393
A
10.3969/j.issn.1000-386x.2017.01.020
