模拟发射加速度载荷条件下管状推进剂装药的应变率研究

李 猛 ，赵凤起，徐司雨，裴 庆，郝海霞，姚二岗，姜菡雨

(西安近代化学研究所燃烧与爆炸技术重点实验室，陕西 西安 710065)

模拟发射加速度载荷条件下管状推进剂装药的应变率研究

李 猛 ，赵凤起，徐司雨，裴 庆，郝海霞，姚二岗，姜菡雨

(西安近代化学研究所燃烧与爆炸技术重点实验室，陕西 西安 710065)

采用LS-DYNA软件建立了有限元模型，计算了模拟发射加速度条件下管状推进剂装药的应变及应变率；分析了10000g(g为重力加速度)条件下装药的结构响应，讨论了不同加速度载荷(5000～15000g)、装药结构尺寸对最大等效应变和应变率的影响。结果表明，在装药承受加速度载荷过程中，最大等效应力和应变均发生在底部内孔附近；随着轴向加速度由5000g增加到15000g，等效应变-时间曲线和应变率-时间曲线变化趋势基本相同，最大应变率由13s-1线性增至35s-1，处于中等应变率范围；装药长度由120mm增至200mm时，最大等效应变和应变率分别增加了1.83%和2.63%。

管状推进剂装药；发射加速度；应变率；数值模拟

引 言

炮射弹药的快速发展大大增强了传统火炮的火力范围和射击精度，实现了火炮武器系统的远程、精确打击[1-4]。俄罗斯、美国、以色列、法国等竞相开展了相关研究，如俄罗斯的9M系列、美国的XM982神剑及P44、以色列的Star、法国的鹈鹕等。其主要利用火炮发射获得较高初速度，再通过增程发动机进一步加速，实现远射程打击，主要特点是高初速、高膛压，因此固体推进剂装药在发射过程中要承受很高的加速度载荷，对装药结构完整性产生较严重的影响，由于较大的高膛压冲击压力，装药将产生较大的变形，影响武器系统安全性和可靠性，因此迫切需要提高固体推进剂装药的抗过载能力。

应变率是影响力学性能的重要因素[5-7]。研究表明，随着应变率的变化，材料的屈服强度等将会发生很大变化，进而影响结构的动态响应。国外对发射加速度载荷条件下固体推进剂装药的动态响应研究较为深入[7-9]，使炮射弹药的安全性得到较大提高。国内对发射加速度载荷条件下固体推进剂装药应变率关注较少，主要采用低应变率及与高应变率实验数据联合拟合的材料模型对其力学响应进行研究[11-13]，缺乏中等应变率实验数据拟合参数，使得结构响应可靠性无法得到验证。因此研究高加速度载荷作用下推进剂装药的应变率将有助于针对性地开展抗过载推进剂装药研制及实验评估。

本研究采用有限元方法计算了10000g条件下管状装药的结构响应，获得应变和应变率，进一步对不同加速度载荷(5000～15000g)和不同装药结构对最大等效应变和应变率的影响进行了分析，为开展高加速度条件下装药结构设计和实验提供参考。

1 数值模型

1.1 本构模型

假设固体推进剂为满足热流变简单性假设的各向同性线性黏弹性材料[7-13]，以张量形式描述的应力松弛函数关系式为：

(1)

式中，应力松弛函数通常按Prony级数形式给出：

(2)

式中：σij(t)为应力张量；εij(τ)为应变张量；G(t)为剪切松弛模量；G∞为长期剪切松弛模量；β为松弛衰减系数。

选用某炮射导弹研究报告中使用的材料特性参数[11-12]，固体推进剂密度为1647kg/m3，短时间剪切模量为1.25×108Pa，平衡时剪切模量为6.5×108Pa，体积模量为2×109Pa，松弛时间常数为0.02，泊松比为0.49。发动机壳体采用优质合金钢，材料本构模型简化处理为线弹性材料模型[8-15]。壳体材料的密度为7800kg/m3，杨氏模量为2×1011Pa，泊松比为0.3。

1.2 加载分析

炮射弹药发射时的物理过程：炮射弹药放入自由装填式火炮中，发射药被激发急剧燃烧，产生高温高压气体，气体膨胀作功，使弹体加速向炮口移动，其最终速度是由发射药燃烧形成的高压气体压力持续冲击获得的。固体火箭发动机作为炮射弹药的关键部件，其物理过程和受力特点与弹体类似，装药高加速度是由高膛压加载形成的，本研究采用已有的发射安全性理论，研究整体惯性作用阶段[5]。

假设固体推进剂装药承受轴向加速度载荷为5000g～15000g，各加速度载荷加载曲线对应的时间历程相同。图1为管状装药在炮射导弹发射过程中所承受的加速度-时间曲线，其中载荷上升时间均为4ms，稳定时间均为6ms。

图1 轴向加速度-时间加载曲线Fig.1 Loading curves of axial acceleration vs.time

1.3 有限元模型

选用标准管状推进剂装药，装药外径为45mm，内径为8mm，长为120mm。选用Φ50mm发动机，壳体与装药的间隙为2.5mm。由于装药与壳体结构几何对称，取结构的四分之一进行三维有限元建模，为保证计算精度，采用六面体八节点单元进行网格划分，共生成32025个节点和27600个单元，有限元计算网格如图2所示。

图2 管状装药及壳体有限元网格Fig.2 The finite element mesh of tubular charge and shell

定义炮射弹药向炮口方向为轴向正方向，则装药底部与发动机接触区在轴向负方向被约束，对称面上施加相应的对称约束；壳体外侧面施加固定约束；壳体内侧面与装药外侧面设置接触，忽略装药与壳体之间的摩擦；由于采用的装药是厚壁柱壳，因此内径不受约束，是自由面。

1.4 推进剂装药破坏的经验判据

在发射加速度载荷作用下，推进剂装药内部存在较大的应变，当应变值达到装药的最大应变能力时，其内部会产生裂纹，裂纹进一步扩展将会导致装药断裂。因此，一般采用最大应变理论作为药柱破坏的经验准则，Von Mises应变表达式为：

(3)

但在承受发射加速度等短时瞬态冲击载荷作用时，因装药的瞬时弹性模量较高，力学响应产生的应力水平较高。因此，必要时需采用Von Mises应力作为装药结构完整性评定的判据：

(4)

2 数值计算结果及分析

2.1 管状推进剂装药应变率分析

为了获得管状推进剂装药在10000g加速度条件下的最大应变率，首先计算出装药在加载10ms内的等效Von Mises应变云图，找出最大等效Von Mises应变对应的云图，从最大等效Von Mises应变云图确定最大等效Von Mises应变对应的单元号，然后分析最大应变单元的等效Von Mises应变-时间曲线和由应变-时间曲线一阶导得到的应变率-时间曲线，获得最大应变单元对应的最大应变率，并以此作为装药的最大应变率。

图3和图4分别为管状推进剂装药在不同时刻的等效Von Mises应力云图和应变云图。

图3 不同时刻管状推进剂装药的等效应力云图Fig.3 The equivalent stress distribution of tubular propellant charge at different time

由图3可知，随着时间的增加，装药底部应力场呈剧增趋势，应力集中区域不断向装药顶端扩展，但是上半侧分布较为有序，其值随高度的增加而降低，同一横截面位置的应力数值基本相同，下半侧应力场分布较为紊乱，较大应力主要集中在装药底端的内孔位置。其分布情况完全符合圣维南原理(Saint-Venant’s Principle)的阐述，如果把物体的一部分边界上的力变换为分布不同但等效的力，那么近处的应力分布将有显著的变化，但远处所受的影响可以不计。随着载荷的施加，应力波开始从底端向上传播， 在4ms时趋于稳定，最大等效Von Mises应力云图基本保持不变；装药最大等效Von Mises应力随时间的增加呈现振荡式增大，在4ms时刻增加到最大值18.56MPa，4ms之后装药的最大等效应力趋于稳定，但其值呈现微小的振荡，最大等效应力-时间曲线与载荷时间相似。10ms加载过程中的最大等效Von Mises应力对应的云图为4ms时刻之后的云图，即4ms时刻之后的云图为最大等效Von Mises应力云图。

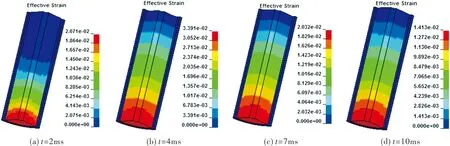
图4 不同时刻管状推进剂装药的等效应变云图Fig.4 The equivalent strain distribution of tubular propellant charge at different time

由图4可知，随着时间的增加，装药的最大等效Von Mises应变不断发生变化，由2ms时的2.071%逐渐增加，在4ms时达到最大值3.391%，并在10ms时降低为1.413%。装药上半侧应变场分布较为有序，其值随高度的增加而降低，同一横截面位置的应变数值基本相同，应变集中区域主要位于装药底端的内孔位置。10ms加载过程中的最大等效Von Mises应变对应的云图为4ms时刻的云图，即4ms时刻的云图为加载过程中的最大等效Von Mises应变云图。

在装药承受加速度载荷过程中，由于底部承受力最大，最大等效Von Mises应变发生在底端内孔附近，据此可确定装药的最大应变单元。确定4ms时刻的最大等效应变云图中最大应变单元位置，并获得最大应变单元的等效Von Mises应变-时间曲线，如图5所示。通过对等效Von Mises应变-时间曲线进行一阶导处理，获得最大应变单元的应变率-时间曲线，如图6所示。

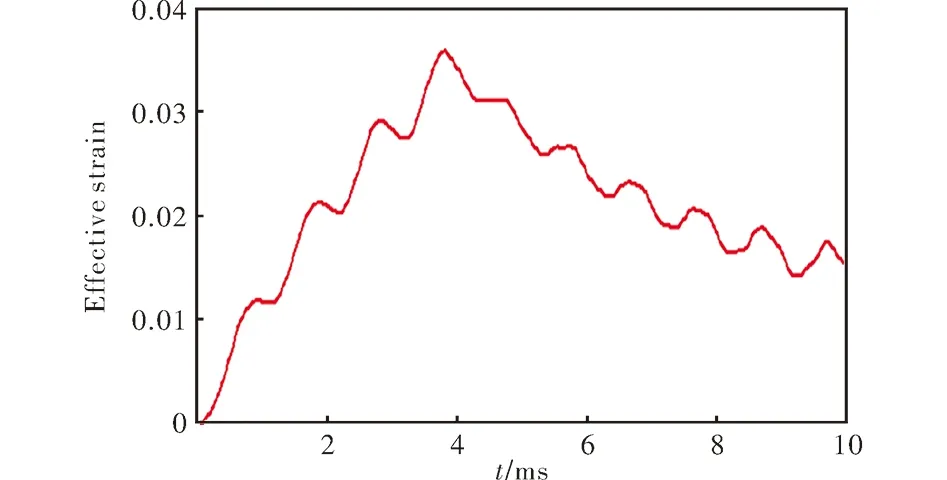
图5 等效应变-时间曲线Fig.5 Curve of equivalent strain vs.time

图6 等效应变率-时间曲线Fig.6 Curve of equivalent strain rate vs.time

由图5可知，随着时间的增加，最大应变单元的等效应变值增大，4ms时增加到最大值。在初始加速度载荷增大阶段，应变随时间的变化趋势与加载载荷随时间的变化趋势相似。当加速度载荷值稳定后，应变有一定的回弹，之后逐渐趋于稳定。但是应变在上升、回弹及稳定阶段有一定程度的波动，主要是由于计算分析时间远远小于黏弹性材料松弛时间，松弛模量在分析时间内来不及松弛。由图6可知，随着时间的增加，应变率呈现一定的波动，这是由于应变随时间的变化产生波动引起的，最大应变率发生于0.5ms附近，可确定最大应变单元的最大应变率为24s-1。

2.2 加速度对装药应变率的影响

为了获得管状装药在不同加速度条件下的最大应变率，计算了5000g、8000g、12000g和15000g加速度条件下的结构响应，获得了加载时间10ms内的最大等效应变云图，确定了最大等效应变云图中的单元，计算得到了最大应变单元的等效应变-时间曲线和由应变-时间曲线一阶导得到的应变率-时间曲线，如图7和图8所示。

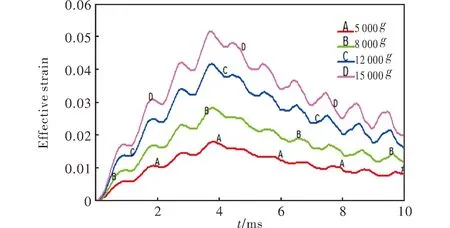
图7 不同加速度条件下等效应变-时间曲线Fig.7 Curves of equivalent strain vs.time under of different acceleration

图8 不同加速度条件下应变率-时间曲线Fig.8 Curves of equivalent strain rate vs.time under the condition of different acceleration

由图7可知，随着加速度的增加，装药的最大应变单元的最大等效应变增大，由5000g的0.017增加至15000g的0.053，但最大等效应变值均出现在4ms时刻，之后最大等效应变出现回弹并趋于稳定。不同加速度条件下的最大应变单元对应的应变-时间曲线趋势基本相同，上升段、回弹及稳定段均存在一定程度的波动，但波动次数相同，说明加速度值对波动次数基本无影响，装药与壳体之间的间隙能够满足装药外径的形变，壳体对装药的形变没有产生影响。

由图8可知，不同加速度条件下装药的应变率-时间曲线具有相同的变化趋势，加速度上升段波动4次，回弹及稳定段波动6次，与应变-时间曲线波动次数相同，但波动幅度随着加速度值的增加而增大。各加速度对应的最大应变率均发生在0.5ms附近，且随着加速度值的增加，最大应变率也逐渐增大，由5000g时的13s-1增至15000g时的35s-1。

2.3 装药尺寸对应变率的影响

在加速度10000g的条件下，选取6种装药尺寸计算最大等效应变和最大应变率，结果见表1。

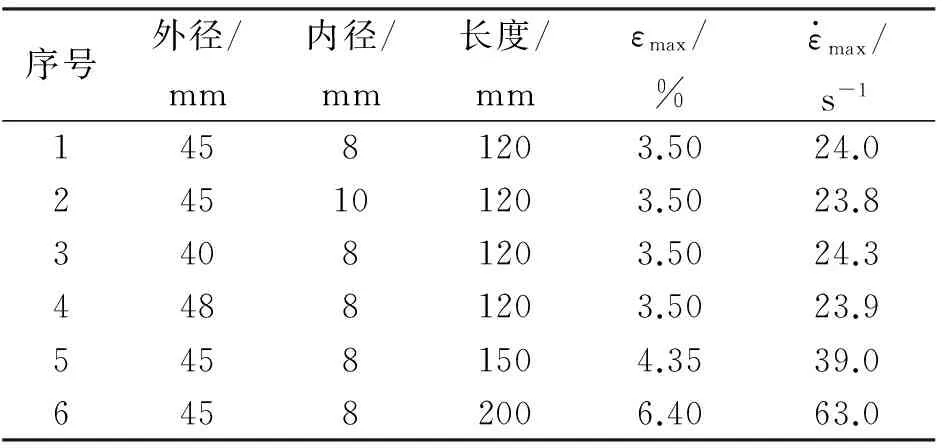
表1 不同管状装药的最大等效应变和最大应变率计算结果

由表1可知，当装药内径由8mm增至10mm时，装药最大等效应变和最大应变率基本无变化；当装药外径由40mm增至48mm时，装药最大等效应变和最大应变率变化不大，说明管状装药截面尺寸对等效应变和应变率影响效果不显著。当装药内外径不变，长度为120、150及200mm时，装药最大等效应变分别为3.5%、4.35%及6.4%，装药最大应变率为23.9、39.0及63.0s-1，等效应变和应变率最大增加了1.83%和2.63%，最大等效应变与应变率增加趋势明显，说明管状装药长度尺寸对最大等效应变及应变率影响较大，而装药内外径尺寸对最大等效应变及应变率影响较小。

3 结 论

(1)在装药承受加速度载荷过程中，底部受力和变形最大，其最大等效应力和应变均发生在底部内孔附近，分布符合圣维南原理和装药的几何构型情况。等效应力先上升后保持稳定，等效应变先上升后降低，最大等效应变云图出现在4ms时刻。

(2)随着轴向加速度由5000g增加到15000g，等效应变-时间曲线和应变率-时间曲线变化趋势基本相同，最大等效应变由1.7 %增加至5.3 %，最大值均出现在4 ms附近；最大应变率由13 s-1线性增至35 s-1，最大值出现在0.5 ms附近，处于中等应变率范围。

(3)高加速度条件下管状装药截面尺寸对最大等效应变和应变率影响效果不显著，而装药长度对最大等效应变和应变率影响效果显著。

[1] Dick W A,Heath M T.Whole system simulation of solid propellant rockets,AIAA 2002-4345[R].New York: AIAA,2002.

[2] 王狂飙.俄罗斯与西方国家的炮射导弹[J].火炮发射与控制学报,2002(4):57-61.WANG Kuang-biao.Gun-launched missiles of Russia and the west countries[J].Gun Launche & Control Journal,2002(4): 57-61.

[3] 隋欣,魏志军,王宁飞,等.炮射导弹发射过程中装药衬垫材料对抗过载能力的影响计算分析[J].兵工学报,2009,30(6):709-713.SUI Xin,WEI Zhi-jun,WANG Ning-fei,et al.Analysis of effect of the pad material on stress in the grain during launching artillery missile[J].Acta Armamentarii,2009,30(6): 709-713.

[4] Zhuo Ch,Feng F,Wu X.Development process of muzzle flows including a gun-launched missile[J].Chinese Journal of Aeronautics,2015,31(2): 385-393.

[5] 张奇,闫华,白春华.装药发射过载动力学研究[J].振动与冲击,2003,22(2):78-80.ZHANG Qi,YAN Hua,BAI Chun-hua.Research on dynamics of launching over-loading of charge[J].Journal of Vibration and Shock,2003,22(2): 78-80.

[6] 李亮亮，沈飞，屈可朋，等.炸药装药在不同应变率响应条件下的安全性研究进展[J].火炸药学报,2016,39(4):14-22.LI Liang-liang,SHEN Fei,QU Ke-peng,et al.Progress of study on the safety of explosive charge under different strain-rate conditions[J].Chinese Journal of Energetic & Propellants(Huozhayao Xuebao),2016,39(1):14-22.

[7] 李尚昆，黄西成，王鹏飞.高聚物黏结炸药的力学性能研究进展[J].火炸药学报，2016，39(4)：1-11.LI Shang-kun,Huang Xi-cheng,WANG Peng-fei.Recent advances in the investigation on mechanical properties of PBX[J].Chinese Journal of Explosives and Propellants(Huozhayao Xuebao),2016,39(4):1-11.

[8] Field J E,Walley S M,Proud W G,et al.Review of experimental techniques for high rate deformation and shock studies[J].International Journal of Impact Engineering,2004,30: 725-775.

[9] Siviour C R,Walley S M,Proud W G,et al.The high strain rate compressive behavior of polycarbonate and polyvinylidene difluoride[J].Polymer,2005,46(26): 12546-12555.

[10] Yildirim H C,Özüpek S.Structural assessment of a solid propellant rocket motor: effects of aging and damage[J].Aerospace Science & Technology,2011,15(8): 635-641.

[11] 魏卫,王宁飞.高加速度冲击下固体推进剂药柱轴向形变的数值模拟[J].固体火箭技术,2003,26(2):42-45.WEI Wei,WANG Ning-fei.Numerical simulation for the axial deformation of solid propellant grains under the high acceleration shock[J].Journal of Solid Rocket Technology,2003,26(2): 42-45.

[12] 魏卫,王宁飞.轴向高过载下固体推进剂结构完整性数值模拟[J].火炸药学报,2004,27(1):53-55.WEI Wei,WANG Ning-fei.Numerical simulation of structural integrity for solid propellants under axial high overloads[J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2004,27(1): 53-55.

[13] 屈可朋，沈飞，肖玮，等.RDX基PBX炸药的力学行为和损伤模式[J].火炸药学报，2012，35(5)：38-40.QU Ke-peng,SHEN Fei,XIAO Wei,et al.Mechanical behavior and damage mode of RDX-based PBX explosive[J].Chinese Journal of Explosives and propellants(Huozhayao Xuebao),2012,35(5):38-40.

[14] 龚建良,刘佩进,李强.基于能量守恒的HTPB推进剂非线性本构关系[J].含能材料,2013,21(3): 325-329.GONG Jian-liang,LIU Pei-jin,LI Qiang.Nonlinear constitutive relation of HTPB propellant based on the first law of thermodynamics[J].Chinese Journal of Energetic Materials,2013,21(3): 325-329.

[15] 张晓宏,郑晓亚,李宏岩,等.含人工脱粘层固体装药结构应力应变场分析[J].应用力学学报,2012,29(4):426-430.ZHANG Xiao-hong,ZHENG Xiao-ya,LI Hong-yan,et al.Stress and strain analysis for solid rocket motor grains with stress-release boot[J].Chinese Journal of Applied Mechanics,2012,29(4): 426-430.

Research on Simulating the Strain Rate of Tubular Propellant Charge under the Condition of Launching Acceleration Load

LI Meng,ZHAO Feng-qi,XU Si-yu,PEI Qing,HAO Hai-xia,YAO Er-gang,JIANG Han-yu

(Science and Technology on Combustion and Explosion Laboratory,Xi′an Modern Chemistry Research Institute,Xi′an 710065,China)

The finite element model was established by LS-DYNA software,the strain and strain rate of tubular propellant charge under the condition of launching acceleration were simulated and calculated.The structure response of charge under the condition of 10000g(gis the acceleration of gravity )was analyzed.The effect of different acceleration load (5000-15000g)and structure size of charge on the maximum equivalent strain and strain rate was discussed.The results show that in the supporting acceleration load process for charge,the maximum equivalent strain and strain rate occur near the bottom of the inner hole.With increasing the axial acceleration from 5000gto 15000g,the change trend of equivalent strain-time curve and strain rate-time curve is basicallly the same.The maximum strain rate increases linearly from 13 s-1to 35s-1,which is in medium strain rate range.With increasing the charge length from 120mm to 200mm,the maximum equivalent strain and maximum strain rate increase by 1.83% and 2.63%,respectively.

tubular propellant charge; launching acceleration; strain rate; numerical simulation

10.14077/j.issn.1007-7812.2017.01.015

2016-09-23；

2016-12-17

国家自然科学基金(21473130)

李 猛(1979-)，男，硕士，副研究员，从事固体推进剂性能计算技术研究。E-mail：dahai99-2005@163.com

TJ55;V448.15+3

A

1007-7812(2017)01-0075-06