基于贝叶斯理论的水文多模型预报
2017-02-27周正叶爱中马凤杜超
周正+叶爱中+马凤+杜超

摘要:水文预报对于防洪、抗旱以及水资源调度等具有重要意义。水文预报通常依靠水文模型来完成,由于受到不同流域特点、产汇流机制等的限制,每个水文模型都具有各自的特点及适用区域。单一模型具有非常大的水文预报不确定性,为了解决单一模型局限性的问题,多模型水文预报常作为降低水文预报不确定性有效方法之一。选用三种常见的水文模型:时变增益水文模型、新安江模型和萨克拉门托模型,在珠江飞来峡流域进行分布式建模,采用相同的输入与初始场,三个模型独立进行模拟,然后对比三个模型的结果,并进行贝叶斯多模型加权平均和简单平均得到多模型平均结果,研究结果表明,贝叶斯模型处理后的结果要比单个模型模拟结果和简单平均处理后的结果准确率高。
关键词:飞来峡;水文预报;不确定性;贝叶斯多模型
中图分类号:TV124文献标志码:A文章编号:1672-1683(2017)01-0043-06
Abstract:Hydrological forecast is very important for flood control,drought resistance and water resources regulation.It is usually based on model simulation.Each hydrological model has its own characteristics and feasible basin.Multi-model hydrological forecast is one of the effective methods to reduce the forecasting uncertainty.This paper chose three commonly used hydrological models:time-variant gain hydrological model,Xin′anjiang model,and Sacramento model.The case study was on Feilaixia basin of Pearl River.The three hydrological models were used for independent simulation with the same input and initial value.Then,BMA and SMA were run on the three models′results.The research results show that the BMA results are better than the results from single model simulation.
Key words:Feilaixia;hydrological forecast;uncertainty;Bayesian model averagin
水文預报不确定性主要来源于水文模型的不确定性。为了降低水文模型的不确定性,越来越多的水文模型被提出并应用到不同流域[1]。其中应用比较广泛的有萨克拉门托模型(Sacramento model,SAC)[2],新安江模型(Xin An Jiang,XAJ)[3],和时变增益水文模型(Time Variation Gain Model,DTVGM)[4]等。然而每个模型都具有各自的优势与局限性,而且由于水文过程的复杂性,导致水文模型不确定性日益凸显。对此,广大水文学者提出多模型信息融合的方法。该方法可以降低单个模型的偏差,使模拟更接近于观测值。目前,水文预报综合处理方法主要有简单平均法(Simple Model Averaging,SMA)、加权平均法、神经网络和模糊推理法等[5-10]。其中,贝叶斯加权平均方法(Bayesian Model Averaging,BMA)最为广泛使用。贝叶斯方法是基于贝叶斯理论而发展起来用于解决统计问题的方法。随着科学技术的发展,贝叶斯方法在统计学[11]成功应用之后,逐渐发展到计量经济学[12],社会学[13]等方面。在气象领域,贝叶斯最大似然方法被应用于预测温度及降水的概率分布[14],Ma[15]等人通过改变BMA目标函数,将其应用于NMME季节性降水集合预报。近年来,BMA方法被应用于水文领域:Neuman[16]提出利用最大似然贝叶斯平均方法分析地下水模型不确定性来优化水文预报的方法,Kavetski[17]等人通过使用贝叶斯误差分析方法评估输入降雨不确定性对VIC模型模拟的影响。Zhang[18]利用BMA方法对SWAT水文模型的拟定和不确定性分析。为了得到对水文模型更为优化的处理结果,Raftery[19]等采用BMA对多个数字天气预报模型权重进行最优化处理,Duan[20]通过贝叶斯方法进行多模型水文集合预报,并得到比较好的结果。
基于BMA处理后的高精度预报[21],本文将BMA方法应用于飞来峡流域进行模拟预报,并与DTVGM模型、XAJ模型、SAC模型及SMA方法处理结果进行对比,分析多模型方法的预报结果。
1 流域概况
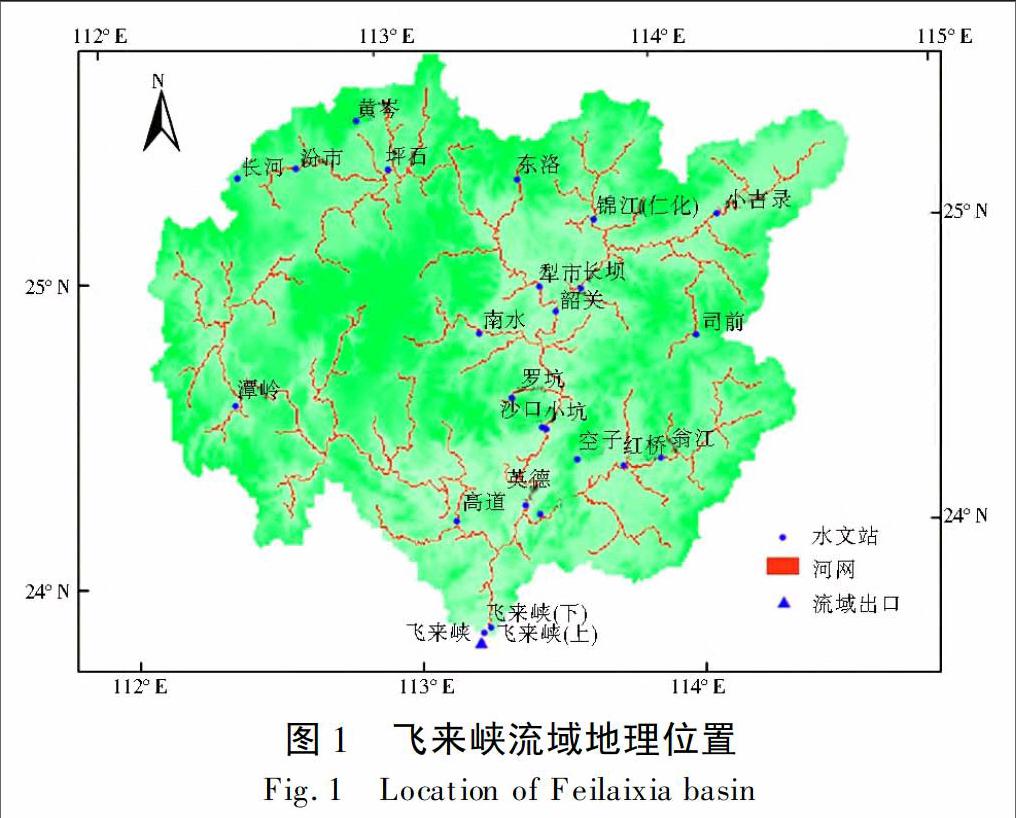
飞来峡流域位于珠江第二大水系北江的中上游,控制集水面积为34 097 km2,大约为北江流域面积的73%。该流域属于热带和亚热带气候区,且由于东南和西南季风的影响,降水不均,汛期平均降水量为1 224 mm,约占全年降水量的70%[22-23],因此时常会遭受洪水灾害。流域概况见图1。
本文以飞来峡流域为研究对象,采用100 km2河网阈值将流域划分为146个子流域。收集到气象数据为1980年-2009年日降水、气温和蒸发数据。流量采用流域出口1980年-2009年日流量数据,时间序列长度为30年,其中1980年-1999年作为拟定期,2000年-2009年作为验证期。
2 模型方法介绍
2.1 水文模型介绍
2.1.1 分布式时变增益水文模型
时变增益模型是夏军[24-25]于1989年-1995年期间提出的一种研究方法,建立了降水-土壤湿度-产流之间的非线性关系。随着GIS技术的发展,时变增益模型发展为分布式时变增益水文模型,并且仍在不断地改进。该模型可以根据时间尺度分为月尺度、日尺度和小时尺度。
2.1.2 新安江模型
新安江模型是于20世纪60、70年代由我国水文工作者研制开发的水文模型,主要包括蒸发计算模型、产流模型、三水源划分模型以及汇流模型。其理论主要基于蓄满产流理念,即土壤湿度达到田间持水量以后才开始进行产流,在未达到田间持水量时,则不进行产流,所有的降水都会被土壤吸收,该模型被广泛的应用在湿润与半湿润的中型或者大型流域[26-28]。
2.1.3 萨克拉门托模型
萨克拉门托流域水文模型是集总参数型、连续运算的确定性流域水文模型,由美国天气局水文办公室萨克拉门托预报中心于20世纪70年代初期,于第IV号斯坦福模型基础上改进和发展。萨克门托模型的核心主要为土壤含水量模型,结构分为上、下两层,通过计算输入降水模拟蒸散发量、地表径流以及下渗水量[29-31]。
2.2 BMA和SMA介绍
BMA (Bayesian Model Averaging,BMA)是一个通过加权平均不同模型的预报值得到更可靠的综合预报值的数学方法[32]。贝叶斯所选定的模型空间中,最佳模型并不确定,根据贝叶斯模型平均法基本理论,可以给出模型变量的概率密度函数,通过对实测和模拟流量数据的正态分位变化,进行期望最大化(EM)算法,进而通过正态反转换得到空间对应关系,即对不同模型所占权重进行加权平均,从而计算出BMA模拟流量[33]。
简单平均法(Simple Model Averaging,SMA)即为模型模拟流量的简单平均,每个模型所占的权重相同。
2.3 模型驗证指标
为了对模型模拟结果进行合理的评价,采用相关系数(R)、纳什效率系数(NSE、NSEB[35]、NSEI[36])、偏差(rBias)和均方根误差(RMSE)评价指标(见表1)。其中rBias接近于0说明模型模拟总量和观测总量一致,NSE越接近于1说明模型整体可靠性越高。
由于NSE受模拟洪峰影响较大,即NSE的高低由模拟洪峰的准确度主导:洪峰模拟越好,则NSE越高,而枯水期的模拟对NSE的影响较小,因此本文增加NSEI指标,即NSEI越接近于1则枯水流量模拟精度越高。通过NSE和NSEI两个指标可以判断整体模拟效果。此外,本文增加NSEB指标,NSEB越接近于1说明相对于参考系统(本文采用多年平均流量)更优。
3 结果分析与讨论
3.1 模型拟定与验证
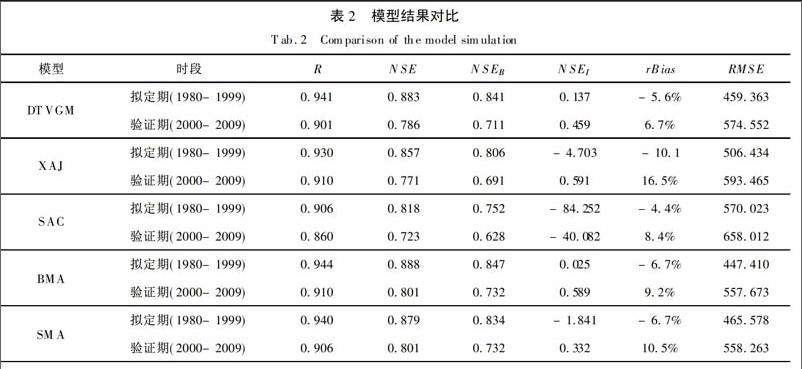
本文选定1980年-1999年为拟定期,2000年-2009年为验证期,分别采用分布式时变增益水文模型、新安江模型以及萨克拉门托模型进行模拟[34],在得到模拟流量之后分别用BMA和简单算术平均对模型结果进行后处理,从而判断模型的模拟性能,结果见表2。
在拟定期,三个模型模拟的相关系数均达到了0.9以上,纳什效率系数在0.85以上,偏差均在±5%左右,表明三个模型较高的可靠性和较小的模拟偏差。
在验证期,DTVGM和新安江模型模拟结果相关系数在0.9以上,纳什效率系数在0.75以上,略优于SAC模型,三个模型均表现出比较好的模拟结果说明了拟定期参数的合理性。倒数纳什效率系数(NSEI)在拟定和验证期均不太高,尤其是SAC模型出现负值,说明水文模型对枯季流量模拟精度较差。
图2和图3分别给出了拟定期和验证期几个模型的日径流模拟过程图,可以看出,分布式时变增益水文模型、新安江模型以及萨克拉门托模型整体模拟效果比较好,洪峰及峰现时间同观测一致。
3.2 多模型比较分析
从表2可看出BMA和SMA的结果相对优于三个模型独立的模拟结果,而BMA的结果要优于简单平均的处理结果。通过BMA权重分析,充分考虑三个模型的精度,DTVGM、新安江模型和SAC模型所占权重分别为0.729、0.252、0.019,其中DTVGM模型所占权重最大,说明该模型模拟结果要优于其余两个模型,符合表2指标。SAC模型由于在枯水期流量模拟精度较差,所以权重较低。简单算术平均方法三个模型的权重相等,虽然在一定程度上对最终模拟效果进行了优化,但是缺乏对模型信息最大化的利用,并未考虑每个模型各自的精度,因此处理效果比BMA差。
为了更清楚的展示BMA和单个模型模拟结果,图4做出了多个模型在验证期10年数据的日平均流量,由图4可以发现BMA处理后的结果更接近于实测流量,尤其在低水期:1月1日-3月1日及9月15日-12月31日时间段内BMA优化效果更为明显。
4 小结
本研究探讨了多模型水文预报应用于实际流域的可行性,飞来峡流域属于湿润地区,三个模型对洪水都有比较好的模拟结果,其中DTVGM模拟结果最好,其次为XAJ模型和SAC模型,但在枯水期模拟存在一定的误差,经BMA和SMA处理后的结果要优于单个模型的模拟结果。BMA处理方法充分考虑了每个模型的精度,最大程度利用了模型信息,给出了每个模型所占权重,并具有较高相关系数和最小的均方根误差,较之于简单的算数平均方法,具有更高的精度和稳定性,并且在枯水期模拟效果更为明显。
参考文献(References):
[1] 李怀恩,沈晋.现行几个主要产流模型的剖析[J].水文,1996(1):14-23.(LI Huai-en,SHEN Jin.Analysis of the main runoff yield models[J].Hydrology,1996(1):14-23.(in Chinese))
[2] Burnash R J C.Chapter 10:the NWS river forecast system-catchment modeling[M],in Computer Models of Water Shed Hydrology,edited by Singh V P,Water Resources Publications,Littleton Colo,1995.
[3] Zhao R J.The Xinanjiang model applied in China[J].Journal of Hydrology,1992,135(1):371-381.DOI:10.1016/0022-1694(92)90096-E.
[4] Xia J.A system approach to real time hydrological forecasts in watersheds[J].Water International,27(1):87-97.DOI:10.1080/02508060208686981.
[5] 路志英,趙智超,郝为,等.基于人工神经网络的多模型综合预报方法[J].计算机应用,2004,24(4):50-51,88.(LU Zhi-ying,ZHAO Zhi-chao,HAO Wei,et al.Multi-model ensemble forecast method based on ANN[J].Computer Applications,2004,24(4):50-51,88.(in Chinese))
[6] 熊立华,郭生练,叶凌云.自适应神经模糊推理系统(ANFIS)在水文模型综合中的应用[J].水文,2006,26(1):38-41.(XIONG Li-hua,GUO Sheng-lian,YE Ling-yun.Application of ANFIS in the combination of hydrological models[J].Journal of China Hydrology,2006,26(1):38-41.(in Chinese)) DOI:10.3969/j.issn.1000-0852.2006.01.009.
[7] Shamseldin A Y,O′Connor K M,Liang G C.Methods for combining the outputs of different rainfall-runoff models[J].Journal of Hydrology,1997(1):203-229.DOI:10.1016/S0022-1694(96)03259-3.
[8] See L,Abrahart R J.Multi-model data fusion for hydrological forecasting[J].Computers & Geosciences,2001,27(8):987-994.DOI:10.1016/S0098-3004(00)00136-9.
[9] Talei A,Chua L H C.Influence of lag time on event-based rainfall-runoff modeling using the data driven approach[J].Journal of Hydrology,438(1):223-233.DOI:10.1016/j.jhydrol.2012.03.027.
[10] Astray G,Soto B,Lopez D,et al.Application of transit data analysis and artificial neural network in the prediction of discharge of Lor River,NW Spain[J].Water Science and Technology,73(7):1756-1767.DOI:10.2166/wst.2016.002.
[11] Efron B.Bayesian,frequentists,and scientists[J].Journal of the American Statistical Association,2005,100(469):1-5.DOI:10.1198/016214505000000033.
[12] Stock J H,Watson M W.Macroeconomic forecasting using diffusion indexes[J].Journal of Business & Economic Statistics,2002,20(2):147-162.DOI:10.1198/073500102317351921.
[13] Zheng T,Salganik M J,Gelman A.How many people do you know in prison? Using Overdispersion in count data to estimate social structure in networks[J].Journal of the American Statistical Association,2006,101(474):409-423.DOI:10.1198/016214505000001168.
[14] Duan Q Y,Phillips T J.Bayesian estimation of local signal and noise in multimodel simulations of climate change[J].Journal of Geophysical Research,2010,115(D18):D18123.DOI:10.1029/2009JD013654.
[15] Ma F,Ye A Z,Deng X X,et al.Evaluating the skill of NMME seasonal precipitation ensemble predictions for 17 hydroclimatic regions in continental China[J].International Journal of Climatology,2016,36(1):132-144.DOI:10.1002/joc.4333.
[16] Neuman S P.Maximum likelihood Bayesian averaging of uncertain model predictions[J].Stochastic Environmental Research and Risk Assessment,2003,17(5):291-305.DOI:10.1007/s00477-003-0151-7.
[17] Kavetski D,Kuczera G,Franks S W.Bayesian analysis of input uncertainty in hydrological modeling:2.Application[J].Water Resources Research,2006,42(3).DOI:10.1029/2005WR004376.
[18] Zhang X S,Srinivasan R,Bosch D.Calibration and uncertainty analysis of the SWAT model using genetic algorithms and Bayesian model averaging[J].Journal of Hydrology,2009,374:307-317.DOI:10.1016/j.jhydrol.2009.06.023.
[19] Raftery A E,Gneiting T,Balabdaooui F,et al.Using Bayesian model averaging to calibrate forecast ensembles[J].Monthly Weather Review,2005,133(5):1155-1174.DOI:10.1175/MWR2906.1.
[20] Duan Q Y,Ajami N K,Gao X G,et al.Multi-model ensemble hydrologic prediction using Bayesian model averaging[J].Advances in Water Resources,2007,30(5):1317-1386.DOI:10.1016/j.advwatres.2006.11.014.
[21] 梁忠民,戴荣,王军,等.基于贝叶斯模型平均理论的水文模型合成预报研究[J].水力发电学报,2010,29(2):114-118.(LIANG Zhong-min,DAI Rong,WANG Jun,et al.Study on forecast combination of different hydrological models by Bayesian model averaging[J].Journal of Hydroelectric Engineering,2010,29(2):114-118.(in Chinese))
[22] Wu C H,Huang G R.Changes in heavy precipitation and floods in the upstream of the Beijiang River Basin,South China[J].International Journal of Climatology,2015,35(10):2978-2992.DOI:10.1002/joc.4187.
[23] Wu C H,Huang G R,Yu H J,et al.Spatial and temporal distributions of trends in climate extremes of the Feilaixia catchment in the upstream area of the Beijiang River Basin,South China[J].International Journal of Climatology,2014,34(11):3161-3178.DOI:10.1002/joc.3900.
[24] 葉爱中,段青云,徐静.水文集合预报概述及模型案例[M].北京:中国水利水电出版社,2014.(YE Ai-zhong,DUAN Qing-yun,XU Jing.Overview of hydrological ensemble forecast and model cases[M].Beijing:China Water & Power Press,2014.(in Chinese))
[25] Ye A Z,Duan Q Y,Zeng H J,et al.A distributed time-variant gain hydrological model based on remote sensing[J].Journal of Resources and Ecology,2010,1(3):222-229.DOI:10.3969/j.issn.1674-764x.2010.03.005.
[26] 詹道江,叶守泽.工程水文学[M].北京:水利电力出版社,2004.(ZHAN Dao-jiang,YE Shou-ze.Engineering hydrology[M].Beijing:China Water & Power Press,2008.(in Chinese))
[27] 李藝婷,张万顺,朱齐艳,等.新安江模型产流模式在山区型和平原型水库入库径流量中的模拟与应用[J].水资源与水工程学报,2007,18(1):33-36.(LI Yi-ting,ZHANG Wan-shun,ZHU Qi-yan,et al.Application of runoff generation mode of Xinanjiang model in mountain and plain reservoir runoff simulation[J].Journal of Water Resources and Water Engineering,2007,18(1):33-36.(in Chinese)) DOI:10.3969/j.issn.1672-643X.2007.01.008.
[28] Ju Q,Yu Z B,Hao Z C,et al.Division-based rainfall-runoff simulations with BP neural nnetworks and Xinanjiang model[J].Neurocomputing,2009,72(13):2873-2883.DOI:10.1016/j.neucom.2008.12.032.
[29] 熊剑锋,张树全.萨克拉门托水文模型在天生桥洪水预报的应用[J].云南水力发电,1999,15(1):4-7.(XIONG Jian-feng,ZHANG Shu-quan.Application of Sacramento hydrological model in flood forecast for Tianshengqiao-I hydropower project[J].Yunnan Water Power,1999,15(1):4-7.(in Chinese))
[30] 张卫华,李雨,魏朝富,等.不同水文模型在Broken流域的比较研究[J].西南师范大学学报:自然科学版,2011,36(4):211-216.(ZHANG Wei-hua,LI Yu,WEI Chao-fu,et al.A comparative study of different hydrological model and their application in Broken Catchment[J].Journal of Southwest China Normal University (Natural Science Edition),2011,36(4):211-216.(in Chinese)) DOI:10.13718/j.cnki.xsxb.2011.04.007.
[31] Carpenter T M,Georgakakos K P.Intercomparison of lumped versus distributed hydrologic model ensemble simulations on operational forecast scales[J].Journal of Hydrology,2006,329(1):174-185.DOI:10.1016/j.jhydrol.2006.02.013.
[32] 董磊华,熊立华,万民.基于贝叶斯模型加权平均方法的水文模型不确定性分析[J].水利学报,2011,42(9):1065-1074.(DONG Lei-hua,XIONG Li-hua,WAN Min.Uncertainty analysis of hydrological modeling using the Bayesian Model Averaging Method[J].Journal of Hydraulic Engineering,2011,42(9):1065-1074.(in Chinese)) DOI:10.13243/j.cnki.slxb.2011.09.002.
[33] Hoteling J A,Raftery M D,Volinsky A E.Bayesian Model Averaging:a tutorial[J].Statistical Science,1999,14(4):382-401.DOI:10.1214/ss/1009212814.
[34] 夏军,王纲胜,谈戈,等.水文非线性系统与分布式时变增益模型[J].中国科学,2004,34(11):1062-1071.(XIA Jun,WANG Gang-sheng,TAN Ge,et al.Nonlinear hydrological system and distributed time variant gain modeling[J].Science in China Series D:Earth Sciences,2004,34(11):1062-1071.(in Chinese)) DOI:10.3969/j.issn.1674-7240.2004.11.009.
[35] Schaefli B,Gupta H V.Do Nash values have value?[J].Hydrological Processes,2007,21(15):2075-2080.DOI:10.1002/hyp.6825.
[36] Pushpalatha R,Perrin C,Le Moine N,et al.A review of efficiency criteria suitable for evaluating low-flow simulations[J].Journal of Hydrology,2012,420:171-182.DOI:10.1016/j.jhydrol.2011.11.055.
