Burgers方程的新的精确解

李 伟

(渤海大学 数理学院, 辽宁 锦州 121013)

Burgers方程的新的精确解

李 伟

(渤海大学 数理学院, 辽宁 锦州 121013)

求非线性偏微分方程的精确解非常重要,Burgers方程是一个模拟冲击波的传播和反射的非线性偏微分方程,它在非线性偏微分方程中具有重要地位。给出了Burgers方程的全新的精确解,具体的方法如下:首先,对方程进行行波变换;然后,分别利用双曲函数法和改进的双曲函数法给定它不同形式的拟解,其中拟解的项数由齐次平衡法确定,拟解中的函数满足Riccati方程;再将拟解代入行波变换后的方程,得到一个方程组;最后,借助计算机代数系统Mathematica解此方程组,确定拟解,即为全新的精确解。这种方法求得的Burgers方程的精确解,包含了一些文献的结果,也修正了某些文献的结论。这种方法可以用来求一系列偏微分方程的精确解。

行波变换; 精确解;Burgers方程

0 引 言

非线性偏微分方程(组)的解法受到如数学、物理学、工程学和生物学等各个学科工作者的广泛重视,为了寻求它们的解法,科研工作者们做了大量有益的工作,得到了一些行之有效的求解方法,如分离变量法、反散射方法、Backlund变换法、Darboux变换法、tanh函数法、Riccati方程法等[1-8]。本文借助行波变换法[9-10]、双曲函数法、改进的双曲函数法[11-12]和齐次平衡法[13-15],获得了Burger的新的精确解。

1 Burgers的新的精确解

Burger方程如下:

(1)

首先,假定(1)有如下形式的解:

(2)

k是待定常数。 将式(2)代入式(1)整理化简得

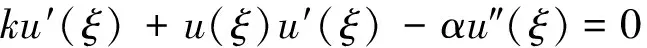
(3)

对式(3)积分,积分常数取0,式(3)变为

(4)

1.1 利用双曲函数法

假定式(4)有如下形式的解:

(5)

其中:M是待定的正整数;ai(i=0,1,2,…,M)是待定常数;φ(ξ)是函数,满足Riccati方程,即

(6)

P,Q是任意常数。那么式(6)有如下形式的解:

若PQ<0,

(7)

C是常数。

借助齐次平衡法,得到方程

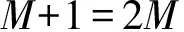
(8)

解得M=1

因此,式(5)的具体形式为

(9)

将式(6)和式(9)代入式(4),得到方程:

(10)

令φi(ξ),(i=0,1,2,)的系数为0,得到关于ai(i=0,1,…)和k的代数方程组,即

(11)

利用Mathematica运算,求得如下形式的解:

(12)

将式(7),式(9)和式(12)代入式(2),就得到式(1)的新的精确解,即

(13)

(14)

1.2 利用改进的双曲函数法

假定(4)有如下形式的解:

(15)

其中:M是待定的正整数;ai(i=0,1,2,…,2M)是待定常数。φ(ξ)也满足Riccati方程(6),借助齐次平衡法,仍然有M=1。因此式(15)的具体形式为

(16)

将式(6)和式(16)代入式(4),得到方程:

(17)

令φi(ξ),(i=0,±1,±2,)的系数为0,得到关于ai,(i=0,1,2)和k的代数方程组,利用Mathematica运算,求得如下形式的解:

(18)

将式(7),式(16)和式(18)代入式(2),又就得到式(1)的新的精确解,即

(19)

(20)

2 结 论

利用行波变换法、双曲函数法、改进的双曲函数法和齐次平衡法,获得了Burgers的全新精确解。这种方法也可用于解其他非线性偏微分方程(组)。Burgers的全新精确解的获得将为近似计算、定理分析等现实问题提供帮助。

[ 1 ]李德生,张鸿庆. 一类高维耦合的非线性演化方程的简单求解[J]. 物理学报, 2004,53(6):1636-1638.

[ 2 ]李翊神. 孤子与可积系统[M]. 上海:上海科技教育出版社, 1999:45-65.

[ 3 ]陈登远. 孤子引论[M]. 北京:科学出版社, 2006:14-44.

[ 4 ]谷超豪,胡和生,周子翔. 孤立子理论中的达布变换及几何应用[M]. 上海:上海科学技术出版社, 1999:3-35.

[ 5 ]张春荣. 扩展齐次平衡法与Backlund变换[J]. 光子学报, 2002,31(11):1348-1351.

[ 6 ]邢秀芝,吴景珠. 广义变系数Burgers方程的显示精确解[J]. 河南大学学报(自然科学版), 2011,41(6):562-566.

[ 7 ]桑波,伊继金,刘健文. 常系数线性微分方程组的解矩阵[J]. 沈阳师范大学学报(自然科学版), 2010,28(3):343-346.

[ 8 ]李向正,王跃明,李晓燕,等. 组合KdV-Burgers方程的一种解法[J]. 河南科技大学学报, 2003,24(4):104-107.

[ 9 ]李志斌. 非线性数学物理方程的行波解[M]. 北京:科技出版社, 2006.

[10]李伟.Boussinesqequations的新的精确解[J]. 重庆理工大学学报, 2015,29(6):151-154.

[11]WAZWAZAM.Theextendedtanhmethodfornewsolitonsolutionsforthefifth-orderKdVequations[J].ApplMathComput, 2007,84(2):1002-1014.

[12]GOMEZCA.ThecoleHopetransformationandimprovedtanh-cothmethedappliedtonewintegrablesystem[J].ApplMathComput, 2008,20(4):957-962.

[13]王明亮,李志斌,周宇斌. 齐次平衡原则及其应用[J]. 兰州大学学报, 1999,35(3):8-16.

[14]范恩贵,张鸿庆. 非线性孤子方程的齐次平衡法[J]. 物理学报, 1998,47(3):356-362.

[15]王明亮,白雪. 齐次平衡原则与BTs[J]. 兰州大学学报, 2000,36(3):12-17.

ExactsolutionsofBurgers

LI Wei

(CollegeofMathematical,BohaiUniversity,Jinahou121013,China)

Itisveryimportanttofindtheexactsolutionofnonlinearpartialdifferentialequations.Burgersequationisanonlinearpartialdifferentialequationforsimulatingthepropagationandreflectionofshockwaves.Burgersequationplaysanimportantroleinnonlinearpartialdifferentialequations.AgreatamountofworkhasbeendonetoobtaintheexactsolutionoftheBurgersequation.Inthispaper,weobtainnewexactsolutionoftheBurgersequation.Firstly,thetravelingwavetransformationoftheBurgersequationiscarriedout;Secondly,Respectivelybyusinghyperbolicfunctionmethodandimprovedhyperbolicfunctionsmethod,differentformsofquasisolutionwasgiven,thenumberinthesolutionisdeterminedbythehomogeneousbalancemethod,functionwiththeRiccatiequation;Finally,thequasisolutionisdeterminedbythecomputeralgebrasystemMathematica,whichisanewexactsolution.Theexactsolutionnotonlycontainstheresultsofsomeliterature,butalsorevisessomeoftheconclusionsoftheliterature.Thismethodcanbeusedtofindaseriesofexactsolutionsofpartialdifferentialequations.

travelling-wavetransform;exactsolutions;Burgersequation

2016-10-29。

国家自然科学基金资助项目(11547005)。

李 伟(1977-),男,辽宁锦州人,渤海大学讲师,硕士。

1673-5862(2017)01-0073-03

O

A

10.3969/j.issn.1673-5862.2017.01.013