电动工具阶梯轴圆角过渡半径的优化设计

王浩琦，邵葆霖

（ 1.上海理工大学，上海 200093；2.上海江南长兴重工有限责任公司，上海 201913 ）

电动工具阶梯轴圆角过渡半径的优化设计

王浩琦1，邵葆霖2

（ 1.上海理工大学，上海 200093；2.上海江南长兴重工有限责任公司，上海 201913 ）

通过ANSYS软件建立不同直径和过渡圆角半径的阶梯轴三维模型，计算阶梯轴模型在纯扭转条件下的应力、应变；找出每个阶梯轴的最大应力及其存在的位置。根据计算结果，绘制最大应力随过渡圆角半径变化的曲线和随过渡圆角半径与小径比值的变化曲线，分析阶梯轴结构对应力集中程度的影响。

阶梯轴；应力集中；有限元；过渡圆角

0 引言

在电动工具阶梯轴设计过程中，选取合适的过渡圆角可有效减轻应力集中。常见的应力集中通常出现在物体形状发生急剧变化的缺口、孔洞、沟槽以及刚性约束处，致使物体产生疲劳裂纹继而引发疲劳破坏，降低零件的使用寿命，对于脆性材料制成的零件或可直接引发静载断裂。所以，在阶梯轴的设计中应对此格外注意。本文通过ANSYS软件应用有限单元法，分析在纯扭转条件下不同过渡圆角半径对阶梯轴应力的影响，提出阶梯轴在使用圆角过渡时，过渡圆角半径大小的选择依据。

1 概述

有限元法（finite element method）是一种高效能、常用的数值计算方法。它把复杂的结构或者连续体按照一定的方法离散成有限个单元，并在每个单元中按照一定的原则设定有限个节点，各单元彼此在节点处连续而组成整体，先对单元进行特性分析，然后根据各单元在节点处的协调条件建立平衡方程或刚度方程，综合后作整体分析。

2 应用

有限元法分析过程可分为：

1）结构离散化（单元划分）

即把复杂的结构或连续体细分为有限个微小单元的组合，各单元彼此在节点处连续而组成整体。

2）选择位移模式

在分析连续体时，用节点位移的坐标形式表示出单元体的位移、应变和应力的简单函数，称这种节点位移函数为形函数

3）分析单元的力学特性

利用几何方程：由位移表达式导出用点位移表示单元应变的关系式

式中 {ε}—单元内任一点应变列阵

利用物理方程，由应变的表达式导出用节点位移表示单元应力的关系式

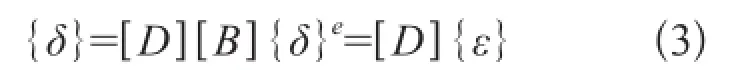
式中 {δ}—单元内任一点应力列阵

[D]—材料弹性矩阵

利用虚功原理建立单元的刚度方程，是作用于单元上的节点力和节点位移之间的关系式

式中 [K]—单元刚度矩阵

4）计算等效节点力

作用在单元边界上的表面力、体积力、集中力等都需要等效移置节点，即原载荷与节点载荷在任何虚位移上的虚功都相等。

5）组装总刚度阵，建立结构的平衡方程

两方面内容：组装总刚以及组装总的载荷列阵

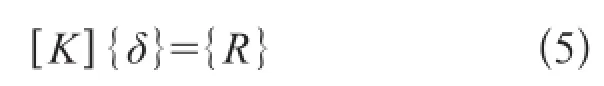
6）求解结点的位移和计算单元应力

3 影响

3.1 过渡圆角半径大小对阶梯轴的影响

3.1.1 模型几何尺寸

阶梯轴的结构模型，如图1所示。

图1 带过渡圆角的阶梯轴结构模型

圆轴的具体尺寸如下：

1）阶梯轴第一段长度为50mm，直径D保持30mm不变；

2）第二段长度为100mm，直径d分别为6mm、10mm、15mm、20mm；

3）过渡圆角半径r分别为0.5mm、0.8mm、1.0mm、2.0mm、3.0mm、4.0mm、5.0mm。

利用ANSYS软件建立实体模型并对阶梯轴进行分析。

3.1.2 材料数据

阶梯轴采用SOLID185单元进行网格划分，材料为线弹性材料45#钢，其中弹性模量为2.06+E11Pa，泊松比为0.3，密度7800kg/m3。

SOLID185单元通过8个节点来定义和构造三维固体结构。单元具有超弹性、应力钢化、蠕变、大变形和大应变能力。

3.1.3 边界条件

1）阶梯轴的第二段底端约束所有自由度；

2）阶梯轴的第一段顶端施加1500N·m的周向扭矩载荷，求解应力。

在构件中心部位建立一个中心节点，使用MPC184单元，在中心节点与其他受力节点之间分别建立多根刚性梁单元，形成刚性面。加载荷至中心节点，通过刚性梁来传递载荷，如图2所示。

梁单元使用MPC184单元，在构件中心部位距离阶梯轴10mm的位置建立一个节点（节点与阶梯轴的距离可改变，并不影响扭矩的传递效果），与其他受力节点分别形成多根刚性梁，从而形成刚性面。其他受力节点为断面外圆平均分成30个单元的31个节点。通过命令操作查找出断面外圆节点编号，可知节点编号为连续的，故通过程序命令直接生成所有的刚性梁单元。最后直接将载荷加载至中心节点，通过刚性梁来传递载荷。

图2 传递力矩的刚性梁单元

3.1.4 求解与应力计算

在添加完中心节点上的纯扭转载荷和断面上的全约束后，通过ANSYS的求解模块进行求解，通用后处理模块显示出三维实体的应力分布云图和应变分布云图，以及von-mises等效应力、应变分布图。如图3所示，可观察到应力集中现象出现。

图3 阶梯轴von-mises等效应力分布(D=30，d=15，r=2.0)

3.2 过渡圆角半径对圆轴应力的影响

3.2.1 过渡圆角对应力的影响

通过过渡圆角半径以及阶梯轴最小半径不同圆轴进行计算，得出不同圆角半径和最小轴径组合产生的最大应力值，见表1。圆轴的最大应力随着过渡圆角半径的变化如图4所示。

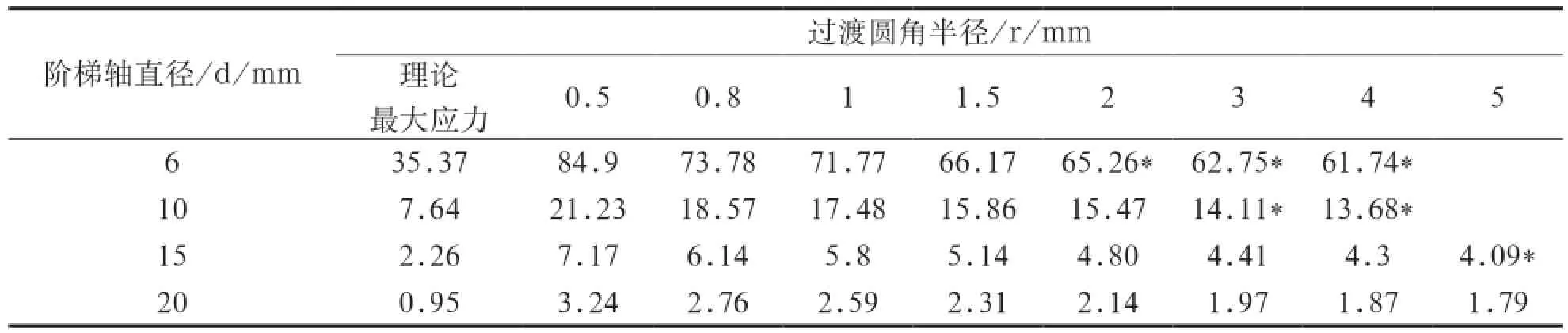
表1 最大应力值σmax/MPa

图4 最大应力与过渡圆角半径的关系

从图4中可以看出阶梯轴最大应力随着过渡圆角的增长而减小。当r=0.5或0.8mm，过渡圆角半径较小时，任何轴径的最大应力值都比过渡圆角半径大，即在过渡圆角较小时应力集中较大。随着过渡圆角半径的增大，同一轴径的最大应力逐渐减小，并在过渡圆角半径增大到一定程度时消失，应力集中现象也逐渐减弱并消失。

3.2.2 过渡圆角半径与轴径的关系及影响

根据过渡圆角增大，应力集中消失的现象针对每个轴径具体分析：由图5显示，过渡圆角半径与轴径的比值，和最大应力的关系可以描述成：当r/d＜0.2时，随着r/d的增大，最大应力处于急剧下降阶段，之后逐渐变缓；当r/d＞0.3时，最大应力的下降趋势已逐渐收敛。从图5（a）、图5（b）、图5（c）中可以看出，当r/d≥0.3时，应力最大处是轴的最小径处，已不存在或者仅存微弱的应力集中。

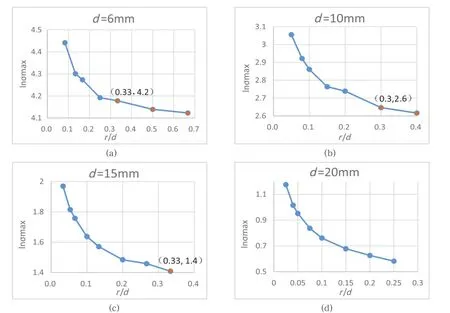
图5 过渡圆角半径与小径关系对最大应力的影响

综上，当过渡圆角半径较小时，阶梯轴根部的最大应力较大，应力集中现象严重，导致阶梯轴的疲劳寿命极大降低，甚至导致零件被直接破坏。当过渡圆角半径变大时，缺口根部的最大应力有所减轻，应力集中现象得到缓解。当过渡圆角半径足够大，应力最大处已不是阶梯轴的圆角过度位置，而是轴的最小径处，已不存在应力集中现象。

根据仿真实验得出：在不影响装配和润滑条件的情况下，阶梯轴设计可以根据阶梯轴小径d的大小来选择过渡圆角半径r，取r＞0.3d。可保证阶梯轴避免出现严重的应力集中现象，从而延长阶梯轴的疲劳寿命。

4 结语

本文阐述了使用有限元方法进行ANSYS分析的基本思路及过程，通过ANSYS软件建立不同直径和过渡圆角半径的阶梯轴三维模型，进行分析计算。计算阶梯轴模型在纯扭转条件下的应力、应变；找出每个阶梯轴的最大应力，及其存在的位置。根据阶梯轴模型的分析计算结果，绘制了最大应力随过渡圆角半径变化的曲线图和随过渡圆角半径与小径比值的变化曲线图，分析了阶梯轴的结构对应力集中程度的影响。根据分析可知：在一定程度上，应力集中程度随着过渡圆角半径增大而减弱；在不影响装配和润滑条件情况下，为了达到减轻应力集中的目的，在采用圆角过渡的阶梯轴设计中，应根据小径的大小选取适当的过渡圆角半径。

[1]李成，郑艳萍，铁瑛.不同荷载作用下圆孔板孔边及孔口附近应力场的仿真分析[J].中国机械工程，2008(1)：99-102.

[2]李兵.ANSYS14有限元分析自学手册[M].北京：人民邮电出版社，2013.

[3]李有堂，于立群.扭转条件下过渡圆角半径及径比对圆轴疲劳寿命的影响[J].兰州理工大学学报，2008(5)：32-35.

Optimal Design of the Transition Radius of the Stepped Shaft of Electric Tools

Wang Haoqi1, Shao Baolin2
( 1.University of Shanghai for Science and Technology, Shanghai 200093, China; 2.Shanghai Jiangnan Changxin Heavy Indistry Co., Ltd., Shanghai 201913, China )

Based on the ANSYS software, the 3D model of the stepped shaft with different diameters and transition radius was established, and then the stress and strain of the stepped shaft model under pure torsion are calculated. According to the calculated results, both the curves of the maximum stress with the change of the fillet radius and the curve of the change of the fillet radius with the inferior arc are drawn, while the analysis of the influence of stepped shaft structure on stress concentration is given.

Stepped shaft; Stress concentration; Finite element; Transition fillet

TM02

A

1674-2796（2017）01-0001-04

2016-10-18

王浩琦（1993-），男，大学本科，主要从事产品优化设计等方向研究。