一种新的被控混沌系统抗干扰控制器设计方法

王 颀，王银河

(广东工业大学 自动化学院，广州 510006)

一种新的被控混沌系统抗干扰控制器设计方法

王 颀，王银河

(广东工业大学 自动化学院，广州 510006)

针对一类动态混沌系统，在干扰幅值增大而影响被控混沌系统镇定的情况下，提出了一种利用补偿控制系统(敏感系统)抑制干扰幅值影响的控制设计方法. 这种方法首先将该敏感系统与原被控混沌闭环系统互联，然后通过设计敏感系统的自适应状态反馈控制器，以保证被控混沌闭环系统在干扰幅值增加的情况下仍能够渐近保持原有的稳定性；最后，通过仿真实例进一步验证了文章结论的有效性。

混沌系统; 渐近稳定; 干扰幅值抑制

0 引言

在控制理论研究领域，混沌作为非线性动态系统的一种状态行为表现，其特性与控制策略已经在诸如生物、经济、通讯等领域中得到广泛应用[1-3]。一方面混沌自身所具有的伪随机特性与同步控制相结合可以产生信号保密传输的方法[4]，另一方面，混沌的非线性特性往往会导致被控系统失稳，因此在一些工程应用中，镇定混沌系统成为首要任务，其中利用状态反馈方法镇定混沌系统是一种常用的方法[1,5-8]。值得注意的是，系统运行过程中往往还会受各种干扰的影响，干扰强度的增加也会导致闭环系统失稳，例如，一个稳定的闭环网络在受到外界干扰时会失去稳定[9]；磁悬浮列车在转弯时，受到各种载荷干扰严重时同样会导致系统的失稳[10]；文献[11-12]也讨论了稳定的系统在受到外界干扰时会失去稳定。因此，如何设计一种能够抑制干扰的控制器以保证闭环系统稳定运行是一个值得研究的问题。

干扰抑制是控制理论中的基础问题，该问题是1976年首先由Francis和Wonham针对线性系统提出[13]。随后，干扰抑制问题扩展到了非线性系统的情形[14-17]。这些研究都假定了干扰源遵循某种已知的动态方程。但是，在实际工程中，确定干扰源的动态方程往往是比较困难的，因此，在干扰源动态方程未知的情况下如何设计一种能够抑制干扰的控制器以保证闭环系统稳定运行是完全必要的。

本文针对一类动态混沌系统，在干扰频率不变而幅值增加的情形下，在原有线性反馈稳定控制的基础上，提出一种新的干扰抑制控制方法，其特点在于当被控闭环系统受到外界干扰幅值增大而失去稳定时，通过将一个带有控制的敏感系统与原系统互联的方式，使闭环系统重新恢复稳定。

本文的安排如下：第一节中，我们给出了一类混沌系统的动态方程以及线性反馈稳定控制器的表达形式，提出在外界干扰幅值增大的作用下，闭环混沌系统失稳的问题。第二节中，我们给出了敏感系统的动态方程形式以及它与被控混沌系统的连接方式。第三节中，在一些假设条件下给出了干扰抑制控制器的形式，并严格证明了在外界干扰幅值增大时，敏感系统与被控混沌系统构成的互联闭环混沌系统保证了被控混沌系统的稳定性。最后，第四节我们通过一个例子来验证该方法的有效性。

1 提出问题

考虑如下形式的混沌系统：

(1)

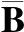
注意到混沌系统(1)可视为一类非线性系统，因此，镇定混沌系统是稳定性理论研究中的首要任务，其中，利用状态反馈控制器镇定混沌系统是常用的方法之一。为此，混沌系统(1)可以改写为如下形式：

(2)

其中：uk∈Rq为控制输入，Bk∈Rn×q为已知的控制增益矩阵。

在状态反馈控制器中，线性反馈控制器不仅简单而且易于物理实现，因此本文采用如下线性控制器uk：

uk=Kx

(3)

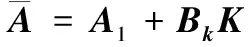
由系统(2)与控制器(3)形成的闭环系统为：

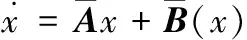
(4)

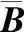
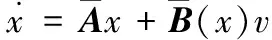
(5)

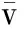
2 系统模型描述与敏感系统设计

考虑如下形式的敏感系统：

(6)

其中：状态向量ω∈W⊆Rm，W有界闭集；v=v(t)∈R是连续的有界干扰；A∈Rm×m是Hurwitz矩阵，B∈Rm是实矩阵；r=(r1r2…rm)T∈Rm是设计常向量；us∈Rm是敏感系统的控制输入。

将敏感系统(6)与系统(5)互联形成如下组合系统：

(7a)

(7b)

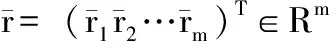
为叙述方便起见，系统(7b)称为目标系统，系统(7a)称为系统(7b)的敏感系统。

为了方便叙述，将组合系统(7)在干扰由v变为pv前后的动态模型统一表示为：

(8a)

(8b)

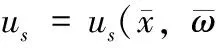
3 敏感系统控制器设计

引入下列误差量：

(9a)

(9b)

将(9a)和(9b)两边分别对时间求导，利用(8)式可得：

(10a)

(10b)

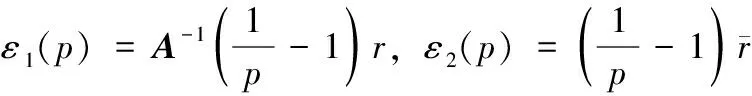
(11a)

(11b)

(11c)

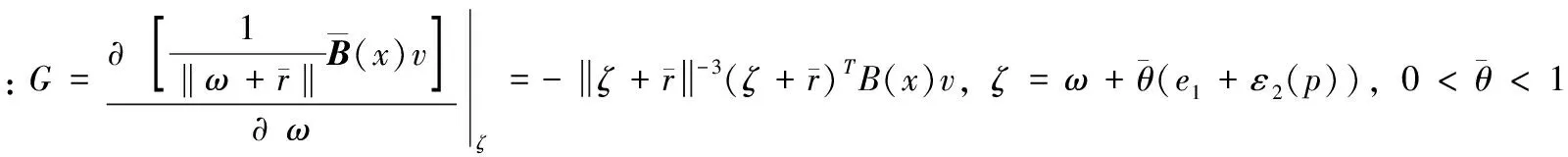
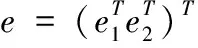
(12)

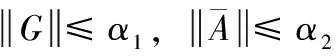
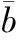
假设4:(i)对于(8)式中所描述的动态系统，n≤m，即敏感系统的维数不小于目标系统的维数; (ii)存在两个正定矩阵Qi、一个n×m的行满秩矩阵Γ以及正数λi,μi,i=1,2，满足下式：

(13a)

(13b)

(13c)

(13d)

其中:Ii,i=1,2是维数匹配的单位阵;S≤0(S>0)表示矩阵S是负半定(正定)的；λmin(*)表示矩阵*最小的特征值；

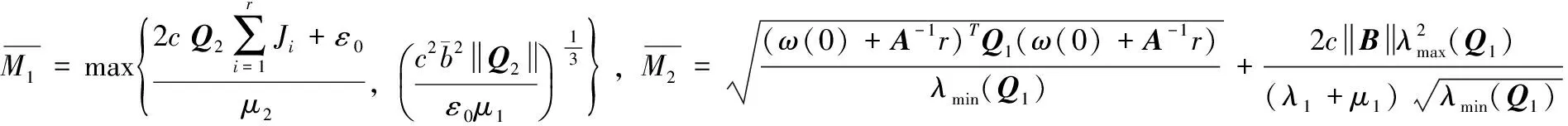
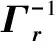
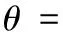
(14)

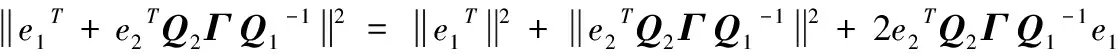
(15)

定义1:设Θ为一列向量，定义如下向量函数Sign(Θ)：

(16)

通过上述定义1，可以知道ΘTSign(Θ)=Θ。当p≠1，利用定义1中的函数，可以设计(8)式中的us：

us=

(17a)

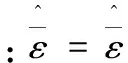
(17b)

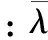
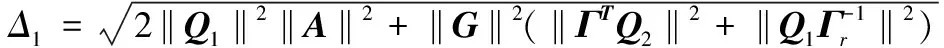
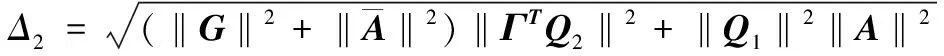
定理1:考虑动态方程(8)。如果假设1-假设4成立，那么在带有自适应律(17b)的控制器(17a)的作用下有下式成立：

(18a)

(18b)

证明：考虑闭环系统(12)，式中us(t)的值如(17)式中所示。

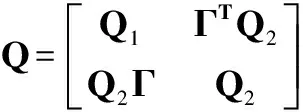
(19)

假设4:意味着下式成立：

(20)

将(20)式代入(19)中，可得：

(21a)

如果θ≠0，联立(15)、(21a)以及(17a)和(17b)，可得：

(21b)

如果θ=0，由(15)式以及(17a)、(17b)式，显然可得：

(21c)

注1： 利用定理1解决混沌闭环稳定系统(4)的受扰系统(5)渐近恢复稳定的步骤如下：

步骤1：构造敏感系统(6)，并将其与系统(5)互联形成组合系统(7)；

步骤2：验证假定1-4，若假定1-4成立则进行下一步，否则本文方法失效；

步骤4：构造带有自适应律(17b)的控制器(17a)。

4 仿真实例

考虑如下Lorentz混沌系统[22]：

(22)

其中：

图1 Lorentz混沌系统相位图

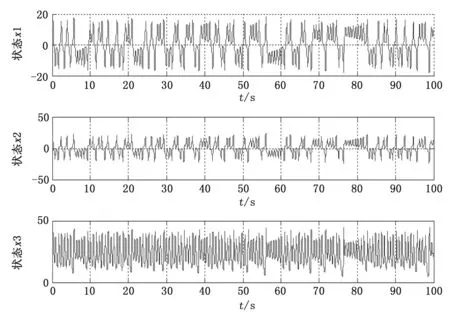
图2 Lorentz混沌系统状态时间响应图

为Lorentz混沌系统(22)设计线性状态反馈控制器uk：

uk=Akx

(23)

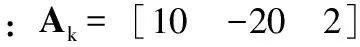
控制器(23)与Lorentz混沌系统(22)形成的闭环系统为：

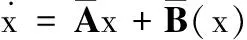
(24)

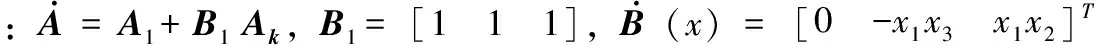
线性状态反馈控制器(23)保证了闭环系统(24)的稳定性，如图3所示。

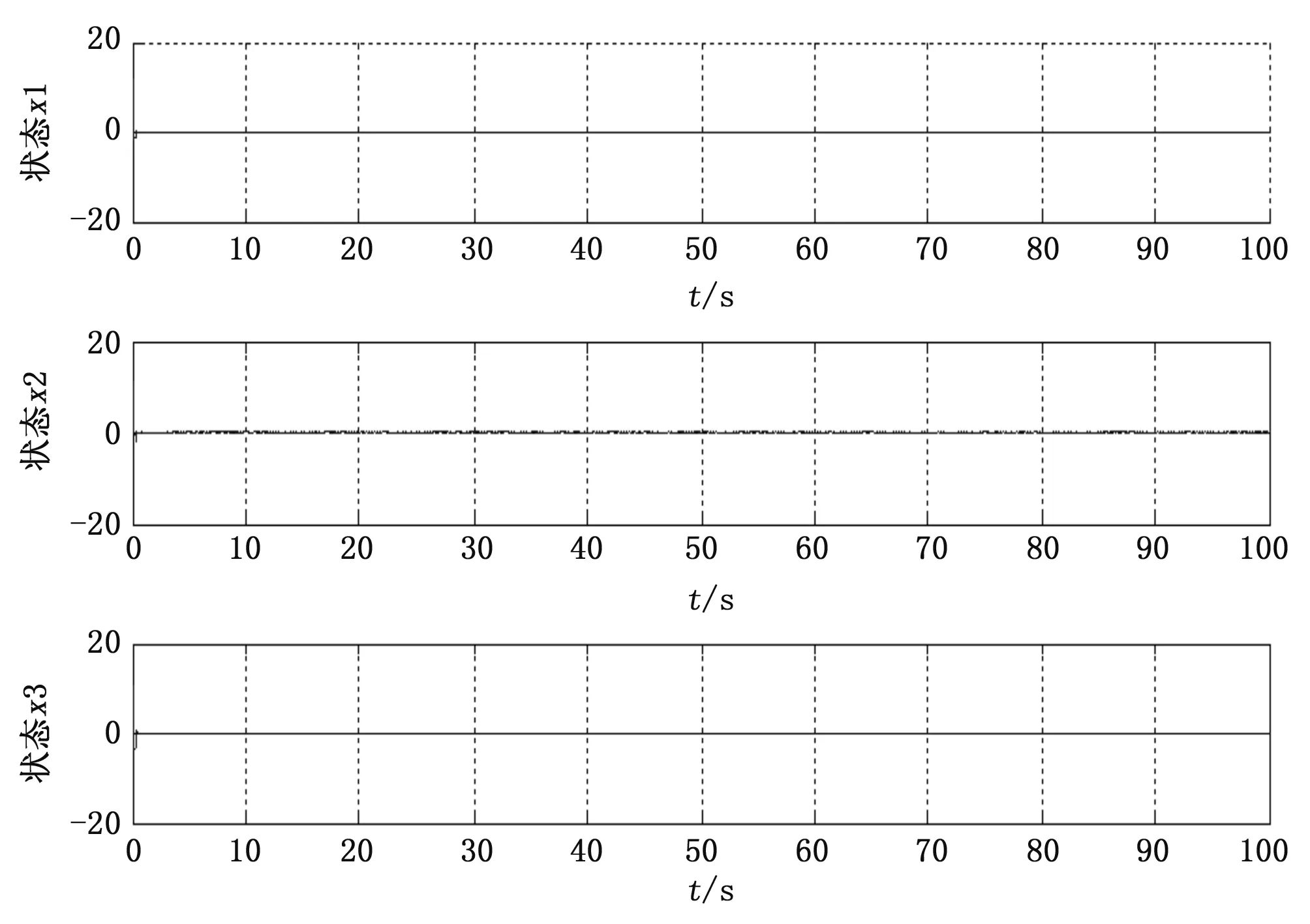
图3 线性状态反馈控制器(23)作用下闭环系统状态时间响应

上图表明在线性状态反馈控制器(23)的作用下，可以使闭环系统稳定。但是在闭环系统(24)受到外界干扰v=p[|sin(100t)|+1]作用时，若幅值p过大会导致失稳，如图4(p=400)。

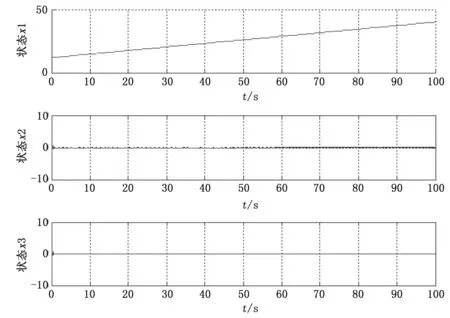
图4 闭环系统(24)受大幅值p=400干扰时的状态时间响应曲线

图4表明，当闭环系统(24)受到的干扰幅值增大到一定程度后，线性状态反馈控制器(23)不能镇定混沌系统。此时，为了使闭环系统(24)依然保持稳定，考虑形如(6)的敏感系统，将其与闭环系统(24)互联形成如下组合系统：

(26a)

(26b)

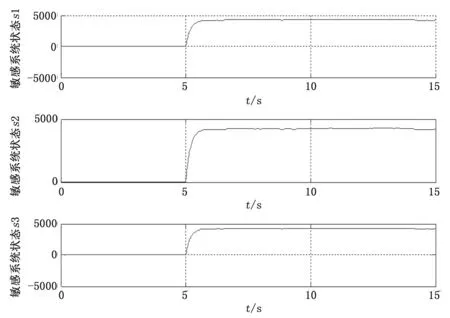
图5 p=400时敏感系统(26a)状态响应

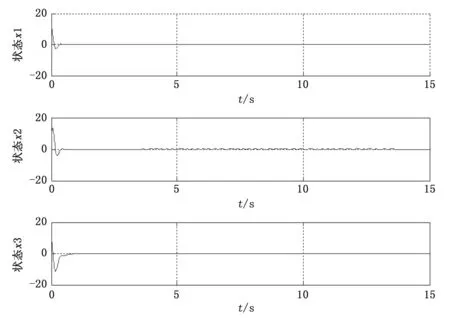
图6 p=400时目标系统(26b)的状态响应

图5表明，当混沌闭环系统(24)受到的干扰幅值在t=5时从p=1突变到p=400，控制器up(t)能够使闭环系统渐近恢复稳定。

5 结论

本文针对一类混沌系统，提出了一种能够抑制干扰幅值变化而恢复稳定的控制策略。当混沌系统不受干扰时，可以使用极点配置方法和非线性系统近似线性化方法设计线性状态反馈控制器使其镇定。一般情况下，当镇定系统受到幅值较小的干扰时，仅仅依靠线性控制器仍然可以保持系统的稳定。但是，当干扰的幅值增大时，线性状态反馈控制器不能使系统保持稳定。在这种情况下，引入一个带有控制器的敏感系统与原系统互联，构成一个组合系统，使得当原镇定系统遭遇较大幅值的干扰时仍然能够保证其渐近恢复稳定。

[1] 张 悦, 张庆灵. 基于广义生物经济系统的混沌控制[J]. 控制与决策, 2007, 22(4): 445-452.

[2] 关新平, 范正平, 陈彩莲. 混沌控制及其在保密通讯中的应用[M]. 北京: 国防工业出版社, 2002.

[3] 黄小原. 动态经济系统中的混沌[J]. 系统工程, 1990, 8(1): 49-54.

[4]KinzelW.,EnglertA.,KanterI.Onchaossynchronizationandsecurecommunication[J].PhilosophicalTransactionsoftheRoyalSocietyA, 2010, 368(1911): 379-389.

[5] 陈立群, 刘延柱. 用精确线性化控制Lorenz混沌[J]. 应用数学和力学, 1998, 19(1): 63-69.

[6] 李瑞红, 徐 伟, 李 爽. 一类新混沌系统的线性状态反馈控制[J]. 物理学报, 2006,(55)2: 598-604.

[7] 朱志宇. 基于反馈精确线性化的混沌系统同步控制方法[J]. 物理学报, 2005,(55)12: 6248-6252.

[8] 孙常春, 方 勃, 黄文虎. 基于线性状态反馈的混沌系统全局控制[J]. 物理学报, 2011, 60(11): 110503.

[9]DingZT.AsymptoticRejectionofGeneralPeriodicDisturbancesinOutput-feedbackNonlinearSystems[J].IEEETransactionsonAutomaticControl, 2006,51(2): 303-308.

[10] 雷思清. 考虑轨道竖曲线引起的载荷干扰的悬浮控制技术研究[D].长沙: 国防科技大学, 2011.

[11] 殷晨波, 周庆敏, 徐海涵, 杨敏. 拟人机器人抗干扰行走稳定性分析[J]. 控制与决策, 2006, 21(6): 619-624.

[12]WangP,LiuLH,WuJ,etal.Reentryvehiclemodelingandslidingmodecontrollerdesign[A].Proceedingsofthe5thInternationalConferenceonRecentAdvancesinSpaceTechnologies[C]. 2011: 227-231.

[13]HuangJ.AsymptoticTrackingandDisturbanceRejectioninUncertainNonlinearSystem[J].IEEETransactionsonAutomaticControl, 1995, 40(6): 1118-1122.

[14] 徐晓惠, 张继业, 施继忠, 等. 脉冲干扰时滞复值神经网络的稳定性分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 166-170.

[15]DelliPriscoliF,MarconiL,LsidoriA.ANewApproachtoAdaptiveNonlinearRegulation[J].SIAMJournalonControlandOptimization, 2006, 45(3): 829-855.

[16]AlbertoIsidori,LorenzoMarconi,LaurentPraly.Robustdesignofnonlinearinternalmodelswithoutadaptation[J].Automatica, 2012, 48(10): 2409-2419.

[17]DongYi,HuangJie.CooperativeGlobalOutputRegulationforaClassofNonlinearMulti-AgentSystems[J].IEEETransactionsonAutomaticControl, 2014, 59(5): 1348-1354.

[18] 黄丽莲, 齐 雪. 基于自适应滑模控制的不同维分数阶混沌系统的同步[J]. 物理学报, 2013, 62(8):080507.

[19] 陈帝伊, 申 滔, 马孝义. 参数不定的旋转圆盘在有界扰动下混沌振动的滑模变结构控制[J]. 物理学报, 2011, 60(5): 050505.

[20] 刘 蕾, 张国山. 基于动态补偿的线性系统最优干扰抑制[J]. 控制理论与应用, 2013, 30(7): 808-814.

[21]DouglasE.Crabtree,EmilieV.Haynsworth.AnidentityfortheSchurcomplementofamatrix[J].proc, 1969, 22(2): 364-366.

[22]JamesH.Curry.AgeneralizedLorenzsystem[J].CommunicationsinMathematicalPhysics, 1978, 60(3): 193-204.

A New Disturbance Rejection Control Scheme for a Class of Controlled Dynamic Chaotic Systems

Wang Qi，Wang Yinhe

(School of Automation, Guangdong University of Technology, Guangzhou 510006,China)

By employing the compensation system (sensitive system), the control scheme for disturbance amplitude rejection is proposed in this paper for a class of controlled dynamic chaotic systems in the case of disturbance amplitude increase. The control design first interconnects the controlled dynamic chaotic system with the sensitive system to form the interconnection system, then the adaptive state feedback controller is synthesized for the sensitive system to asymptotically guarantee the original stability of the controlled dynamic chaotic systems with disturbance amplitude increase. Finally, the demonstration of effectiveness is given in this paper by simulation example.

chaotic systems; asymptotical stability; disturbance amplitude rejection

2016-07-30；

2016-09-06。

王 颀(1993-),男,山西长治人,硕士,主要从事非线性系统控制方面的研究。

王银河(1962-),男,内蒙古包头人,教授,博士生导师,主要从事非线性控制系统鲁棒自适应控制设计、复杂网络等方向的研究。

1671-4598(2017)01-0076-06

10.16526/j.cnki.11-4762/tp.2017.01.022

TK323

A