研究型与实验型相结合的离散数学教学模式
2017-02-25郑红波秦绪佳
郑红波,秦绪佳
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310032)
研究型与实验型相结合的离散数学教学模式
郑红波,秦绪佳
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310032)
针对离散数学课程的教学现状及存在问题,提出在离散数学的教学中引入研究型和实验型相结合的教学模式。分析和设计研究型与实验型的教学模式和题库,阐述研究型项目和实验型项目的具体实施,培养学生研究问题、分析问题和解决问题的能力。
研究型与实验型;离散数学;计算思维;教学模式
1 离散数学的教学现状
离散数学以形式化、抽象的方法分析问题,研究离散量结构及相互关系,是计算机科学与技术专业的核心课程和理论基础课程,对培养学生抽象思维能力和逻辑推理能力、培养学生数学建模能力和解决实际问题的能力起着重要的作用[14],这些能力的培养正是计算思维的具体体现和很好的诠释[5]。拥有计算思维能力、具备运用计算机概念和知识解决工程问题的能力,也是中国工程教育计算机专业认证的产出要求和细化标准。离散数学课程为培养学生的计算思维能力提供了一个很好的教学平台。然而,笔者作为离散数学课程一线授课教师,通过多年的教学实践,发现目前离散数学教学还存在以下问题[14]。
1)知识单元涵盖的难点多,概念抽象生涩,知识难于理解和应用。
离散数学课程概念多、理论性强、高度抽象,是计算机学科的专业基础课,在很多后续专业课程中有广泛的应用。然而在学习这门课程的时候,大部分专业课程还未开课,学生对离散数学的应用没有直观感受,影响了学习兴趣,这使学生在学习中感觉内容脱离应用、抽象难理解,影响了学习的积极性。
2)课程偏重理论叙述和定理证明,忽视实验性教学环节。
离散数学的教学过程忽视实验教学环节,学生在学习过程中无法体会离散数学的重要作用,不能充分体现专业基础课的实用性,难以调动学生的学习主动性和积极性,影响了创新意识与创新能力的培养。
3)学生的计算机科学问题求解能力方面存在不足。
随着计算机科学技术的发展,能够正确理解计算机学科的基础概念,能够灵活运用各种思想、方法和技术解决实际问题,将成为未来计算机专业人才的必备技能。这些技能正是计算思维培养的目标。但当前的课程教材缺乏培养学生计算思维能力的体系建设,学生的计算机科学问题求解能力方面存在不足。
作为计算机核心课程中最具基础性和理论性的课程,离散数学的教学问题会影响学生的学习和培养,改革势在必行。因此,在离散数学的教学中引人“研究型和实验型相结合的教学模式”,加强培养学生的研究问题、分析问题、解决问题?的能力,加强培养学生的动手能力和专业技能,就成为课程教学中重要而迫切的任务。
2 研究型与实验型相结合的教学模式改革
应采用研究型教学,了解课程中内容的应用领域、相关知识,培养学生的独立探索能力,提高学生的兴趣,让学生在学习中感受到学有所用;设计实验,提高学生的动手能力和解决问题能力,让学生对离散课程知识点有更深人的理解。本改革的理念是:基于培养计算思维能力的产出要求[5],优化离散数学课程的教学内容和方式,增强离散数学的研究型教学和实验性教学,突出离散数学的应用,加强学生实践的锻炼,旨在提升其以问题分析能力、程序设计能力和基础创新及工程实践能力为标志的计算思维能力,使学生通过课程的学习和锻炼提升实践能力的培养。
教学过程中,教师要注重启发引导学生,将以往被动式教学模式改变为以学生为主体的教学模式;激励学生积极思考问题,探讨未知知识,研究知识的应用,营造双向、互动的教学氛围;加强对学生理论联系实际、实践动手能力和创新精神的培养;采用多层次教学方式,因材施教,使各层次的学生获得更多的知识和锻炼。
3 研究型与实验型相结合的教学模式设计
3.1 研究型教学设计
一般的离散数学课程分两个学期开展,分别为离散数学Ⅰ和离散数学Ⅱ。离散数学Ⅰ的教学内容为数理逻辑、集合与关系、函数,离散数学Ⅱ的教学内容为代数系统、图论[4]。每个学期每个学生需要参加一个研究型项目和一个实验型项目。
布置课前阅读题目,让学生了解与课程内容相关的背景知识、前沿知识和应用实例;也可为一些知识点设计课后研究型题目,让学生通过查阅资料、撰写学习报告来加深对新概念的理解,同时尝试用所学理论和方法解决实际问题。在研究型教学设计中,选择哪些主题和项目是设计的难点。学生没有学过离散数学的应用知识,看不懂或不太理解太难太深奥的知识或应用。因此,在设计研究型主题时,可以采用教师布置规定和学生自主设计两种方式。笔者在离散数学Ⅰ部分设计了逻辑和关系的相关应用,在离散数学Ⅱ部分设计了图论的应用,见表1。

表1 离散数学研究型项目表
对于这些研究型的知识和实例,教师可以布置为学生小组、团队研究项目,也可以要求学生自己探索感兴趣的项目或有疑问的内容,培养学生发现问题、探索问题的能力,强化学生的自主学习能力和独立钻研能力。课前十分钟可以让学生讲解、讨论和分析这些研究型的项目,也可以集中到学期末进行研讨并提交研究报告。
3.2 实验型教学设计
实行以应用为主体、多层次的实验教学模式,开设实验和课程设计是加强实践性教学的重要手段。由教师设计好实验题目要求,然后布置给学生去实现。实验设计要考虑学生的编程能力和先修课程,一般以小组、团队的形式课外进行。离散数学一般在大一开课,和学生的程序设计课程同步进行,学生的编程能力有限,因此设计的实验以基础实验为主。笔者在离散数学Ⅰ部分设计了集合与关系方面的实验内容,在离散数学Ⅱ部分设计了群的综合实验,如表2所示。

表2 离散数学实验型项目表
4 研究型与实验型相结合的教学实施示例
4.1 研究型项目教学
逻辑应用到生活中的例子很多,可以让学生自行查找资料,然后分析讨论结果。我们利用课前十分钟让学生讲解、讨论和总结,分析用到的命题及其逻辑定律,分析与教学内容的衔接,培养学生发现问题、探索问题的能力,强化学生的自主学习能力和独立钻研能力,提高学生的学习兴趣和动力。以下是学生探究的一个案例。
盖亚、瑞亚、赫拉和雅典娜是古希腊少女,她们正在接受训练以便当一个预言家。实际上,只有一个人成了预言家,并在特尔斐城谋得一个职位,其余3个人,一个当了职业舞蹈家,一个当了宫廷女侍,一个当了演奏家。一天,她们在练习讲预言。
盖亚预言:“瑞亚无论如何也成不了职业舞蹈家。”
瑞亚预言:“赫拉将成为特尔斐城的预言家。”
赫拉预言:“雅典娜不会成为演奏家。”
雅典娜预言:“我自己将嫁给一个叫阿特的男人。”
事实上她们只有一个人的预言是正确的,而正是这个人当了特尔斐城的预言家。
请用逻辑解之:她们四个人中谁当了什么?雅典娜和阿特结婚了吗?
解题思路:将简单命题符号化。
A:盖亚是预言家 。
B:瑞亚是预言家。
C:赫拉是预言家 。
D:雅典娜是预言家。
只有一个人的预言正确且只有一人是预言家,所以A、B、C、D只有一个为真。若B为真,则C也为真,这与只有一人是预言家的前提相矛盾,所以B为假。因为B为假,所以瑞亚的预言为假,则赫拉不是预言家,即C为假,那么赫拉的预言也是错的,即“雅典娜不会成为演奏家”是假的。根据双重否定定律,则“雅典娜是演奏家”是真的。既然雅典娜是演奏家,那么D为假,则雅典娜不会和阿特结婚。
由此可知,命题B、C、D为假,只有命题A为真,即盖亚是预言家。因此盖亚的预言为真,瑞亚不是职业舞蹈家。根据事实的排他性,瑞亚是宫廷女侍,赫拉是职业舞蹈家。综上,盖亚是预言家,瑞亚是宫廷女侍,赫拉是职业舞蹈家,雅典娜是演奏家,且雅典娜没有和阿特结婚。
4.2 实验型项目教学
实验项目一般采取团队、小组的形式在课外进行,安排学生在学期末进行实验演示、报告、答辩。课程最后,学生要递交实验报告,报告中写明实验目的、内容、编程思想、重要代码段及其分析、实验结果等,最好在报告中说明小组成员的工作分配。教师可以根据实验的难易程度分析实验型项目,如果项目比较简单(如集合的运算),就不用分析,让学生自己实现;如果项目较难(如代数系统的群),教师可以帮助学生分析系统及其数据。根据群的数学定义,假定输人n个有限的元素集合G,G中有运算*,不同的元素通过运算*产生不同的结果,运算结果构成一个n*n的二维运算表,通过检查运算表中的元素,判断此代数系统是否为群。因为此时大部分学生没学过C++的单文档和多文档,数据输人需要采用控制台程序的键盘输人,输出可以用二维数组表示,输人后判定此代数系统的性质。要判定代数系统性质,先要判定封闭性、结合律、有幺元、每个元素有逆元,可以编写几个函数进行判定,如isClosure函数(用来判断是否封闭)、isAssociativity函数(用来判断是否具有结合性)、isExchange函数(用来判断是否具有交换律)、ifIdentityElement函数(用来判断是否含有幺元)、isEveryInverseElement函数(含有幺元时,是否每个元素都存在逆元)等。具体的函数实现,课程中已经讲得比较清楚,学生自行实现即可,图1是一组学生实验的结果。
5 结 语
通过研究型与实验型相结合的教学模式,大大提高了学生参与研究、讨论、主动思考和实践项目执行在课程中的比重,学生的主动性与创新实践能力大大加强,提高了学生分析问题和解决问题的能力。该教学模式要求教师对研究项目和实验项目有较多研究,并投人大量的时间和精力,才能使离散课程改革落到实处,真正惠及广大学生。
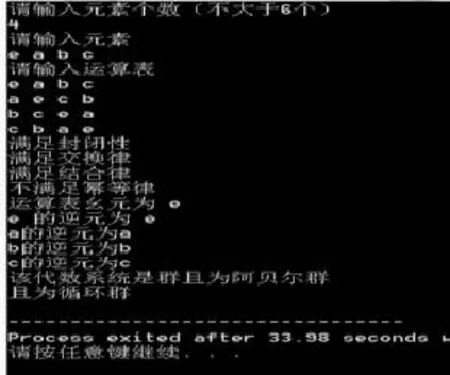
图1 代数系统的实验
[1] 陈光喜, 古天龙.“离散数学”精品课程教学改革实践[J]. 桂林电子科技大学学报, 2007(4): 300-302.
[2] 常亮, 徐周波, 古天龙.离散数学教学中的计算思维培养[J]. 计算机教育, 2011(14): 90-94.
[3] 路芳. 在离散数学课中引入研究型题目的教学实践[J]. 阴山学刊, 2014(3): 86-88.
[4] 王卫红, 李曲, 郑宇军. 离散数学[M]. 清华大学出版社, 2013: 8.
[5] 王飞跃. 面向计算社会的计算素质培养: 计算思维与计算文化[J]. 工业和信息化教育, 2013(6): 4-9.
(编辑:孙怡铭)
1672-5913(2017)01-0120-04
G642
浙江工业大学校级教学改革精品课程项目(JG201512);浙江工业大学科研启动金项目(119005029)。
郑红波,女,讲师,研究方向为形式化方法、虚拟现实,zhb@zjut.eud.cn。
