《正比例》教学实录与评析

2017-02-24王岩梅

广西教育·A版 2016年12期

关键词：教学实录正比例评析

王岩梅

【摘要】本文根据《正比例》一课的教学实录，分析说明了如何让学生经历“观察数量—发现关联，探索规律—对应观察，计算比值—明确规律，表征关系—揭示概念，字母表征”这一过程。

【关键词】正比例教学实录评析

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2016）12A-0061-03

教学内容：人教版义务教育教科书数学六年级下册P45-46。

教学目标：

1.结合丰富的实例，使学生理解相关联的量，理解正比例的意义，掌握正比例的量的变化规律。

2.让学生能根据正比例的意义，判断两个相关联的量是不是成正比例。

3.让学生认识正比例关系的图象，能根据给出的正比例关系的数据在有坐标系的方格纸上画出图象，会根据其中一个量在图象中找出或估计出另一个量的值：体会数形结合的思想。

教学重难点：

重视概念的理解，强调概念的应用，让学生经历“观察数量—发现关联，探索规律—对应观察，计算比值—明确规律，表征关系—揭示概念，字母表征”这一过程。

教学过程：

一、课前谈话引入

1.“水涨船高”是什么意思？（水位升高，船身也随之浮起。比喻事物随着它所凭借的基础的提高而增长提高。）

【过渡】水的变化引起了船的变化，船与水是相关联的，数学中也存在着相关联的量。

2.女孩0-5岁年龄与体重生长曲线图。你发现了什么？（体重随着年龄的变化而变化，年龄与体重是两种相互依赖的相关联的量）

3.生活中还有哪些这样相关联的量？

（学生交流）

【评析】大量实例证明两种相关联的量在我们现实生活中是广泛存在的。只要是一种量变化，引起另一种量发生变化，那么这两种量就是相关联的量。

看似轻描淡写实则用学生最熟悉的知识，解释“相关联”的含义，并加强了语数知识的联系。其实教学中并没有直接进入典型的正比例关系这样一个话题，但数学与生活息息相关，概念的发生形成过程就是现实模型的直接反映。概念引入得当，就可以紧紧地围绕课题，充分地激发学生的兴趣和学习动机，为学生顺利地掌握概念起到了奠基作用。

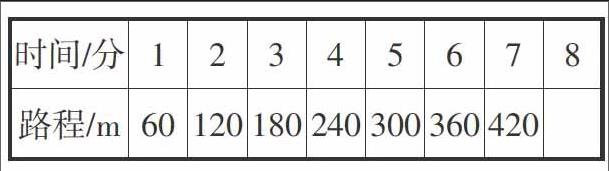
4.小明步行回家的时间和路程如下图。（表一）

师：路程和时间是相关联的两个量吗？8分钟行多少米？

仪仗队通过天安门的时间和路程如下图。（表二）

师：8分钟行多少米？走600米需要多少分钟？

（学生回答）

师：前面两个表都是关于步行时间和路程的统计表。为什么表一不能确定准确地得出与8分钟相对应的路程，而表二通过推算和简单的思考，却能够确定出准确的路程呢？

（学生思考，讨论）

生1：因为仪仗队每分钟走的路程是一样的，而小明每分钟走的路程不一样。

生2：速度不变。

生3：都是60米。

师：你们是怎么看出速度都是60米？

生1：路程÷时间=60。

生2：60[∶]1=120[∶]2=180[∶]3=…=60。

师：原来速度60是隐含的，题目中没有，需要我们动脑筋才能找到。（总结：虽然时间和路程这两种相关联的量是在不断发生着变化，但是，两种量中相对应的数据的比值，也就是他们所步行的速度是保持不变的，在数学上把这个不变的量叫常量或常数，在小学叫一定。这两个变化的量叫变量，小学叫相关联的两个量。根据这个不变的量和其中一个变量就能得到相对应的另一個变量，这就叫“以不变应万变”）

师：小明呢？没有一定的量，也就无法算出8分钟准确的对应量。

【评析】波利亚指出“学习最好的途径是自己去发现”。有些难以理解的概念还可以用对比的方法，化难为易，揭示本质。学生通过对比发现，同样是路程和时间这两个相关联的量，表二的路程和时间有规律——比值一定，而表一的路程和时间没有规律。教师在教学中运用这样的教学方法，不仅使学生掌握了比较法，更重要的是通过长期的训练，使学生的观察、分析、比较、综合等能力有所提高，而能力的提高又会促进和推动学生掌握知识，因此，教师在教学过程中要系统地示范、指导，使学生学会思考，学会学习，真正成为学习的主人。

师：下面请同学们自学P45例1，回答两个问题。

1.完成例1下面三个问题。

2.对比上面两个表，例1与哪个表类似，它们有什么共同点？

二、新知探究

（一）教学正比例意义

出示例1：文具店有一种彩带，销售的情况如下表，你发现了什么？

1.表中有哪两种量？

生：数量和总价。

2.总价是怎样随着数量的变化而变化的？

生1：总价随着数量的变化而变化。

生2：总价随着数量的增大而增大。

生3：数量扩大多少倍总价就扩大多少倍。