族分布下带投资的双险种风险模型中的破产概率
2017-02-24王施施王文胜骆明旭
王施施, 王文胜, 骆明旭
(杭州师范大学理学院,浙江 杭州 310036)
王施施, 王文胜, 骆明旭
(杭州师范大学理学院,浙江 杭州 310036)
1 引言和模型
保险是国民经济的重要组成部分,对整个社会经济的稳定起着至关重要的作用.风险是保险的基础,是衡量保险公司经营能力的一个重要指标.
关于风险理论的研究已有百年历史.1903年,瑞典精算师Filip Lundberg最早开始了保险风险模型的研究,至此经典风险模型被不断研究.众多学者结合实际情况,针对保险公司在运作过程中遇到的种种问题,对经典风险模型进行改进,如对保费收入过程、随机扰动的推广等,大多数考虑的是单一险种风险模型.
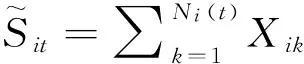
如果假定保险公司拿出一部分盈余投资Black-Scholes型资本市场指数,并假设该指数的价格过程由几何布朗运动驱动,则公司的盈余过程{Ui(t),t≥0}可使用如下随机微分方程描述:
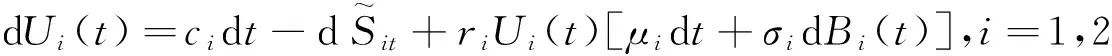
(1)
其中Ui(t)是第i个险种t时刻的盈余,ci是第i个险种的常数保费率,μi>0和σi>0是第i个险种漂移系数和波动率,ri∈[0,1]是公司盈余中用于投资的比例,{Bi(t),t≥0}是标准布朗运动,{Ni(t),i=1,2,t≥0}是第i个险种到t时刻为止保单发生的索赔次数,且{N1(t),t≥0},{N2(t),t≥0}相互独立,{Xik,k=1,2,…,i=1,2},{Bi(t),i=1,2,t≥0},{Ni(t),i=1,2,t≥0}都是相互独立的.
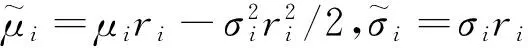
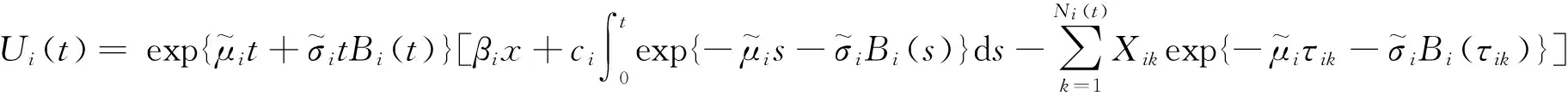
(2)
对于二维风险模型,在有限时间(T>0)内,主要研究以下3种情况下的破产概率.记破产时刻Tmax(x),Tmin(x),Tsum(x)分别为
Tmax(x)=inf{t≥0:max{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},
(3)
Tmin(x)=inf{t≥0:min{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},
(4)
Tsum(x)=inf{t≥0:U1(t)+U2(t)<0|U1(0)=β1x,U2(0)=β2x}.
(5)
则相应的破产概率分别是
Ψmax(x,T)=P(Tmax(x)≤T),
(6)
Ψmin(x,T)=P(Tmin(x)≤T),
(7)
Ψsum(x,T)=P(Tsum(x)≤T).
(8)
2 定义和主要结果
2.1 相关概念
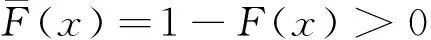
定义1 对随机变量X其分布为F,如果分布F满足:对所有t>0,有
EetX=∞.
(9)
则称随机变量X服从重尾分布.
定义2 对随机变量X其分布为F,如果分布F满足:对任意y>0,都有
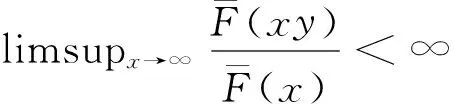
(10)
定义3 对随机变量X其分布为F,如果分布F满足

(11)

令
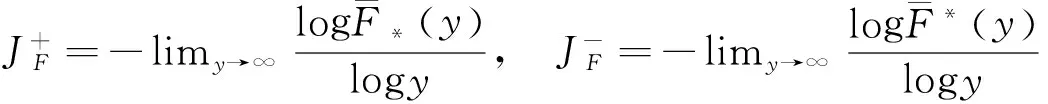
其中
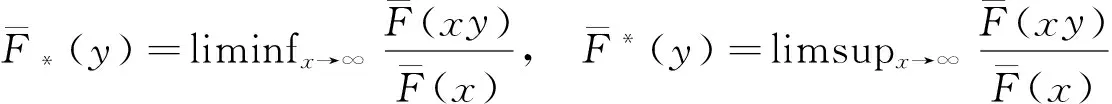
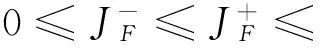
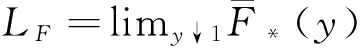

(12)
下面是关于随机变量X之间关系的定义.
定义4 对于两个非负随机变量X1和X2,它们的分布分别为F1和F2,如果满足
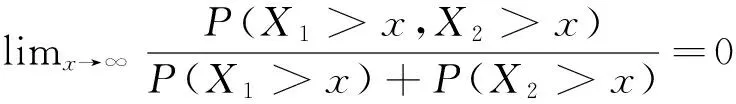
(13)
则X1和X2是拟渐近独立的.
其中下面定理及定理证明中用到的LN(yi;a,b2)表示参数为a和b2的对数正态分布.
2.2 主要结果
Ψmax(x,T).
Ψmax(x,T).
(14)

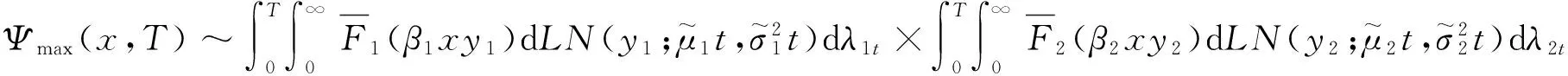
(15)

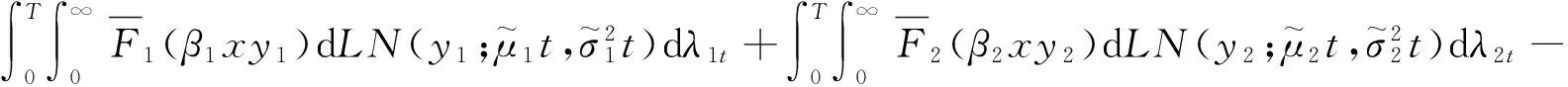
(16)
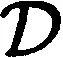
Ψsum(x,T),
Ψsum(x,T).
(17)

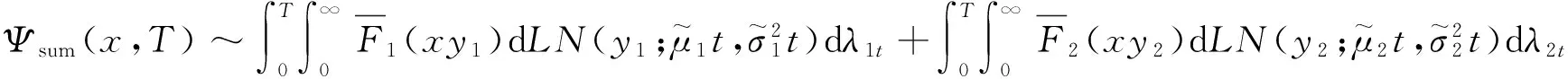
(18)
3 一些引理
引理1 对于[0,∞)上的分布为F的随机变量X有
(1)
(19)
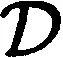
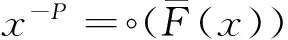
(20)
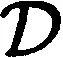
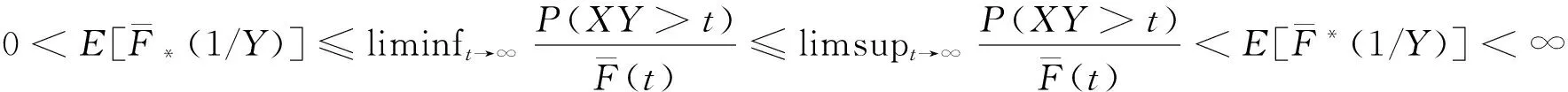
(21)
证明 参见文献[11]中的命题2.2.1,文献[12]中的引理3.5以及文献[13]中的定理3.3.
下面这个引理是关于指数布朗运动积分的一些性质.
引理2 对∀λ∈R,μ∈R以及∀n∈N,有
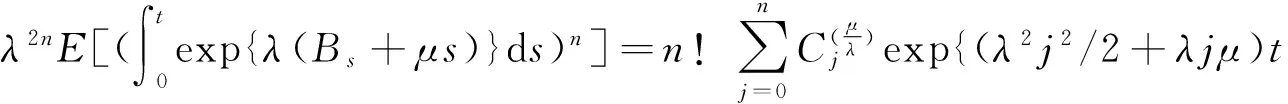
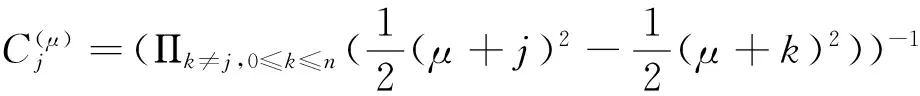
证明 参见文献[14].
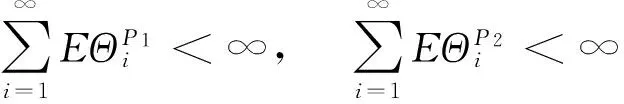
(22)
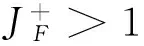
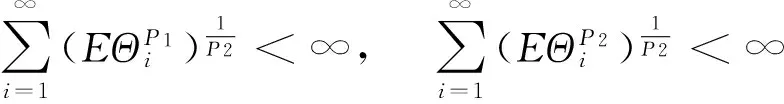
(23)
则有
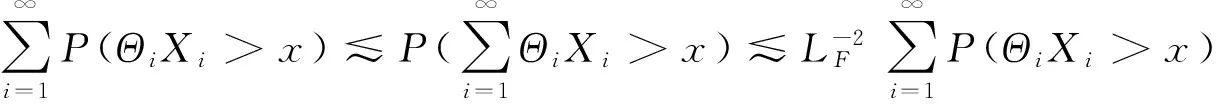
(24)
证明 参见文献[15]中的定理2.
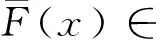
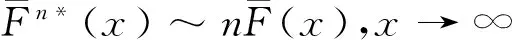
(25)
证明 参见文献[16].
引理5 对于单一险种情形下带投资的风险模型,
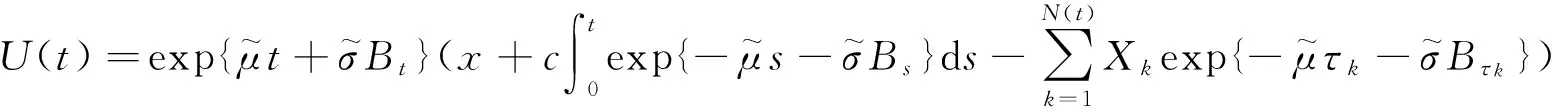
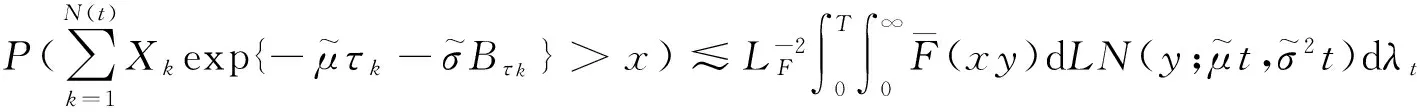
(26)
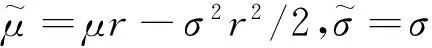
证明 根据Tang[14],可以将该定理的证明和破产概率联系起来,首先令
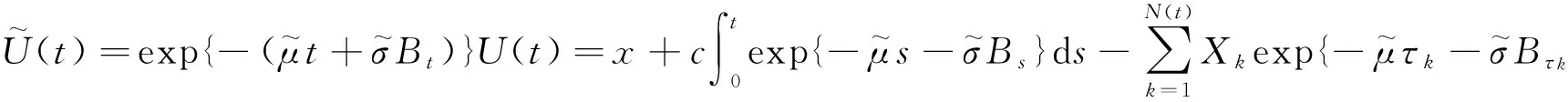
记
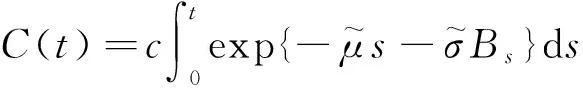
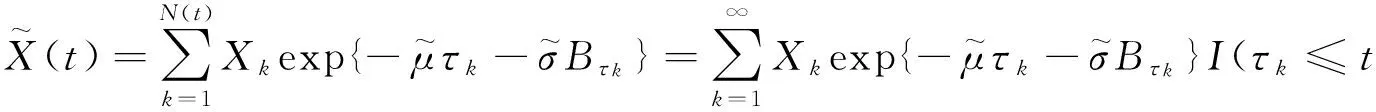
根据更新函数,对∀ρ>0,
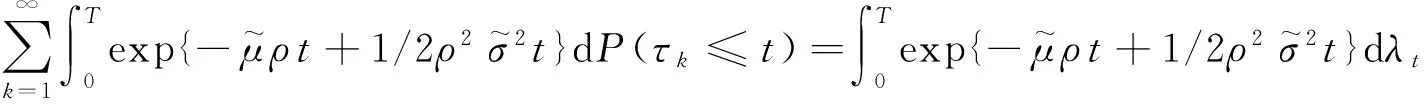
(27)
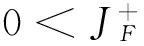
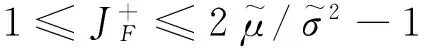

(28)
所以上式说明引理3条件(2)满足.
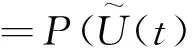
根据引理3得到
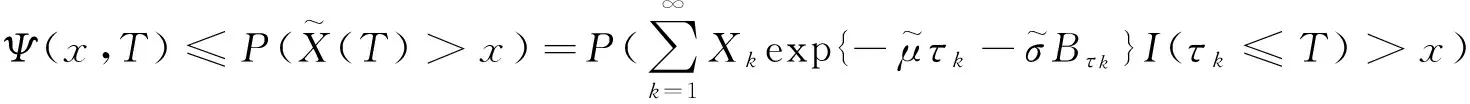
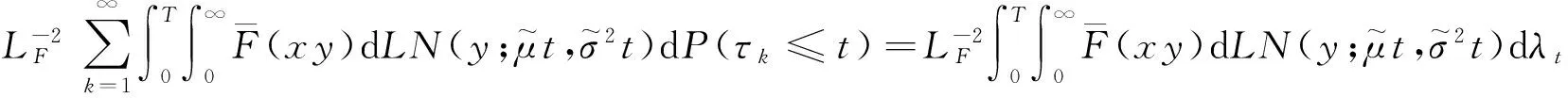
(29)
引理6 对于单一险种情形下带投资的风险模型,
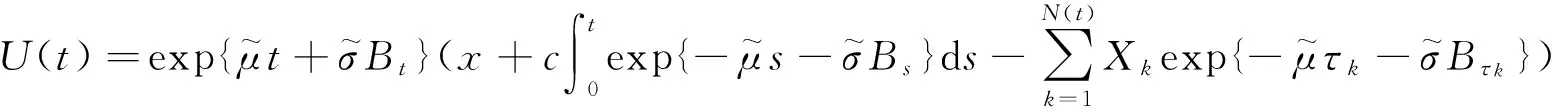
(30)
证明 和引理5证明一样,将此定理证明和破产概率联系起来.由引理5,再根据引理2得到C(T)是一个有界函数.
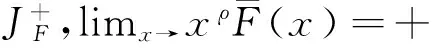

(31)
根据引理3得到
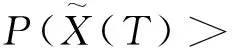
(32)
固定0<ε<1,
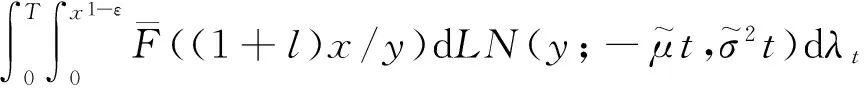
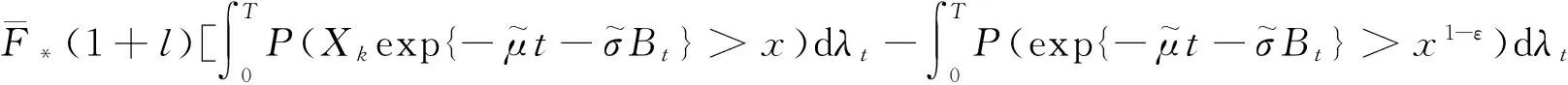
(33)
根据Wei[4]我们可以证明上式第二个积分相对于第一个来说可以忽略.
结合上述及Wei[4]中的结论,由引理1中式(20)得到
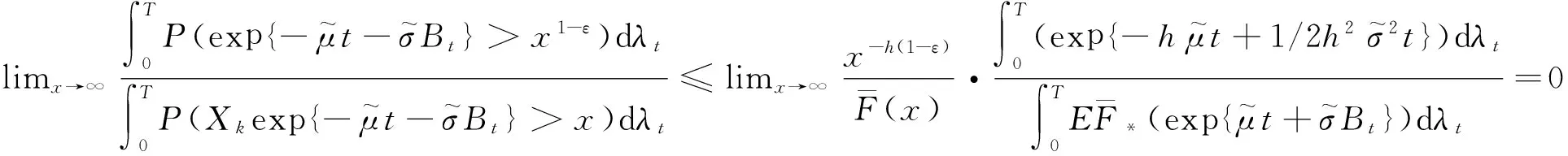
结合式(32)和(33),所以有
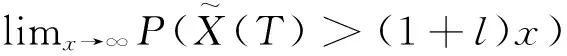

(34)
综上所述得到:
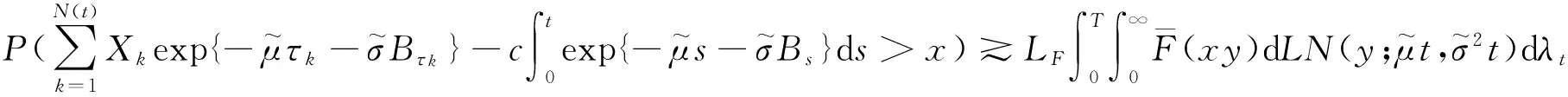
(35)
4 定理的证明
4.1 定理1的证明
首先证明式(3)定义的破产概率的上界,由破产概率Ψmax(x,T)的定义及条件{N1(t),t≥0},{N2(t),t≥0}相互独立,以及{Xik,k=1,2,…},(i=1,2)独立可知
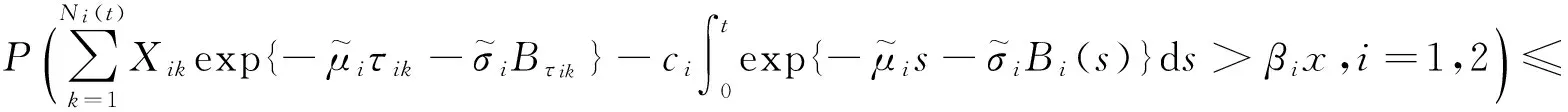
由引理5得
Ψmax(x,T).
(36)
接着要证明破产概率的下界,根据其独立性有
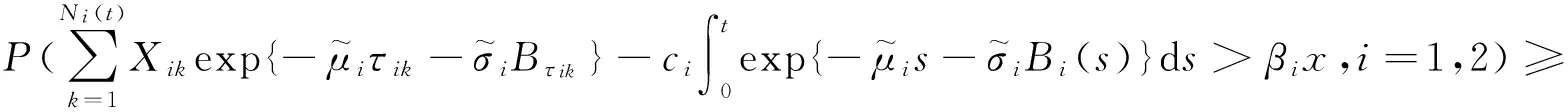
由引理6得
Ψmax(x,T).
(37)
所以定理1的结论就证明了.
4.2 定理2的证明
根据破产概率Ψmin(x,T)的定义及在定理2条件下,令s(xi)=inf{t≥0,Ui(t)<0},则
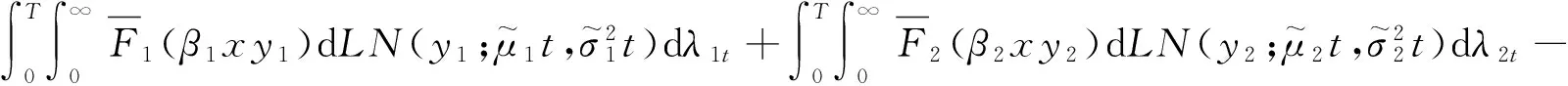
4.3 定理3的证明
定理3的证明和定理1的证明一样,首先考虑式(5)定义的破产概率的上界,由定理3的条件得
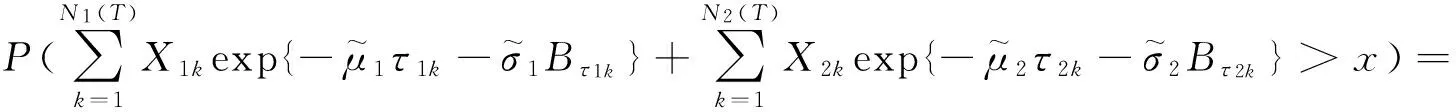
由引理4得
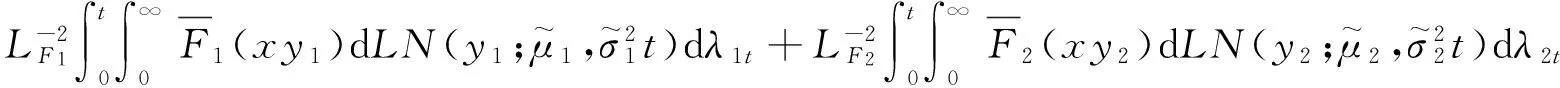
所以
Ψsum(x,T).
(38)
下面考虑破产概率的下界.由式(5)破产概率定义得
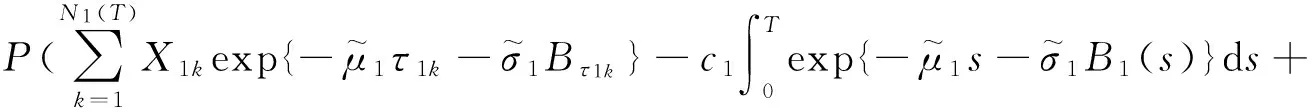
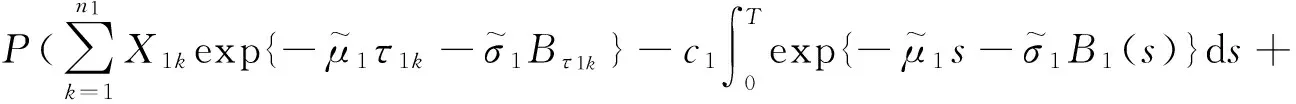
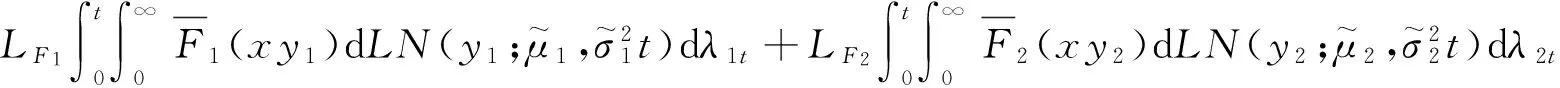
所以

(39)
这样定理3的结论得证.
[1]FROLOVAA,KABANOVY,PERGAMENSHCHIKOVS.Intheinsurancebusinessriskyinvestmentsaredangerous[J].Financestoch,2002,6(2):227-235.
[2]GAIERJ,GRANDITSP.Ruinprobabilitiesandinvestmentunderinterestforceinthepresenceofregularvaryingtails[J].ScandindvianActuarialJournal,2004,4:256-278.
[3]KALASHNIKOVV,NORBERGR.Powertailedruinprobabilitiesinthepresenceofriskyinvestments[J].StochasticProcessandtheirApplications,2002,98(2):211-228.
[4]WEIL.Theruinprobabilityoftherenewalmodelwithriskyinvestmentandlargeclaims[J].SciChinaSerA,2009,39(8):933-938.
[5]WANGG,WUR.Distributionsfortheriskprocesswithastochasticreturnoninvestments[J].StochasticProcessandtheirApplications,2001,95(2):329-341.
[6]AVRAMF,PALMOWSKIZ,PISTORIVSM.Atwo-dimensionalruinproblemonthepositivequardrant[J].Insurance:MathematicsandEconomics,2008,42(1):227-234.
[7]LIJH,LIUZM,TANGQH.Ontheruinprobabilitiesofabidimensionalperturbedriskmodel[J].Insurance:MathematicsandEconomics,2009,41(1):185-195.
[8]DANGLF,ZHUN,ZHANGHM.Survivalprobabilityforatwo-dimensionalriskmodel[J].Insurance:MathematicsandEconomics,2009,44(3):491-496.
[9]ZHANGYY,WANGWS.Ruinprobabilitiesofabidimensionalriskmodelwithinvestment[J].StatistProbabLett,2012,82(1):130-138.
[10]CHENY,HUANGY,ZHANGWP.Asymptoticruinprobabilitiesforproportionalinvestmentunderinterestforcewithdominatedly-varying-tailedclaims[J].JournaloftheKoreanStatisticalSociety,2012,41(1):87-95.
[11]BINGHAMNH,GOLDIECM,TEUGELSJL.Regularvariation[M].Cambridge:CambridgeUniversityPress,1987.
[12]TANGQ,TSITSIASHVILIG.Preciseestimatesfortheruinprobabilityinfinitehorizoninadiscrete-timemodelwithheavy-tailedinsuranceandfinancialrisks[J].StochasticProcessandtheirApplications,2003,108(2):299-325.
[13]CLINEDBH,SAMORODNITSKYG.Subexponentialityoftheproductofindependentrandomvariables[J].StochasticProcessAppl,1994,49(1):75-98.
[14]TANGQ.Asymptoticalruinprobabilitiesoftherenewalmodelwithconstantintrestforceandregularvariation[J].ScandinavianActuarialJournal,2005,3:229-240.
[15]YORM.OnsomeexponentialfunctionalofBrownianmotion[J].AdvancedAppliedProbability,1892,24(3):509-531.
[16]EMBRECHTSP,KLÜPPELBERGC,MIKOSCHT.Modellingextremalevents[M].Berlin,Heidelberg:Springer-Verlag,1997.
Ruin Probabilities of a Two Risk Model with Investment under Dominatedly-varying-tailed Claims
WANG Shishi, WANG Wensheng, LUO Mingxu
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
ruin probability; quasi-independence;dominatedly-varying-tailed class; consistently-varying-tailed class; two-dimensional risk model
2016-04-10
王文胜(1972—),男,教授,主要从事随机过程、金融数学研究. E-mail: wswang@aliyun.com
10.3969/j.issn.1674-232X.2017.01.021
O211.9 MSC2010: 62P20
A
1674-232X(2017)01-0094-09
