让“画图”成为一种习惯

卢珍珍

【摘要】 《长方体和正方体》这一单元内容，是学生学习几何知识由平面扩展到立体的开始，由于学生年龄小，空间想象能力不足，常会对数学问题认识模糊、思路不清。因此在教学中，要多引导学生将数学题以自己喜欢的形式画下来， 让学生在“画”中学，在“画“中悟，把原本枯燥的数学变得直观形象，简便易懂，让学生由怕数学变成爱数学。

【关键词】 画图 数学课堂 应用 意识 策略

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2016）12-027-01

0

学习《长方体和正方体》这一单元内容，数量关系繁多。在解决此类问题时，各种已知条件越来越复杂，让部分学生“无从下手”。教学中常用事物模型来帮助理解数量之间的关系，但是因为实物的直观形象，生动有趣，学生容易把注意力全部放在操作的实物上，意识中就忘记了“数”的存在。而“画图”——既扬数所长、又取形所优，使得“数量关系”与“空间形式”交相辉映，相辅相成。

案例一：化繁为简 引发“画图”的需要

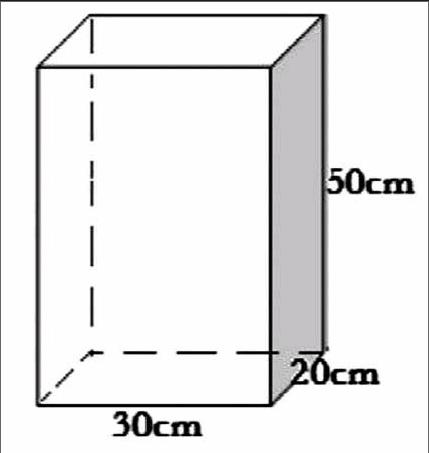
一个长方体玻璃鱼缸，长30厘米，宽20厘米，高50厘米。做这个鱼缸至少需要玻璃多少平方厘米？

针对这一练习，我设计了一个课前小调查：

设计一：抽查20名学生，10分钟时间，独立完成。统计结果：其中画图有3人，解决正确的2人，1人方法正确计算结果出错；不画图的有7人，2人正确，2人计算结果出错，3人没有在规定的时间内做出来。除了计算错误，其它学生错因：一是搞不清楚需要计算哪些面的面积；二是在文字叙述中分不清楚每个面上所对应的数据。而利用画图解决问题的学生除了计算错误之外，都能选择正确的方法进行解决问题。

由此看出：只有少数的学生通过画图解决问题，大多数的学生没有利用画图，帮助解决问题的习惯，而是直接做题，导致不能很好地理解数量之间的关系，出错率较高。怎样才能让学生通过画图解决实际问题呢？让“画图”成为学生发自内心学习需要？

针对学生情况，我又重新设计这样的生活情境：

设计二：我决定定做这样一个长是30厘米，宽是20厘米，高是50厘米的玻璃无盖鱼缸，请同学们思考，你能提出什么数学问题？

生1：如果把金鱼缸放在桌子上，需要在桌子上留出多大的面积？

生2：制作这个金鱼缸需要多少玻璃？

生3：把金鱼缸放在客厅需要预留多大的空间？

生4：如果忽略厚度金鱼缸大约可以装多少升水？

在学生的提问中，形成了一个较为杂乱的生活数学情景，我引导学生依次整理并呈现了这些问题。学生自己读题，很快就有学生说：“怎么这么多问题？”还有的学生说：“太多问题了，我得好好想想求的都是什么？”我顺势引导说：“那可以用什么方法来帮助我们更清楚地理解题目所给的信息和所求的问题呢？”学生回答：“拿一个长方体的物体比一比，看一看。”有的学生说：“画一个长方体的图”。有的学生拿长方体的实物如文具盒、数学书等比一比，看一看；有的学生则动笔画起图来。

在接下来的汇报交流中，用实物比一比的同学除了结合实物还要去题中寻找对应的数据，讲解时有些混乱，且不够直观。而选择画图的同学结合图形既能表达出求的是什么，还能清晰看到所需数据是多少。选择画图的同学优势明显就显示出来了，汇报时结合图形清晰明了有层次。

这时引导学生进行比较：这两种方式，你喜欢哪种，为什么？

生：画图。因为画图整理的直观一目了然，更便于理解。

在此基础上引导学生：“我们解决问题时，往往看到的是抽象冗长的文字信息，这时不妨利用“画图”，将题中的信息在图中表示出来，化繁为简，帮助我们解决问题”。

此时，大多数学生感悟到画图不仅能把繁杂的文字化为简单的图形，既直观形象又有条理地表示数量，需要使得理解题意过程可视化。学生在运用“画图”策略解决数学问题中也尝到了甜头，产生了“画图”的需求。

案例二：抓住“关系”？体现”画图”的优势

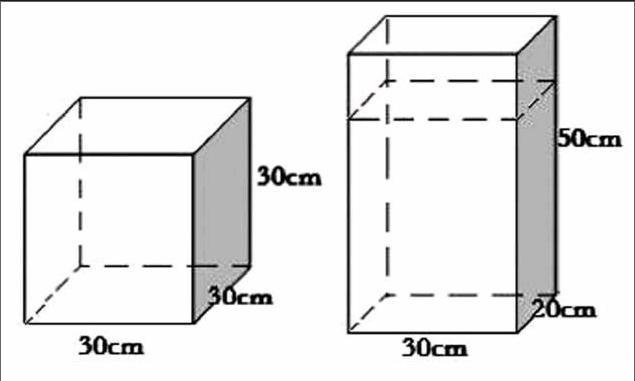
一個从里面量棱长是30厘米的正方体容器装满了水，现将水全部倒入长30厘米，宽是20厘米，高是50厘米的鱼缸容器中，水面离容器口有多少厘米？

在解决问题时，我们就可以利用图形的直观性，引导学生观察思考，寻找数量之间的关系，来帮助学生更好地理解变与不变的数量关系，是正确的解决问题的关键。

学生在解决问题时结合图形进行分析解决，不仅讲的清楚，其他同学也能听得明了。

生1：水的体积就是棱长30cm的正方体的体积：30×30×30=900×30=27000（立方厘米）

水现在的高度：27000÷30÷20=900÷20=45（cm）

水面离容器口距离：50-45=5（cm）

生2：水的体积：30×30×30=900×30=27000（cm3）

长方体的容积：30×20×50=600×50=30000（cm3）

30000-27000=3000（cm3）

水面离容器口距离：3000÷30÷20=100÷20=5（cm）

在这两种方法中，学生能通过画图很轻松地理解了题意，并能借助图形分析数量关系，寻找到题中水的体积这一不变的量，从而解决数学问题。学生从中体会到，“作图”过程就是梳理、分析数量关系，沟通所学图形间联系的过程，不仅可以把文字叙述的题目形象地表示出来，还可以帮助学生在直观图示下，把枯燥的讲授过程变为动态的探索过程。既训练了学生的思维能力，还能从中深刻地体会到“画图”的妙处，在不知不觉中渗透数学思想，感悟“数形结合”思想的优势。

总之，在教学中，教师要及时引导学生不断地反思解决问题的过程，逐步渗透“画图策略”，将解决问题的思想和方法内化为学生的素质，从而让学生领悟出适合自己的“轻舟”，承载学生的思维向更深处漫溯，在数学的乐园里愉悦地享受遨游。

[ 参 考 文 献 ]

[1]袁晓萍.画出来的精彩.教学月刊小学版，2011.

[2]鲁浩.《数形结合思想教学谈》中小学数学2009年第6期.