人工神经网络的电网故障诊断

朱立忠，程 楠

人工神经网络的电网故障诊断

朱立忠，程 楠

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

电网发生故障后，为能迅速找出发生故障的元件，及时解决故障，提出了人工神经网络诊断方法。采用径向基神经网络(RBF)来进行故障诊断，其具有良好的最佳逼近和全局最优的性能，并对RBF隐含层的中心用K均值聚类算法进行优化，给出了仿真实验结果。仿真实验结果表明:与未优化的网络进行对比，经验证，两种方法均可用于电网的故障诊断。

故障诊断；神经网络；全局优化；聚类算法

由于现在城市电网的大型化和复杂化，各种电力系统[1]故障的发生总是无法避免的。近几年来，各个国家都在着力于研究对电网的故障诊断方法，其中，文献[2]讲述了一种以Petri网应用于电力系统的故障诊断的方法；文献[3]设计了一种基于故障录波信息的调度端电网故障系统软件。文献[4]研究了以一种概率的形式，基于贝叶斯网络的分布式电网故障诊断方法；文献[5]采用电网数学模型的方法，求取电网故障参数的最优解。影响电网故障诊断系统的关键因素在于电网故障诊断系统如何适应复杂的数据环境、复杂电网故障中保护动作行为的分析等等。本文针对复杂的数据环境，采用人工神经网络的方法对电网进行诊断。

1 SCADA

SCADA[6]是数据监测与监控系统。当电网发生故障时，与故障元件相关的保护装置因检测到故障症状而使保护动作，驱动对应的断路器跳闸，并将保护动作和断路器跳闸的告警信息实时上报给调度中心的SCADA系统。然而，SCADA系统除了接收电网故障引起的保护动作，开关跳闸等告警信息外，在电网运行中还会不断接收电压越限，装置异常，控制回路断线等方面的告警信息，并将这些告警信息按照时间的顺序以信息流的顺序进行记录，该系统可以记录电网运行过程所有数据。

2 神经网络

常用于故障诊断的神经网络[7]模型一般有:根据采样数据的特点，分为二值输入和连续值输入；又根据神经网络学习的特点，分为有导师学习和无导师学习。基于二值输入的有导师神经网络一般有Hopfield网络[8]；基于二值输入的无导师神经网络一般有ART网络[9]。基于连续值输入的有导师神经网络一般有BP网络和RBF网络；基于连续值输入的无导师神经网络一般有Kohonen网络[10]。该系统采用的是有导师网络中的RBF神经网络。

有导师神经网络用于故障诊断一般是离线过程，其学习与其使用过程是分开来的。当把故障信息输入到神经网络中去，网络经过自组织，自学习的过程，输出合理的故障诊断结果，然后去维修。RBF神经网络，它具有唯一最佳逼近的特性，且无局部极小问题，并且具有较强的输入和输出映射功能，学习过程收敛速度快，这些特点使得RBF神经网络在处理非线性问题中得到广泛的应用。

3 实例分析

验证RBF神经网络在电网故障诊断[11]的实用性，给出一个局部电网模拟图，如图1所示。

图1 局部电网模拟

输入变量即为特征变量，具有一般性，选取具有代表性的电网性能指标:变压器，电动机，线路的电容与电压以及线路电流，分别用x1,x2，…，x7表示。根据经验所得:电网故障[12]一般有三种:输电线故障、母线故障、变压器故障。图1中，B代表母线；L1代表线路；T1代表变压器；CB表示断路器。由SCADA系统得到的因故障而保护的CB2，CB4，CB7，CB9，CB13，CB15动作跳闸，可有实时分析得到一个虚线网络，假设该虚线网络就是要找的故障目标区域，该区域中的原件T1、(B1、B2)、L1、T4可能是故障元件，因此只需要对以上几个元件进行故障诊断即可，也能够提高诊断的效率。

数据预处理:由于径向基函数依赖于输入样本数据，而在电网中测得的样本数据比较大，这样大的数据容易导致计算复杂，训练时间及其长，为避免该情况，将各个样本数据进行归一化。归一公式如下:

归一化的数据在[-1，1]之间，训练样本与测试样本采用以上给出的归一法，训练样本和测试样本3均是采用归一化得到的数据，样本数据见表1。

表1 样本数据

续表

网络的期望输出为:每一输出Y都对应6位数据，故障表达的方式有6种，如表2所示。

表2 故障表示

因此其期望输出为:

[0 1 0 0 0 0;0 0 0 0 0 1;[ T1T4

0 0 1 0 0 0;0 0 0 1 0 0;B1B2

0 0 0 0 1 0;0 0 0 0 0 0;L1无故障

0 1 0 0 0 0;0 0 0 0 0 1;T1T4

0 0 1 0 0 0;0 0 0 1 0 0;B1B2

0 0 0 0 1 0;0 0 0 0 0 0;L1无故障

0 1 0 0 0 0;0 0 0 0 0 1;T1T4

0 0 1 0 0 0;0 0 0 1 0 0;B1B2

0 0 0 0 1 0;0 0 0 0 0 0;L1无故障

0 1 0 0 0 0;0 0 0 0 0 1;T1T4

0 0 1 0 0 0;0 0 0 1 0 0;B1B2

0 0 0 0 1 0;0 0 0 0 0 0;L1无故障

0 1 0 0 0 0;0 0 0 0 0 1;T1T4

0 0 1 0 0 0;0 0 0 1 0 0;B1B2

0 0 0 0 1 0;0 0 0 0 0 0;] L1无故障]。

用RBF神经网络进行训练，设定样本目标的误差为0.01，扩展系数为1，训练次数为1000，用Matlab进行仿真得到的网络误差训练曲线如图2所示。

图2 RBF网络误差训练曲线

由图2可以观察到，当训练次数达到11次，神经网络已经很好地收敛于预期的期望输出。同时得到了隐层单元的阈值b1=[0.8326 0.8326 0.8326 0.8326 0.8326 0.8326 0.8326 0.8326 0.8326 0.8326 0.8326]，网络的输入层到隐层单元的权值为w1=

[0.65400.41900.66701.32000.3210-1.0810-0.91200.35500.20000.39900.01100.2180-0.4230-0.29900.36200.25600.37500.23200.1120-0.4670-0.37800.72800.53400.49901.10000.3300-1.1780-0.90000.43800.23200.51700.50300.1630-0.5120-0.54300.42100.21400.46700.00100.2560

-0.4190-0.43200.32500.12800.23400.36700.1010-0.6710-0.36800.80300.42900.51800.98700.2360-0.9430-0.83500.33200.21200.39000.11100.2230-0.4720-0.21900.36700.18900.11200.98900.2000-1.0000-0.96800.88500.42900.88300.40100.1890-0.8910-0.7850],

输出层的阈值为b2=[0 5.0223 -5.7455 0.5024 0.7796 0.1566]，隐层单元到输出层的权值为w2=[0 0 0 0 0 0 0 0 0 0 0

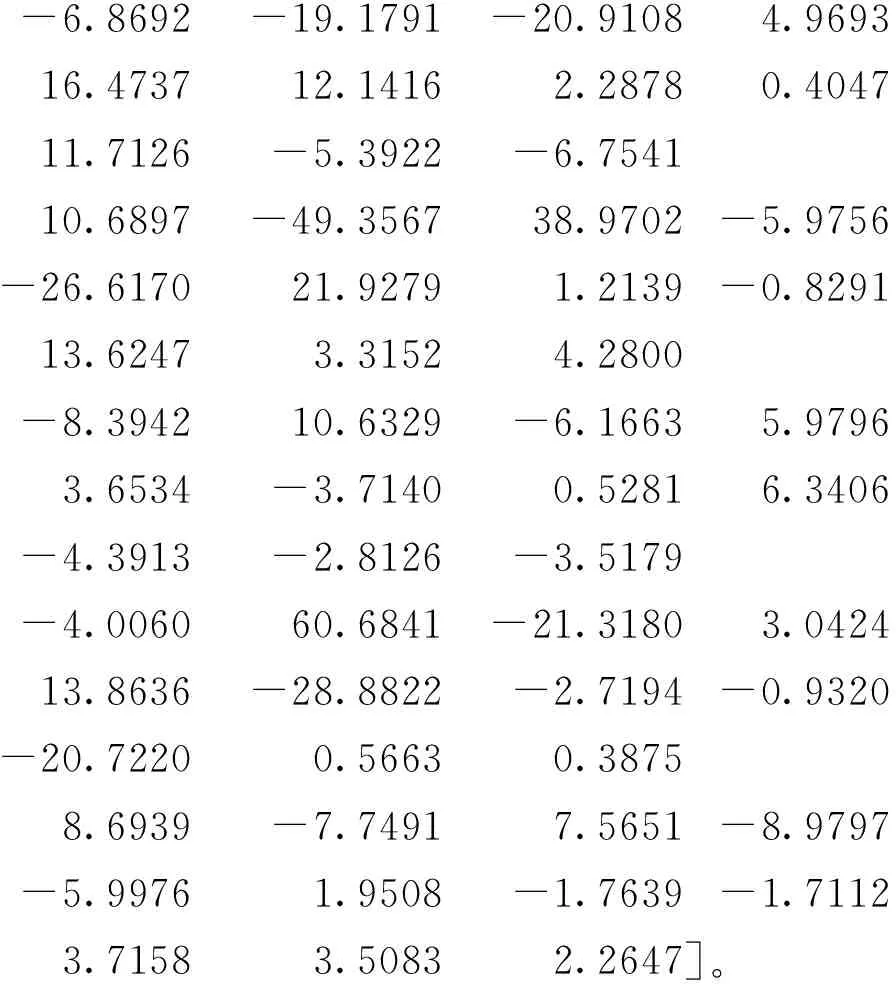
-6.8692-19.1791-20.91084.969316.473712.14162.28780.404711.7126-5.3922-6.754110.6897-49.356738.9702-5.9756-26.617021.92791.2139-0.829113.62473.31524.2800-8.394210.6329-6.16635.97963.6534-3.71400.52816.3406-4.3913-2.8126-3.5179-4.006060.6841-21.31803.042413.8636-28.8822-2.7194-0.9320-20.72200.56630.38758.6939-7.74917.5651-8.9797-5.99761.9508-1.7639-1.71123.71583.50832.2647]。

还对RBF网络的隐含层的中心[13]用K均值聚类算法进行优化，选取7组样本进行测试，其测试样本数据如表3所示。

表3 测试样本数据

在聚类确定数据中心的位置之前，需要先估计中心的数目(隐层节点的数目)，用K均值聚类算法[14]的步骤如下:

变量定义:{X1，X2，…，Xp}为p个样本；M为隐含层的节点数目；C(k)为第k次迭代时的中心。

(1)初始化，选择M个不相同的向量作为初始聚类中心，C1(0)，C2(0),……,CM(0)。

(2) 计算输入各样本点与聚类中心点的欧式距离并求出最小距离的节点[15]

dj(k)=‖Xp-Cj(k)‖,p=1,2,…,30，

j=1,2,…,M。

(3)对每一输入样本Xp根据与其聚类中心的最小欧式距离进行归类为r(Xp)，当r(Xp)=min‖Xp-Cj(k)‖,p=1,2,…30,Xp被归为第r类，从而将样本化为M个子集，每个子集构成一个以聚类中心为代表的聚类域。

(4)更新各个聚类的中心。当

q为学习效率，0

(5)令k=k+1，重复上述过程，直到Cj(k)的改变量小于预设阈值。

经优化中心的网络的测试输出结果:

测试样本的输出结果Y′=

[00.68430.4380-0.0086-0.0851-0.00340-0.02070.00260.1025-0.00350.79100-0.25301.10260.03820.2125-0.10560-0.03910.00090.8783-0.00850.016500.05840.1037-0.00250.84780.003400.3239-0.0035-0.08330.04350.274800.5759-0.0156-0.17110.08450.3542];

隐含层到输出层的权值:

W2′=[0 1.0019 -0.2872 0.1037 0.0255 -0.4014

0-0.33920.0052-0.3911-0.05010.85680-1.01851.83250.0976-0.7129-0.25020-0.41120.00921.5376-0.0601-0.86330-0.3360-0.59780.12851.2974-0.42270-0.61980.04660.1357-0.0864-0.5330]。

该测试样本的网络误差曲线如图3所示。

图3 测试样本的网络误差曲线

此优化的RBF网络[16]的误差曲线几乎逼近图2所示的曲线，该网络的预测结果较好，但是步长却明显缩短，更节省时间。

4 结束语

当电网发生故障时，找出可能发生故障的元件，并将故障区域缩小，并用RBF神经网络作为模式匹配器，将神经网络的输出作为判断故障类型的识别，后用K均值聚类法优化RBF神经网络的隐含层的中心，经仿真后，与未优化的神经网络相比，步长明显缩短，更节省时间，诊断效果较好，该方法可为电网的故障诊断提供参考。

[1]张朝海.电力系统运行与控制[D].广州:华南理工大学,1996.

[2]Armen Aghasaryan,Eric Fabre,Albert Benveniste.Fault Detection and Diagnosis in Distributed Systems:An Approach by Partially Stochastic Petri Nets[J].Discrete Event Dynamic Systems,1998,82(6):1121-1196.

[3]Bandler J W,Salama A E.Fault Diagnosis of Analog Circuits[J].Proceedings of the IEEE,1985,73(8):1279-1327.

[4]周曙,王晓茹,钱清泉.基于贝叶斯网的分布式电网故障诊断方法[J].电网技术,2010,15(9):76-81.

[5]刘道兵,顾雪平,梁海平,等.电网故障诊断完全解析模型的解集评价与最优解求取[J].中国电机工程学报,2014,10(31):5668-5676.

[6]吴文传,张伯明,孙宏斌，等.基于WindowsNT的SCADA/EM S/DTS一体化支撑平台[J].电网技术,1999,6(9):54-59.

[7]梁戈超,何怡刚,朱彦卿.基于模糊神经网络融合遗传算法的模拟电路故障诊断法[J].电路与系统学报,2004,25(2):54-57.

[8]刘晓军.基于神经网络的自适应滤波[J].现代引信,1995,8(2):32-37.

[9]严悦.基于ART神经网络案例匹配的轨道交通智能数据诊断技术研究[D].南京:南京理工大学,2013.

[10]张红斌,贺仁睦,刘应梅.基于KOHONEN神经网络的电力系统负荷动特性聚类与综合[J].中国电机工程学报,2003,12(5):26-34.

[11]冯金刚,潘成胜,李航.基于神经网络的远程网络故障诊断系统[J].沈阳工业学院学报,2002,21(4):62-65.

[12]赵冬梅.基于多信息源的电网故障诊断方法的研究[J].华北电力大学学报,2005,11(4):32-36.

[13]M Catelani,A Fort.Fault diagnosis of electronic analog circuits using a radial basis function network classifier[J].Measurement,2000,18(28):147-158.

[14]宋丽伟,彭敏敏,田成来,等.基于PSO-RBF神经网络的模拟电路诊断[J].计算机应用研究,2012,29(1):72-74.

[15]刘道华,张礼涛,曾召霞,等.基于正交最小二乘法的径向基神经网络模型[J].信阳师范学院学报,2013,30(3):428-431.

[16]熊国江,石东源,竹林.基于多输出衰减径向基函数神经网络的电网故障诊断[J].电力系统保护与控制,2013,11(1):38-45.

(责任编辑:马金发)

Fault Diagnosis of SCADA System for Artificial Neural Network

ZHU Lizhong，CHENG Nan

(Shenyang Ligong University,Shenyang 110159,China)

After a fault happens in order to quickly find the faulty components,in a timely manner to solve fault,artificial neural network diagnosis method is proposed.RBF neural network(RBF)application has good optimal approximation and global to fault diagnosis.The K-means clustering algorithm is optimized to the center of the hidden layer of neural network and it offers the policy experimental results.Simulation results show that both methods can be used in the fault diagnosis of power grid in comparison with unoptimized network.

fault diagnosis;neural network;global optimization;clustering algorirhm

2015-09-15

朱立忠(1967—)男,教授,研究方向:复杂系统故障诊断与监控技术。

1003-1251(2017)01-0102-05

TM711

A