基于灵敏度分析和替代模型的地下水污染风险评价方法
2017-02-22常振波卢文喜顾文龙崔尚进吉林大学地下水与资源环境教育部重点实验室吉林长春130012吉林大学环境与资源学院吉林长春130012
常振波,卢文喜*,辛 欣,顾文龙,崔尚进(1.吉林大学,地下水与资源环境教育部重点实验室,吉林长春 130012;2.吉林大学环境与资源学院,吉林 长春 130012)
基于灵敏度分析和替代模型的地下水污染风险评价方法
常振波1,2,卢文喜1,2*,辛 欣1,2,顾文龙1,2,崔尚进1,2(1.吉林大学,地下水与资源环境教育部重点实验室,吉林长春 130012;2.吉林大学环境与资源学院,吉林 长春 130012)
采用蒙特卡洛方法,借助随机模型进行地下水污染风险评价,模型中随机变量利用灵敏度分析的方法确定,使地下水风险评价结果更为可靠,并借助一个假想例子来说明评价过程.结果表明,模拟输出数据符合正态分布规律,对正态分布概率密度函数积分可以得到污染风险,井1、井2和井3的污染风险分别为0%、78.52%和100%;根据整个模拟区的污染风险分布图可以划分出具有不同污染风险程度的子区域,藉此能够定量评价模拟区不同子区域的污染风险程度.
地下水污染风险评价;灵敏度分析;蒙特卡洛;替代模型;概率统计
地下水人为污染事件时有发生[1],相比地表水污染,地下水污染修复所需费用更高.地下水污染具有发生的隐蔽性和发现的滞后性[2-3],污染一经发现难以修复.为了缓解地下水质恶化的现状,可靠的地下水污染风险评价工作是十分必要的.决策者可以根据风险评价结果,通过人为规划和调控降低污染发生的可能性[4-5].
风险评价实质就是不确定性分析,没有不确定性,就没有风险[6].因此,对地下水溶质运移中不确定性因素进行定量分析,并在结果中体现风险程度,可以使地下水污染风险评价结果更加科学.对此国内外展开了大量的研究,Goodrich等[7]应用蒙特卡洛模拟,研究由于参数不确定性导致地下水流和溶质运移过程的不确定性;Bennett等[8]将蒙特卡洛方法得到的一系列污染物迁移结果用于暴露评价;梁婕[9]利用贝叶斯方法推断出渗透系数随机场的相关参数的后验分布,基于参数的后验分布研究地下水溶质运移规律;申升[10]进一步考虑了纵向弥散度对地下水溶质运移的影响.
前人研究中随机变量多为事先确定,然而对于不同的模型参数对结果的影响是不同的,引入灵敏度分析方法,筛选对结果影响较大的参数作为随机变量,利用蒙特卡洛方法对地下水溶质运移进行不确定性分析,并以浓度值超过某一限定值的概率作为污染风险,对整个模拟区的污染风险进行定量评价.为了减少大量重复调用模拟模型而产生的计算负荷,本文借助替代模型完成蒙特卡洛过程.
1 研究方法
1.1 蒙特卡洛法
蒙特卡洛法作为最常用的不确定性分析方法之一被广泛地应用于地下水数值模拟中[11-13].蒙特卡洛方法就是通过设置一系列平行的确定性实验来模拟随机问题.在设置平行实验时选择待求因素作为随机变量,研究随机变量变化对结果的影响.蒙特卡洛法将参数的不确定性转化为溶质运移的不确定性,能够很好地表征污染风险[14-15].本文以蒙特卡洛方法作为框架,具体研究思路如图1所示.
1.2 灵敏度分析
灵敏度分析可以定量地评价参数不确定性对结果造成的影响,本文利用灵敏度分析的方法分析参数对输出浓度的影响,挑选两个灵敏度系数较大的参数作为随机变量,进行地下水污染风险评价,这样会使得风险评价更为可靠.分析方法可分为全局灵敏度分析和局部灵敏度分析,其中局部灵敏度分析能得到单一参数变化对结果的影响.灵敏度利用结果对参数求偏导数,反映参数变化对结果的影响程度[16-17],即:

式中:Sk表示当参数αk变化时对输出结果y的影响程度,也就是灵敏度系数.
对于某一特定参数灵敏度系数的求解,可通过以下方法近似,使该参数的值由αk变化为αk+Δαk,结果则由 yi( αk)变化为 yi( αk+Δαk),可用以下公式求得近似值,即:
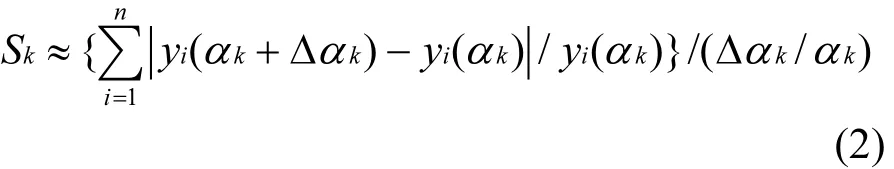
1.3 替代模型
少量的数据无法支撑地下水污染风险评价,而大量数据的获取需要大量的时间,其中时间主要花费在模拟模型的求解上.为了减少模拟模型的使用次数,引入替代模型.替代模型能够在某些行为上逼近模拟模型,且调用简便,运行时间短.蒙特卡罗模拟与替代模型结合能有效减小计算负荷[18-19].
克里格方法利用协方差的变化来表达空间的变化,现被延伸为一种替代模型的建立方法,广泛地应用于多个行业,是一种黑箱模型[20].
克里格模型的方程可以表示成以下形式:

上述对 y( x)的估计值yˆ( x)可以分为两部分,其中前一部分为线性回归部分,后一部分为随机部分.其中 f( x) =[f1( x) , f2(x) ,… , fk(x )]为已知回归模型的基函数;待定参数 β = [β1, β2,… ,βk],可以通过训练数据求得;z( x)为随机部分,其方差为σ2,均值为0,协方差:

R( xi, xj)为采样点xi和点xj的关联函数,有多种类型可供选择,本文采用较为常用的高斯模型:
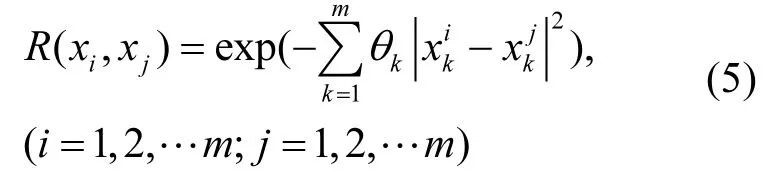
式中:θk为待定参数,通过求解优化模型求得;xki为第i个样本的k维坐标.
根据克里格模型,在预测点 x处的响应值y( x)的预测估计值为:

式中:f为基函数,为方便起见,本文选择常数型,f为一常数列向量;r( x)为点x与n个训练样本采样点 (x1, x2,… ,xn)之间的相关向量,;y为与n个采样点对应的响应值,为 n×1的向量;β为线性回归部分的待定参数,可以通过最优线性无偏估计求得:

R为n个采样点的相关矩阵:
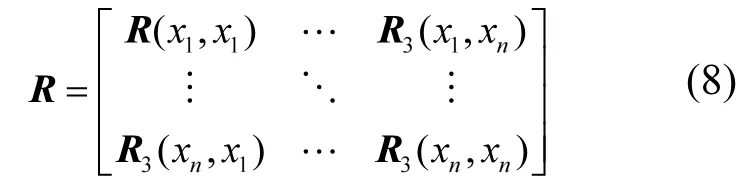
方差σ2的估计值为:

待定参数 θk可以通过一个无约束优化问题求得:
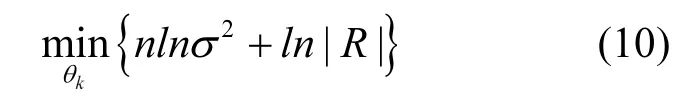
通过MATLAB软件实现上述替代模型的建立过程.
2 假想算例
2.1 概况

图1 技术路线流程Fig.1 The flow chart of technical route
模拟区内存在二维均质各向同性潜水含水层,含水层信息如图1所示,含水层厚为12m,模拟区初始水位为8m,水力梯度约为0.007,年平均降水量730mm,降雨入渗系数为0.2,选择渗透系数、给水度、纵向弥散度和孔隙度4个参数进行灵敏度分析,根据经验给出其取值范围和概率分布,如表1所示,其中因横向弥散度与纵向弥散度的比值为 0.1,故只考虑纵向弥散度.区内共设三口抽水井,定流量抽水,各井抽水量均为300m3/d,持续时间 1a,同时将抽水井作为水质观测井.现假设在模拟区内建造一座工厂,工厂每天向含水层排放400m3的污水,污染物浓度500mg/L,污染质为保守物质,迁移过程中不发生物理化学反应.含水层污染物的初始浓度为零,定水头边界可以视为零浓度边界,隔水边界可以视为零通量边界.

表1 参数的概率分布及取值情况Table 1 The probability distribution and values information of parameters
2.2 随机模型建立
2.2.1 数学模型 地下水溶质运移模型是在地下水水流模型的基础上建立的,研究区地下水为二维均质各向同性潜水非稳定流,可以建立数学模型:

地下水溶质运移数学模型:

地下水水流模型和溶质运移模型通过达西定律联系起来:

式中:K为含水层的渗透系数,m/d;H为潜水水位, m;B为潜水含水层底板高程,m;P 为人工开采强度,m/d;R为降水入渗补给量,m/d;µ为含水层给水度,无量纲;G为模拟区范围;S1、 S2为含水层边界,在水流模型中为定水头边界,在溶质运移模型中为定浓度边界;S3、 S4为含水层边界,在水流模型中为零流量边界,在溶质运移模型中为零弥散通量边界;Kn为边界法向量上的渗透系数,m;n为含水层介质的孔隙度,无量纲;c为污染质浓度,mg/L;Dx、Dy为水动力弥散系数在x、y方向的分量,m2/d;vx、 vy为渗透流速v在x、y方向上的分量,m/d.

图2 研究算例平面示意Fig.2 Plan view of the aquifer configuration
数学模型是借助GMS软件的MODFLOW模块和MT3DMS模块进行求解的.
2.2.2 随机变量确定 本文利用灵敏度分析的方法确定随机变量,参与分析的参数有渗透系数K、给水度µ、纵向弥散度 αL和孔隙度n.由图3可知,4个参数的灵敏度系数由大到小依次为SK、 Sα、Sn、 Sμ,渗透系数和纵向弥散度的灵敏度系数较大,选择这两个参数作为随机变量,按照其经验概率分布进行取值,剩下的两个参数作为确定值输入模型.
2.3 替代模型的建立
利用拉丁超立方抽样的方法对随机变量渗透系数和纵向弥散度按照其概率分布进行抽样,得到50组输入数据集,将50组参数组合分别输入模拟模型,利用GMS求解,得到50组输出结果.将参数组合和输出结果中三口观测井的末时刻浓度值分别作为输入输出,利用40组输入和输出建立克里格替代模型,并利用 10组数据(每一组数据均包括3口观测井的浓度值)验证替代模型的可靠性.图4为模拟模型输出结果和替代模型输出结果对比图,可以看出二者的相对误差在2%以下,可认为替代模型满足误差要求,并能够替代模拟模型进行调用.

图3 参数灵敏度曲线Fig.3 Sensitivity curves of parameters
2.4 蒙特卡罗模拟
利用蒙特卡罗方法模拟500次试验,对结果进行统计.即首先根据渗透系数和纵向弥散度的概率分布,按照拉丁超立方抽样的方法,得到500组输入数据集;然后将500组参数组合输入替代模型,得到 500组输出数据;对输出数据进行分析.
3 结果分析
3.1 单井污染风险分析
利用SPSS软件中的单样本K-S检验分析500组输出,假设三口井的浓度值为正态分布,可以得到结果如表 2所示,其中当 P值大于 0.05时认为假设成立,得到三口井的分布均为正态分布.由此画出三口井浓度值的累积频率直方图和其对应的正态分布概率密度函数,如图5(a)~(c)所示.

图4 模型预测结果对比Fig.4 Comparison of different models’ result

表2 输出数据单样本K-S分析结果Table 2 The results of K-S single sample analysis on output data

图5 观测井污染物浓度值直方图及正态分布概率密度函数Fig.5 Observation wells pollutant concentration histogram and normal probability density function
分析三口供水井的污染风险,以污染物浓度值超过100mg/L的地下水为是被污染的,将超过100mg/L概率作为污染风险大小,利用如下公式可计算三口井污染风险:

式中:P为单井污染风险大小;()f x为单井浓度值的概率密度函数;σ为正态分布的标准差;µ为概率分布的均值.井1、井2和井3的污染风险分别为0%、78.52%和100%.由此可以得到,井2和井3水质均有较大的污染风险,为此可能要对工厂排放污水的浓度做出一定的限制或者寻找新的供水井,下面通过对区域的污染风险进行评价来为寻找新的供水井提出一些建议.
3.2 区域污染风险分析

图6 模拟区污染风险分布Fig.6 the pollution risk distribution map of the whole simulation area
为更加全面地分析整个研究区的污染风险,计算出每个离散网格所对应位置的污染风险,并绘制等值线图见图 6.可以看出污染风险在不同空间位置上具有差异性,研究区上方区域污染风险较小且范围较小,下方区域污染风险较大且范围较大.井1位于白色区域即污染低风险区域,在此区域的地下水受到污染的风险较小,低于20%;井2位于浅色区域即污染中等风险区域,此区域地下水受到污染的风险在20%到80%;井3位于深色区域即污染高风险区域,此区域地下水受到污染的风险在80%以上.井2和井3均有较高的污染风险,为了使地下水水质能够维持使用标准,需要寻找新的供水井.图中白色区域风险小,且靠近定水头边界水量充足,可以在此区域内选择新供水井.
4 结论
4.1 在文中假设情境下灵敏度分析方法筛选出渗透系数和纵向弥散度作为随机参数,利用这两个参数作为随机变量得到的地下水污染风险评价结果更加科学和可靠.
4.2 利用本文的方法进行地下水风险评价,能够得到整个模拟区污染风险分布图,根据此图可以确定污染风险小的新供水井位置.
4.3 本文利用蒙特卡罗的方法与克里格替代模型,大大减少了计算负荷,而且克里格替代模型预测结果与模拟模型模拟结果相比,相对误差均小于 2%,说明替代模型可以较好地模仿模拟模型的行为.
[1] 董文福,傅德黔.近年来我国环境污染事故综述 [J]. 环境科学与技术, 2009,32(7):75-77.
[2] 王 昊.我国地下水污染成因及防治措施研究 [J]. 资源节约与保护, 2013(5):88-97.
[3] 王焰新.地下水污染与防治 [M]. 北京:高等教育出版社, 2007.
[4] 张丽君.地下水脆弱性和风险性评价研究进展综述 [J]. 水文地质工程地质, 2006,33(6):113-119.
[5] 刘增超,董 军,何连生,等.基于过程模拟的地下水污染风险评价方法研究 [J]. 中国环境科学, 2013,33(6):1120-1126.
[6] 马禄义,许学工,徐丽芬.中国综合生态风险评价的不确定性分析 [J]. 北京大学学报:自然科学版, 2011(5):893-900.
[7] Goodrich M T, Mccord J T. Quantification of uncertainty in exposure assessments at hazardous waste sites [J]. Ground Water, 1995,33(5):727-732.
[8] Bennett D H, James A L, Mckone T E, et al. On uncertainty in remediation analysis: variance propagation from subsurfacetransport to exposure modeling [J]. Reliability Engineering and System Safety, 1998,62(1/2):117-129.
[9] 梁 婕.基于不确定理论的地下水溶质运移及污染风险研究[D]. 长沙:湖南大学, 2009.
[10] 申 升.基于贝叶斯理论的地下水溶质运移的不确定性研究[D]. 长沙:湖南大学, 2012.
[11] 王 宇,卢文喜,卞建民,等.基于小波神经网络的地下水流数值模拟模型的替代模型研究 [J]. 中国环境科学, 2015,35(1):139-146.
[12] 欧阳琦,卢文喜,侯泽宇,等.基于替代模型的地下水溶质运移不确定性分析 [J]. 中国环境科学, 2016,36(4):1119-1124.
[13] 曾献奎,王 栋,吴吉春.地下水流概念模型的不确定性分析 [J].南京大学学报(自然科学), 2012,48(6):746-752.
[14] 姚磊华.白杨水源地潜水水质的 Monte—Carlo随机模拟 [J].长春科技大学学报, 1998(3):296-302.
[15] Hamed M M, Conte J P, Bedient P B. Probabilistic screening tool for ground-water contamination assessment [J]. Journal of Environmental Engineering, 1995,121(11):767-775.
[16] 束龙仓,刘佩贵,刘 波,等.傍河水源地数学模型的参数灵敏度分析—以辽宁省北票市某傍河水源地为例 [J]. 工程勘察, 2006,(8):29-31.
[17] 束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析 [J]. 河海大学学报(自然科学版), 2007,35(5):491-495.
[18] 安永凯,卢文喜,董海彪,等.基于克里格法的地下水流数值模拟模型的替代模型研究 [J]. 中国环境科学, 2014,34(4):1073-1079.
[19] 顾文龙,卢文喜,马洪云,等.地下水数值模拟分析中降水入渗补给强度及渗透系数不确定性评价 [J]. 水电能源科学, 2015(11): 45-48.
[20] 吴义忠.多领域物理系统的仿真优化方法 [M]. 北京:科学出版社, 2011.
Groundwater contamination risk assessment method based on sensitivity analysis and surrogate model.
CHANG Zhen-bo1,2, LU Wen-xi1,2*, XIN Xin1,2, GU Wen-long1,2, CUI Shang-jin1,2
(1.Key Laboratory of Groundwater Resources and Environment Ministry of Education, Jilin University, Changchun 130012, China;2.College of Environment and Resources, Jilin University, Changchun 130012, China). China Environmental Science, 2017,37(1):167~173
Stochastic model with Monte Carlo method was used to assess the risk of groundwater pollution. The random variables in the model were determined by the sensitivity analysis, which made the result of the groundwater risk assessment more reliable, and the evaluation process was illustrated by a hypothetical example. The results showed that the simulated output data was in accord with the normal distribution law, and normal probability density function of the integrator was the risk of contamination. The pollution risks of well 1, 2 and 3 were 0%, 78.52% and 100%, respectively. Sub regions with different risk of pollution were divided according to the pollution risk distribution map of the whole simulation area, so as to quantitatively evaluate the pollution risk of different sub area in the simulation area.
groundwater contamination risk assessment;sensitivity analysis;Monte Carlo;surrogate model;probability statistics
X703
A
1000-6923(2017)01-0167-07
常振波(1993-),男,河南开封人,吉林大学硕士研究生,主要从事地下水溶质运移的不确定性研究.
2016-05-15
国家自然科学基金项目(41372237);吉林大学研究生创新基金资助项目(2016207,2016100)
* 责任作者, 教授, luwenxi@jlu.edu.cn
