采用波束域加权的大迎角飞行姿态控制算法

陆兴华

(广东工业大学华立学院，广东 广州 511325)

采用波束域加权的大迎角飞行姿态控制算法

陆兴华

(广东工业大学华立学院，广东 广州 511325)

无人机在姿态角变化剧烈、大迎角等极端状态飞行时，参数在有限个线性模型之间连续变化，会带来系统参数的不确定性，飞行姿态控制的难度加大。提出一种基于波束域加权谱峰搜索方法进行误差补偿和自适应控制的无人机大迎角飞行姿态控制算法。构建无人机在俯仰、偏航和滚动飞行下的运动状态方程，采用波束域加权谱峰搜索方法，不断地对系统参数进行测量，进而根据姿态参量测量而对模型进行修正，提高控制性能，修正航向偏差。经过不断的最优自回归和最小二乘拟合，得到最优的输出姿态角，实现偏航纠正和误差补偿。仿真结果表明，利用算法进行无人机大迎角飞行姿态控制，偏航修正和误差补偿的性能较好，控制的鲁棒性和收敛性较高。

无人机；自适应控制；误差补偿；波束域加权

0 引 言

无人机的稳定性飞行控制一直是制约无人机发展的一个重要瓶颈技术。无人机在整个纵平面飞行过程中，控制器参数在有限个线性模型之间连续变化，会带来系统参数不确定的问题。无人机在极端状态下飞行的迎角和气动特性导致飞行姿态不稳定，需要通过飞机惯导优化控制设计，进行扰动抑制，防止飞机翻滚和失衡。研究无人机在姿态角变化剧烈、大迎角飞行等极端情况下的稳定性控制算法，使得无人机能保持较好飞行姿态稳定性，提高无人机的抗扰动能力，越来越受到重视[1]。

在极端飞行状态下，无人机飞行控制系统是一个多变量，非线性，强耦合系统。传统的控制算法采用多参量循环跟踪控制的无人机飞行姿态稳定性控制方法，存在较大的稳态误差[2-3]。对此，相关文献进行了控制算法的改进设计。其中，文献[4]提出一种基于模糊神经网络控制的智能无人机的飞行控制方法，设计模糊神经网络控制器用于抑制抖振的边界层，减少稳态误差，提高了飞控系统的稳定性，但是该方法具有计算开销较大、实时性不好的问题。文献[5]提出一种基于惯导失衡补偿的无人机飞控系统设计方法，采用Lyapunove稳定性泛函方法进行反演控制，将无人机的飞行惯导的非线性系统进行分解，提高了大迎角飞行跟踪控制能力，但是该方法在处理无人机不确定动态系统的控制问题上具有收敛性不好的缺点。

针对上述问题，文中提出一种采用波束域加权谱峰搜索方法进行误差补偿和自适应控制的无人机大迎角飞行姿态控制算法。构建了无人机大迎角飞行的运动数学模型，采用波束域加权谱峰搜索方法构建无人机大迎角飞行的自适应跟踪控制器，实现控制算法改进。仿真实验验证了该算法的优越性能。

1 无人机姿态控制原理及大迎角飞行的运动数学模型

1.1 无人机姿态控制原理与问题描述

针对无人机飞行稳定性控制和姿态控制方面的问题进行研究，控制算法改进设计是整个无人机控制系统设计的核心，文中提出一种基于波束域加权谱峰搜索的无人机控制算法。在算法描述之前，需要先建立无人机的纵向运动模型[6]。以小扰动为干扰背景，根据姿态参量测量模型，无人机飞行姿态控制器建立在如下几个坐标系基础上。

(1)速度坐标系Ox3y3z3：无人机动力系数通过速度坐标系构建初始运动方程。假设坐标系的原点O；选取p个分布式目标的速度矢量V为Ox3轴；对目标方位角进行误差收敛，假设Oy3轴与Ox3轴垂直，且位于无人机大迎角飞行的纵向对称面内，向上为正；目标信号源的法相坐标Oz3轴垂直于Ox3y3平面，其方向按右手定则可以确定飞行偏航角和侧滑角。

(2)偏航坐标系Ox1y1z1：偏航坐标系与无人机的滑翔翼固连。无人机飞行过程的质心为坐标原点O；Ox1指向无人机的正航向，与飞机的纵轴重合；Oy1向上为正，在纵对称平面内，中心波达方向θi和扩展为σi；Oz1按右手定则确定。

(3)操纵运动坐标系Ox2y2z2：操纵运动坐标系的稳态中心矢量为坐标系原点；选取无人机航向偏差的速度矢量V为Ox2轴；Oy2轴在一个铅垂平面内，只关心目标的方位，向上为正；Oz2轴按照方位估计确定。

(4)大地坐标系Axyz：大地坐标系是一种与地球进行固连的坐标系。无人机在做大迎角飞行时，对应的谱峰位置即目标的方位角，Ay轴与地面垂直，向上为正，对目标方位角和扩展角进行偏航控制，Ax以发射方向为正，坐标系的侧滑角Az轴按右手定则确定。

在上述无人机飞行的坐标系体系中，构建无人机大迎角飞行的运动方程，包括无人机飞行的直度角和偏航角运动方程，根据动量矩以及飞机的动力学流体控制，按照姿态参量测量而对模型进行修正，克服飞行姿态边界层的稳态误差。

1.2 无人机大迎角飞行的运动数学模型

假定无人机在大迎角飞行时，其纵向运动是对称的，而且无人机的倾斜操纵机构和偏航操纵机构没有动作，通过限定初始状态，采用非线性取代积分进行滑模控制，保证纵向运动对称性的偏转。当无人机在做横滚等运动时，可以得到一个封闭的无人机的空间运动方程组，如式(1)～(8)：

(1)

(2)

(3)

(4)

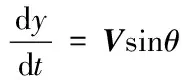
(5)

(6)

α=ϑ-θ

(7)

δz=f(e1)

(8)

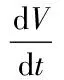
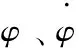
(9)

(10)

(11)

通过以上原理，当无人机飞行载体处于任意姿态时，可以在大扰动条件下构建无人机大迎角飞行的姿态控制模型，进行飞行姿态的自适应跟踪控制，采用波束域加权谱峰搜索方法进行误差补偿和自适应控制，构建控制器，实现控制算法改进。

2 波束域加权谱峰搜索及控制算法改进的设计与实现

2.1 基于波束域加权谱峰搜索的控制误差补偿

在上述构建的无人机飞行姿态控制坐标系和运动方程的基础上，进行飞行姿态控制算法设计。传统方法在大的初始误差条件下会使系统的暂态性能弱化，甚至可能出现积分windup效应[7]，导致整个系统的不稳定。为了克服传统方法的弊端，提出采用波束域加权谱峰搜索方法进行误差补偿和自适应控制，实现控制算法改进。假设无人机飞行的控制参量约束相干分布源模型为：

(12)

其中

(13)

(14)

无人机捷联惯导矢量z(t)的协方差矩阵可以表示为：

(15)

其中，B=[b1(θ1),b2(θ2),…,bq(θq)]T。

无人机在运动过程中姿态会不断变化，飞行初始导引段的协方差矩阵的波束域奇异值分解为：

(16)

(17)

若无人机飞行控制信号源未知参数只有两个，分别为中心波达方向θi和噪声偏差σi，对应姿态角误差补偿和自适应跟踪的状态方程为：

(18)

当满足：

bi(θi)=Φ(θi)hi

(19)

hi为实数矢量，无人机大迎角飞行的姿态角误差收敛到零，通过波束域加权谱峰搜索，实现两时刻偏航和导引误差融合和自适应补偿，提高了控制精度。

2.2 控制算法改进实现

(20)

在连续的快拍之间进行波束域加权控制，有span{Us}=span{A(θ)}，此时存在一个满秩矩阵T使得飞行姿态控制的谱峰最大，有Us=A(θ)T。由此，控制参量的输出优化问题转化为求如下方程的极小化解的问题：

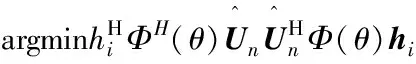
(21)

由上所述，计算输出控制误差的二阶中心矩，经过不断的最优自回归和最小二乘拟合，得到最优的输出姿态角，实现偏航纠正和误差补偿，提高飞行姿态控制的自适应跟踪控制能力。

3 仿真实验与结果分析

通过仿真实验测试文中算法在实现无人机飞行姿态控制中的性能。实验中，无人机飞行姿态控制系统的信号与信息处理芯片选择了ADI公司的ADSP-BF537，控制系统软件的开发平台是VisualDSP++4.5。经过模拟8通道均匀线列阵A/D采样，进行飞行姿态参量数据的采集，作为控制仿真的原始输入数据。假设数据采样的相邻阵元间隔为λ/2，其中λ对应无人机大迎角飞行下的中心频率的波长。数据采样率≥200kHz，D/A分辨率为12位(至少)，从两个通道的控制输出波达方向为θ1=-15°,θ2=10°，输入姿态数据采样信号源的扩展角度分别为Δ1=5°,Δ2=8°，信噪比为0。在快拍数为1 000下，进行飞行姿态跟踪补偿，采用波束域加权谱峰搜索方法，得到无人机飞行姿态控制的二维谱峰搜索结果，如图1所示。

图1 无人机飞行姿态控制的二维谱峰搜索结果

从图中可见，采用文中方法，考虑了模型的非线性特性和不确定性，采用波束域加权谱峰搜索在线估计未知的对象参数，不断地对系统某些参数进行测量，进而根据姿态参量测量对模型进行修正，提高控制性能，修正航向偏差，得到无人机飞行姿态控制的航向扩展角度修正扫描的等高线，如图2所示。

以此为基础，实现无人机在大迎角飞行下的姿态跟踪控制。为了对比算法性能，采用方位估计方法，进行控制性能测试。文中算法和传统算法下的估计结果如图3所示。

从图中可见，采用文中方法进行无人机大迎角飞行姿态控制，能有效实现对偏航的修正，方位估计的精度较高，收敛性较好。

图2 偏航修正的等高线分布

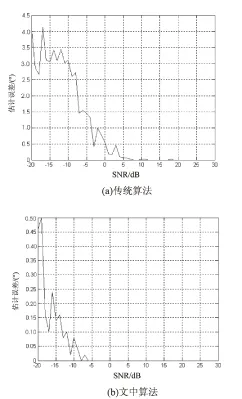
图3 控制性能对比

4 结束语

通过飞机惯导优化控制设计，进行扰动抑制，防止飞机翻滚和失衡，提出一种采用波束域加权谱峰搜索方法进行误差补偿和自适应控制的无人机大迎角飞行姿态控制算法。构建了无人机大迎角飞行的运动数学模型，采用波束域加权谱峰搜索方法构建无人机大迎角飞行的自适应跟踪控制器，实现控制算法改进。研究结果表明，该算法能有效实现对偏航的修正，控制精度较好，收敛性和鲁棒性较传统方法优越。

[1] 宋申民，郭 永，李学辉.航天器姿态跟踪有限时间饱和控制[J].控制与决策,2015,30(11):2004-2008.

[2] 孙克辉,贺少波,董燕青.简化洛伦兹混沌系统的追踪同步控制[J].信息与控制,2015,44(4):393-397.

[3] 李贵明,刘良栋.刚体卫星姿态的有限时间控制[J].空间控制技术与应用,2011,37(3):1-8.

[4] Pratt R W.Flight control systems practicalissues in design and implementation[M].United Kingdom:The Institution of Electrical Engineers,2000:44-49.

[5] Mahboubi H,Moezzi K,Aghdam A G,et al.Distributed deployment algorithms for improved coverage in a network of wireless mobile sensors[J].IEEE Transactions on Industrial Informatics,2011,10(1):1244-1249.

[6] Matheny M H,Grau M,Villanueva L G,et al.Phase synchronization of two anharmonic nanomechanical oscillators[J].Physical Review Letters,2014,112(1):461-467.

[7] 曹美会,鲜 斌,张 旭,等.基于视觉的四旋翼无人机自主定位与控制系统[J].信息与控制,2015,44(2):190-196.

[8] Cabecinhas D，Cunha R，Silvestre C.A nonlinear quadrotor trajectory tracking controller with disturbance rejection[J].Control Engineering Practice,2014,26(1):560-565.

[9] Palomares I,Martinez L,Herrera F.A consensus model to detect and manage non-cooperative behaviors in large scale group decision making[J].IEEE Transactions on Fuzzy System,2014,22(3):516-530.

[10] Weiss S,Achtelik M W,Lynen S,et al.Monocular vision for long-term micro aerial vehicle state estimation:a compendium[J].Journal of Field Robotics,2013,30(5):803-831.

[11] 张 冀,徐科军.自动生成转速参考曲线的电动执行器定位方法[J].电子测量与仪器学报,2014,28(11):1222-1234.

[12] 梁国龙,韩 博,范 展.近场自适应波束形成的零陷展宽方法[J].华中科技大学学报:自然科学版,2013,41(8):34-39.

[13] 何淼磊,贺继林,周烜亦.小型无人直升机鲁棒飞行控制[J].机器人,2016,38(3):337-342.

[14] 李永锋,张国良,王 蜂,等.基于快速视觉里程计和大回环局部优化模型的改进VSLAM算法[J].机器人,2015,37(5):557-565.

High Angle of Attack Flight Attitude Control Algorithm Based on Beam Domain Weighting

LU Xing-hua

(Huali College of Guangdong University of Technology，Guangzhou 511325，China)

When UAV flies in the violent attitude angle changes,large attack angle of extreme flight conditions,parameters change continuously in finite linear model,which brings the uncertainty of system parameters and enlarges the difficulty of flight attitude control.A new algorithm of high angle of attack flying attitude control is proposed based on the weighted spectral peak search method of the beam domain for the error compensation and adaptive control.Construction of UAV in pitch,yaw and roll flight state equations of motion,the beam space weighted spectral peak searching methods are applied to constantly measure the system parameters.According to the attitude parameter measurement,the model is modified,improving of the control performance,correction of the heading error.After constant optimal self regression and least squares fitting,optimal output attitude angle,yaw correction and error compensation is achieved.The simulation results show that using the algorithm to control the high angle of attack flying attitude,its yaw correction and error compensation performance is better,and the robustness and convergence of it are better.

UAV;adaptive control;error compensation;beam domain weighting

2016-01-31

2016-05-11

时间：2017-01-04

广东省2015年教育重点平台及科研项目青年创新人才类项目(自然科学类)(2015KQNCX218)

陆兴华(1981-)，男，硕士，讲师，研究方向为计算机控制算法、嵌入式技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1023.036.html

TP276

A

1673-629X(2017)01-0117-04

10.3969/j.issn.1673-629X.2017.01.026