基于块旋转和清晰度的图像超分辨率重建算法

尧潞阳，解 凯，李 桐

(北京印刷学院 信息工程学院，北京 102600)

基于块旋转和清晰度的图像超分辨率重建算法

尧潞阳，解 凯，李 桐

(北京印刷学院 信息工程学院，北京 102600)

针对传统基于学习的超分辨率重建算法训练时间过长，且对训练库依赖性大的不足，提出一种结合块旋转和清晰度的超分辨率重建方法。该方法引入了一种新的分类机制。为增加训练样本块的多样性，但又不增加计算复杂度，将样本块进行一定角度的旋转，然后引入块清晰度(Sharpness Measure,SM)对训练样本进行分类。对于块清晰度较高的纹理、角以及边缘块，利用分类好的对应样本库进行自相似性重建，而清晰度较低的块，则直接使用插值放大进行重建。在搜索匹配过程中改用Fast Library for Approximate Nearest Neighbors (FLANN)替代传统的Approximate Nearest Neighbors (ANN)搜索，提高了重建效率。最终利用迭代反投影算法和局部约束进行优化。实验结果表明，该算法既可以较大幅度减少计算的复杂度，也能够获得较好的视觉效果。

超分辨率；多尺度自相似性；块旋转；清晰度；迭代反投影；局部约束

0 引 言

从一幅或者多幅低分辨率图像获取高分辨率，即“超分辨率重建”，已经是一个经典问题。高分辨率图像具有低分辨率图像丢失的细节，即高频信息。由于图像的取景和拍照过程中，会存在不可避免的外在干扰，比如光线不足、拍摄抖动等等，将导致获得的图像分辨率较低。尤其在一些特殊领域，如医学中人体内部病理图像的获取，以及高空遥感图像的拍摄，这些都难以通过提高硬件设施来较大幅度地提高图像的分辨率。并且，硬件的成本和工艺制造代价可能远远超出了它所能带来的实际价值，因此，通过数字信号处理或软件算法来提高图像的分辨率已经是当前十分活跃的一个研究领域。

大多数超分辨率算法主要分为以下两种：

(1)经典的基于重建的超分辨率算法：旨在从一系列亚像素偏移的低分辨率图像中重建出原有的高分辨率图像。每一幅低分辨率图像将对高分辨率复原图像进行线性约束，当亚像素位移低分辨率图像足够多时，则足以重建出高分辨率图像[1]。然而这种方法终究逃脱不了经典多幅图像重建的限制。即使图像块充分配准，已滤去足够的噪声，一般也只局限于2倍的分辨率放大[2-3]。

(2)基于学习的超分辨率重建：打破了基于多帧图像重建的约束，采用分块思想，并通过一组有代表性的图像集来学习低分辨率与高分辨率图像块之间的映射关系，利用这种映射关系，估计高频细节，最后预测得到待重建的高分辨率图像。Freeman等[4-5]首次提出了基于学习的超分辨率算法，并且通过Markov网络学习低分辨率图像块与高分辨率图像块之间的映射关系。该方法大量依赖于外界训练库，并且额外的训练库并不一定能保证包含重建所需要的高频细节，容易导致“幻觉”效应[6]。Chang等[7]采用了局部线性嵌入(Local Linear Embedding,LLE)的流行学方法。然而，该方法使用相同的近邻系数线性组合恢复高分辨率块，容易导致欠拟合和过拟合现象。Freedman等[8]在频域中使用基于学习的方法较好地保留了图像边缘。Khatri等[9]针对图像大尺度放大时训练字典过大这一问题，进行筛选简化，剔除相似性大的冗余图像块，大大降低了计算的复杂度。Glasner等[10]结合了传统的和基于学习的超分辨率算法用于单幅图像超分辨率重建，但是实验表明其结合传统多帧重建方法对最终图像的重建质量贡献不大，增加了计算的复杂度，并且其使用的ANN(Approximate Nearest Neighbors)库搜索速度较慢。Singh等[11]针对自相似性难于重建纹理较复杂的图像这一缺点，提出了利用可控金字塔模型将低分辨率输入图像进行多频带分解，然后针对每一频带进行自相似性重建，最后再逆变换回高分辨率图像。

文中对Glasner等的重建过程进行改进，利用图像子块在不同尺度间存在的重复性来学习高低分辨率图像子块之间的映射关系，不需要额外的样例图像库。在样本库生成的过程中，利用块旋转策略[12]，增加块的多样性。并且，针对传统遍历式搜索的缺点，使用块清晰度(Sharpness Measure,SM)[13-14]对样本块进行分类,并针对性地进行重建。实验结果表明，由于进行了分类搜索，重建的每一图像块更具针对性，重建图像得到了更好的视觉效果，并且峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)也得到了相应的提高。

1 图像自相似性及块旋转策略

1.1 基于中频和高频下的多尺度自相似性模型

Glasner等[10]通过对大量自然图像进行测试，得出结论：自然图像都倾向于包含重复性的视觉内容，不论是在同尺度之间，还是不同尺度之间。对于更小的图像块(例如5×5大小)往往在同一图像中会出现更多的块冗余。

以往的自相似性重建几乎都是基于低频和高频，认为低频和高频块之间存在高度相关。然而实验表明这种假设具有内容特定性，针对自然图像中一些纹理较复杂的图像，低频和高频块表现出的相关性较低。因此，在中频块和高频块具有较高相关度下，文中结合多尺度自相似性原理来预测低分辨率图像丢失的高频细节。

1.2 块旋转策略及训练样本库的生成

传统的基于学习的重建方法中，往往都选取大量的外在训练样本来保证重建图像的质量。但是，大量的样本块无疑增加了计算的复杂度，而且通过搜索匹配得到的高频细节块存在多对一的现象，即有可能不是重建最终需要的高频细节，容易导致重建的结果出现“伪影”现象。针对这一缺点，文中在块多尺度自相似性原理的基础上对样本块进行旋转来增加图像样本的多样性，减少了对外在训练库的依赖性。

为保证样本的多样性及计算效率，只对图像进行90°旋转处理。旋转之后，将这些图像块划归到同一个尺度，并对这些块做列向量处理。虽然这些图像块在内容上是相同的，但是，进行列向量处理之后，相同的内容就有了不同的表现形式，得到的训练样本具有多样性，这样可以更加充分地利用图像多尺度自相似性。

为了更好地预测高频信息，首先对低分辨率输入图像I0进行高斯低通滤波和下采样操作，得到多尺度的下采样图像I-1,I-2,…,I-n(n=2)。得到的高斯金字塔由-nth到0th层(最大尺度层，即I0)组成，记第i层为Ii，可得：

(1)

其中，D表示用高斯低通滤波器进行平滑和下采样操作。

为了将对应的Ii分别分解为低频成分Li和高频成分Hi，对式(1)金字塔结构中的每一层图像先按超分辨率放大因子k进行下采样和平滑滤波，然后再插值放大k倍恢复到原图像大小，这样便得到对应的低频成分Li，可由式(2)表示：

Li=U(D(Ii)),-n≤i≤0

(2)

其中，D操作和式(1)中一样；U表示双三次插值操作。

得到了对应的低频成分Li后，将其与对应的图层Ii进行差值即可得到高频成分Hi，如式(3)所示：

Hi=Li-Ii,-n≤i≤0

(3)

然而，式(2)中的低频成分可以进一步分解为低频和高频成分。从第一层低频成分Li中再次抽取出的低频成分称为中频信息，如下：

Mi=Li-U(D(Li)),-n≤i≤0

(4)

得到中频和高频训练图像库后，分别对两个训练库中的每一张图像先进行90°旋转，然后再依次对原图和旋转后的图像进行分块处理。分块原则为：从左往右，从上往下，块大小为5×5,块像素重叠个数为3。最后将每一图像分块后得到的图像块进行累加，分别得到中频图像样本训练块和高频样本训练块对。

2 文中算法

尽管文中搜索重建过程使用FLANN库来替代Glasner等的ANN搜索库，提升了重建时间，效率也更高，但使用FLANN库进行搜索仍然是对全部的训练块进行全局搜索，缺乏针对性。为使得重建的块质量更好，更具针对性，引入块清晰度作为新的分类准则。

2.1 块边缘清晰度的尺度不变性以及样本块分类

Yeganli等[15]对图像块清晰度进行了分类测试，证明了块清晰度具有近似尺度不变性。SM可由梯度幅值表示。对于任意给定的图像块，SM可定义如下：

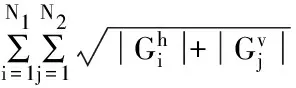
(5)

(6)

(7)

其中，I表示图像像素值。

根据上述公式，图像块的SM值可作为将图像块分类为边缘，角以及纹理块的标准。分类准则如下：

(8)

文中先将下采样得到的中频训练块根据式(8)进行预分类。实验中对N1,N2,N3进行了大量测试，发现分别取值为12,24,40时效果较好。然后将低分辨率输入图像插值到预放大尺度后分块，对于任一待重建的图像块，先求出其SM值，然后根据式(8)判断其属于哪一个区间段，根据其所处的类别进行相应的重建。对于处于第一类(lable1)的图像块，由于其纹理细节较少，则可直接使用插值放大进行重建。然而对于处于其他类型的图像块，含有的细节较丰富，在对应的已分类好的训练样本块中进行自相似性搜索。这种有针对性的训练重建，不仅减少了重建可能带来的误匹配现象，同时缩小了搜索范围，降低了训练的复杂度，可使最终重建的图像视觉效果更好。

2.2 算法整体流程

在实验过程中，为不增加计算复杂度，只进行两个尺度的下采样，即下采样因子a=1.41。

具体算法如下:

(1)将低分辨率输入图像进行多尺度模糊下采样，然后利用块旋转策略旋转后，产生对应的中频和高频样本库。

(2)将待重建的低分辨率图像插值到预放大尺度后进行分块。分块准则为：从上到下，从左到右，大小为5×5，像素重叠个数为3。

(3)计算每一图像低分辨率块的SM值，根据SM值选择相应的重建方式。属于第一类的图像块，直接插值放大，保留当前块。剩下的图像块，在对应训练好的中频样本块中利用FLANN库加速搜索9个最相似的中频块。

(4)利用中频块和高频块对应的映射关系，在高频样本库中找到对应的高频块，然后利用高斯加权分别为不同相似度的图像块赋予不同的权值，最终得到当前低分辨率块需要的高频细节。

(5)将重建的所有高频细节块按照像素重复个数进行加权平均融合，然后加上低分辨率输入图像的插值放大图像可得到初始高分辨率图像。

(6)为使重建的图像更加清晰，避免重建图像与原低分辨率图像偏差过大，使用迭代反投影和局部约束对初始高分辨率图像进行约束和优化。

3 图像后处理

为进一步提高重建图像的分辨率，利用局部约束[16-17]和迭代反投影算法[18]对重建结果进行后处理。

3.1 局部约束

事物是普遍联系的。自然图像也一样，图像中每一个点都是与周围的像素有关联的，共同组成了具有某种结构的图像。自然图像一般具有丰富的信息，包含一些相关联的信息，或者说是冗余信息。而且，具有相关性的像素不仅仅是在邻域内才具有，这种相关性可以扩散到整幅图像。

局部约束的核心是基于图像块的方式对任一图像块进行相似性搜索，寻找周围相似的块，并且利用不同的权值进行加权，最终得到的图形块把图像的全局相似性联系起来，可使得最后的重建图像轮廓更加精准清晰。

对于每一个图像块取5×5大小，以中心像素点为起始在其周围进行相似块筛选，通过事先设置的阈值，计算相似块之间的欧氏距离，如下所示:

(9)

实验中筛选8块最相似的图像块，通过线性加权得到最后的图像块，线性表达如下：

(10)

(11)

(12)

其中，wi为加权权值系数；ck为权重归一化因子；h为控制权值随欧氏距离增加的下降速度(实验中取10)。

3.2 全局约束

为确保每次重建的高分辨率图像与低分辨率输入图像保持一致，针对每一级重建图像进行迭代反投影(IBP)全局优化：

Xt+1=Xt+((Y-DXt)↑)*GuassLowFliter

(13)

其中，Xt+1为第t+1次迭代得到的高分辨率图像；D为降采样因子；↑为放大倍数；GuassLowFliter为高斯低通滤波器。

实验中通过设定一定的迭代次数(由于收敛较快，一般设置为20)，不断更新，以有效防止差错的扩散。

4 实验结果与分析

为验证算法的可行性，分别与双三次插值放大、Chang[7]的基于局部线性嵌入的重建方法和Glasner[10]的自相似性算法进行对比。实验中设置放大倍数为2，块的大小为5×5，旋转角度为90°，FLANN近邻搜索的相似块个数为9，图像下采样尺度为1.41，金字塔层数为2,局部约束中threshold阈值为0.5，h为10，迭代反投影算法迭代次数为20。

对于彩色图像的超分辨率重建，由于人的视觉对光最为敏感，故实验中先将RGB彩色图像转换为YCbCr编码方式,并且只对亮度通道进行，而剩下的cb、cr通道使用Matlab内置的Bicubic插值放大函数进行超分辨率重建。

为进一步客观评价重建后图像的质量，采用峰值信噪比(PSNR)和结构相似性(SSIM)作为评价高分辨率性能的指标，分别对5幅典型的大小为128×128的低分辨率彩色图像进行测试。图1(a)～(e)分别列出了实验中5幅低分辨率图像。

图2列举了其中3幅低分辨率图像两倍放大后对比的效果。表1列出了各算法对比后的PSNR与SSIM值，以及平均提高的数值。

从图2可知，Bicubic插值产生的图像过于模糊和平滑，视觉效果最差。Chang[7]的LLE算法产生的视觉效果比起Bicubic插值有所提高，但也存在过度平滑现象。Glasner[10]的自相似性算法重建出的效果得到了较大程度的提高，但是仍然略有缺陷，即局部边缘不够平滑，存在一定的锯齿和伪影现象。而文中算法重建的效果都优于前三者，由于采用分类训练，针对不同的图像块类进行相对应的重建，更好地保持了图像细节信息，不仅提高了图像重建的效率，也降低了局部块效应和伪影效应。

图1 低分辨率测试图

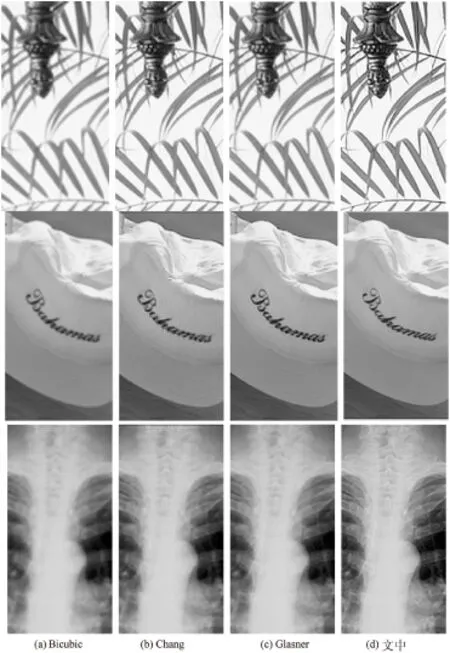
图2 重建结果对比

图像类型BicubicChangGlasner文中算法leaves25．254/0．92328．067/0．95229．271/0．96630．289/0．984parrots30．132/0．93032．028/0．94032．402/0．94832．657/0．952chest41．521/0．97041．505/0．96543．059/0．97843．268/0．982women31．271/0．87232．335/0．88932．541/0．89232．741/0．911hat30．089/0．88130．040/0．87831．988/0．91432．438/0．942平均31．653/0．91332．795/0．92433．852/0．93934．278/0．954

5 结束语

文中在Glasner提出算法的基础上进行了改进，省略了同尺度间多帧重建的步骤，在图像多尺度自相似性原理上结合块旋转策略和块清晰度对低分辨率图像块进行针对性重建。为预测更多的高频细节，改用中频块去预测高频块，然后使用更快的FLANN搜索库替代传统的ANN搜索，提高了自相似性重建图像的质量和效率。实验结果表明，该重建算法能够减少重构图像在某些轮廓部分产生的一些不规则边缘和锯齿效应，重建图像拥有更丰富的细节和更高的峰值信噪比。

[1]TsaiR,HuangT.Multiframeimagerestorationandregistration[J].AdvancesinComputerVisionandImageProcessing,1984,1:317-339.

[2]BakerS,KanadeT.Limitsonsuper-resolutionandhowtobreakthem[C]//ProceedingsofIEEEconferenceoncomputervisionandpatternrecognition.[s.l.]:IEEE,2000:372-379.

[3]LinZ,ShumHY.Fundamentallimitsofreconstruction-basedsuper-resolutionalgorithmsunderlocaltranslation[J].IEEETrans.onPAMI,2004,26(1):83-97.

[4]FreemanWT,PazstorEC,CarmichaelOT.Learninglow-levelvision[J].InternationalJournalofComputerVision,2000,40(1):25-47.

[5]FreemanWT,JonesTR,PasztorEC.Examplebasedsuper-resolution[J].IEEEComputerGraphicsandApplications,2002,22(3):56-65.

[6]BakerS,KanadeT.Hallucinatingfaces[C]//IEEEinternationalconferenceonautomaticfaceandgesturerecognition.[s.l.]:IEEEComputerSociety,2000:83.

[7]ChangH,YeungDY,XiongY.Super-resolutionthroughneighborembedding[C]//ProceedingsofCVPR.[s.l.]:[s.n.],2004:275-282.

[8]FreedmanG,FattalR.Imageandvideoupscalingfromlocalself-examples[J].ACMTransactionsonGraphics,2011,30(2):474-484.

[9]KhatriN,JoshiMV.Efficientself-learningforsingleimageupsampling[C]//22ndinternationalconferenceinCentralEuropeoncomputergraphics,visualizationandcomputervision.[s.l.]:EurographicsAssociation,2014:1-8.

[10]GlasnerD,BagonS,IraniM.Super-resolutionfromasingleimage[C]//Proceedingsofcomputervision.[s.l.]:IEEE,2009:349-356.

[11]SinghA,AhujaN.Super-resolutionusingsub-bandself-similarity[C]//ACCV2014.[s.l.]:SpringerInternationalPublishing,2014:552-568.

[12]XiaJingman,LiWei,TangJie,etal.Imagesuperresolutionbasedonpatchrotationandsparserepresentation[J].OpenJournalofNatureScience,2015,3(2):15266.

[13]GonzalezRC,WoodsRE.Digitalimageprocessing[M].2nded.EnglewoodCliffs,NJ:Prentice-Hall,Inc.,2002.

[14]KumarJ,ChenF,DoermannD.Sharpnessestimationfordocumentandsceneimages[C]//Internationalconferenceonpatternrecognition.[s.l.]:IEEE,2012:3292-3295.

[15]YeganliF,NazzalM,UnalM,etal.Imagesuper-resolutionviasparserepresentationovermultiplelearneddictionariesbasedonedgesharpness[J].SignalImage&VideoProcessing,2016,10(3):535-542.

[16]BuadesA,CollB,MorelJM.Non-localimageandmoviedenoising[J].InternationalJournalofComputerVision,2008,76(2):123-139.

[17]DongW,ZhangL,ShiG,etal.Imagedeblurringandsuper-resolutionbyadaptivesparsedomainselectionandadaptiveregularization[J].IEEETransactionsonImageProcessing,2011,20(7):1838-1857.

[18]IraniM,PelegS.Improvingresolutionbyimageregistration[J].CVGIPGraphicalModels&ImageProcessing,1991,53(3):231-239.

An Image Super Resolution Reconstruction Algorithm Based on Patch Rotation and Sharpness

YAO Lu-yang，XIE Kai，LI Tong

(School of Information Engineering,Beijing Institute of Graphic Communication, Beijing 102600,China)

To address the shortcomings of long-time training and relying on the additional training databases in conventional example-based super-resolution algorithm,a super-resolution image reconstruction algorithm based on patch rotation and sharpness is proposed,which introduces a new classification mechanism.To increase the diversity of training sample patches but not the computational complexity,they are rotated by a certain angle and then introduced the patch Sharpness Measure (SM) to classify the training samples.For patches of high SM,such as textures,corners and edges,the self-similarity reconstruction is carried on by classified samples.For patches of low SM,the interpolation is used directly to enlarge the image for reconstruction.During the searching and matching process,the Fast Library for Approximate Nearest Neighbors (FLANN) to replace the traditional Approximate Nearest Neighbors (ANN) increases the reconstruction efficiency.Finally,iterative back projection and local constraint are used for optimization.Experimental results validate that the algorithm not only can reduce the computational complexity effectively but also achieve better visual effects.

super resolution;multi-scale self-similarity;patch rotation;sharpness measure;iterative back projection;local constraint

2016-03-28

2016-07-05

时间：2017-01-04

国家自然科学基金资助项目(61472036)

尧潞阳(1992-)，男，硕士，研究方向为图像处理与模式识别；解 凯，教授，博士，研究方向为计算机视觉、图像处理与虚拟现实。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1039.078.html

TP301.6

A

1673-629X(2017)01-0070-05

10.3969/j.issn.1673-629X.2017.01.016