新的基于格的可验证加密签名方案

张彦华 胡予濮

(综合业务网理论与关键技术国家重点实验室(西安电子科技大学) 西安 710071) (yhzhangxidian@163.com)

新的基于格的可验证加密签名方案

张彦华 胡予濮

(综合业务网理论与关键技术国家重点实验室(西安电子科技大学) 西安 710071) (yhzhangxidian@163.com)

可验证加密签名(verifiably encrypted signature, VES)能够有效地保证互联网上交易过程的公平性.VES的核心思想是：签名者利用仲裁者的公钥对自己所签发的一个普通数字签名进行加密，随后证明密文中确实包含一个普通签名，任何验证者都可以利用仲裁者的公钥来验证其真实性，但在没有签名者或仲裁者的帮助下无法从中提取出普通签名；当争议发生时，验证者可以要求仲裁者从可验证加密签名中恢复出签名者的普通签名.利用Agrawal等人在美密2010上给出的固定维数的格基委派技术、格上原像抽样算法和差错学习问题的非交互零知识证明，该文构造出一个新的格上可验证加密签名方案，并在随机预言机模型下严格证明了其安全性.与已有的可验证加密签名方案相比，该方案要求签名者根据仲裁者公钥生成签名者公私钥对，构造简单，公私钥和签名尺寸更短，效率更高，并且能够抵抗量子攻击.

可验证加密签名(VES)；固定维数；格；随机预言机模型; 差错学习问题

互联网在线交易已逐渐成为日常生活中比较重要的商品交换方式，如何在分布式网络中保证交换过程的公平性是电子商务安全亟待解决的关键问题之一.1997年，Asokan等人[1]首次提出可验证加密签名(verifiably encrypted signature, VES)的概念.可验证加密签名能够有效地保证互联网上交易过程的公平性.一个可验证加密签名方案包含3个参与者：签名者(又称用户)、验证者和可信第三方(又称仲裁者).VES的核心思想是：签名者利用仲裁者的公钥对自己所签发的一个普通数字签名进行加密，随后证明密文中确实包含一个普通签名，任何验证者都可以利用仲裁者的公钥来验证其真实性，但在没有签名者或仲裁者的帮助下无法从中提取出普通签名；当争议发生时，验证者可以要求仲裁者从可验证加密签名中恢复出签名者的普通签名.

基于双线性Diffie-Hellman假设，Boneh等人[2]于2003年给出了第1个有效的非交互的VES方案.签名验证过程不需要零知识证明，而且方案在随机预言机模型下是可证明安全的.自此以后，VES引起了众多学者的广泛关注，很多基于标准数论假设的VES方案相继被提出[3-7].

近年来，基于格构造新型密码系统因具有较高的渐进效率、运算简单和抗量子攻击等特点，成为后量子时代密码领域的研究热点，并取得了一系列研究成果[8-11].2010年，Rückert等人[12]构造出第1个基于格的标准模型下的VES方案，然而该方案是静态化的.2011年，Wang等人[13]构造出第1个基于格的随机预言机模型下非静态化的VES方案，然而该方案不满足强不可伪造性.2014年，Kim等人[14]构造出一个高效的基于格的VES方案，该方案不再额外需要梅克尔树(Merkle trees)，但是签名者的公私钥尺寸和可验证加密签名的尺寸都明显较大.

本文增添仲裁者密钥生成阶段来生成仲裁者公私钥，并利用Agrawal等人[15]提出的固定维数的格基委派技术来生成签名者密钥，从而有效地减小签名者的公私钥尺寸；然后运用原像抽样算法和差错学习问题(learning with errors, LWE) 的非交互零知识证明构造出一个新的格上可验证加密签名方案，并在随机预言机模型下严格证明了其安全性.与已有的基于格的可验证加密签名方案相比，该方案构造简单，公私钥和签名尺寸更短，效率更高.

1 基础知识

1.1 格

定义1. 设b1,b2,…,bm是n上m个线性无关的向量，格Λ定义为所有这些向量的整数线性组合构成的集合，即}，其中向量组b1,b2,…,bm构成格Λ的一组基B.

定义2. 设q是一个素数，A∈n×mq，u∈nq，则：

(1)

(2)

定义3. 对任意s>0，定义以向量c为中心，s为参数的格Λ上的离散高斯分布为：

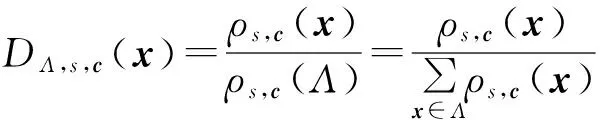
(3)

其中x∈Λ，ρs,c(x)=exp(-π‖x-c‖2s2).

1.2 重要算法

引理1[8]. 设n是正整数，q≥2,m≥2nlbq,对于除了至多2q-n的部分之外所有的A∈n×mq以及任意，向量u=Aemodq的分布统计接近nq上的均匀分布，其中e∈D.

格上陷门抽样算法(TrapGen)、离散高斯抽样算法(SampGau)和原像抽样算法(SampPre)由如下2个引理给出.

引理2[9]. 设n是正整数，q≥2，m>5nlbq,存在概率多项式时间(probabilistic polynomial time, PPT)算法TrapGen(q,n)，输出A∈n×mq和TA∈m×mq，其中A在n×mq上是统计均匀的，TA是格的陷门基，且满足

引理3[8]. 设n是正整数，素数q≥2，m>n，矩阵A∈n×mq.TA∈m×mq是格的陷门基，高斯参数s≥‖‖).对于c∈m和u∈nq，有：

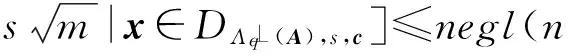
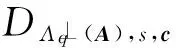
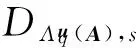
Gordon等人[10]提出了一个变形的格基陷门抽样算法(OrthoSamp)，由如下引理给出.

引理4[10]. 设n是正整数，素数q≥2，正整数m≥n+8nlbq，矩阵B∈n×mq的列向量的子集合构成nq.存在PPT算法OrthoSamp(q,B)，输出矩阵A∈n×mq和TA∈m×mq，使得：

1)ABT=0 modq，其中A的秩为n，且在n×mq上是统计均匀的.

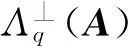
3)TA的任一列向量ti∈mq统计接近，其中).

定义4. 对于矩阵A∈m×m，如果Amodq作为中的矩阵是可逆的，则称A是q可逆的.

Agrawal等人[15]提出的格基委派技术(BasisDel)能够生成固定维数的格基陷门，由如下引理给出.

引理5[15]. 设n是正整数，q>2，m>2nlbq，TA∈是格的陷门基，可逆矩阵R∈Dm×m，高斯参数s≥‖‖m)3.存在PPT算法BasisDel(A,R,TA,s),输出B∈n×mq和TB∈m×mq，其中B=AR-1modq，TB是格的陷门基，且对于参数s的最小值满足‖‖≤‖‖.

引理6[15]. 设n是正整数，q>2，m>2nlbq，矩阵A∈n×mq的列向量的子集合构成nq.存在PPT算法SampRwith(A)，输出矩阵B∈n×mq，R∈m×mq和TB∈m×mq，其中B=AR-1modq，其分布统计接近于Dm×m，矩阵TB∈m×mq是格的陷门基，且满足‖‖).

1.3 格上困难问题

定义6. 小整数解问题(small integer solution, SIS).设n是正整数，q为素数，给定随机矩阵A∈n×mq和实数β=poly(n)，找到非零向量e，使得Ae=0 modq且‖e‖≤β.

定义7. 非齐次小整数解问题(inhomogeneous small integer solution, ISIS).设n是正整数，q为素数，给定矩阵A∈n×mq和向量y∈nq，实数β=poly(n)，找到非零向量e，使得Ae=ymodq且‖e‖≤β.

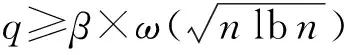
定义8. 差错学习问题(learning with errors, LWE).设n是正整数，q为素数，对任意0<α<1，定义ψα为期望值为0、标准差为α的[0,1)上的正态分布，对应的q上的离散分布为.定义为nq×q上的分布，其中s，ui∈nq是随机选取的向量，xi∈q依分布独立随机选取.LWE问题是指给定As,χ上多项式个样本量，找到向量s∈nq.

1.4 格上非交互零知识证明

2013年，Laguillaumie等人[17]给出了一个满足如下ISIS关系的非交互零知识证明协议，即

RISIS={(A,y,β;x)∈n×mq×nq××m;
Ax=ymodq,‖x‖≤β}.

(4)

利用LWE困难问题与ISIS困难问题的对偶性，Laguillaumie等人同时给出了满足如下LWE关系的一个有效的零知识证明协议，即

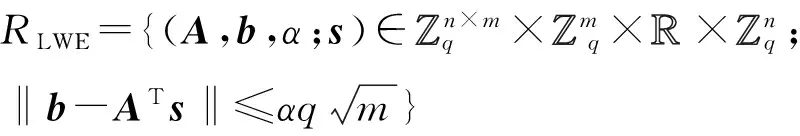
(5)

2 可验证加密签名

2.1 定 义

可验证加密签名由如下8个PPT算法构成.

1) 系统建立(Setup).给定安全参数λ，输出系统公开参数PP.

2) 仲裁者密钥生成(Adj-KeyGen).给定公开参数PP，输出仲裁者公私钥对(APK,ASK).

3) 签名者密钥生成(KeyGen).给定公开参数PP、仲裁者公钥APK，输出签名者公私钥对(PK,SK).

4) 普通签名生成(Sign).给定公开参数PP、私钥SK和消息M，输出普通签名σ.

5) 普通签名验证(Verify).给定公开参数PP、公钥PK、签名σ和消息M，输出接受或拒绝.

6) 可验证加密签名生成(VES-Sign).给定私钥SK、消息M和仲裁者公钥APK，输出可验证加密签名ω.

7) 可验证加密签名验证(VES-Verify).给定公钥PK、APK、签名ω和消息M，输出接受或拒绝.

8) 仲裁(Adj).给定公钥PK、APK、仲裁者私钥ASK、可验证加密签名ω和消息M，输出普通签名σ.

可验证加密签名方案的正确性需满足如下2点：

1) 运用VES-Sign算法生成的可验证加密签名ω必须能通过VES-Verify算法的验证；

2) 仲裁者运用Adj算法可以有效地从可验证加密签名ω中恢复出原始普通签名σ，且σ必能通过Verify算法的验证.

2.2 安全模型

可验证加密签名方案应满足强不可伪造性、强不透明性和可提取性3个安全属性.可通过攻击者与挑战者的交互游戏来定义其安全性.

定义9. 强不可伪造性.若不存在多项式有界的敌手A1能以不可忽略的优势赢得以下游戏，则称一个VES方案是强不可伪造的.

1) 系统建立.挑战者C1输入安全参数λ，运行Setup，Adj-KeyGen和KeyGen算法生成VES方案的公开参数PP和所有公私钥对(APK，ASK)，(PK，SK)，并将(PP,APK,ASK,PK)发送给敌手A1.

2) 询问阶段.A1适应性地进行多项式次如下询问.

① 普通签名生成询问.C1运行Sign算法可获得任何消息M的普通签名σ，并返回给A1.

② 可验证加密签名生成询问.C1运行VES-Sign算法获得任何消息M的VES签名ω，并返回给A1.

3) 伪造阶段.最后，敌手A1输出一个消息M*及其VES签名ω*.

敌手A1赢得上述游戏当且仅当：

1)ω*是消息M*的一个合法VES；

2) (M*,ω*)不是一个可验证加密签名生成的询问结果.

定义10. 强不透明性.若不存在多项式有界的敌手A2能以不可忽略的优势赢得以下游戏，则称一个VES方案是强不透明的.

1) 系统建立.挑战者C2输入安全参数λ，运行Setup，Adj-KeyGen和KeyGen算法生成VES方案的公开参数PP和所有公私钥对(APK，ASK)，(PK，SK)，并将(PP,APK,PK)发送给敌手A2.

2) 询问阶段.A2适应性地进行多项式次如下询问.

① 普通签名生成询问.C2运行Sign算法可获得任何消息M的普通签名σ，并返回给A2.

② 可验证加密签名生成询问.C2运行VES-Sign算法可获得任何消息M的VES签名ω，并返回给A2.

③ 仲裁询问.C2运行Adj算法可获得消息M及其VES签名ω对应的普通签名σ，并返回给A2.

3) 伪造阶段.最后，敌手A2输出一个消息M*及其普通签名σ*.

敌手A2赢得上述游戏当且仅当：

1)σ*是消息M*的一个合法普通签名；

2) (M*,σ*)不是一个仲裁询问结果.

定义11. 可提取性.若不存在多项式有界的敌手A3能以不可忽略的优势赢得以下游戏，则称一个VES方案是可提取的.

1) 系统建立.挑战者C3输入安全参数λ，运行Setup和Adj-KeyGen算法生成VES方案的公开参数PP和所有仲裁者公私钥对(APK，ASK)，并将(PP，APK)发送给敌手A3.

2) 询问阶段.A3适应性地进行多项式次如下询问.

仲裁询问：C3运行Adj算法可获得消息M及其VES签名ω对应的普通签名σ，并返回给A3.

3) 伪造阶段.最后，敌手A3输出一个消息M*及其VES签名ω*，对应的签名者的公钥为PK*.

敌手A3赢得上述游戏当且仅当：

1)ω*是消息M*的一个合法VES；

2)σ*=Adj(PP,ASK,APK,PK*,ω*,M*)不是消息M*的一个合法普通签名.

3 新的基于格的VES方案

3.1 方案构造

1) 系统建立.输入安全参数n，具体参数设置见3.2节.选取2个安全的抗碰撞Hash函数H1:{0,1}*→Dm×m，H2:{0,1}*×mq→nq；输出系统公开参数PP=(n,m,q,s1,s2,s3,α,H1,H2).

2) 仲裁者密钥生成.输入公开参数PP，运行算法TrapGen(q,n)生成随机矩阵B∈n×mq和格的陷门基TB∈m×mq，且‖‖；输出仲裁者公私钥对(APK,ASK)=(B,TB).

3) 签名者密钥生成.输入公开参数PP和仲裁者公钥APK=B；运行算法OrthoSamp(q,B)生成随机矩阵A∈和格的陷门基TA∈，满足ABT=0 modq；输出公私钥对(PK,SK)=(A,TA).

4) 普通签名.输入公开参数PP、私钥SK=TA和消息M，签名者进行如下操作.

① 随机选取比特串r←{0,1}n和向量v∈mq.

② 运行算法SampPre(A,TA,H2(M‖r‖v),s1)，生成向量d∈m.

③ 输出普通签名σ=(M,r,v,d).

6) 可验证加密签名生成.输入公开参数PP、私钥SK=TA、仲裁者公钥APK=B∈n×mq和消息M，签名者进行如下操作.

② 令R=H1(M‖r)，B′=BR-1∈n×mq.

③ 计算v=B′Ts+xmodq，并构造对v的一个有效非交互零知识证明π.

④ 运行SampPre(A,TA,H2(M‖r‖v)-ARTx,s2)生成向量e∈m.

⑤ 输出可验证加密签名ω=(M,r,v,π,e).

7) 可验证加密签名验证.输入签名者公钥PK=A、仲裁者公钥APK=B∈n×mq和签名ω=(M,r,v,π,e)；首先验证非交互零知识证明π的有效性，计算R=H1(M‖r)，如果π是有效的，ABT=0 modq，‖e‖‖r‖v) modq，则接受ω为签名者对消息M的一个有效的可验证加密签名；否则,拒绝.

8) 仲裁.输入签名者公钥PK=A，仲裁者私钥ASK=TB和签名ω=(M,r,v,π,e)，仲裁者进行如下操作.

① 计算R=H1(M‖r).

② 运行算法BasisDel(B,R,TB,s3)生成随机矩阵B′=BR-1∈n×mq和的陷门基TB′∈m×mq.

③ 利用TB′从v=B′Ts+xmodq中解出(s,x).

④ 计算d=e+RTx∈mq.

⑤ 输出普通签名σ=(M,r,v,d).

3.2 参数设置

为保证仲裁过程中可以从v中有效解出(s,x)和系统的安全运行，给定安全参数为n，设置其他参数如下：

m=n+8n1+δ,

(6)

(7)

(8)

(9)

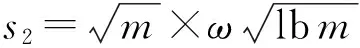
(10)

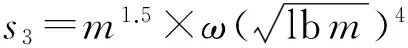
(11)

(12)

3.3 安全性证明

3.3.1 正确性

令ω=(M,r,v,π,e)是可验证加密签名生成算法的一个输出，方案的正确性分析如下：

1) 由于签名者选取随机向量s，从而签名者可以构造出一个有效的非交互零知识证明π.

3) 容易计算Aσ=A(e+RTx)=Ae+ARTx=H2(M‖r‖v) modq.

4) 在可验证加密签名验证算法中，我们有：

A(e+RTv)=Ae+ARTv=Ae+ART(B′Ts+x)=
Ae+A(B′R)Ts+ARTx=Ae+ABTs+ARTx=
A(e+RTx)=H2(M‖r‖v) modq.

3.3.2 强不可伪造性

定理1. 如果存在敌手A1以不可忽略的优势ε1攻破方案的强不可伪造性，则可构造算法B1以概率ε1qH2求解ISIS问题，其中qH2表示敌手可进行H2询问的最大次数.

证明. 假设B1获得了一个ISIS问题实例(A∈n×mq,y∈nq,n,m,q,s)，要求B1通过模拟游戏利用A1求解出一个非零向量e，使得Ae=ymodq且.

模拟过程如下：

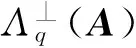
①H1(M‖r‖)询问.B1首先检查列表l1中是否存在对该询问的应答，若存在，直接返回；否则，B1随机选取矩阵R∈Dm×m并将(M,r,R)存储在列表l1中，然后将R返回给A1.

②H2(M‖r‖v)询问.B1首先进行H1(M‖r)询问并获得矩阵R.如果此次询问恰好是第i*次询问，B1计算h2=ARTv+ymodq，并将(M,r,v,h2,⊥)存储在列表l2中，然后将h2返回给A1;如果不是第i*询问，B1计算h2=A(RTv+e) modq，其中e∈D，并将(M,r,v,h2,e)存储在列表l2中，然后将h2返回给A1.

③ 可验证加密签名询问.不失一般性，假设A1在进行可验证加密签名询问之前已进行过H1和H2询问.B1在列表l2中找到(M,r,v,h2,e)，如果e=⊥，则B1直接放弃模拟，否则，返回e作为签名应答.

3) 最终，A1输出一个伪造的可验证加密签名ω*=(M*,r*,v*,π*,e*).不失一般性，假设A1在输出伪造的可验证加密签名之前已经进行过H1和H2询问.B1在列表l2中找到(M*,r*,v*,h,e)，如果e≠⊥，则B1直接放弃，否则，B1直接返回e*作为ISIS实例的应答.

证毕.

3.3.3 强不透明性

定理2. 如果存在敌手A2以不可忽略的优势ε2攻破方案的强不透明性，则可构造算法B2以概率ε2qH1求解LWE问题，其中qH1表示敌手可进行H1询问的最大次数.

模拟过程如下：

1) B2首先构造矩阵B′∈n×mq，其中第i列恰好是向量ui；构造向量v′∈mq，其中第i个分量元素恰好是vi；B2选取随机矩阵R′∈Dm×m，然后运行算法OrthoSamp(q,B′R′)生成随机矩阵A∈n×mq和的陷门基TA∈m×mq，B′R′AT=0 modq；令仲裁者公钥APK=B′R′，签名者公私钥对(PK,SK)=(A,TA)，并将APK，PK发送给敌手A2，同时B2随机选取i*∈{1,2,…,qH1}.B维护3个列表l1，l2，l3分别存储对H1询问、H2询问和可验证加密签名询问的应答.

①H1(M‖r‖)询问.如果此次询问恰好是第i*次询问，B2将(M,r,⊥,R′)存储在列表l1中并将R′返回给A2；如果此次询问不是第i*次询问，B2运行算法SampRwith(B)生成可逆矩阵R∈m×mq，BR-1∈n×mq和TBR-1∈m×mq，B2将(M,r,TBR-1,R)存储在列表l1中并将R返回给A2.

②H2(M‖r‖v)询问.B2首先检查列表l2中是否存在对该询问的应答，若存在，直接返回；否则，B2随机选取向量h2∈nq并将(M,r,v,h2)存储在列表l2中，然后将h2返回给A2.

③ 可验证加密签名询问.不失一般性，假设敌手A2在进行可验证加密签名询问之前已经进行过H1和H2询问.B2在列表l1中找到(M,r,TBR-1,R)，如果TBR-1≠⊥，则B2按照算法步骤进行可验证加密签名生成，否则，令v=v′，B2利用陷门基TA运行算法SampPre(A,TA,H2(M‖r‖v)-AR′Tx,s2)生成向量e,并构造对v的一个有效非交互零知识证明π.B2将(M,r,v,π,e)存储在列表l3中，返回e作为签名应答.

④ 仲裁询问.不失一般性，假设A2在进行仲裁询问之前已经进行过H1询问，当收到A2对可验证加密签名ω=(M,r,v,π,e)的仲裁询问，B2在列表l1中找到(M,r,TBR-1,R)，如果TBR-1=⊥，则B2直接放弃;否则，B2利用TBR-1对v=(BR-1)Ts+xmodq进行求解得x，并返回普通签名σ=(M,r,v,d=e+RTx)给A2，其中R=H1(M‖r‖).

3) 最终，敌手A2输出一个有效的普通数字签名σ*=(M*,r*,v*,d*).在这里，假设σ*是A2从可验证加密签名询问结果中提取出来的.不失一般性，假设敌手A2在输出伪造的可验证加密签名之前已经进行过H1询问、H2询问和可验证加密签名询问.B2首先在列表l1中找到(M*,r*,TBR-1,R)，在列表l3中找到(M*,r*,v,π,e);如果TBR-1≠⊥，则B2直接放弃，否则，我们易知v=v′，R=R′，B2利用R和e可以由向量d*=e+R′Tx求得x，从而可以由v′=B′Ts*+xmodq求解出s*.

因而只要A2成功攻破上述方案的强不透明性，算法B2就可以有效求解LWE问题，从而我们易知算法B2成功求解LWE问题的概率为ε2qH1.

证毕.

3.3.4 可提取性

定理3. 上述可验证加密签名方案满足可提取性.

证明. 对于消息M的VESω=(M,r,v,π,e)，我们证明如果该签名是有效的，那么总可以由ω提取出一个普通签名σ=(M,r,v,d=e+RTx).非交互零知识证明π可以有效确保v=(BR-1)Ts+xmodq中的x是一个短向量.由仲裁过程可知，可以以极大概率从v中提取出x，从而可以构造出短向量d=e+RTx.

由可验证加密签名验证过程可知，

H2(M‖r‖v)=A(e+RTv)=
A[e+RT(BR-1)Ts+RTx]=
A[e+BTs+RTx]=A(e+RTx).

因而只要可验证加密签名ω是有效的，那么v中肯定含有短向量x,使得

A(e+RTx)=H2(M‖r‖v).

证毕.

3.4 效率比较

表1给出了该文方案与已有的基于格的可验证加密签名方案的比较结果.文献[13]的方案仅满足存在性不可伪造性，文献[14]的方案虽满足强不可伪造性(strong unfrogeability)，但签名者的公私钥和可验证加密签名尺寸都明显较大.该文方案虽然要求签名者公私钥对需根据仲裁者公钥生成，但是其构造简单，不仅满足强不可伪造性和强不透明性，而且签名者公私钥和可验证加密签名更短，效率更高，实用性更强.

Table 1 Efficiency Comparison of Schemes表1 方案的效率对比

4 结束语

本文利用Agrawal等人提出的固定维数的格基委派技术，构造出一个新的格上可验证加密签名方案.在随机预言机模型下证明了方案的安全性是基于格上ISIS和LWE问题，保证了其在量子环境下的安全性.与已有的基于格的可验证加密签名方案相比，该方案构造简单，公私钥和签名尺寸更短，效率更高.

[1]Asokan N, Schunter M, Waidner M. Optimistic protocols for fair exchange[C] //Proc of the 4th ACM Conf on Information Security and Privacy. New York: ACM, 1997: 7-17

[2]Boneh D, Gentry C, Lynn B, et al.. Aggregate and verifiably encrypted signatures from bilinear maps[G] //LNCS 2656: Proc of Eurocrypt 2003. Berlin: Springer, 2003: 416-432

[3]Zhou Yousheng, Sun Yanbin, Qing Sihan, et al. An efficient id-based verifiably encrypted signature scheme[J]. Journal of Computer Research and Development, 2011, 48(8): 1350-1356 (in Chinese)(周由胜, 孙艳宾, 卿斯汉, 等. 一种高效的基于身份的可验证加密签名方案[J]. 计算机研究与发展, 2011, 48(8): 1350-1356)

[4]Shen Jian, Wang Jin, Zheng Yuhui, et al. A novel verifiably encrypted signature from weil pairing[C] //Proc of HumanCom and EMC 2013. Berlin: Springer, 2014: 603-607

[5]Calderon T, Meiklejohn S, Shacham H, et al. Rethinking verifiably encrypted signatures: A gap in functionality and potential solutions[G] //LNCS 8366: Proc of CT-RSA 2014. Berlin: Springer, 2014: 349-366

[6]Shim K A. On the security of verifiably encrypted signature schemes in a multi-user setting[J]. Annals of Telecommuni-cations, 2014, 69(11): 585-591

[7]Nishimaki R, Xagawa K. Verifiably encrypted signatures with short keys based on the decisional linear problem and obfuscation for encrypted VES[J]. Designs, Codes and Cryptography, 2015, 77(1): 61-98

[8]Gentry C, Peikert C, Vaikuntanathan V. How to use a short basis: Trapdoors for hard lattice and new cryptographic constructions[C] //Proc of the 40th Annual Symp on Theory of Computing. New York: ACM, 2008: 197-206

[9]Alwen J, Peikert C. Generating shorter bases for hard random lattices[J]. Theory of Computing Systems, 2011, 48(3): 535-553

[10]Gordon S D, Katz J, Vaikuntanathan V. A group signature scheme from lattice assumptions[G] //LNCS 6477: Proc of Asiacrypt 2010, Berlin: Springer, 2010: 395-412

[11]Nguyen P Q, Zhang J, Zhang Z F. Simpler efficient group signatures from lattices[G] //LNCS 9020: Proc of PKC 2015. Berlin: Springer, 2015: 401-426

[12]Rückert M, Schneider M, Schröoder D. Generic constructions for verifiably encrypted signatures without random oracles or NIZKs[G] //LNCS 6123: Proc of ACNS 2010. Berlin: Springer, 2010: 22-25

[13]Wang Fenghe, Hu Yupu, Wang Chunxiao. A verifiably encrypted signature scheme from lattice assumption[J]. Journal of Information and Computational Science, 2011, 8(8): 1431-1438

[14]Kim K S, Jeong I R. Efficient verifiably encrypted signatures from lattices[J]. International Journal of Information Security, 2014, 13(4): 305-314

[15]Agrawal S, Boneh D, Boyen X. Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE[G] //LNCS 6223: Proc of Crypto 2010. Berlin: Springer, 2010: 98-115

[16]Regev O. On lattices, learning with errors, random linear codes, and cryptography[C] //Proc of the 37th Annual Symp on Theory of Computing. New York: ACM, 2005: 84-93

[17]Laguillaumie F, Langois A, Libert B, et al. Lattice-based group signature scheme with logarithmic signature size[G] //LNCS 6477: Proc of Asiacrypt 2013. Berlin: Springer, 2013: 41-61

Zhang Yanhua, born in 1989. PhD candidate in Xidian University. His research interests include public key cryptography based on lattice and provable security.

Hu Yupu, born in 1955. Professor and PhD supervisor. His main research interests include multilinear map, public key cryptography based on lattice, witness encryption and fully homomorphic encryption.

A New Verifiably Encrypted Signature Scheme from Lattices

Zhang Yanhua and Hu Yupu

(StateKeyLaboratoryofIntegratedServiceNetworks(XidianUniversity),Xi’an710071)

Verifiably encrypted signatures (VES) can ensure the fairness of the Internet exchange process effectively. In a VES system, a signer can generate an ordinary signature on a given message using the secret key of the signer and then encrypt it under the public key of the adjudicator. A verifier should be able to verify that this encrypted signature is indeed an encryption of the ordinary signature of the signer, but the verifier cannot be able to extract the ordinary signature. The ordinary signature can only be recovered by the adjudicator from this encrypted signature. Using the technique of basis delegation in fixed dimension suggested by Agrawal et al in CPYPTO 2010, the lattice-based preimage sampling algorithm and a non-interactive zero-knowledge proof for the learning with errors (LWE) problem, this paper constructs a new verifiably encrypted signature scheme from lattices, and based on the hardness of the short integer solution (SIS) problem and the LWE problem, this proposed construction is provably strong unforgeable in the random oracle model. Compared with current verifiably encrypted signature schemes, this scheme needs that the public-private key pair of the signer should be generated according to the public key of the adjudicator, and this scheme can resist quantum attacks and enjoy simpler constructions, shorter public-private keys, smaller signature size and higher efficiency.

verifiably encrypted signature (VES); fixed dimension; lattice; random oracle model; the learning with errors

2015-09-30；

2016-05-16

国家自然科学基金项目(61472309) This work was supported by the National Natural Science Foundation of China (61472309).

TP309