一种基于时延约束的社会网络信用分布优化模型

邓晓衡 曹德娟 潘 琰 沈海澜 陈志刚

1(中南大学信息科学与工程学院 长沙 410083)2 (中南大学软件学院 长沙 410075) (dxh@csu.edu.cn)

一种基于时延约束的社会网络信用分布优化模型

邓晓衡1曹德娟1潘 琰1沈海澜1陈志刚2

1(中南大学信息科学与工程学院 长沙 410083)2(中南大学软件学院 长沙 410075) (dxh@csu.edu.cn)

基于时延约束的影响力最大化问题(influence maximization with time-delay constraint, IMTC)定义为在时延约束条件下，选取网络中一部分初始用户，使得影响力传播过程结束后网络中被成功影响的用户数量最多.现有研究工作主要依据网络结构优化影响力传播模型，或改进启发式算法提高初始节点的选取质量，影响力传播过程中的时间延迟特性及时延约束条件往往被忽略.针对这点不足，基于时延约束的信用分布模型(credit distribution with time-delay constraint model, CDTC)综合考虑见面概率和条件激活概率对信用分配进行优化定义，同时将相邻节点之间不断见面并激活对信用分配的阻碍作用映射到传播增量路径中，最后根据信用分布函数，使用基于时延约束的贪心算法GA-TC，递归选取边际收益最大的节点组成初始节点集合.实验结果表明：在CDTC模型上使用GA-TC算法不仅能够保证初始节点的选取质量，而且具有更高的执行效率及更好的行为执行预测能力.

社会网络；影响力最大化；时延约束；信用分布；贪心算法

互联网的发展不仅为我们带来了生活上的便捷，而且使我们交流与沟通方式产生了巨大的变化.随着越来越多的人使用诸如移动终端等更加便捷的数据交换设备，我们交友与分享智慧的途径变得更加丰富多样，社会结构变得更加复杂，人与人之间的联系也变得更加紧密.一般情况下，通过在线社会网络中用户之间的联系，信息可以以极快的速度和极小的代价进行传播.正因为如此，影响力在社会网络中的扩散和传播为病毒式营销带来了前所未有的机遇和挑战，如何找到初始用户群体使得信息最终的影响传播范围最大已成为热点研究领域之一.

总体看来，在社会网络中对影响力传播进行有效评估面临3个主要问题[1-3]:1)如何评估节点影响力，或者通过何种方式表现影响力的大小;2)如何描述和建模影响力传播过程，使得它能够真实有效地反映影响力传播情况;3)结合给定的影响力传播模型，怎样设计算法对初始节点进行高效且准确的选取.

在社会网络中，用户之间的影响力通过口碑效应进行传播，商家首先找寻初始用户，并利用病毒式营销策略对网络中的群体用户进行产品推广以达到最优化宣传的目的，如何有效准确地鉴别出初始用户是影响力最大化问题(influence maximization, IM)的核心.Domingos 和 Richardson[4-5]首先提出使用优化算法解决影响力最大化问题.Kempe等人[6]将问题公式化表示，并且将它作为离散优化问题进行解决.此外，他们还提出2个影响力传播模型，即独立级联模型(independent cascade model, IC)和线性阈值模型(linear threshold model, LT)，并证明影响力最大化问题是NP难问题.更重要的是，在这2个模型上使用贪心算法能够得到相比于最优解(1-1e)更高的运算结果准确率.然而，IC和LT等模型也存在缺陷，它们需要使用大量的Monto-Carlo模拟来保证对传播结果评估的精确性.该过程需要花费大量的时间，从而使得模型并不普遍适用于解决大型网络的影响力最大化问题.因此，如何寻找具有高效、普适和可扩展性的算法成为亟待解决的问题[7].当前例如LDAG[8]和PMIA[9-10]等启发式算法虽然克服了运算效率低下的问题，但相比于传统贪心算法，启发式算法往往以牺牲计算结果的精确性和稳定性来获取运算效率的提高.除此之外，在现实场景中，经营者会对影响力在网络中传播的过程设置一定的前提，或者对影响力的传播结果限制一定的约束条件[11]，例如，社会网络中的话题的关注与谈论热度会随着时间的推移呈现衰减的特性，在影响力传播的同时，商家往往追求的是在一段时期或者一定传播代价范围内影响力传播覆盖范围的最大化.本文针对时延约束的影响力最大化问题进行研究，已知节点之间的见面事件是它们发生影响作用的前提必要条件，并且1个节点在同一时刻只能和一个出邻居节点发生碰面并尝试激活.我们将见面概率与条件激活概率两者综合考虑，并将其优化应用在影响力的评估和传播过程之中.

针对IM问题，其他一些学者也已经提出了许多有意义的工作.文献[12]提出一种基于用户推荐的方式构建用户之间连接的算法，社交服务运营商通过分时分步向申请者提供推荐名单，使目标用户接受申请者发起邀请的概率最大.文献[13]提出了一种并行计算的方法，将网络划分为不重合的子图，并从节点的影响力和认知度2方面对节点的影响概率进行评价.文献[14]使用矩阵变换，针对节点之间影响力提出一种线性有界的计算方式，同时对影响力的传播进行建模和描述，并提出2种算法对初始节点进行选取.

我们对信用分布模型(credit distribution, CD)进行优化[15]，提出一种基于时延约束的信用分布模型(credit distribution with time-delay constraint, CDTC)，基于真实用户行为记录，结合见面事件、激活事件以及时延约束条件，追踪并得到不同行为在网络中的传播路径，然后对路径中的用户节点逆向分配代表影响力大小的信用值，除此之外，我们根据见面概率和条件激活概率以及影响力随时间衰减的特性对行为传播路径中相邻用户节点之间分配的直接信用进行优化定义.例如，在网络中，节点u和节点v是相邻的2个用户节点，通过分析行为a的传播路径，已知节点v首先执行了该行为，节点u在之后的某时刻也同样执行了行为a，说明在节点u执行行为a的时刻，节点v尝试与节点u碰面并激活成功，这时对节点v分配一个信用值，代表节点v影响节点u的影响力的大小.明显地，如果节点v对节点u的影响力越大，则相应分配给节点v的信用值也就越高，代表节点u对节点v的信任程度越大.在模型中，采用级联的方式对信用度进行分配，即如果节点v并不是行为a的初始执行者，那么我们也会对行为a先于节点v的前一步执行者分配一定的信用让其影响节点u.这里还需要注意的是，对信用的分配需要限定在时延约束条件指定的范围之内.最后，我们在CDTC模型上提出基于时延约束的贪心算法(greedy algorithm based on time-delay constraint, GA-TC)进行近似求解，通过k次迭代，每次选取边际收益最大的节点作为当前轮次最具影响力的初始节点，算法运行结束后得到初始节点集合S.我们工作的主要贡献如下：

1) 对传统信用分布模型CD进行优化并提出时延约束的信用分布模型CDTC，通过结合见面事件和激活事件对影响力在现实社会网络中传播的时间延迟特性进行模拟，并结合影响力随时间衰减的特性对相邻节点之间的信用分配进行优化定义；

2) 提出一个基于时延约束的贪心算法GA-TC，并提出传播增量路径PIP，结合时延约束条件限定信用在网络中的分配范围；除此之外，我们证明了相比于最优解，在CDTC模型中使用GA-TC算法对初始节点选取结果的准确率下限为(1-1e)；

3) 使用真实的社会网络数据集对模型和算法进行模拟和测试，实验结果表明我们提出的方法能够更加真实可靠地反映影响力的传播，并且执行效率明显优于传统算法；在行为影响力的预测方面，CDTC模型上的预测准确度相比于传统信用分布模型有一定的优化和提升.

1 时延约束的影响力最大化

在社会网络中，用户节点之间的信息交换受到时延约束条件的制约，而这种制约表现在时间和空间2方面.对于在线社会网络，用户之间信息交换的空间限制条件被极大地削弱，也正是由于信息交换平台的这种广泛而便捷的特性，使得用户在在线社会网络中交友和信息共享的范围被极大地扩充，与此同时带来的是用户之间关系的脆弱性和易失性.虽然在线社会网络极大地降低了信息在用户之间传递的限制，扩充了信息传播的范围，并提高了信息传递的时效性，但用户对行为的执行仍然存在时间延迟效应，正如用户行为日志中记录的相同行为被不同执行者执行的时间间隔并不确定且存在差异一样，行为在网络中传播同样受到时间延迟的影响.例如社交网络服务用户只有看到消息提醒并在打开终端后才会看到好友发来的消息，也只有这个会面过程之后其他用户对他的影响才会生效，这里我们引入1个随机变量，定义为见面事件，并将后续的影响激活事件发生的概率看作是见面事件发生前提下的条件概率.对于影响力最大化问题IM，传统的定义方式被描述为在网络中找寻k个初始用户节点，使得在影响力传播过程结束后，网络中被初始节点集合S激活的节点的个数最大(如算法1所示).

算法1. 传统贪心算法.

输入：用户关系图G=(V,E)，初始集合大小k，影响力传播模型M；

输出：初始节点集合S.

①S←∅;

② fori=1→kdo

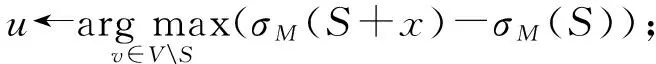
④S←S∪{x};

⑤ end for

⑥ returnS.

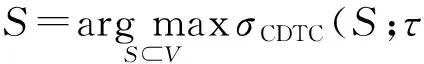
2 时延约束的信用分布模型

2.1 事件概率与模型性质

一般情况下，社会网络可以构造为一个无向图G=(V,E)，其中V表示网络中的用户集合，E代表不同个体之间的关系，S代表初始节点集合.在独立级联模型(IC)中，随着影响力的传播，网络中相邻节点之间会产生一次性的激活尝试，并且随机选取范围(0,1)之间的值作为节点之间的激活概率(在计算时一般根据节点的度值定义)，每个被激活的节点在当前时刻变为激活状态，同时会对其他所有处于未激活状态的出邻居节点产生一次性的激活尝试，且次序随机，尝试成功的节点会在下一时刻执行和父节点相同的行为步骤[16].其中影响者的影响力施加行为和被影响者的被激活行为我们认定为是瞬时且不可逆的，除了行为的初始执行者，被激活者总可以找到1个且唯一的影响成功施加者.在线性阈值模型(LT)中，邻居节点施加的影响力可以累积，并通过网络中每个节点的阈值来体现节点对于当前信息的偏好程度.具体过程如下，假设当前时刻为t，t>0，对于网络中某个节点u(u∉St，St为时刻t网络中已经被激活的节点集合)，当其所有处于激活状态的入邻居节点对其影响力之和大于自身阈值时，节点u在时刻t+1被激活且保持激活状态，同时对所有未激活的出邻居节点产生影响.此外，IC和LT模型都需要对节点影响力的影响范围进行定义，我们用参数X来表示影响力传播路径形成的影响力传播范围可行域.对于一个带权有向图G=(V,E,p)，给定的影响力传播模型M，影响力传播函数σM(S)可以写为：

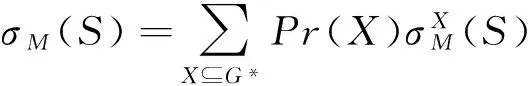
(1)

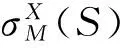
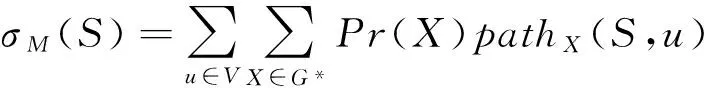
(2)

根据期望的定义重写式(2)，得：

(3)

式(3)表明影响力传播函数σM(S)等于每个节点u∈V被初始节点集合S激活的概率之和.在时延约束的信用分布模型CDTC中，我们用信用分布过程结束后积累在节点上的信用值来表示节点的影响力.同时，我们使用用户行为日志中记录的真实行为传播路径对Pr(path(S,u)=1)进行直接评估，也就是说，我们针对不同的行为，统计并追踪用户在不同时刻执行的情况，生成行为传播路径(action propagation path, APP).因为传播的时间延迟效应，相邻节点只有在见面的前提下才会产生影响作用，加入时延约束条件τ，信用的分布被限定在一定的范围之内，最终提高计算的效率.需要注意的是，因为行为执行的时序性，我们假定同一个用户对相同的行为最多只能执行1次，而且并不是在一个节点受到影响并被成功激活后就立即对相邻的节点产生影响，而是在双方发生见面并尝试激活后，被影响的用户节点才会执行相同的行为，因此，对于同一个行为的传播路径构成的图是一个有向无环图DAG.在影响力传播范围评估方面，我们在模型中使用信用分布函数σCDTC(S)代替影响力传播函数σM(S)，即给定集合S，让其影响网络中其他节点的总信用.

假设图中存在一条行为传播路径P={v1,v2,v3,…,vn}，其中相邻节点之间的边(vi,vj)∈P，则这条链路的激活概率为：

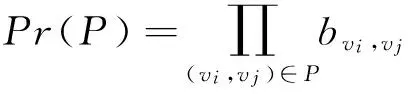
(4)

加入见面概率m后，相邻节点vi和vj之间的激活概率为bvi,vj.设网络中相邻节点vi和vj发生见面的事件用A表示，事件B表示节点vi已处于激活状态且vi将vj成功激活，则有如下定理：

定理1. 网络中相邻节点vi和vj之间发生见面的概率为m，见面条件下vi将vj成功激活的条件概率为α，则用户节点vj被节点vi激活成功的概率bvi,vj=mα.

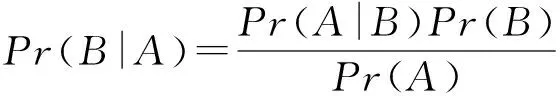
证毕.

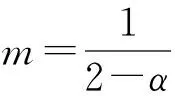
证明. 由贝叶斯定理可得

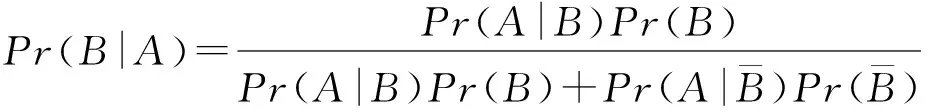
因为条件概率Pr(A|B)=1，所以可以得到

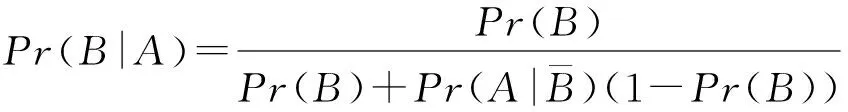
综合考虑这2种情况，假设见面概率m为未知参数，则似然函数可以表示为：

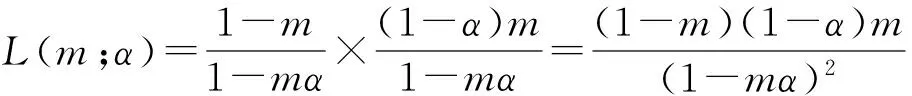
(5)

取对数似然函数，将其转化为：

L(m;α)=lg(1-m)+lg(1-α)+
lgm-2lg(1-mα).

(6)

对式(6)取关于参数m的梯度，可以得到：

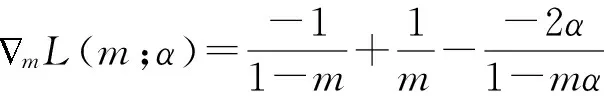
(7)

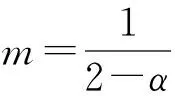
证毕.

在CD模型中，相邻节点之间的影响力使用的是节点度值定义方式，即γvi,vj=1|Nout(vi)|.在本文中，根据推论1中见面概率和见面条件下的激活概率之间的优化关系，并结合定理1，当给定节点之间见面条件下的激活概率α时，可以得到网络中任意节点vj被其邻居节点vi激活成功的概率为bvi,vj=.一般情况下，相邻节点之间条件激活概率α的值参照节点度值的倒数定义，即对于节点u，在见面条件下被邻居节点激活的概率为，其中Nin(u)代表节点u的入邻居节点集合.然而，当节点的入度为0时，概率公式的分母为0，计算失效.因此，我们采用Laplace平滑方法对上述概率计算公式进行改进，在分母中加入平滑因子c，同时分子加1，则计算公式变形为.

类似于网络中热点话题的传播会随着人们关注度的降低而逐渐减弱，节点之间的影响力也会随着时间的推移而递减.我们使用函数sigmoid对影响力进行平滑衰减变换，模拟影响力的衰减特性，并以此作为相邻节点之间分配直接影响力的依据，即分配给vi对其影响出邻居vj的直接信用定义为

(8)

其中tvi(a)和tvj(a)分别代表vi和vj执行行为a的时刻.二者之间的时间跨度越大，表明分配给的信用越小，vi对vj的影响力也就越弱.

定理2. 社会网络中相邻用户节点之间加入见面概率后，使用时延约束的信用分布模型CDTC，信用分布函数仍然具有单调性和子模特性.

证明. 在模型中，当相邻节点之间的见面概率m=1时，见面事件变为必然事件，此时时延约束的信用分布模型CDTC等价于传统信用分布模型CD.由于尝试见面和激活而使行为传播路径增长为传播增量路径，设2个节点集合S和T，S⊆T，虽然时延约束条件τ将信用分布限制在一定范围之内，但是明显有σCDTC(S)<σCDTC(T)，即信用分布函数σCDTC(S)为单调递增函数.

根据CDTC模型的定义可知，模型通过对信用的分配和积累来表现不同节点的影响力大小，所以对于信用分布函数子模特性的证明可以转化为证明给予集合S让其影响节点w的总信用TS,w是否具有相同的性质.以下使用数学归纳法证明，假设在CDTC模型中，TS,w具有子模特性，当前信用分配的路径长度表示为η，时延约束条件为τ.首先考虑当η<τ并且η+1≤τ时，对于任意节点x，x∉T，根据函数的子模特性可得TS+x,w(a;η)-TS,w(a;η)≥TT+x,w(a;η)-TT,w(a;η).当路径长度为η+1时，对于∀u∈V,根据本文2.2节式(12)计算函数的差值

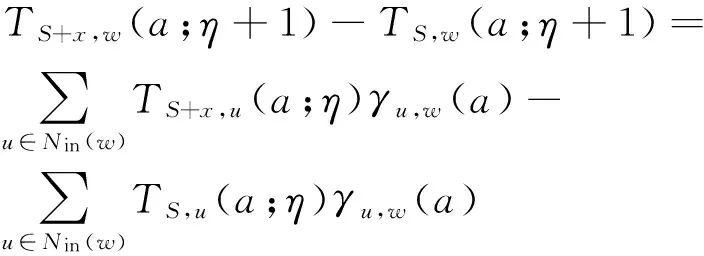
(9)

对式(9)化简并根据题设中的子模特性可得

TS+x,w(a;η+1)-TS,w(a;η+1)≥

将不等式右边展开,即可得到

TS+x,w(a;η+1)-TS,w(a;η+1)≥

TT+x,w(a;η+1)-TT,w(a;η+1)，

所以当信用分配的路径长度为η+1时定理2成立.当η≥τ时，因为信用的分配受到时延约束条件τ的限制，距离过长的节点不再被分配信用，即TS,w(a;η+1)=0，所以上式的左右两边相等.

证毕.

2.2 时延约束条件下的信用分布

社会网络中，用户对于行为的执行记录被保存在用户行为日志中，而对于单个行为的整个执行过程，则是按照时间顺序形成连续的过程记录，用户行为日志中的每条记录可以表示为(u,t,a)，即用户u在时间t执行了行为a.通过对用户行为日志的遍历，并结合用户关系网络，我们可以针对行为得到其被执行的整个过程.同理，假设用户u是用户v的直接出邻居，u∈Nout(v)，用户v在时刻t1执行了行为a，并且用户v与用户u成功见面并尝试激活(在线社会网络中可以理解为用户u看到用户v的消息)，如果用户u在时刻t2(t2>t1)也执行了相同的行为a，则认定在网络中节点v成功见面并激活了节点u.

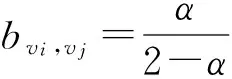
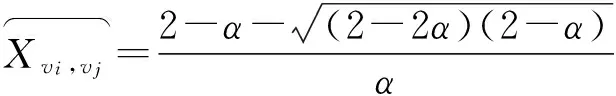
(10)

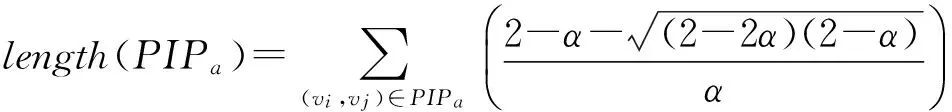
结合用户行为日志和用户之间的关系网络，针对行为得到传播增量路径PIP，之后我们在时延约束条件τ限制的范围内对路径中的节点逆向分配信用，这样节点之间的影响力就可以通过信用分布结束后网络中的每个节点积累的信用值来表示，如果信用值较大，我们认定网络中其他节点对其的信任程度也较高，其反向对他们的影响力也就较大.信用分布的具体过程描述如下：当节点u执行行为a，节点u或者是该行为的初始执行者，或者是被动转发者.执行的同时，节点u会对其他所有没有执行过该行为的邻接节点产生影响.相似地，我们定义如果节点v执行行为a之后，节点v的邻接节点u也执行了行为a，那么给节点v分配信用让节点v影响节点u.对于PIP中任何相邻的2个节点u和v，分配给节点v的信用的大小根据式(8)计算.另外，由于节点之间的信用分配采用类似于影响力级联传播过程的分配方式，所以不仅节点v会被分配信用，节点v之前对于行为a的前任执行者也会被分配信用让其影响节点u，信用的分配范围被限定在τ的范围之内.对于任意的2个节点v和u，给予节点v让其影响节点u的总信用定义为

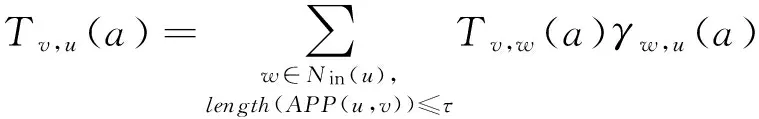
(11)

其中，w为节点u的入邻居，γw,u(a)为给予w让其影响节点u的信用大小.相似地，给予节点集合S让其影响节点u的总信用可以定义为

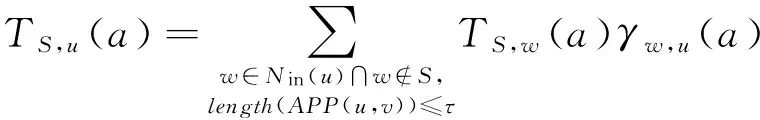
(12)

值得注意的是CDTC模型并不像IC或者LT模型，它是通过学习历史性的行为传播记录来追踪行为传播路径，并依据行为传播路径逆向分配信用值.另外，我们在CDTC模型上选取初始节点并形成初始节点集合S.因为不需要执行任何的Monte-Carlo模拟就可以得到影响力传播结果的准确评估，所以保证了在模型上对最大影响力初始节点选取工作的高效性和可靠性.

3 基于时延约束的贪心算法

3.1 节点边际收益

σCDTC(S+v)-σCDTC(S)=

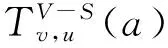
3.2 基于时延约束的贪心算法

现已证明在IC和LT模型中计算初始节点集合影响力传播大小的期望值是NP难问题[6].当前许多启发式算法的提出正是为了近似有效地求解影响力最大化问题，然而在快速得出运算结果的同时它们并不能保证结果的精确性和可靠性.相比之下，因为在CDTC模型中信用分布函数仍然具有单调性和子模特性，所以使用贪心算法计算初始节点可以保证得到精确率相比于最优解下限为(1-1e)的选取结果.算法2给出了基于时延约束的贪心算法GA-TC的具体步骤.

算法2. 基于时延约束的贪心算法.

如算法2所示，我们首先对初始节点集合S和记录节点边际收益的队列Q进行初始化(行①).对网络中的任意节点u，计算节点u与相邻节点w在见面条件下的激活概率α，并根据见面概率m和α之间的优化关系计算节点u成功激活w的概率bu,w(行②～⑤).然后通过遍历训练集用户行为日志，并根据用户关系网络、时延约束条件τ以及行④计算得到节点间的激活概率来构建传播增量路径PIP.同时，依据路径中用户节点之间的激活概率对路径中的相邻节点分配直接信用(行⑥).之后根据信用分布函数的定义σCDTC(S)计算节点的边际收益，排序后插入存储队列Q中(行⑦～⑨).在随后选取初始节点的阶段中，我们需要进行k轮迭代，每轮选出Q中记录的边际收益最大的节点作为当前轮次的候选节点，记为节点x，利用信用分布函数的子模特性，判断当前候选节点x的信用值更新轮次it是否符合当前轮次|S|，若x.it=|S|，则将节点x插入到初始节点集合S中.这里需要注意的是，因为集合S加入了初始节点x，所以我们需要对V-S中节点的信用分布进行更新.若x.it<|S|，则重新计算节点x的边际收益，按更新后值的大小将节点x插入到Q中相应位置，并返回判断循环条件(行⑩～)，算法运行结束时输出初始节点集合S(行).

4 实 验

本节主要对CDTC模型和GA-TC算法的性能与计算结果进行验证.针对不同方法选取的初始节点集合，通过设计对比实验比较影响力传播范围的大小，验证模型和算法对于影响力最大化初始节点选取的有效性和可靠性.同时设计实验对比不同方法在运行时间方面的差异性表现.最后通过设计实验模拟并计算行为日志中测试集行为的真实传播结果，对比于传统信用分布模型比较并判断我们的方法在影响力传播预测方面是否具有更高的准确度.

IC模型相邻节点之间的激活概率通过EM算法学习而来[17]，而LT模型中邻接节点v，u之间的激活概率使用ppv,u=1|Nin(u)|进行计算[14-15]，其中|Nin(u)|表示节点u的入邻居节点个数.对于这2个模型，我们将Monte-Carlo模拟的次数均设定为10 000次.相比之下，在CDTC模型中对于任意节点u，设定u与相邻节点之间见面条件下的激活概率α=c(c+|Nin(u)|)，其中平滑参数c的作用是当c>0时，防止节点入度为0从而分式无意义的情况出现.c值的设定也是有限定性要求的，当c值过大，传播增量路径变小，时延约束条件τ对路径长度的限定作用也会随之减弱.通过实验比较，我们设定c=7，τ=15.相比之下，CD模型仍然使用原始的定义和设计模式[15].

实验环境为2.13 GHz Quad-Core Intel Xeon CPU E5506 8 GB RAM服务器.

Fig. 1 Influence spread consequence based on different models图1 不同的模型对于初始集合的影响力传播

4.1 实验数据集

本文中的实验数据集共2个，均来自SNAP公共数据集.第1个数据集源自图片媒体分享网站Flickr[18]，总数据集包含105938张照片.根据照片的来源共分为4个部分，我们选择其中之一作为实验对象，包含2 602个节点、222 292条边和24 648张照片.处理之后得到2个文件，其中图文件记录网络中用户之间的关联关系，用户行为日志文件包含以时间顺序记录的用户行为.值得注意的是，用户行为日志文件中包含75 269条记录，我们将用户行为记录分成2部分，即包含2 724种行为的训练集用户行为记录和包含1 816种行为的测试集用户行为记录.第2个数据集为High-energy physics citation network[19]，其中包含34 546个节点和421 578条边.我们依据时间排列将不同文章中相同的引用看作是其作者对相同行为的执行过程，以此构建的用户行为日志中包含412 674条记录.

4.2 实验结果与分析

4.2.1 影响力传播

首先在Flickr数据集上使用CDTC模型对问题进行建模，并使用GA-TC算法求解初始节点集合.同理，依次在CD、IC和LT模型上对相同的数据集进行对比实验，对于给定不同的k值，这4种方法得到的影响力传播结果如图1(a)所示.当k=10时，4种方法的初始节点影响力传播结果依次为24.74，29.78，20.87,17.79；当k=50时，4种方法得到的结果依次变为91.63，93.36，84.39，78.69.图1(b)表示初始节点在CDTC模型和CD模型中初始用户的影响力传播结果(信用分布结果)与用户真实影响力之间的差异对比关系.

综合图1可以看出，CDTC模型虽然在影响传播方面略低于CD模型，但是其影响力计算值与真实影响力传播结果之间的误差要明显小于CD模型，并且随着初始节点个数的增加，这种优势呈现增长的趋势.这主要是因为我们在CDTC模型中加入时延约束和时间延迟等现实因素，降低了对于影响力传播结果过于乐观的估计，并使得影响力计算更加真实可靠，保证初始节点选取的质量.而相比于IC和LT模型，CDTC模型的另一个优势在于它是对用户真实的行为记录进行学习，并结合用户特征以及时间特性，而不是仅仅依据网络结构对用户影响力和影响力的传播进行评价，所以我们的方法具有更加真实地反映用户行为和影响力传播的能力.

4.2.2 运行时间

我们首先对Flickr数据集进行测试.如图2(a)所示，当k=50时，在CDTC模型上和在CD模型上对初始节点的选取的运行时间分别记录为 1.96 min，2.19 min，相比之下，在IC和LT模型上的运行时间分别记录为30.98 min，145.82 min.为了便于观察，我们扩大CDTC模型和CD模型选取相同数量初始节点的运行时间的纵坐标范围，运行时间对比结果如图2(b)所示.很明显可以看出，在CDTC模型上选取初始节点在时间消耗方面呈现线性增长趋势，且运行时间少于在CD模型上选取相同数量节点所消耗的时间，随着k值的增加，这种优势更加明显.除了对用户真实行为记录的学习从而避免执行大量且繁重的Monto-Carlo模拟，我们方法的优势还来源于时延约束条件对影响力传播以及等价的信用分配范围的限制作用.相比于CD模型，采用CDTC模型以及GA-TC算法对初始节点的选取工作具有高效性.值得说明的是，IC模型采用了CELF优化策略，所以在时间消耗呈现阶梯式分布；而LT模型则在时间消耗方面呈指数增长的趋势.

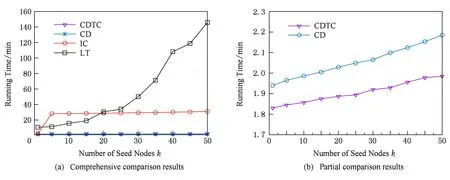
Fig. 2 In Flickr dataset, the running time comparison under different models图2 在Flickr数据集中，不同的模型对于初始节点选取所消耗的运行时间

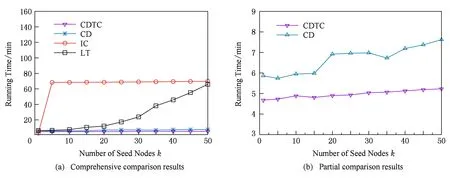
Fig. 3 In HEPC dataset, the running time comparison under different models图3 在HEPC中，不同模型对于初始节点选取所消耗的运行时间

我们同样对HEPC(high-energy physics citation network)数据集进行实验.如图3(a)所示，当k=50时，4种方法对于初始节点选取的时间消耗分别为5.23 min，7.62 min，69.91 min,65.95 min.为了便于观察，图3(b)为缩小纵坐标范围之后2种方法的的对比结果.结合图3可以看出，随着初始节点个数的增加，排除实验结果误差的影响，CDTC模型和CD模型对于初始节点的选取所消耗的时间呈现线性增长的趋势，而LT模型上的时间消耗则呈现指数增长的趋势.不仅如此，在IC模型和LT模型上对初始节点选取所消耗的时间远远大于在CDTC模型上对同等数量节点选取所花费的时间.

综上所述，CDTC模型和GA-TC算法在影响力最大化初始节点选取方面具有高效性.

4.2.3 影响力传播预测

随着商业营销对用户行为分析需求的不断增加，针对特定信息或行为的分析和预测变得越来越有价值.在实验中，我们在Flickr数据集中使用CDTC和CD两种模型对其测试集中记录的行为进行影响力传播预测，测试集包含全部1 816种行为，实验结束后我们按照真实的影响力传播结果对不同的行为进行排序，并将实验预测结果与其真实值进行对比.图4(a)为在CDTC和CD模型上对编号1～1 816行为的影响力传播预测对比结果，以测试集中经过排序后行为编号为602的行为为例，真实的影响力传播大小为8，使用CDTC模型和CD模型对该行为影响力传播的预测值分别为6.76和6.03，同样，以测试集中行为编号为1 727的行为为例，真实的影响力传播大小为60，而使用CDTC模型和CD模型对该行为影响力传播的预测值分别为37.87和35.64.值得注意的是，我们并不是根据某一单一行为进行的影响力传播预测，而是对测试集中1 816种不同的行为分别使用2种模型进行测试，并将预测结果和真实值相比较.根据均平方根误差的计算公式，2种方法得到预测结果的RMSE值分别为17.520 9和18.783 2.由此可见，除去个别噪点样本，CDTC和CD模型对测试集行为样本的影响力传播预测结果均低于真实值；但从统计结果可以看出，相比于CD模型，在CDTC模型上对于用户行为的预测效果有一定程度的优化和提升.图4(b)为对数坐标系中的影响力传播预测对比结果，图中实心圆点近似将空心圈点覆盖，并且趋近于星号点表示的真实值.除此之外，实验结果也表现出在CDTC模型上的影响力传播结果具有无尺度网络节点度分布的幂律分布特性，这也从侧面印证了信用分布过程中用户行为日志和用户关系网络两者结合所发挥的关键性作用.综上所述，实验结果表明我们提出的方法相比于传统信用分布预测方法具有更高的精确度.

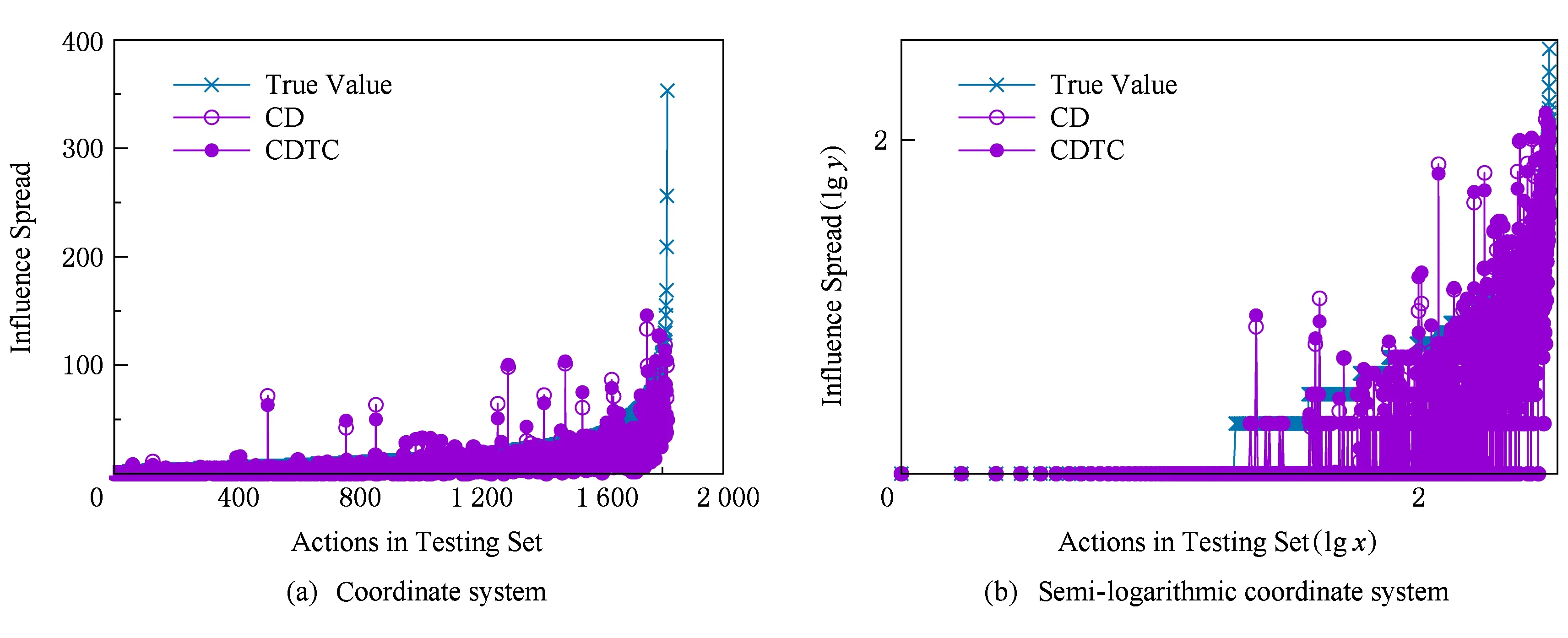
Fig. 4 Influence prediction for user actions图4 用户行为影响力预测

5 结论与展望

本文结合影响力传播过程中存在的时间延迟特性，提出一种基于时延约束的信用分布模型CDTC，并基于该模型提出了基于时延约束的贪心算法GA-TC，近似求解影响力最大化问题.我们综合考虑见面事件和激活事件，将见面概率和见面条件下相邻节点的激活概率进行优化，得出相邻节点之间激活成功的概率，结合影响力随时间衰减的特性，对邻接节点之间信用分配的进行优化定义.除此之外，在行为执行结束后，通过对用户行为日志和用户关系网络结构的学习，将用户之间反复见面并尝试激活对行为传播的阻碍作用投射到传播路径长度的增长方面，提出传播增量路径PIP，同时结合时延约束条件，对路径中的节点逆向分配信用值，这样不仅可以限制信用分布的范围，还可以简化信用分配的计算，提高执行效率.不仅如此，通过学习真实的行为传播记录，我们不需要执行Monte-Carlo模拟就可以实现对影响力传播结果的精确评估，从而大幅度降低了算法的时间复杂度.在影响力传播方面，也正是基于对真实行为传播日志的学习，并加入见面概率、激活概率、衰减特性以及时延约束条件，我们的模型能够更加真实合理地反映用户的行为，保证初始节点选取的质量.实验结果表明在CDTC模型中使用GA-TC算法对初始节点集合的选取工作具有高效性和可靠性.

对于时延约束的影响力最大化问题，还有许多方面可以在未来的工作中做进一步研究.首先，虽然加入见面概率来表现用户延迟接触行为信息影响的可能性，但是并未考虑用户对于信息可能存在的偏好特性.其次，用户的特异性判定也并未加入到其影响力的评估中.我们可以通过学习用户行为日志，对用户的行为习惯以及行为偏好进行分析，并将结果加入到影响力的传播以及信用分布的判定当中.除此之外，我们还可以通过对用户行为标签的学习，更加真实准确地判别用户的行为.在未来的工作中，我们将继续对不同种类的社会网络进行基于主题的影响力挖掘，设计出更加真实有效的影响力传播模型和影响力最大化算法.

[1]Wu Xindong, Li Yi, Li Lei. Influence analysis in online social networks [J]. Chinese Journal of Computers, 2014, 37(4): 735-752 (in Chinese)(吴信东, 李毅, 李磊. 在线社交网络影响力分析[J]. 计算机学报, 2014, 37(4): 735-752)

[2]Xu Ge, Zhang Sai, Chen Hao, et al. Measurement and analysis in online social networks [J]. Chinese Journal of Computers, 2014, 36(1): 165-188 (in Chinese)(徐恪, 张赛, 陈昊, 等. 在线社会网络的测量与分析[J]. 计算机学报, 2014, 36(1): 165-188)

[3]Xiao Tao, Chen Yunfang, Zhang Wei, et al. Review of influence in social networks [J]. Journal of Computer Applications, 2014, 34(4): 980-985 (in Chinese)(夏涛, 陈云芳, 张伟, 等. 社会网络中的影响力综述[J]. 计算机应用, 2014, 34(4): 980-985)

[4]Domingos P, Richardson M. Mining the network value of customers[C] //Proc of the 7th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2001: 57-66

[5]Richardson M, Domingos P. Mining knowledge-sharing sites for viral marketing[C] //Proc of the 8th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2002: 61-70

[6]Kempe D, Kleinberg J, Tardos E. Maximizing the spread of influence through a social network[C] //Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146

[7]Rahimkhani K, Aleahmad A, Rahgozar M, et al. A fast algorithm for finding most influential people based on the linear threshold model [J]. Expert Systems with Applications, 2015, 42(3): 1353-1361

[8]Chen W, Yuan Y, Zhang L. Scalable influence maximization in social networks under the linear threshold model[C] //Proc of 2010 IEEE Int Conf on Data Mining. Piscataway,NJ: IEEE, 2010: 88-97

[9]Chen W, Wang Y, Yang S. Efficient influence maximization in social networks[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 199-207

[10]Chen W, Wang C, Wang Y. Scalable influence maximization for prevalent viral marketing in large-scale social networks[C] // Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 1029-1038

[11]Chen Wei, Lu Wei, Zhang Ning. Time-critical influence maximization in social networks with time-delayed diffusion process [J]. Chinese Journal of Engineering Design, 2012, 19(5): 340-344

[12]Yang D N, Hung H J, Lee W C, et al. Maximizing acceptance probability for active friending in on-line social networks[C] //Proc of the 19th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2013: 713-721

[13]Li H, Bhowmick S S, Sun A. CINEMA: Conformity-aware greedy algorithm for influence maximization in online social networks[C] //Proc of the 16th Int Conf on Extending Database Technology. New York: ACM, 2013: 323-334

[14]Liu Q, Xiang B, Chen E, et al. Influence maximization over large-scale social networks: A bounded linear approach[C] //Proc of the 23rd ACM Int Conf on Information and Knowledge Management. New York: ACM, 2014: 171-180

[15]Goyal A, Bonchi F, Lakshmanan L V S. A data-based approach to social influence maximization [J]. VLDB Endowment, 2011, 5(1): 73-84

[16]Saito K, Nakano R, Kimura M. Prediction of information diffusion probabilities for independent cascade model[C] //Proc of the 12th Int Conf on Knowledge-Based Intelligent Information and Engineering Systems. Berlin: Springer, 2008: 67-75

[17]Goyal A, Bonchi F, Lakshmanan L V S. Learning influence probabilities in social networks[C] //Proc of the 3rd ACM Int Conf on Web Search and Data Mining. New York: ACM, 2015: 241-250

[18]Mcauley J, Leskovec J. Image labeling on a network: Using social-network metadata for image classification [J]. Computer Vision-ECCV, 2012, 7575(1): 828-841

[19]Leskovec J, Kleinberg J, Faloutsos C. Graphs over time: Densification laws, shrinking diameters and possible explanations[C] //Proc of the 11th ACM SIGKDD Int Conf on Knowledge Discovery in Data Mining. New York: ACM, 2005: 177-187

Deng Xiaoheng, born in 1974. Professor and PhD at Central South University. Senior member of CCF. His main research interests include several areas in wireless communications and networking, especially on network transmission and routing optimization with cross-layer design method.

Cao Dejuan, born in 1992. Master candidate in the School of Information and Communication Engineering, Central South University. Her main research interests include influence maximization in social networks and big data analysis (caodejuan@csu.edu.cn).

Pan Yan, born in 1990. Master candidate in the School of Information Science and Engineering, Central South University. His main research interests include influence maximization in social networks (panyan@csu.edu.cn).

Shen Hailan, born in 1974. Received her PhD degree from Central South University in 2011. Currently associate professor at the School of Information Science and Engineering, Central South University. Her main research interests include mobile computing, big data analysis, and oppor-tunistic network (hailansh@csu.edu.cn).

Chen Zhigang, born in 1964. PhD supervisor. Fellow member of CCF. His main research interests include network computing and distributed processing (czg@csu.edu.cn).

An Optimized Credit Distribution Model in Social Networks with Time-Delay Constraint

Deng Xiaoheng1, Cao Dejuan1, Pan Yan1, Shen Hailan1, and Chen Zhigang2

1(SchoolofInformationScienceandEngineering,CentralSouthUniversity,Changsha410083)2(SchoolofSoftware,CentralSouthUniversity,Changsha410075)

The research of influence maximization in social networks is emerging as a promising opportunity for successful viral marketing. Influence maximization with time-delay constraint (IMTC) is to identify a set of initial individuals who will influence others and lead to a maximum value of influence spread consequence under time-delay constraint. Most of the existing models focus on optimizing the simulation consequence of influence spread, and time-delay factors and time-delay constraint are always ignored. The credit distribution with time-delay constraint model (CDTC) incorporates the meeting and activation probabilities to optimize the distribution of credit considering time-delay constraint, and utilizes the optimized relationships of meeting and activation probabilities to evaluate the ability to influence on adjacent individuals. Furthermore, the obstructive effect due to repeated attempts of meeting and activation is reflected by the length of increased propagation paths. After assigning the credit along with the increased propagation paths learned from users’ action-logs, the nodes which obtain maximal marginal gain are selected to form the seed set by the greedy algorithm with time-delay constraint (GA-TC). The experimental results based on real datasets show that the proposed approach is more accurate and efficient compared with other related methods.

social networks; influence maximization; time-delay constraint; credit distribution; greedy algorithm

2015-12-18；

2016-07-05

国家自然科学基金项目(61379058,61272149,61379057,61350011) This work was supported by the National Natural Science Foundation of China (61379058, 61272149, 61379057, 61350011).

TP39