具有并联不等深度子背腔序列的微穿孔板吸声体吸声特性
2017-02-21闵鹤群郭文成
闵鹤群 郭文成
(东南大学建筑学院, 南京210096)(东南大学城市与建筑遗产保护教育部重点实验室, 南京210096)
具有并联不等深度子背腔序列的微穿孔板吸声体吸声特性
闵鹤群 郭文成
(东南大学建筑学院, 南京210096)(东南大学城市与建筑遗产保护教育部重点实验室, 南京210096)
详细讨论了一种新型宽频带微穿孔板(MPP)吸声体的吸声特性,该吸声体由单层MPP和基于二次余数扩散体(QRD)深度序列设计的多个并联且深度不等的子背腔组成.首先,从理论上提出了该吸声体正入射吸声系数的解析计算方法;然后,建立了有限元数值仿真模型验证所提出的解析计算方法,并分析该吸声体的正入射吸声特性;最后,在矩形驻波管内基于传递函数法实验测量了该吸声体样品的正入射吸声系数.实验结果表明,所提出的该类吸声体正入射吸声系数的解析计算方法准确可靠.同时,在460~3 500 Hz的频率范围内,采用解析计算方法预测的该类MPP吸声体的正入射吸声系数不小于0.5,最大吸声系数能达到0.98.
微穿孔板;吸声体;二次余数扩散体;有限元法;实验
微穿孔板(micro-perforated panel, MPP)吸声体具有防潮、耐腐蚀、表面强度高等优点,被广泛应用于对环保和洁净度要求较高的厅堂、医院等场所.MPP吸声体准确的结构设计理论由马大猷先生首创并发展[1-2],它是一种典型的非纤维类吸声体,依靠穿孔直径达到丝米级(0.1~1 mm)的MPP提供良好吸声所需的声阻.如何有效拓展MPP吸声体的吸声带宽一直是研究热点[3-7].马大猷[2]提出使用双层“串联”MPP或者在单层MPP上采用2种直径的穿孔来获得双共振体系,可有效拓展吸声带宽.蔺磊等[7]通过在MPP吸声体背腔中按不同方式填充不同厚度的纤维吸声材料,获得了较宽的有效吸声带宽,但是纤维吸声材料的使用增加了MPP吸声体结构的复杂性,并使其失去了非纤维类吸声体的性能优势.若能在保持优势的前提下,尽可能地拓展吸声带宽,将使MPP吸声体具有更高的应用价值.Wang等[8]提出了一种具有平行排列的3个不等深度背腔的MPP吸声体,并采用有限元仿真和实验的方法对该吸声体的吸声性能进行了研究,结果表明不等深度的背腔与MPP组合产生不同频率的局部共振效应可有效拓展吸声带宽.而平行排列背腔(也称并联排列)的方式比串联背腔的方式,节省了空间且更加经济,在拓展MPP吸声体吸声带宽上具有很大的潜力.但是已有研究中尚缺乏背腔并联MPP吸声体对应的正入射吸声系数的解析计算方法,无法掌握其快速且精确的设计.
另一方面,从Fujiwara等[9-10]首次在混响室中观察到了二次余数扩散体(quadratic residue diffuser, QRD)在低频附近非预期的较高吸声现象以来,越来越多的学者[11-13]开始对QRD潜在吸声能力进行深入的研究.QRD最早是由德国声学家Schroeder[14]在20世纪70年代作为一种高效的声学扩散体设计并提出的,其腔体结构设计基于二次剩余序列排列理论.当声波经过不等深度腔体的反射后,会在QRD的表面形成相位差,进而产生声压差,声压差趋于平衡状态的趋势迫使表面声波产生均衡流动,从而提供了额外的吸声效果,且该吸声效果会在QRD表面附加阻抗单元后得到明显的提高[12].
若借鉴QRD腔体结构来设计MPP吸声体并联式的子背腔,将有可能提升MPP吸声体的吸声性能,但目前尚无这方面的研究报道.本文基于QRD深度序列设计排布了并联不等深子背腔的MPP吸声体结构(简称为QRD-backed MPP吸声体),提出了快速且准确的正入射吸声系数解析计算方法,并分析其正入射吸声特性.
1 理论分析
QRD深度单元序列的计算公式为
(1)
式中,N为QRD的阶数,取质数;x为腔体的序号,取值范围为0~N-1;c为空气中的声速;fr为设计频率.对于7阶QRD,其一个周期的单位深度序列lx为[0,1,4,2,2,4,1],不考虑深度单元为0的腔体,在QRD表面附加MPP后,得到的QRD-backed MPP吸声体的横截面如图1所示.

图1 QRD-backed MPP吸声体2个周期的横截面几何模型
1.1 MPP的相对声阻抗
MPP声阻抗与空气特性阻抗之比称为相对声阻抗,当相对声阻抗在1附近时,可获得理论上的最佳吸声条件.根据马大猷[1]提出的微穿孔板吸声体理论,MPP与空气的相对声阻抗ZMPP为
ZMPP=r+jωm
(2)
(3)
(4)
式中,r为相对声阻;ω=2πf为角频率,f为声音的频率;m为相对声质量;kr和km分别为声阻常数和声质量常数;η为黏滞系数;ρ为空气密度;σ,d和t分别为MPP的穿孔率、穿孔直径和板厚度;k为穿孔常数,可由下式计算:
(5)
1.2 子背腔体内的声能损失
本文研究的QRD腔体的宽度远小于声音的半波长,因此可近似认为声音在腔体中仅以平面波的形式传播.在传播过程中,声波受到腔体壁面导热性和黏滞性的影响,转化为热能被吸收.根据Morse 等[15]提出的理论,腔体中声波传播的波数为
(6)
式中,k0=ω/c为波数;b为腔体的宽度;γ为比热,空气的γ≈1.4;dv和dh分别为腔体内壁黏滞层和热边界层的厚度,可由下式计算:
(7)
(8)
式中,K为导热系数;CP为常压下单位质量的比热.当腔体深度为lx时,其声阻抗率为
(9)
ρe=ρ(1+(1-j)dv/b)
(10)
式中,ρe为腔体中空气的有效密度,故腔体与空气的相对声阻抗为
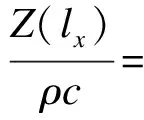
(11)
1.3 QRD-backed MPP吸声体吸声性能解析计算方法
在分别求得MPP和QRD腔体的相对声阻抗后,引入吸声体表面导纳函数G(x),它等于MPP和QRD腔体相对声阻抗之和的倒数,即
(12)|
当声波以θe的角度入射到QRD-backed MPP吸声体表面时,形成入射声场pe(x,z)和扩散声场ps(x,z)[12],即
p(x,z)=pe(x,z)+ps(x,z)
(13)
pe(x,z)=Peej(-kx+zkz)
(14)
式中,Pe为单位声压;kx和kz分别为x方向和z方向的声波波数,即
kx=k0sinθe,kz=k0cosθe
(15)
(16)
式中,An为振幅系数,因为QRD的几何结构是周期性的,所以其表面的扩散声场也是周期性的;βn和γn分别为x方向和z方向的空间谐波波数,即
(17)
(18)
式中,T=(N-1)b为单个周期QRD的宽度;λ=2π/k0为声波波长;n为辐射谐波指数,对于远声场的声波来说,其辐射谐波指数ns应满足以下条件:
(19)
由QRD表面声压和质点速度关系式ρcvz(x,0)=-G(x)p(x,0),可进一步得到
(20)
G(x)是以T为周期的周期性函数,可通过傅里叶分析表示为
(21)
(22)
将方程(21)代入到方程(20)中,等式两边同时乘以ejm(2π/T)x后再从0到T积分可得
m=-∞,…,+∞
(23)
(24)
为了使方程(23)计算结果收敛,n和m的取值范围为[-2N, 2N].综上可计算出振幅系数An,则QRD-backed MPP吸声体的吸声系数为
(25)
2 数值结果与讨论
基于Wang等[8]的有限元模型,本文建立了QRD-backed MPP吸声体的有限元仿真模型对所提出的解析计算方法进行数值验证.数值建模工作借助于有限元分析软件COMSOL Multiphysics进行,其中单个周期的QRD-backed MPP吸声体的有限元网格如图2所示,建模中忽略MPP自身振动带来的影响.
当声音在阻抗管中以平面波的形式正入射时,其入射声压为
pi=exp[j(ωt-k0x)]
(26)
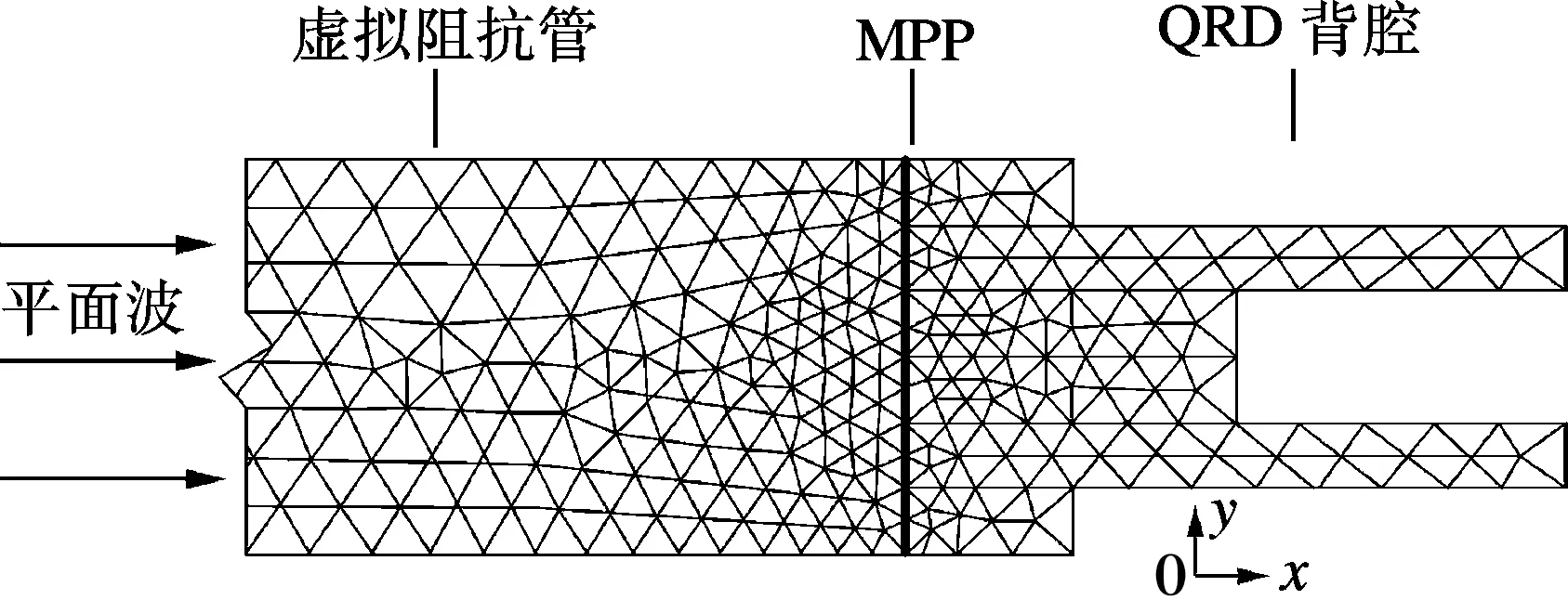
图2 吸声体实例1单个周期的有限元仿真网格化模型
QRD-backed MPP吸声体的有限元仿真模型包括虚拟阻抗管声场区域、MPP声阻抗结构和QRD背腔声场区域,阻抗管内和吸声体背腔的声场由声波方程决定,即
(27)
式中,φ为声场的总速度势,由声场的声压p和质点速度u决定,即
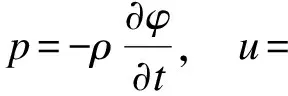
(28)
本文构建了2个数值实例来验证1.3节中提出的吸声体吸声性能解析计算方法.数值实例1中,吸声体背腔的几何结构如图1所示.背腔深度比值l1∶l2∶l3∶l4∶l5∶l6=1∶4∶2∶2∶4∶1,选择设计频率为980 Hz,故所得背腔深度分别为:l1=25 mm,l2=100 mm,l3=50 mm,l4=50 mm,l5=100 mm,l6=25 mm,背腔单位深度为25 mm,宽度均为15 mm.MPP的参数为:板厚t=0.4 mm,穿孔直径d=0.4 mm,穿孔率σ=1.8%.分别使用解析计算方法和有限元仿真对该吸声体的正入射吸声系数进行预测,结果如图3(a)所示.结果表明,2种方法对应的结果能够很好地吻合,初步验证了解析计算方法的准确性和可靠性.同时由图可见,实例1中的吸声体的吸声曲线有一个特点,即在630,900,1 300和1 970 Hz处具有4个明显的共振吸声峰.为分析这些吸声峰的来源,采用Maa[16]提出的单层微穿孔板正入射吸声系数计算方法验算了背腔深度D=25,50和100 mm的单层微穿孔板吸声体的吸声峰,如图3(a)所示.结果显示,实例1的QRD-backed MPP吸声体的各共振吸声峰位置,与3种深度空腔对应的单层微穿孔板吸声体的主共振峰及其谐峰位置基本吻合,略有偏移,且深度越小,偏移越大;同时,虽然实例1的QRD-backed MPP吸声体有6个空腔,但基于经典的QRD背腔深度比值设计为左右对称,2个等深度的子背腔对应的共振吸声峰实际上发生了合并.由图3(a)结果可见,组合后的QRD-backed MPP吸声体的每个共振峰相比对应的单层微穿孔板吸声体的共振峰都略有升高,表明此时不同深度空腔之间的相互耦合共振能提高吸声体整体的吸声能力.这些现象与Wang等[8]的结果一致.
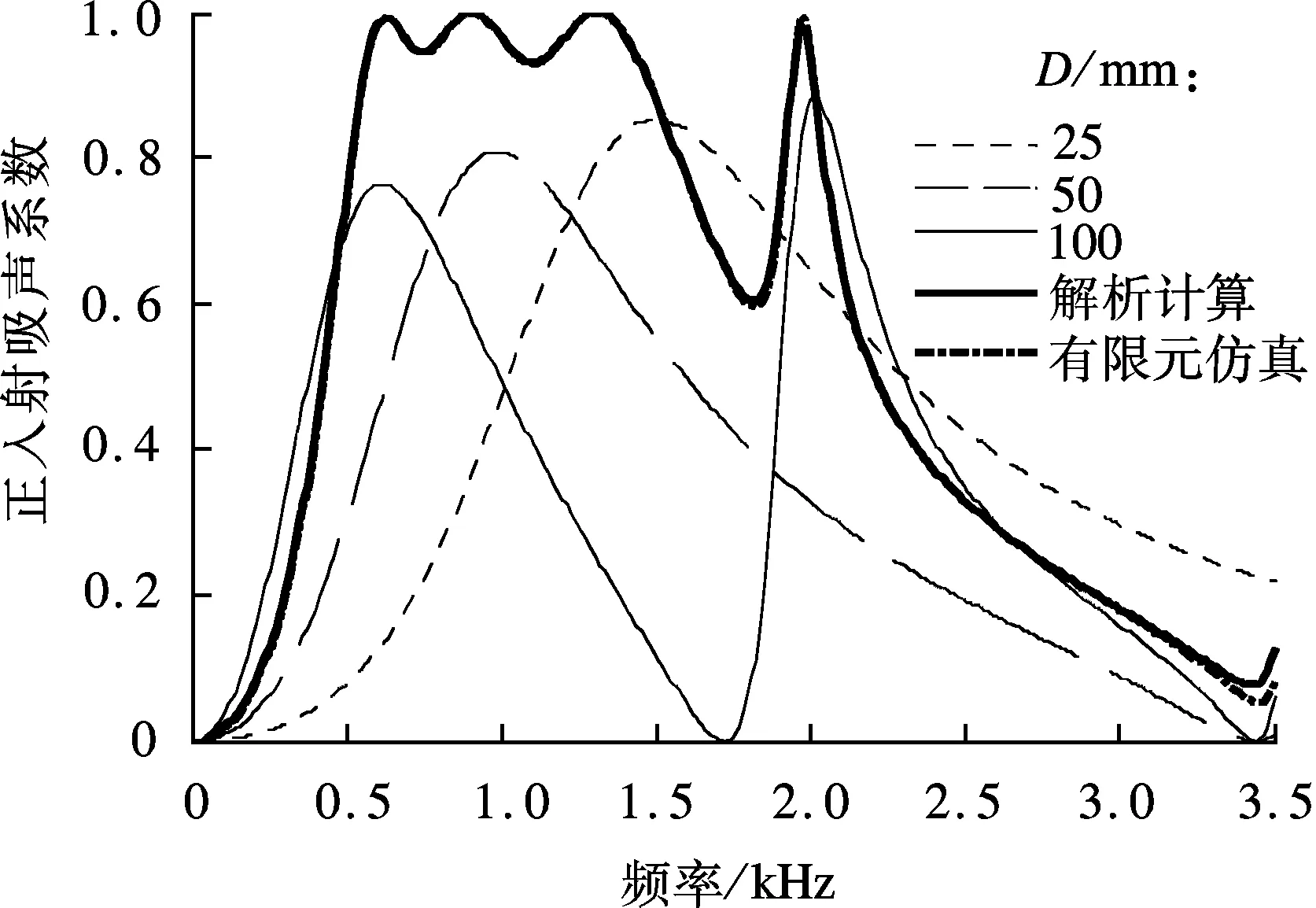
(a) 数值实例1
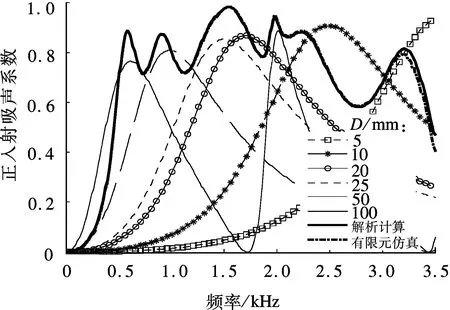
(b) 数值实例2
本文采用数值实例2进一步验证提出的解析计算方法,同时基于实例1中观察的现象进一步拓宽QRD-backed MPP吸声体的吸声频带.实例2中,MPP的参数和背腔的宽度与实例1相同,但空腔深度进行了调整:背腔l1∶l2∶l3=1∶4∶2,背腔单位深度为25 mm;背腔l4∶l5∶l6=2∶4∶1,但单位深度调整为5 mm,即l1=25 mm,l2=100 mm,l3=50 mm,l4=10 mm,l5=20 mm,l6=5 mm.此时QRD-backed MPP吸声体子背腔l1∶l2∶l3∶l4∶l5∶l6=5∶20∶10∶2∶4∶1,已不再是式(1)中的经典QRD的背腔深度比例形式,这样的处理可有效地错开2组空腔对应的共振峰位置.实例2仍分别采用提出的解析计算方法和有限元仿真对QRD-backed MPP吸声体的正入射吸声系数进行预测,结果如图3(b)所示.由图可见,本文所提出的QRD-backed MPP吸声体正入射吸声系数解析计算方法的预测结果与有限元仿真计算结果吻合很好,进一步验证了解析计算方法的准确性和可靠性.该结果同时表明,所提出的解析方法的准确性与QRD-backed MPP吸声体子背腔深度比值是否满足式(1)中的经典QRD排布规律无关.
实例2中的QRD-backed MPP吸声体分别在590,910,1 550,1 980,2 240和3 210 Hz具有了多个共振吸声峰,相比实例1,其吸声频带宽度得到了明显拓展,尤其是频率大于1 980 Hz后的高频段.本文进一步验算了吸声体6个不等深度子背腔所对应的单层MPP吸声体的共振峰位置,吸声曲线见图3(b).可以看到,在2 240和3 210 Hz处的2个高频吸声峰分别与具有10和5 mm深度空腔时的单层MPP吸声体吸声峰偏差较大,且在频率1 550 Hz处的吸声峰很可能是25和20 mm两个不等深空腔对应的共振峰合并而成.为进一步确认吸声峰来源,本文基于有限元仿真模型考察了各吸声峰中心频率附近QRD-backed MPP吸声体内的声强分布情况.如图4所示,当进入某个子背腔的声强变为极大时,该子背腔即与表面MPP发生耦合共振,该部分MPP的吸声将达到极大值.从图4还可看出,实例2中QRD-backed MPP吸声体的各个吸声峰主要来源于各个子背腔的局部共振吸声;当2个子背腔深度相近(如D=20,25mm)时,其共振吸声的频率也相互接近,于是出现吸声频谱上共振峰连续而合并的现象(见图3(b)中1 440~1 550 Hz连续的共振峰).
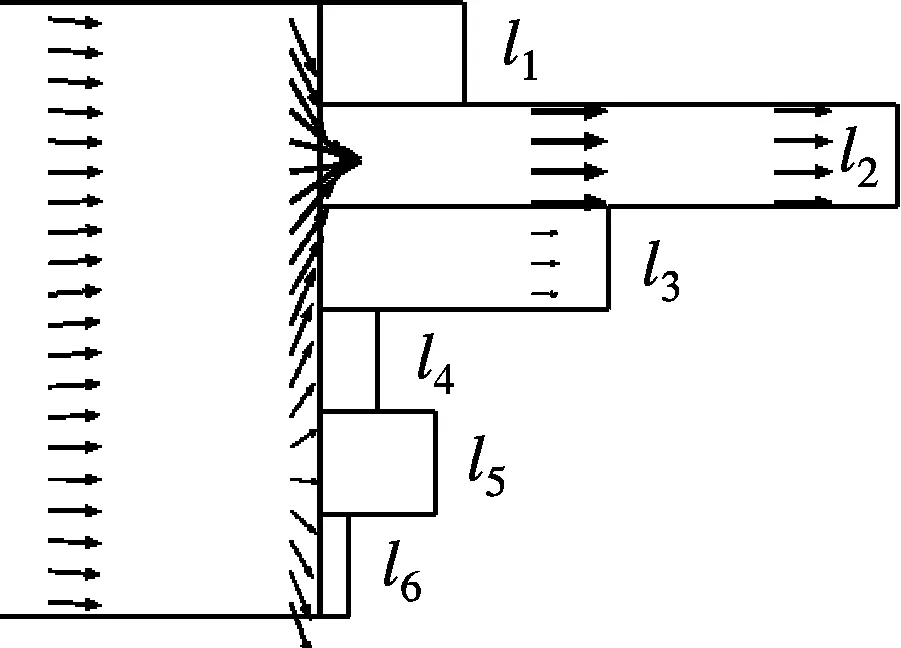
(a) f=590 Hz
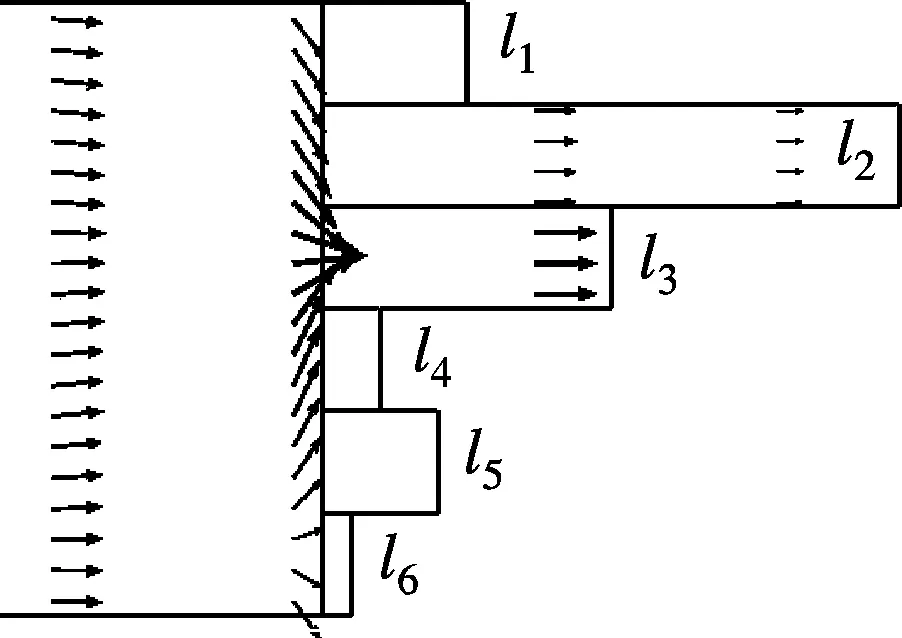
(b) f=910 Hz
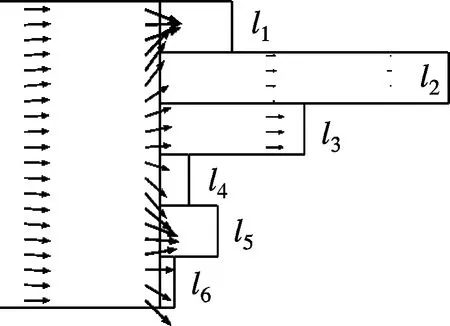
(c) f=1 440 Hz
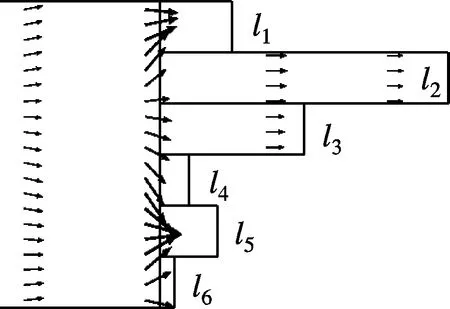
(d) f=1 550 Hz
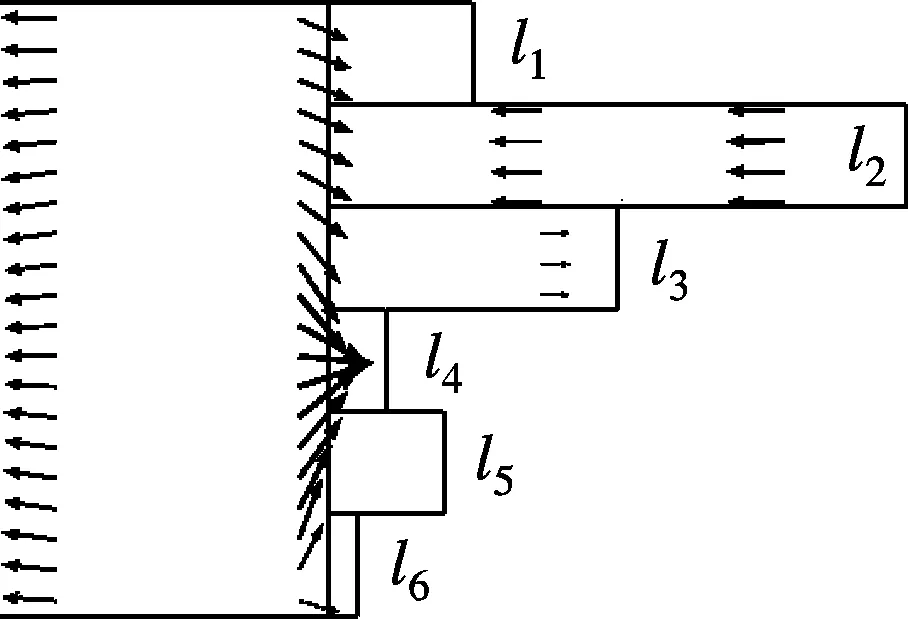
(e) f=2 240 Hz
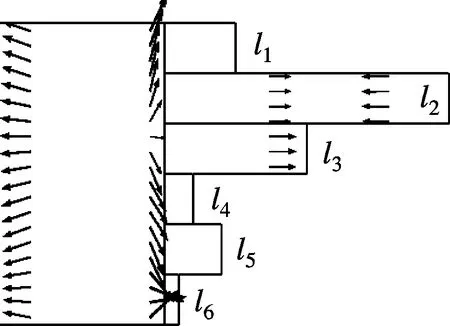
(f) f=3 210 Hz
为了进一步分析并联子背腔MPP吸声体结构的特点,本文采用串联子背腔结构的MPP吸声体的正入射吸声系数进行对比,如图5(a)所示.串联子背腔结构由6层子背腔组成,如图5(b)所示,其深度l1~l6的参数定义与实例2保持一致,每一层MPP的参数均与实例2中MPP参数相同.由图5可见,使用串联子背腔结构后,由于背腔总深度增加,MPP吸声体在更低频获得了相对较好的吸声效果,正入射吸声系数频谱得到了一定程度的扩宽.但与并联子背腔结构的MPP吸声体实例2相比,串联子背腔结构的MPP吸声体在较高频的吸声带宽扩展较差,半吸声频带宽度也相对较窄.此外串联子背腔结构的MPP吸声体在具体应用中劣势明显:① 多个子背腔串联所占空间很大,图5(b)中串联子背腔结构的总背腔深度达到了210 mm,为进一步拓宽吸声频带,所需的总背腔深度将更大;② 串联子背腔结构中每个子背腔表面都需要增加1块MPP,而MPP在实际应用中是吸声体成本的主要部分,这将极大地增加应用成本.
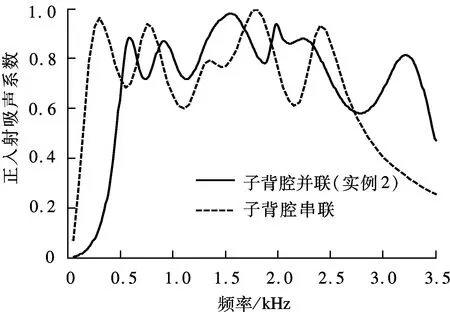
(a) 正入射吸声系数曲线对比
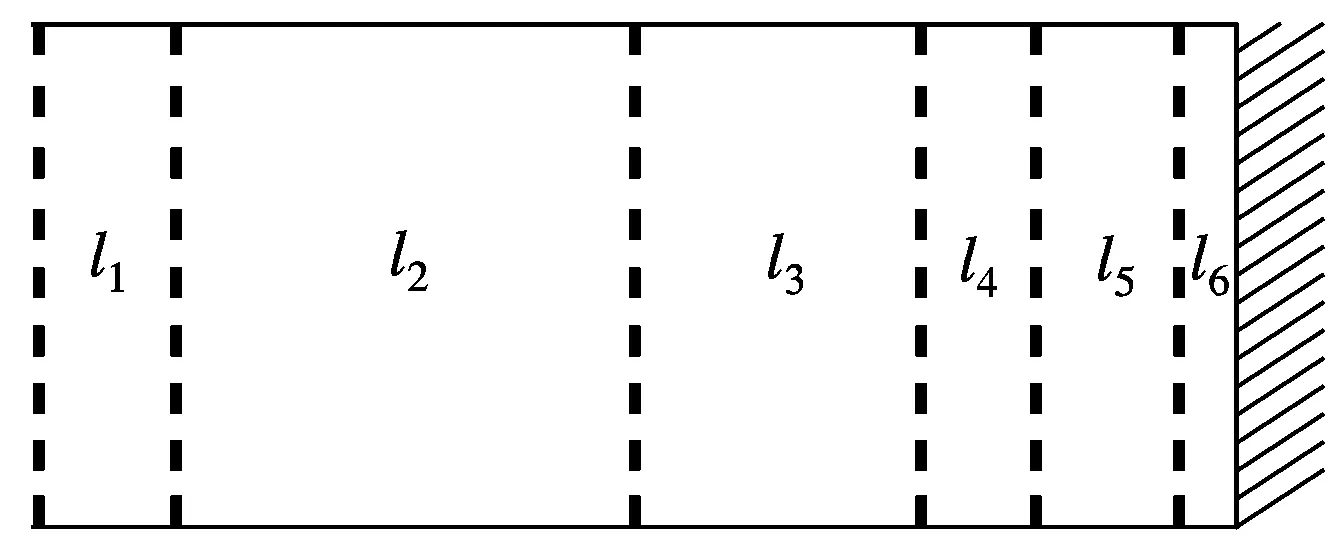
(b) 背腔串联MPP吸声体结构
实例1和2的数值结果显示,本文所提出的QRD-backed MPP吸声体正入射吸声系数解析计算方法准确、可靠,QRD-backed MPP吸声体具有明显优于单层MPP吸声体的吸声带宽,其多个共振峰来源于各个子背腔的分别共振吸声.基于经典QRD背腔深度比例,适当错开2组对称结构的子空腔深度,该类吸声体的吸声频带和吸声性能可得到进一步提升,吸声体实例2在460~3 500 Hz的频率范围内,正入射吸声系数不小于0.5,最大吸声系数达到0.98.
3 实验结果
为进一步验证所提出的QRD-backed MPP吸声体正入射吸声系数解析计算方法,本文基于实例2的设计参数制作了1∶1的吸声体实验样品,并在矩形驻波管中采用传递函数法[17]实验测量了其正入射吸声系数.图6为实验测量系统框图,其中,驻波管参数符合测量标准[17],壁体为15 mm厚的亚克力板,通道内截面尺寸为100 mm×100 mm,截止频率为1 700 Hz,有效测量频率范围为50~1 600 Hz;使用2只G.R.A.S 40AP的1/2英寸(1.27 cm)预极化声压场麦克风,测量管内壁声压信号,测量中心点相距5 cm;HiVi-M3S的3.5英寸(8.89cm)扬声器由B&K 2716的功率放大器驱动,安装在驻波管顶端并与管内壁有效密封连接.实验中使用B&K PULSE 3560D系统发出扫频信号并进行实时信号采集与分析.实验测量实景照片如图7所示,其中左上角插图为制作好的吸声体实验样品,其表面MPP由铝合金板制作,加工参数为:t=0.4 mm,d=0.4 mm,σ=1.8%,几何尺寸为97 mm×97 mm;其背腔结构由1 mm厚铝合金板使用Loctite 4062强力胶粘贴制作,各子背腔的宽度均为15 mm,深度依次为l1=25 mm,l2=100 mm,l3=50 mm,l4=10 mm,l5=20 mm,l6=5 mm.
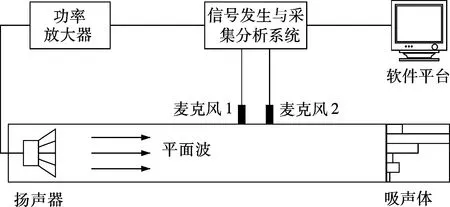
图6 吸声体正入射吸声系数实验测量系统框图
吸声体实验样品正入射吸声系数的解析计算、有限元数值计算的预测结果与实验测量结果见图8.虽然受本文设计的吸声体尺寸限制(每周期最小宽度100 mm),实验测量目前只能在100 mm×100 mm的驻波管中进行,有效测量范围受限在50~1 600 Hz,但该频段预测结果与实验结果吻合较好,这也证明了本文所提出的解析计算方法的准确性.然而图8中部分频率位置处, 预测结果与实验

图7 实验测量实景照片
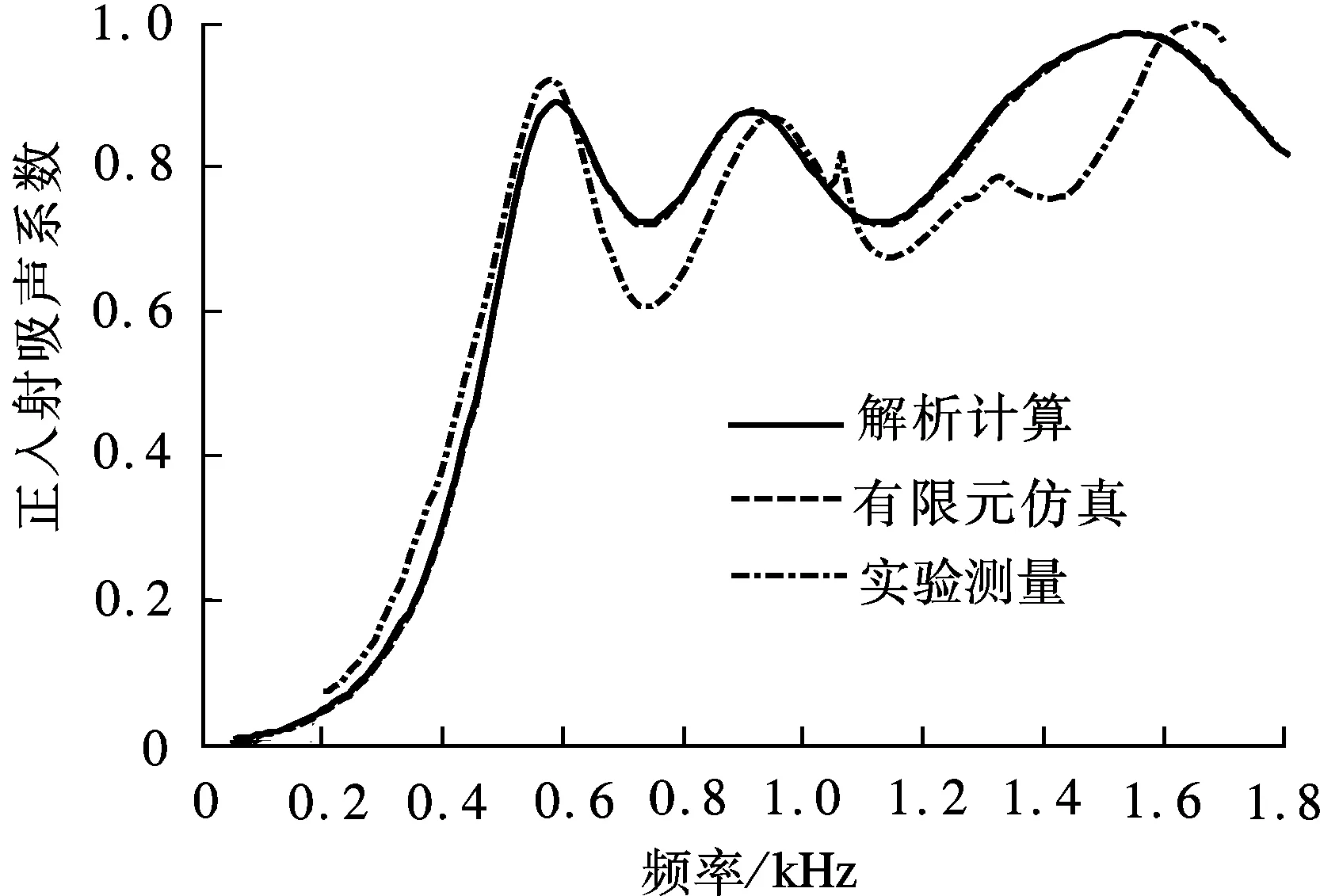
图8 实验测量与解析计算和有限元仿真的 吸声体正入射吸声系数结果对比
结果有明显偏差,如750 Hz左右的吸声谷处,两者有约17%的相对偏差;1 200~1 500 Hz的吸声峰位置处,实验结果共振峰位置向高频有所平移.实验过程中做了大量的验证性测量与调试来分析这些偏差来源,分析发现,上述偏差主要来源于吸声体实验样品的MPP加工误差:实验中设计的MPP穿孔直径较小(d=0.4 mm),存在一定的加工难度;虽采用了激光穿孔,但实际孔径仍与设计值存在约±10%的加工误差.导致MPP的实际声阻与声质量在一定程度上偏离了设计值,引起了实验误差.同时,吸声体的正入射表面尺寸为97 mm×97 mm,为便于推放于驻波管内,实验过程中吸声体四周与管内壁间约3 mm的缝隙使用不吸声的橡皮泥密封.而预测条件中假定的吸声体正入射吸声面积为100 mm×100 mm,这也是图8中预测结果与实验结果偏差的另一个可能来源.综上,目前实验结果已能证明本文所提出的QRD-backed MPP吸声体正入射吸声系数解析计算方法的准确性和有限元数值分析结果的可靠性,其中的实验误差有望在未来工作中进一步减少.
4 结语
本文详细探讨了一种由单层MPP和基于QRD深度序列设计的多个并联且深度不等的子背腔组成的新型MPP吸声体的吸声特性.首先提出了预测其正入射吸声系数的解析计算方法;然后采用有限元数值仿真和实验的方法对解析计算方法进行了验证,探讨了该类吸声体优化设计的基本方向.结果表明,本文提出的预测吸声体正入射吸声系数的解析计算方法是准确、可靠的,同时具有通用性.结果同时显示,相比单层MPP吸声体,该类新型吸声体的吸声频带显著加宽,且其多个共振吸声峰来源于各个子背腔的分别共振吸声.基于经典QRD背腔深度比例,适当错开2组对称结构的子空腔深度,该类吸声体的吸声频带和吸声性能可得到进一步提升:在460~3 500 Hz的频率范围内,吸声系数不小于0.5,最大吸声系数能达到0.98.本文讨论可为室内声学装修和噪声控制领域新型宽频带MPP吸声体的设计与开发提供参考.
References)
[1]马大猷. 微穿孔板吸声体结构的理论和设计[J]. 中国科学, 1975,18(1):38-50. Maa Dahyou. Theory and design of microperforated panel sound absorbing constructions [J].ScientiaSinica, 1975, 18(1):38-50. (in Chinese)
[2]马大猷. 微穿孔板结构的设计[J]. 声学学报,1988, 13(3):175-180. Maa Dahyou. Design of microperforated panel constructions[J].ActaAcustica, 1988, 13(3):175-180. (in Chinese)
[3]Park S H. Acoustic properties of micro-perforated panel absorbers backed by Helmholtz resonators for the improvement of low-frequency sound absorption[J].JournalofSoundandVibration, 2013, 332(20): 4895-4911. DOI:10.1016/j.jsv.2013.04.029.
[4]Zhao X D, Fan X Q. Enhancing low frequency sound absorption of micro-perforated panel absorbers by using mechanical impedance plates[J].AppliedAcoustics, 2015, 88:123-128. DOI:10.1016/j.apacoust.2014.08.015.
[5]Qian Y J, Kong D Y, Liu Y, et al. Improvement of sound absorption characteristics under low frequency for micro-perforated panel absorbers using super-aligned carbon nanotube arrays[J].AppliedAcoustics, 2014, 82:23-27. DOI:10.1016/j.apacoust.2014.02.014.
[6]盛胜我, 宋拥民, 王季卿. 微穿孔平板式空间吸声体的理论分析[J]. 声学学报, 2004, 29(4): 303-307. Sheng Shengwo, Song Yongmin, Wang Jiqing. Theoretical analysis of the acoustical characteristics of suspended micro-perforated panel[J].ActaAcustica, 2004, 29(4):303-307. (in Chinese)
[7]蔺磊, 王佐民, 姜在秀. 微穿孔共振吸声结构中吸声材料的作用[J]. 声学学报, 2010, 35(4): 385-392. Lin Lei, Wang Zuomin, Jiang Zaixu. Effect of sound-absorbing material on a microperforated absorbing construction[J].ActaAcustica, 2010,35(4):385-392. (in Chinese)
[8]Wang C Q, Huang L X. On the acoustic properties of parallel arrangement of multiple micro-perforated panel absorbers with different cavity depths[J].JournaloftheAcousticalSocietyofAmerica, 2011, 130(1): 208-218. DOI:10.1121/1.3596459.
[9]Fujiwara K, Miyajima T. Absorption characteristics of a practically constructed Schroeder diffuser of quadratic-residue type[J].AppliedAcoustics, 1992, 35(2): 149-152. DOI:10.1016/0003-682x(92)90029-r.
[10]Fujiwara K, Miyajima T. A study on the sound absorption of a quadratic-residue type diffuser[J].Acustica, 1995, 81(4): 370-378.
[11]Kuttruff H. Sound absorption by pseudostochastic diffusers (Schroeder diffusers)[J].AppliedAcoustics, 1994, 42(3): 215-231. DOI:10.1016/0003-682x(94)90110-4.
[12]Mechel F P. The wide-angle diffuser—A wide-angle absorber?[J].Acustica, 1995, 81(4):379-401.
[13]Wu T, Cox T J, Lam Y W. From a profiled diffuser to an optimized absorber[J].JournaloftheAcousticalSocietyofAmerica, 2000, 108(2): 643-650. DOI:10.1121/1.429596.
[14]Schroeder M R. Binaural dissimilarity and optimum ceilings for concert halls: More lateral sound diffusion[J].TheJournaloftheAcousticalSocietyofAmerica, 1979, 65(4): 958. DOI:10.1121/1.382601.
[15]Morse P M, Ingard K.Theoreticalacoustics[M]. New York: McGraw-Hill, 1968: 285-522.
[16]Maa D Y. Potential of microperforated panel absorber[J].TheJournaloftheAcousticalSocietyofAmerica, 1998, 104(5): 2861-2866. DOI:10.1121/1.423870.
[17]中华人民共和国国家质量监督检验检疫总局. GB/T 18696.2—2002声学 阻抗管中吸声系数和声阻抗的测量 第2部分:传递函数法[S]. 北京:中国标准出版社, 2002.
Absorption characteristics of micro-perforated panel sound absorbers with array of parallel-arranged sub-cavities with different depths
Min Hequn Guo Wencheng
(School of Architecture, Southeast University, Nanjing 210096, China) (Key Laboratory of Urban and Architectural Heritage Conservation of Ministry of Education, Southeast University, Nanjing 210096, China)
A new prototype of micro-perforated panel (MPP) sound absorber with supposed high sound absorption property in a wide frequency band is discussed. This kind of sound absorber included a single layered MPP and several cavities with different depths based on the depth sequence designed of the quadratic residue diffuser (QRD). First, an analytical method for evaluating the normal incidence absorption coefficients of this kind of absorber is presented. Secondly, the analytical method is validated by the simulations with the finite element method and the normal incidence absorption characteristics of the absorber are investigated as well. Finally, the corresponding experimental study is carried out, in which the normal incidence absorption coefficient of a prototype absorber is measured in a rectangular standing wave tube by the transfer function method. The experimental results show that the proposed analytical method is accurate and reliable. Besides, the normal incidence sound absorption coefficient of this kind of MPP absorber predicted by the analytical method is not smaller than 0.5 over the frequencies from 440 to 3 500 Hz, and the maximum sound absorption coefficients is 0.98.
micro-perforated panel; sound absorber; quadratic residue diffuser; finite element method; experiment
第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.030
2016-07-06. 作者简介: 闵鹤群(1981—),男,博士,副教授, hqmin@seu.edu.cn.
国家自然科学基金资助项目(51408113)、江苏省科技计划青年基金资助项目(BK20140623).
闵鹤群,郭文成.具有并联不等深度子背腔序列的微穿孔板吸声体吸声特性[J].东南大学学报(自然科学版),2017,47(1):177-183.
10.3969/j.issn.1001-0505.2017.01.030.
TU112;TU55
A
1001-0505(2017)01-0177-07
