故宫太和殿二层斗拱水平抗震性能试验
2017-02-21周乾杨娜淳庆
周 乾 杨 娜 淳 庆
(1北京交通大学土木建筑工程学院, 北京100044)(2故宫博物院, 北京100009)(3东南大学城市与建筑遗产保护教育部重点实验室, 南京 211189)
故宫太和殿二层斗拱水平抗震性能试验
周 乾1,2杨 娜1淳 庆3
(1北京交通大学土木建筑工程学院, 北京100044)(2故宫博物院, 北京100009)(3东南大学城市与建筑遗产保护教育部重点实验室, 南京 211189)
为更好地保护木构古建筑,对故宫太和殿二层斗拱开展了水平低周反复加载试验.制作了斗拱的1 ∶2缩尺比例模型,分别对其进行横向及纵向加载,研究其抗震参数.结果表明:相对于纵向加载,斗拱沿横向加载时更容易产生构件破坏.各斗拱极限承载力由大到小的顺序为:柱头科横向加载、平身科横向加载、角科加载、平身科纵向加载、柱头科纵向加载;延性系数由大到小的顺序为:柱头科纵向加载、平身科纵向加载、柱头科横向加载、角科加载、平身科横向加载;耗能能力由大到小的顺序为:角科加载、柱头科横向加载、平身科纵向加载、柱头科纵向加载、平身科横向加载;刚度退化程度由重至轻的顺序为:平身科横向加载、柱头科横向加载、角科加载、平身科纵向加载、柱头科纵向加载.太和殿二层斗拱的水平刚度模型可简化为三折线段形式.
太和殿;二层斗拱;地震;古建筑
斗拱是我国木构古建的重要力学构造之一,它是一种由拱、翘、升等小构件叠加起来的组合结构[1].近年来,国内外部分学者对斗拱的力学性能开展了研究.周乾等[2-3]基于调查分析,对故宫古建筑中斗拱的典型抗震构造问题进行了研究,认为斗拱典型问题包括松动、变形、开裂等,采取重新安装、局部更换、胶粘、化学加固、铁件加固等方法均可实现斗拱的有效加固;此外,他们采取静力加载试验方法,以故宫太和殿一层斗拱为研究对象,探讨了明清斗拱的轴压受力性能,认为太和殿一层斗拱的坐斗及与之相交的头翘、正心瓜拱容易破坏,下层构件受力小于上层构件,且溜金斗拱后尾受到的内力不大.袁建力等[4]以辽代应县木塔斗拱为研究对象,依据试验模型的力学参数,通过对斗拱结构构造进行简化,提出了基于摩擦-剪切耗能的有限元模型.邵云等[5]采取低周反复加载试验方法,分别对宋(6攒,含补间、柱头、转角形式,4~6铺作)、清(3踩柱头科)斗拱进行了初步研究,认为宋式斗拱在抗侧刚度及承载力方面均大于清式斗拱.阙泽利等[6]采用振动台试验方法,研究了明代甪直天王殿松木斗拱的动力特性,认为地震波频率对斗拱的变形起重要作用,斗拱整体变形与构件变形密切相关,且在地震作用下斗拱整体性能较好.谢启芳等[7]以辽代独乐寺观音阁平座层叉柱造式斗拱为研究对象,参照宋《营造法式》三等材的营造方法,制作了5个叉柱造式斗拱节点,通过低周反复荷载试验,研究了上述斗拱的抗震性能,认为各斗拱的弯矩-转角滞回曲线呈S形,滞回环有明显的捏缩效应.Yeo等[8]采取振动台试验方法,研究了中国台湾地区含斗拱木构架的抗震性能,认为地震作用下,斗拱部位首先是下部坐斗破坏,随后是与之相邻的拱、枋构件产生破坏.文献[9-10]采用低周反复加载试验方法,研究了日本寺庙建筑中类似于五踩斗拱的抗震性能,认为斗拱的恢复力模型应采用三折线段表示;斗拱在地震作用下产生变形的主要影响因素为坐斗变形;在进行数值分析时,斗拱总刚度可由若干串、并联弹簧来模拟.Lee等[11]通过对考虑斗拱连接的韩国古建筑试验模型进行整体推拉试验,获得了斗拱的双线性刚度参数恢复力模型,并认为在结构有限元模拟中,可用剪切弹簧单元来模拟斗拱力学机制.基于已有成果,本文以故宫太和殿二层斗拱为例,采取水平低周反复加载试验方法,开展明清官式木构古建筑斗拱水平抗震性能研究,讨论了不同加载条件下不同类型斗拱的抗震性能,提出了各斗拱水平刚度的简化计算模型,结果可为我国古建筑保护和维修提供理论参考.
1 试验
1.1 构造简介
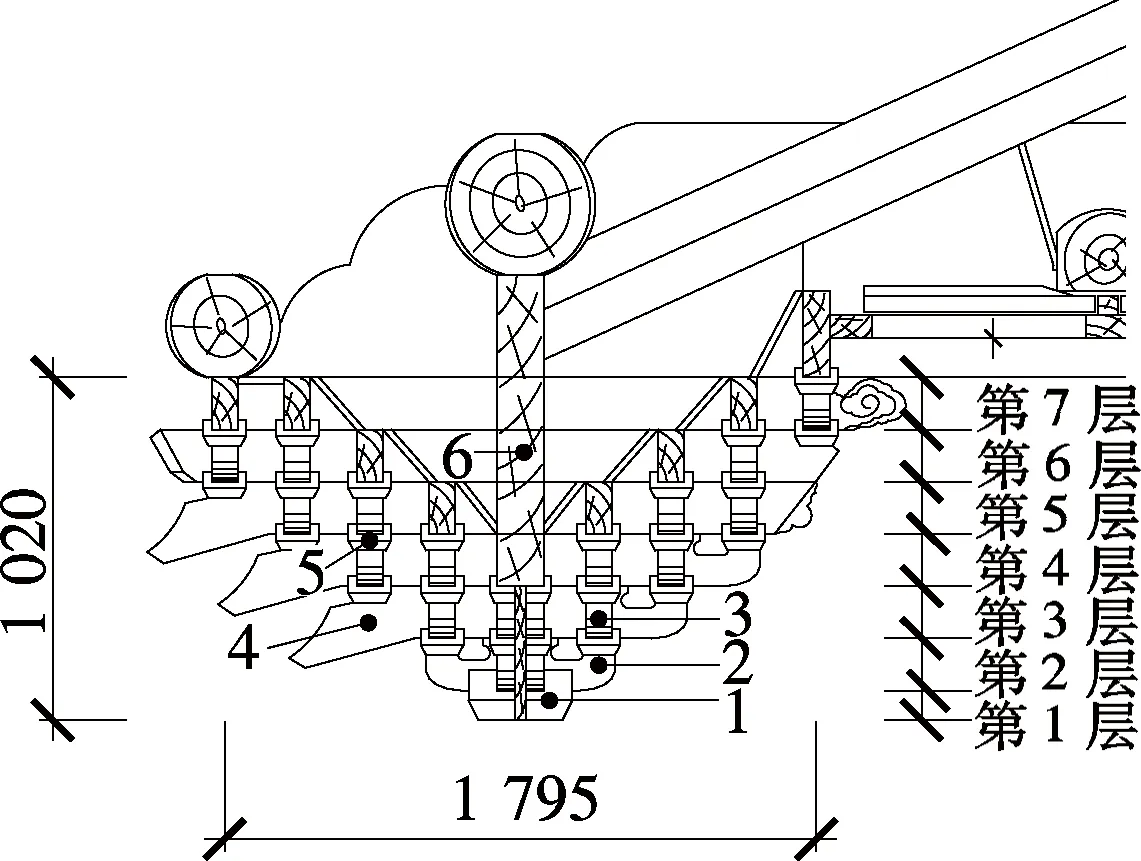
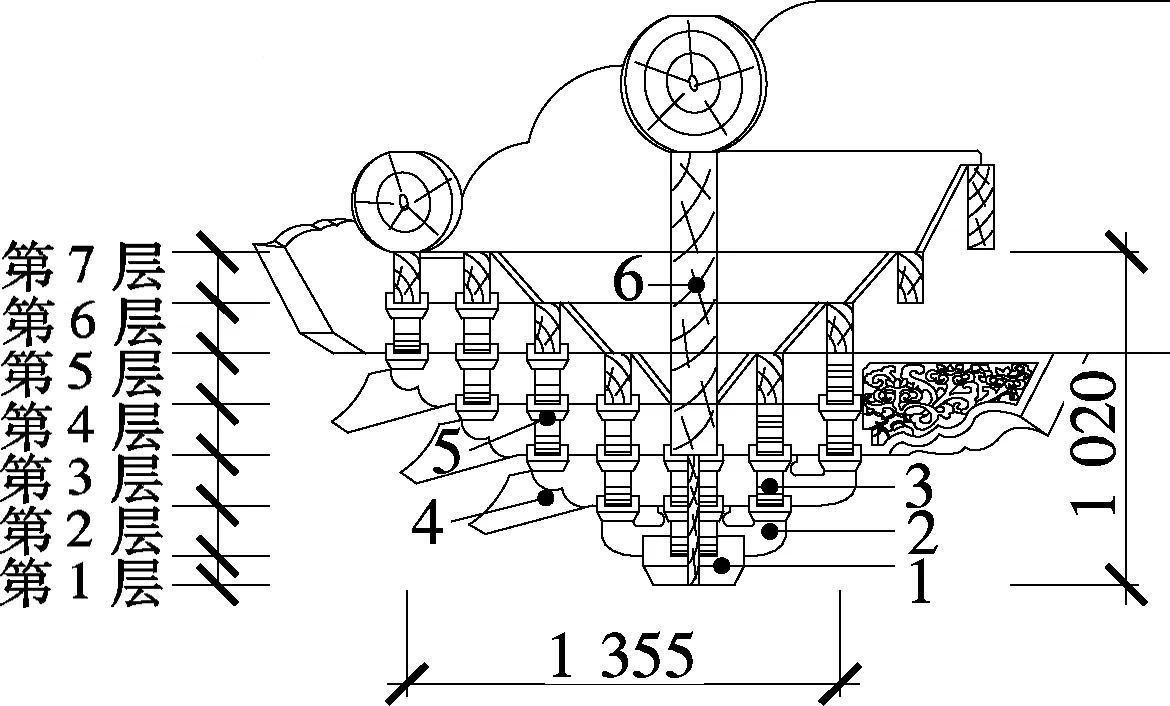
斗拱向外出挑,可称为出踩;向外出挑一拽架称为三踩,出挑二拽架称为五踩,依此类推,斗拱出踩数目越多,斗拱所在的建筑等级越高[12].作为明清最高级别宫殿建筑,太和殿二层檐斗拱属单翘三昂九踩斗拱做法,斗拱高度(坐斗底皮至挑檐桁下皮的垂直距离) 约1 020 mm,外檐出挑尺寸(坐斗中心至挑檐枋中心的水平距离)约900 mm.上檐斗拱的主要类型包括平身科、柱头科和角科斗拱3种.其中,平身科斗拱共146攒,柱头科斗拱共16攒,角科斗拱共4攒.从构造上讲,上述各斗拱均包括斗(坐斗、十八斗)、拱(正心瓜拱、正心万拱、单才瓜拱、单才万拱、厢拱等)、翘、升(槽升子、三才升)、昂(头昂、二昂等)、枋(正心枋、拽枋)等构件[13].太和殿上檐各类型斗拱分层构造见图1.
(a) 平身科
(b) 柱头科

(c) 角科
1—坐斗;2—翘;3—单才瓜拱;4—头昂;5—三才升;6—正心枋
图1 太和殿二层斗拱纵剖图(单位:mm)
1.2 模型制作
采用故宫大修用的红松材料,制作太和殿二层斗拱1∶2比例模型3个,含平身科、柱头科、角科斗拱各1个.木材密度为460 kg/m3,含水率约为13.2%,顺纹抗拉强度为98.1 MPa,顺纹抗压强度为34.6 MPa,顺纹弹性模量为9 316 MPa,横纹局部抗压强度为21.1 MPa.各斗拱模型的主要构件尺寸见表1.
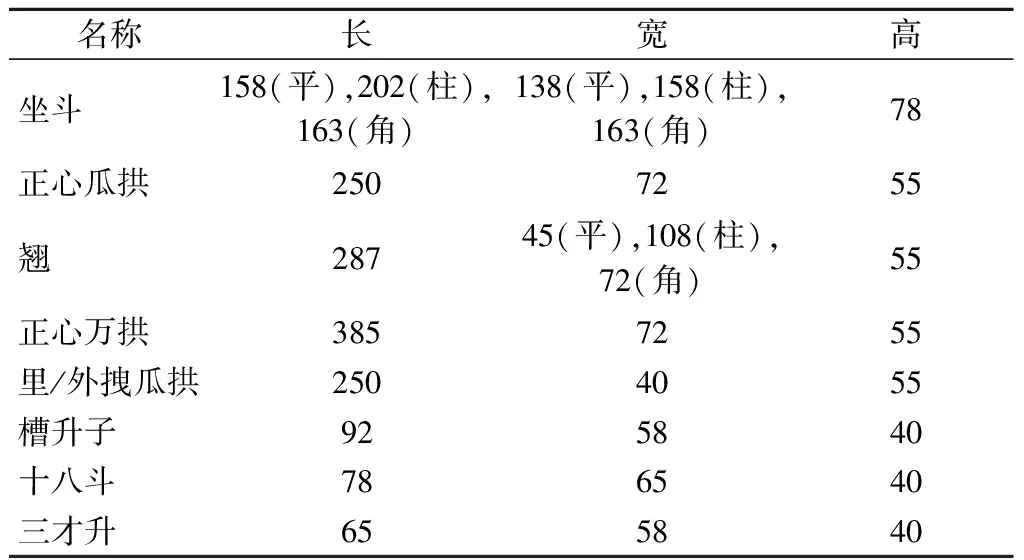
表1 斗拱模型主要构件尺寸 mm
注:平表示平身科;柱表示柱头科;角表示角科.
1.3 加载方案
采用水平低周反复加载试验来研究各斗拱的水平抗震性能.对于平身科、柱头科斗拱而言,由于斗拱在纵向及横向的受力状态并不相同,因而分别采取纵向加载及横向加载方式(见图2(a)和(b)).纵向加载即荷载作用方向与拱、枋方向平行;横向加载即荷载作用方向与拱、枋方向垂直.首先对上述斗拱进行纵向加载试验,结束后替换产生变形、开裂的斗拱构件,再进行横向加载试验.对于角科斗拱而言,由于其在平面布局上为沿45°斜线的对称结构,因而加载方向为斗拱正交方向之一(见图2(c)).
(a) 平身科
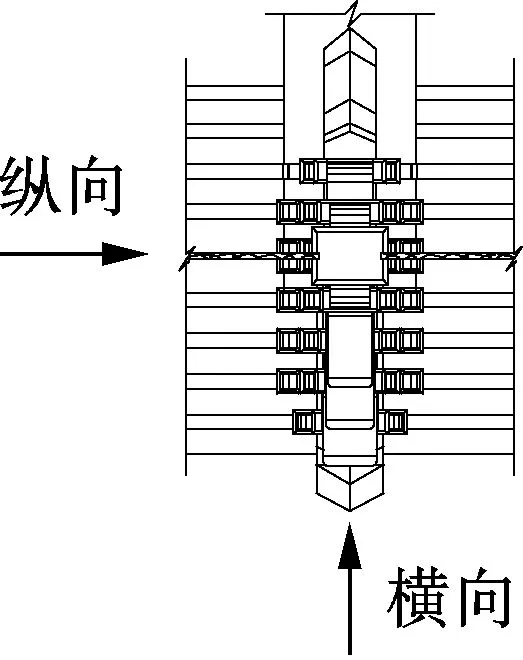
(b) 柱头科
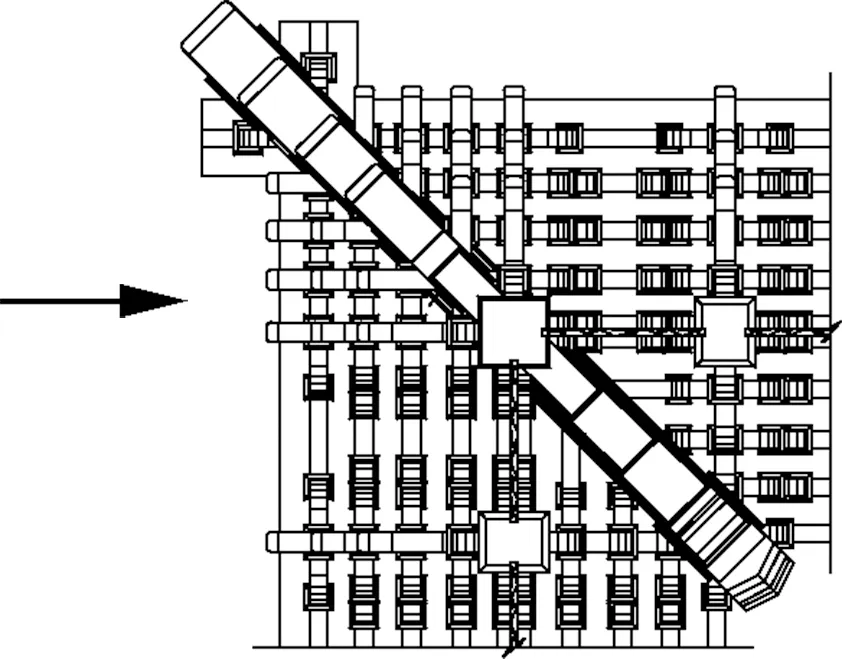
(c) 角科
为便于加载,各斗拱模型均倒立放置,且底部固定在基座上.加载时,首先通过竖向千斤顶在坐斗顶部施加恒定的竖向荷载,以模拟太和殿二层斗拱上部的实际荷载.该竖向千斤顶位于门式加载架的顶部反力梁上,并通过设置水平向滚轴支座来保持竖向荷载在试验过程中固定不变.考虑模型相似性关系,取二层各斗拱坐斗上部平身科、柱头科、角科的竖向恒载值分别为8.25, 11.75, 12.50 kN.然后,通过水平千斤顶施加低周反复荷载.水平千斤顶加载时,一端通过与之相连的套筒来推拉斗拱,另一端则固定在反力墙上.
试验中主要测定的参数为斗拱受到的水平力F和水平位移u.将2个力传感器分别与水平及竖向千斤顶相连,以测定力的大小.第1个力传感器用于测定F,第2个力传感器用于加载时控制竖向荷载.分别在各斗拱顶板、由上往下第3层、由上往下第5层位置处设置位移计,以测定斗拱典型位置的水平侧移,则u为各层相对水平侧移之和.采取位移控制加载方式进行试验,初始位移约为3 mm,后面每级增量约为3 mm,每级位移循环1次,加载速度控制为0.15 mm/s.当水平力传感器读数下降至峰值的85%左右或斗拱产生威胁到整体安全的侧移或破坏症状时,试验结束.各斗拱的水平位移u控制在33~39 mm范围内.以二层平身科斗拱横向加载为例,模型加载装置示意图见图3.
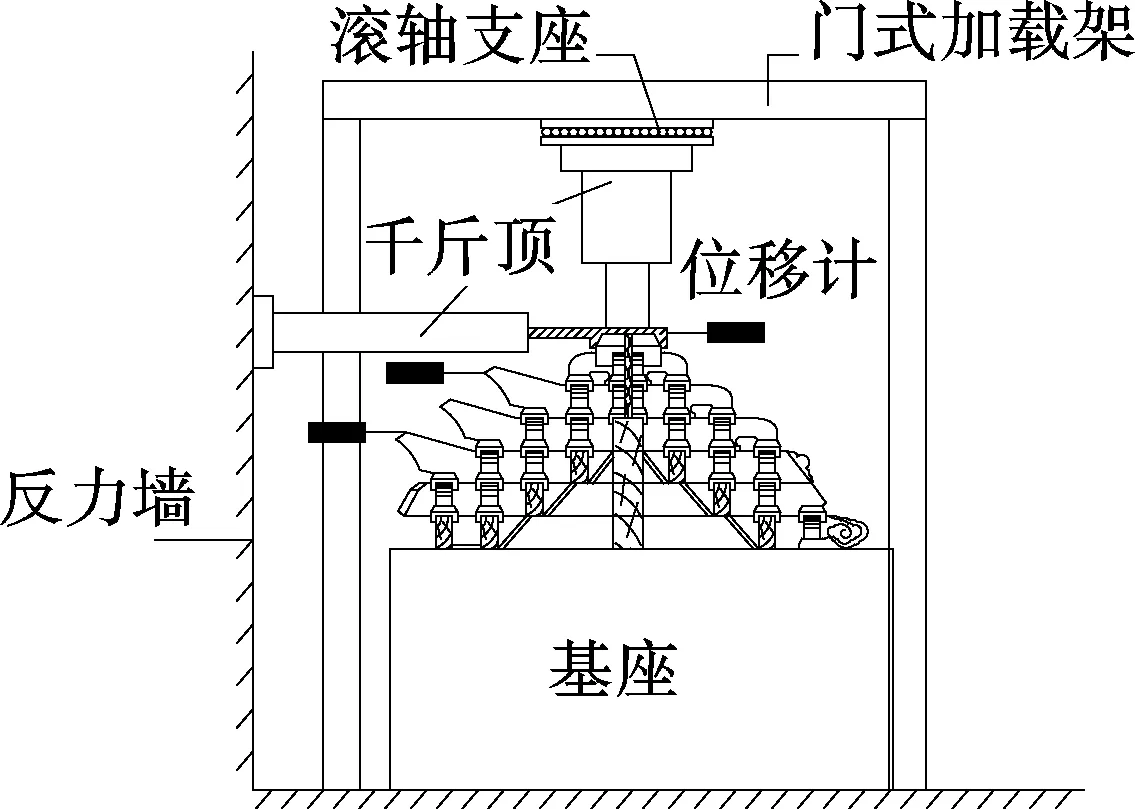
图3 太和殿二层平身科斗拱横向加载装置示意图
2 试验现象
由于斗拱是倒放加载的,为便于开展论述,本文统一称坐斗处于最上层,其余构件按构造往下分层.此外,本文统一设定推向加载为正向加载,拉向加载为反向加载.试验现象中相同点主要表现为:① 吱声.加载时,各斗拱构件之间挤压和咬合过程中会发出吱声.u较小时,上部传来轻微吱声,且主要发生在坐斗及其附近构件上;u较大时,加载过程中吱声紧密,偶尔伴有劈裂声,说明部分小截面尺寸构件因挤压、剪切产生开裂过程.② 变形.水平荷载作用下,各斗拱均会产生变形甚至出现构件破坏情况.斗拱变形特点均表现为上部坐斗及周边构件变形明显,而下部正心枋、拽枋等构件的变形则相对较小.
下面分别阐述试验现象中的不同点.在平身科纵向加载试验中,随着水平位移u的增加,斗拱变形表现为斗拱整体以底部边线为轴,近似发生整体倾斜(转动).尽管斗拱由很多小构件组装而成,且木构件因挤压变形易产生相对摩擦滑移现象,但从试验现象来看,纵向加载时,斗拱构件间的相互挤压和咬合作用较相对滑移明显,斗拱整体性能较好.从斗拱整体来看,试验后未发现有明显劈裂或翘曲的构件(不排除有个别构件因挤压、剪切产生轻微局部破坏),斗拱整体保持较完好.二层平身科斗拱纵向加载试验照片见图4.图中椭圆圈部分为斗拱整体倾斜时与底部局部分离时产生的空隙.

图4 二层平身科斗拱纵向加载试验照片
在柱头科纵向加载试验中,当水平位移u增大时,坐斗带动下部构件产生倾斜.加载过程中,槽升子、三才升等小构件并未产生破坏.十八斗双向与昂、拱咬合,在试验过程中产生倾斜.当u进一步增大时,斗拱产生整体倾斜幅度增大,但因为构件少、侧移尺寸大,斗拱构件间的空隙较大,摩擦滑移作用大于彼此间的挤压咬合作用,斗拱未出现明显破坏,说明斗拱在该加载方向上具有较好的整体性能.太和殿二层柱头科斗拱纵向加载试验照片见图5.

图5 二层柱头科斗拱纵向加载试验照片
太和殿二层角科斗拱加载试验照片见图6.当u=12 mm时,正心瓜拱与头翘相交的十八斗⑥相交位置开始产生分离,预示着斗拱整体性开始变差;u=21 mm时,十八斗⑥出现裂纹,但尚能使用;u=24 mm时,斗拱下部三才升⑦因挤压变形产生错位;u=27 mm时,斗拱恢复到平衡位置,部分构件的变形不能完全恢复,表现为正心枋③、拽枋④轻微错位,与头昂相交的槽升子⑤掉落,十八斗⑥脱离连接并完全破坏;u=30 mm时,头昂后尾①偏离二昂后尾②顶面约30 mm;u=39 mm时,头昂尾部①受附近构件挤压,其运动几乎脱离与之相交的二昂后尾②顶部,可近似认为斗拱失效.

在平身科横向加载试验中,随着u的增大,斗拱变形特点表现为上部坐斗及正心瓜拱、头翘等构件产生平移,下部正心枋、外拽枋、三才升等构件则产生不明显的倾斜.u达到各级控制位移附近时斗拱表现出来的变形比较明显,而在平衡位置附近,斗拱变形恢复较为迅速,说明斗拱整体具有较好的变形能力.当u=36 mm时,斗拱出现破坏,形式为坐斗的严重偏移.该偏移导致竖向加载装置从坐斗顶面上滑移并失效.相关试验照片见图7.

图7 二层平身科斗拱横向加载试验照片
在柱头科横向加载试验中,当u=18 mm时,正心万拱与正心枋存在可见错动,说明斗拱整体变形不一致;当u=21 mm时,头昂与单才瓜拱搭接处的三才升分别产生挤压破坏;当u=30 mm时,头昂端部与十八斗产生分离;当u=33 mm时,斗拱上部构件错动明显(由于构件间空隙增大及部分构件局部破坏,摩擦构件间摩擦滑移作用增强),其整体性变差,桃尖梁则产生较为明显的倾斜.相关试验照片见图8.

3 结果与分析
3.1 F-u滞回曲线
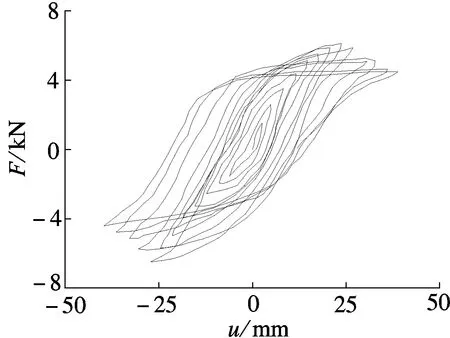
各斗拱的F-u滞回曲线见图9.
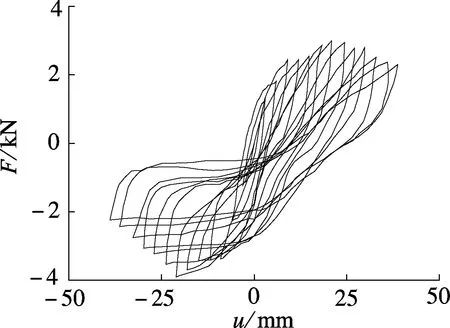
由图9(a)可知,平身科纵向加载所得的F-u滞回曲线形状以反S形为主,说明斗拱在受荷过程中存在摩擦滑移.各曲线在加载初始阶段刚度较大,表明斗拱加载初始阶段时构件的相互挤紧状态较为明显;随着u的逐渐增大,曲线趋于平缓,说明斗拱在每级控制位移较大时具有较好的延性.在控制位移处卸载时,斗拱刚度下降较明显,说明其自身恢复力较差.滞回环包络面积较为饱满,反映出斗拱的耗能能力较好.
由图9(b)可知,柱头科纵向加载所得的F-u滞回曲线形状在受推阶段近似为弓形,在受拉阶段近似为Z形,说明受推过程中构件间挤压和剪切作用明显.曲线在受推阶段的斜率明显大于受拉阶段,说明斗拱在推拉过程中的变形能力不同,受拉阶段的延性更好.曲线下降段刚度降低比较明显,表明斗拱的自身恢复力较差.从滞回环饱满程度来看,斗拱在整个加载过程中的耗能性能略差.
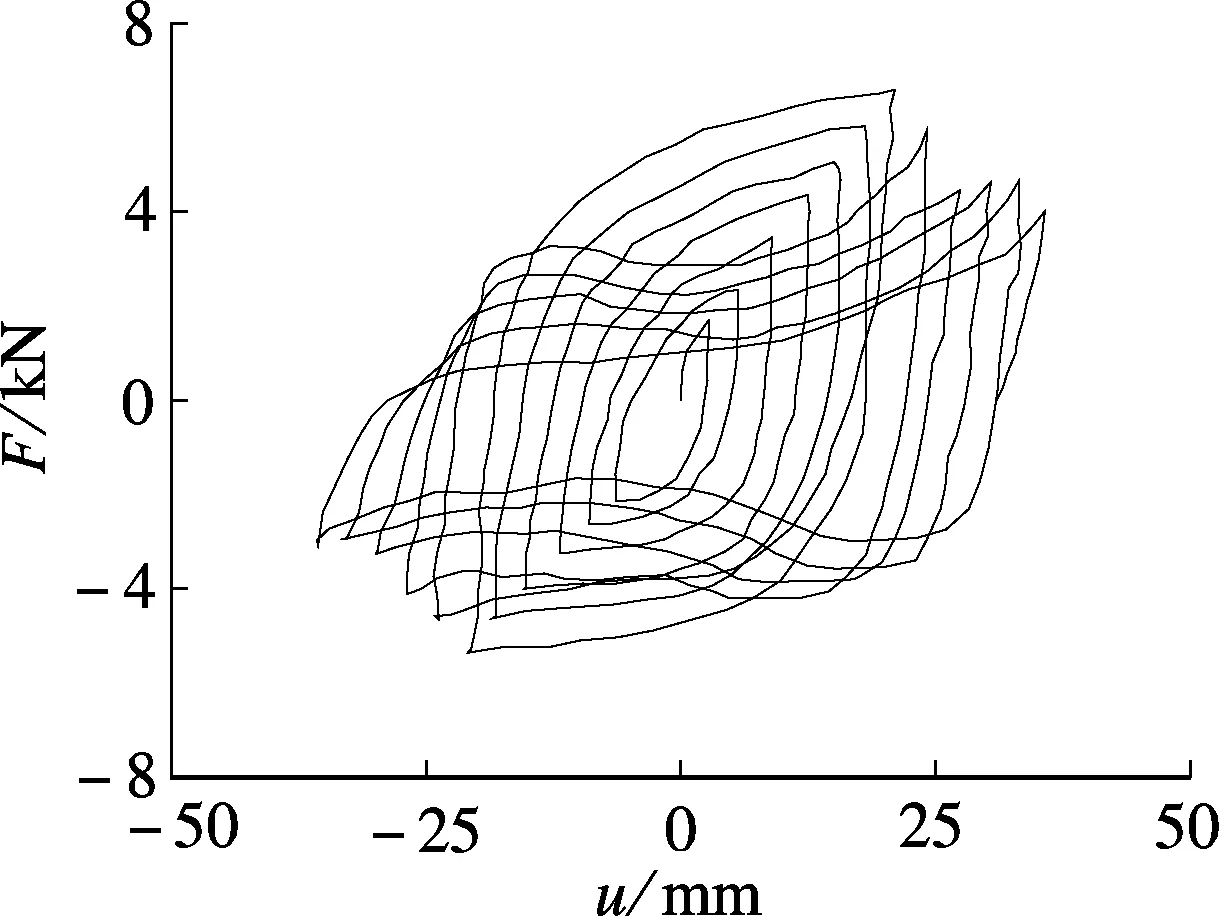
由图9(c)可知,角科加载所得的F-u滞回曲线形状较复杂,当u≤24 mm时,表现为斗拱构件挤压、剪切作用较为明显的梭形;当u>24 mm时,表现为构件摩擦滑移相互作用较为明显的Z形.曲线上升段刚度增长趋于平缓,说明斗拱具有较好的延性;下降段刚度下降迅速,表明斗拱恢复力较差.滞回环包络面积在u较小时比较饱满,u较大时则相对变小,说明随着u值的增大,斗拱的耗能能力逐渐减弱.
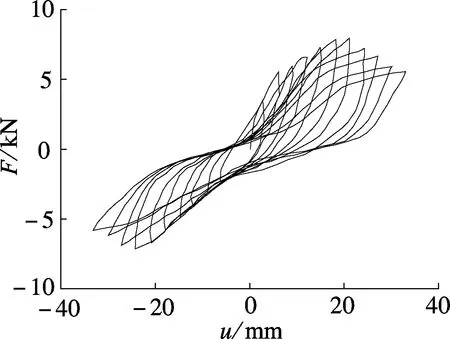
由图9(d)可知,平身科横向加载所得的F-u滞回曲线形状为弓形,中部具有一定的捏缩性,说明斗拱构件在受力过程中既存在摩擦滑移,又存在剪切作用.曲线上升段斜率增加不明显,表明斗拱具有较好的延性.滞回环包络面积不饱满,说明斗拱的耗能性能略差.
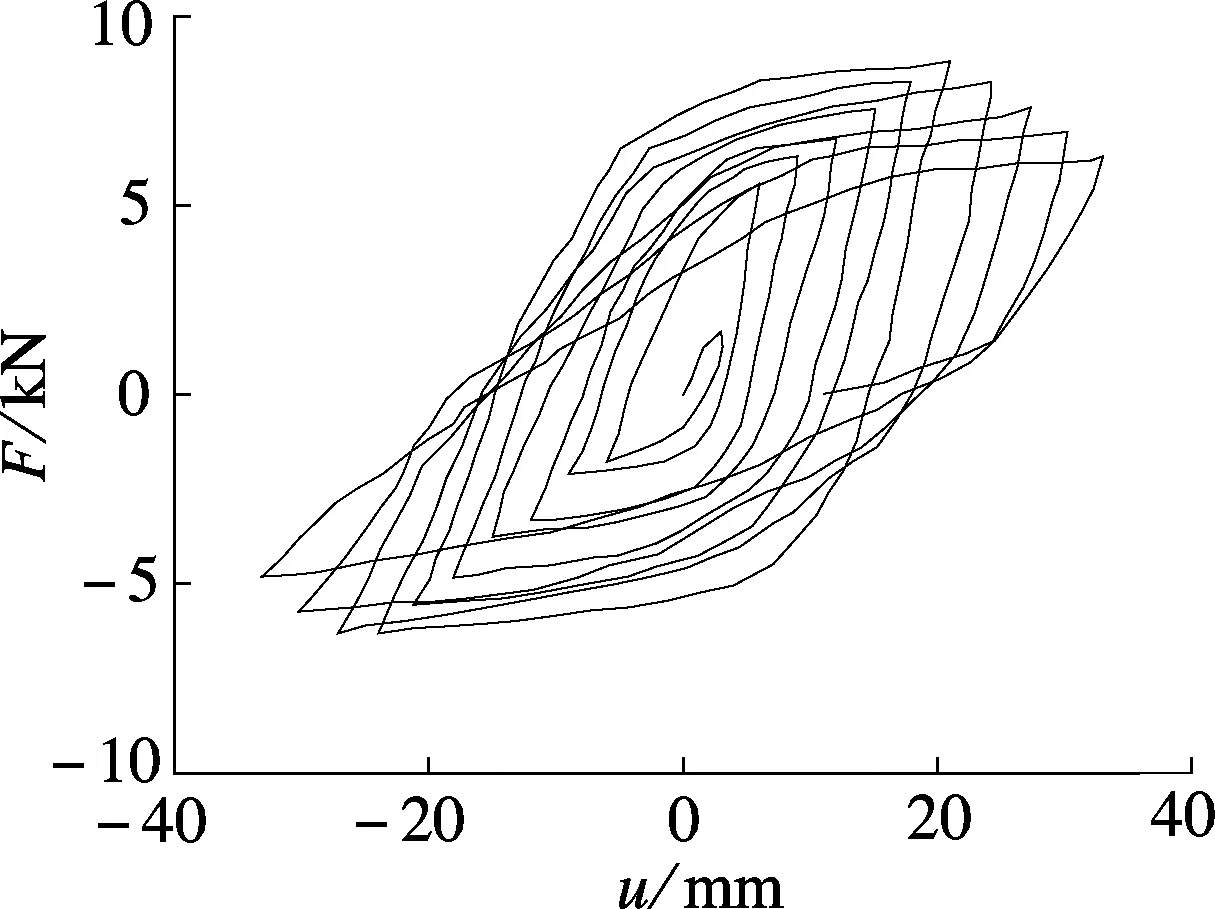
由图9(e)可知, 柱头科横向加载所得F-u滞回曲线形状为梭形,说明斗拱受到的侧向压力较明显.曲线上升阶段刚度增长逐渐平缓,表明斗拱具有较好的延性;卸载时斗拱刚度下降明显,说明斗拱恢复力较差.当u较小时,滞回环较饱满,说明该加载条件下斗拱的耗能性能较好;随着u的增加,滞回环饱满程度降低,斗拱耗能性能减弱.
3.2 F-u骨架曲线
将图9中各斗拱F-u滞回曲线的峰值点相连,可获得F-u骨架曲线,结果见图10.由图可知,各骨架曲线均存在较明显的上升段和下降段,分别对应于水平荷载作用下的屈服及破坏过程,且各曲线总体较为平缓,说明大部分斗拱具有较好的延性.各骨架曲线的不同点表现为:① 极限承载力不同.各斗拱在推向、拉向加载极限荷载值Fm见表2.由表可知,各斗拱的极限承载力由大至小的顺序为:柱头科横向加载、平身科横向加载、角科加载、平身科纵向加载、柱头科纵向加载.这与斗拱构造特征及加载方向密切相关.从加载方向来看,横向加载条件下斗拱构件间的挤压咬合作用明显,所需外力较大;纵向加载条件下,斗拱构件间的摩擦滑移作用表现明显,所需外力较小.从斗拱构造来看,平身科、柱头科、角科的斗拱高度相同,但柱头科斗拱构件数量最少,其桃尖梁截面尺寸远大于其他构件,横向加载条件下不易产生变形,因而极限承载力最大;纵向加载条件下,其参与摩擦滑移作用的构件最少,因而极限承载力最小.同理,平身科斗拱数量多于柱头科,横向加载条件下的极限承载力小于柱头科,而纵向加载条件下的极限承载力大于柱头科.② 曲线刚度发展变化程度不同.在上升阶段,横向加载斗拱的刚度明显大于纵向加载;在下降阶段,横向加载斗拱的刚度退化明显大于纵向加载.
(a) 平身科纵向加载
(b) 柱头科纵向加载
(c) 角科加载
(d) 平身科横向加载
(e) 柱头科横向加载
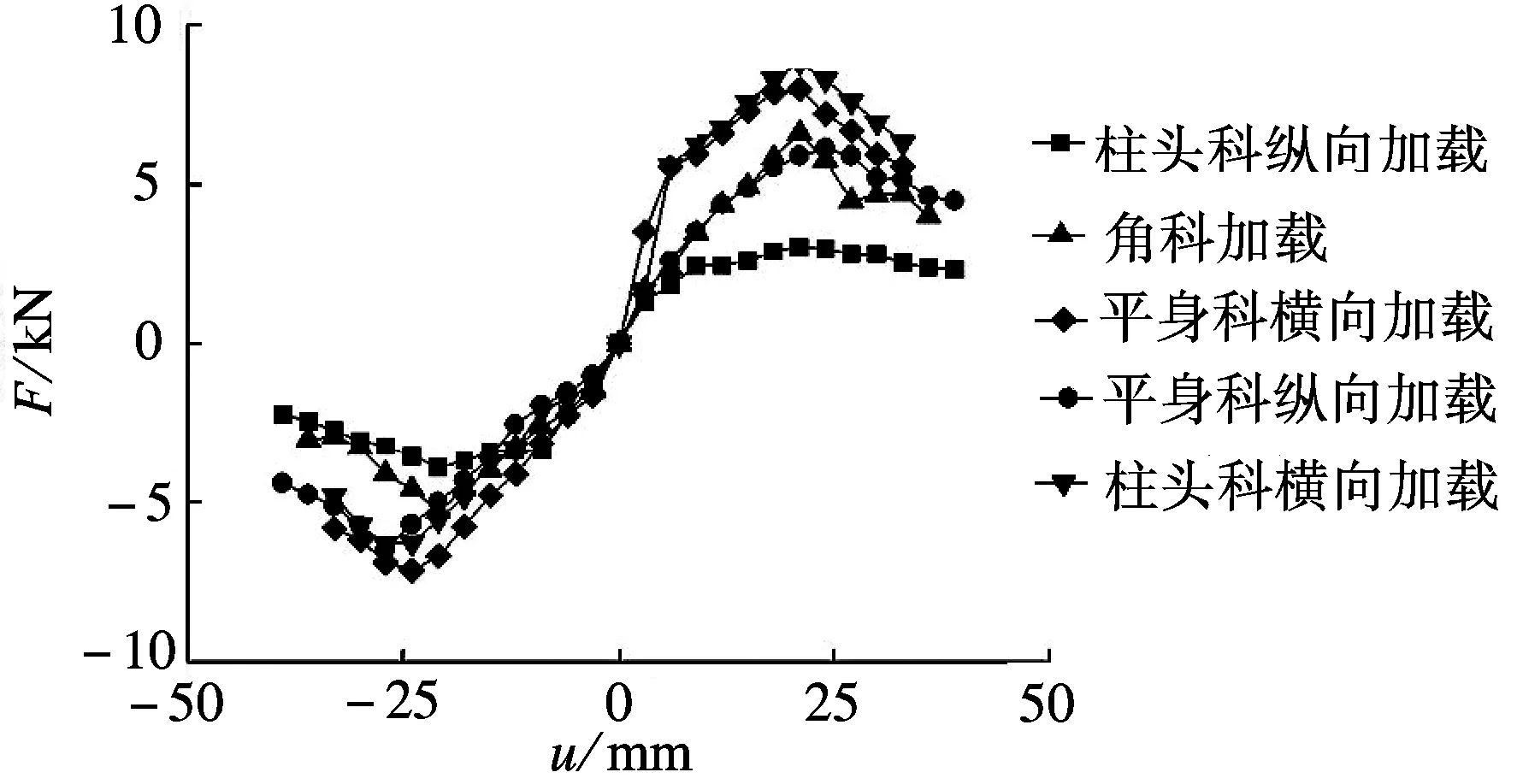
图10 太和殿二层斗拱F-u骨架曲线
3.3 延性性能
太和殿二层斗拱的延性性能采用位移延性系数表示,其计算公式为[14]
(1)
式中,um,uy分别为斗拱的极限位移和屈服位移.由于木材为非线性材料,无明显屈服点,因而采取文献[15]推荐的骨架曲线所包面积互等方法求解uy.
对试验中获得的各数据进行计算分析,得到太和殿二层斗拱的特征参数,结果见表2.由表可知,对于不同类型斗拱而言,无论是纵向加载还是横向加载,柱头科斗拱的μ值大于平身科.结合斗拱构造及试验现象分析可知,柱头科斗拱构件数量比平身科少,且包含截面尺寸明显大于其他构件的桃尖梁头,斗拱整体性更好.水平荷载作用下,无论对斗拱进行横向加载还是纵向加载,柱头科斗拱的整体变形能力优于平身科斗拱.各斗拱横向加载时的μ值明显小于纵向加载时的情况,说明斗拱在纵向受力时具有更好的延性.对于各斗拱而言,推向和拉向加载的μ值并不相同,说明推向和拉向的延性各不相同.不同斗拱的μ值由大到小顺序排列为:柱头科纵向加载、平身科纵向加载、柱头科横向加载、角科加载、平身科横向加载.
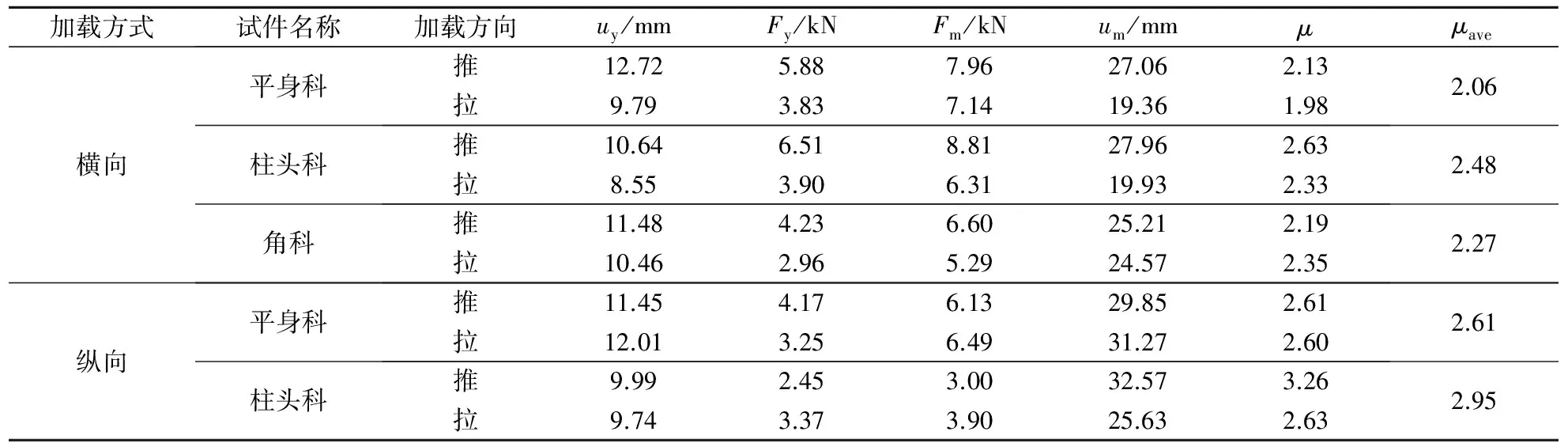
表2 太和殿二层斗拱特征参数
注:Fm,Fy分别为斗拱的极限荷载和屈服荷载;μave为μ的均值;角科斗拱由于构造原因,其纵向加载与横向加载方式相同.
3.4 耗能能力
采用等效黏滞阻尼系数he来评价太和殿二层斗拱的耗能性能,he越大,斗拱的耗能性能越好[15].
图11给出了各斗拱的he-u曲线.由图可知,随着u的增大,各斗拱的等效黏滞阻尼系数均表现为先增大后减小的趋势.这说明在加载初期,u较小时,斗拱各构件处于初步挤紧阶段,其耗能能力尚未发挥;随着u的增大,斗拱间作用增强,纵向加载斗拱表现出较大的摩擦滑移,横向加载斗拱表现出较明显的挤压和咬合,2种加载方式均使斗拱耗能能力增强;当u值进一步增加时,由于外力增大,斗拱构件产生变形、破坏、较大空隙等问题,导致耗能能力相对降低.对于平身科斗拱而言,纵向加载条件下的he值大于横向加载条件下的he值;对于柱头科斗拱而言,横向加载条件下的he值则大于纵向加载条件下的he值;对于角科斗拱而言,其he值为所有斗拱中出现的最大值.各斗拱的耗能性能由大到小的顺序为:角科加载、柱头科横向加载、平身科纵向加载、柱头科纵向加载、平身科横向加载.
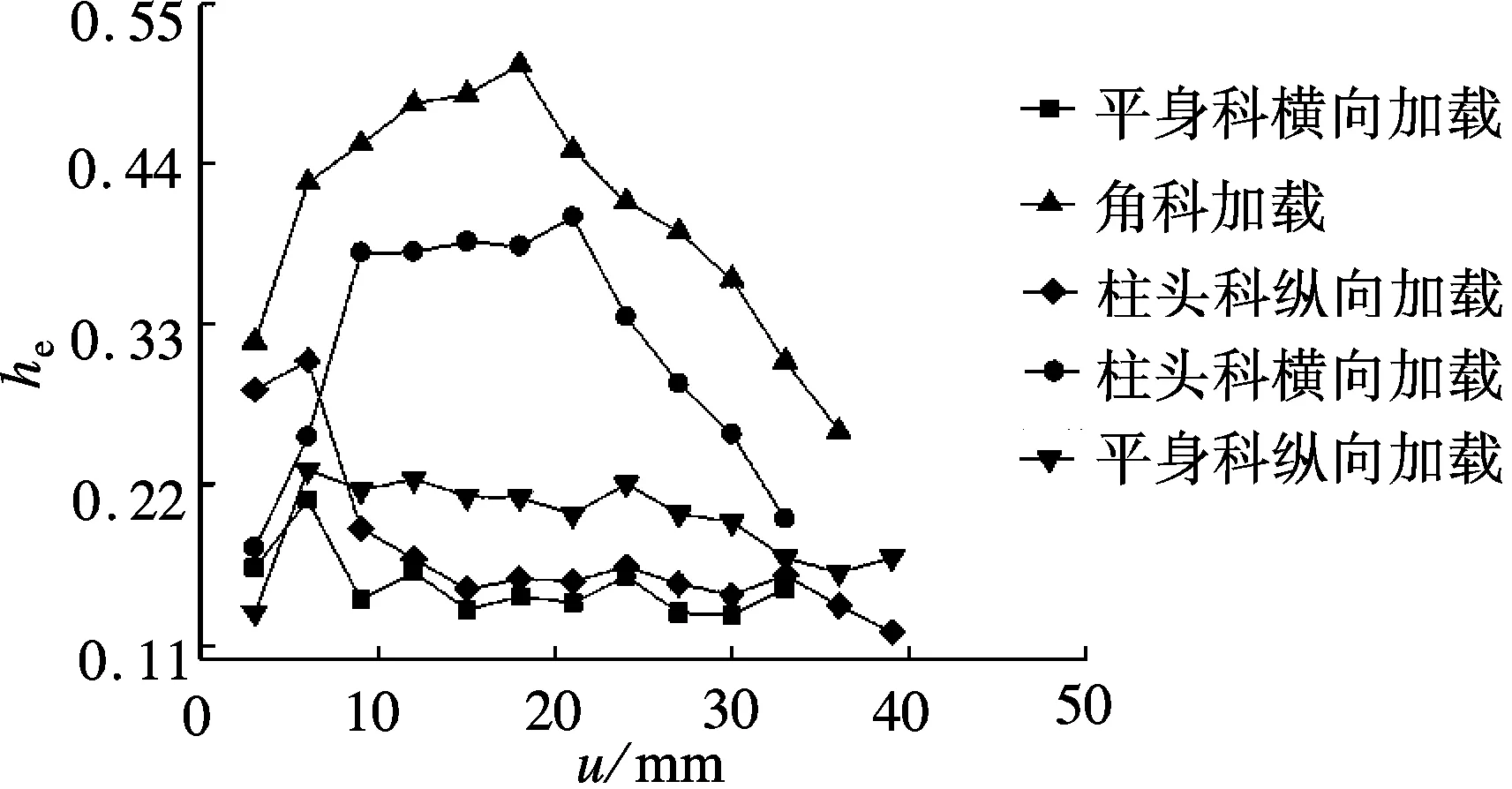
图11 太和殿二层斗拱he-u曲线
3.5 刚度退化
斗拱在每次达到控制位移时的水平刚度为
(2)
式中,ki为第i级荷载作用下斗拱的水平刚度;Fi为第i级荷载峰值;ui为第i级荷载峰值对应的斗拱水平位移.
基于试验数据,绘出各斗拱的k-u曲线,结果见图12.由图可知,推向和拉向加载时,斗拱的k值并不相同,且横向加载相对于纵向加载而言,其非对称性表现更为明显;究其原因在于,斗拱为非对称结构,推向和拉向加载时的受力机制并不完全相同.各斗拱的k值随着u值的增大而逐渐减小,即出现退化现象.不同斗拱的k值退化程度由重至轻的顺序为:平身科横向加载、柱头科横向加载、角科加载、平身科纵向加载、柱头科纵向加载.这是因为角科的分层截面尺寸较平身科、柱头科大,斗拱构件之间的摩擦滑移运动相对更明显,横向加载条件下,u较小时,平身科、柱头科斗拱各构件挤压程度较角科明显,所需F值更大;u值较大时,前两者以整体变形为主或构件间出现明显破坏,所需F值明显下降,因而在整个加载过程中较后者的刚度退化更明显.纵向加载条件下,u较小时,平身科、柱头科斗拱构件间的摩擦滑移较角科明显,k值较小;u较大时,后者由于部分构件破坏导致挤压作用减弱、摩擦滑移增强,F值下降更明显,因而k值的退化程度较前两者明显.另外,平身科斗拱的k值退化较柱头科斗拱更明显,其主要原因在于,平身科斗拱构件数量更多,构件之间存在大量间隙,荷载作用下,间隙扩展加快了k值退化的进程.
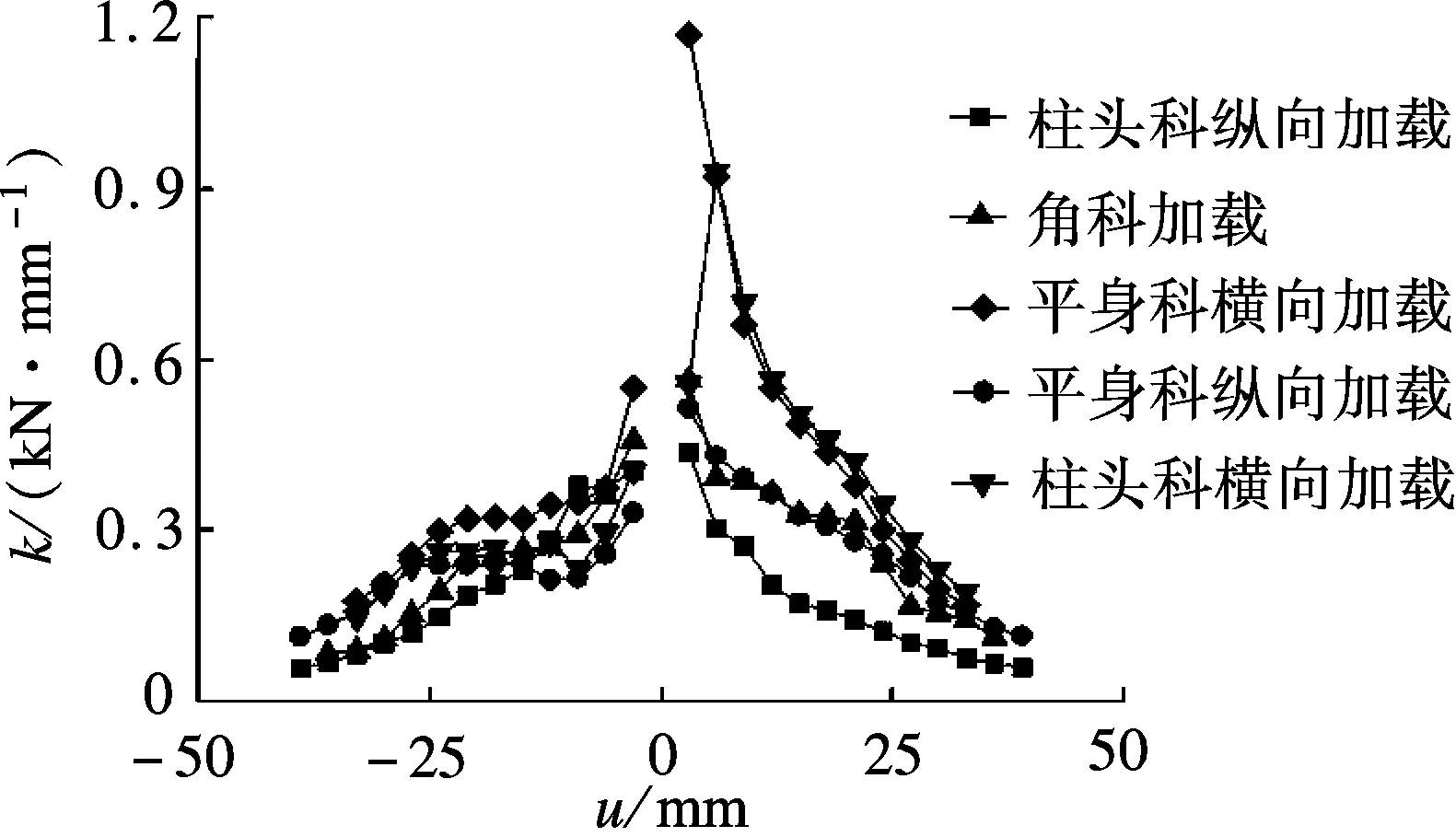
图12 太和殿二层斗拱k值退化曲线
3.6 水平刚度简化计算模型
基于图10所示的太和殿二层斗拱F-u骨架曲线,可归纳出其简化水平刚度简化计算模型(见图13).由图可知,曲线由3条折线段OA-AB-BC组成.其中,OA段的斜率对应于u=0~3 mm时斗拱的水平刚度k1,该阶段斗拱构件在外力作用下初步挤紧,斗拱处于正常受力状态.AB段的斜率对应于u=3~12 mm时斗拱的水平刚度k2,该阶段斗拱构件的咬合力随着u值的增大而增大,但增加幅度下降,斗拱k值略有减小,构件间因间距增大或少部分构件挤压变形而产生较为明显的摩擦力,斗拱处于近似屈服阶段,B点可认为是斗拱的近似屈服点.BC段的斜率对应于u=12~30 mm时斗拱的水平刚度k3,该阶段斗拱部分构件产生变形、破坏,斗拱构件间的挤压咬合作用明显减弱,k值明显减小,斗拱处于破坏阶段,C点可认为是斗拱的极限承载点.
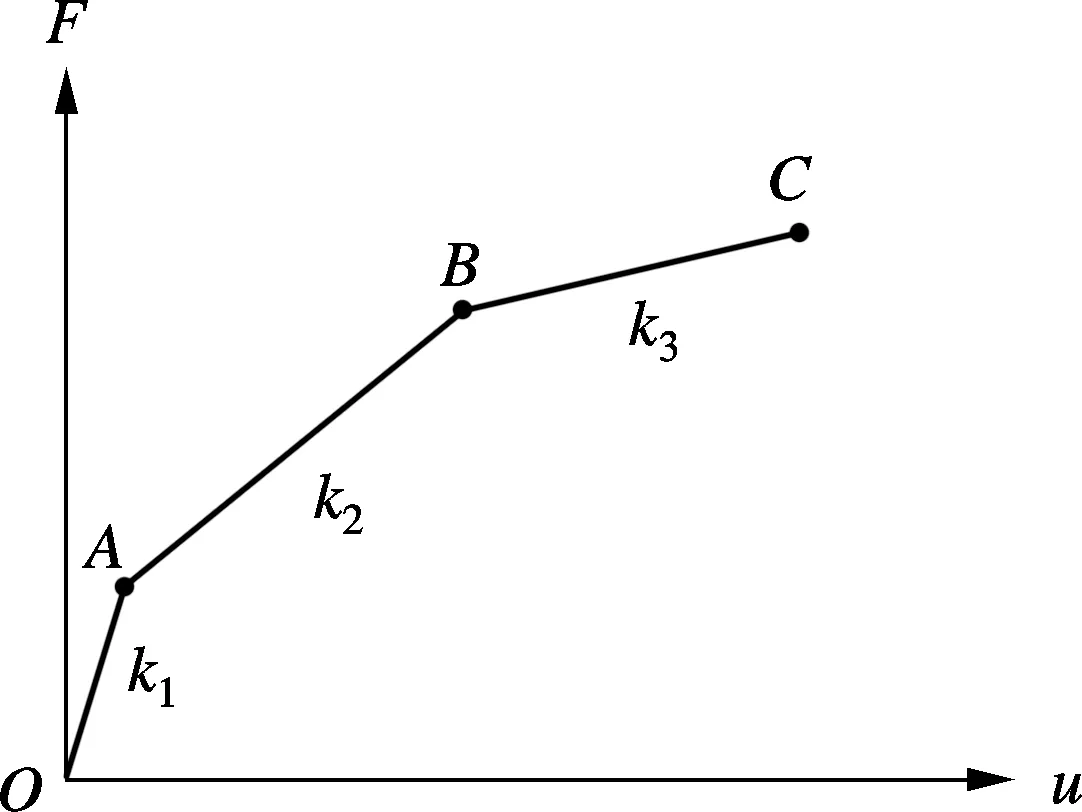
图13 太和殿二层斗拱水平刚度简化模型
斗拱在各受力阶段的水平刚度可表示为
(3)
(4)
(5)
式中,Fs,us分别为斗拱构件进入摩擦、挤压状态时的水平力和侧移.
根据图10和表2中的数据展开计算(取正反向加载结果的平均值),获得不同阶段各斗拱的k值.由表3可知,k1>k2>k3,说明斗拱在水平加载过程中存在一个刚度退化过程,即构件初步咬合—挤紧—松动—变形或破坏的受力状态发展过程.
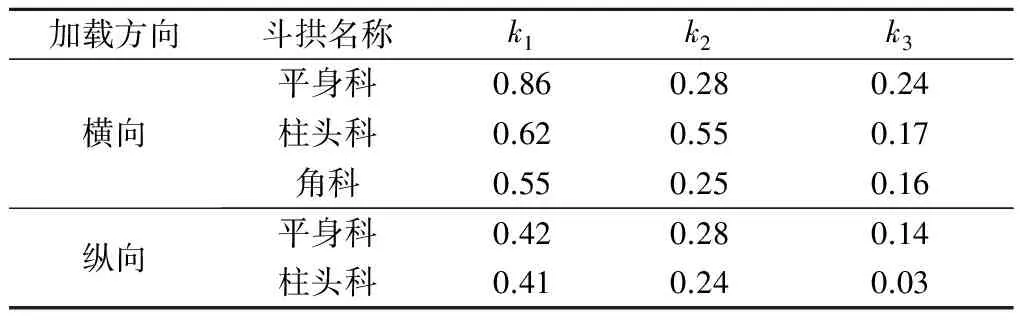
表3 斗拱水平刚度计算结果 kN/mm
在各受力阶段,各斗拱的水平刚度值由大到小的顺序为:平身科横向加载、柱头科横向加载、角科加载、平身科纵向加载、柱头科纵向加载.斗拱在横向受力时,各构件间的作用力以挤压、咬合为主,斗拱产生较小水平位移时所需荷载较大.斗拱在纵向受力时,各构件间的作用力以摩擦滑移为主.与横向加载相比,斗拱产生同等量水平位移时纵向加载所需的荷载要小得多.因此,斗拱在纵向加载时的水平刚度小于横向加载时的水平刚度.对于角科斗拱而言,其加载方向为斜向,斗拱构件间摩擦、挤压作用兼有,因而其刚度大小居中.在总尺寸相近的前提下,由于平身科斗拱数量远大于柱头科斗拱,构件间的作用力大于后者,因而无论采用哪种方式加载,使平身科斗拱产生单位侧移时所需的外力均大于后者.
4 结论
1) 水平低周反复荷载作用下,太和殿二层斗拱普遍出现变形及构架挤压吱声,且沿横向加载时相对于纵向加载更容易产生构件破坏.
2) 横向加载条件下,各斗拱的F-u滞回曲线形状表现为构件挤压作用较为明显的梭形或弓形;而纵向加载时,各斗拱F-u滞回曲线均表现为反映斗拱构件间存在摩擦滑移性能的反S形或Z形.斗拱自身恢复力均较差.
3) 横向加载条件下,柱头科斗拱水平承载性能优于平身科斗拱,角科斗拱的水平承载性能最差;纵向加载条件下,平身科斗拱水平承载性能优于柱头科斗拱,角科斗拱水平承载性能最好.
4) 同一加载条件下,柱头科斗拱的延性性能优于平身科斗拱;角科斗拱的延性性能相对前二者略差.
5) 横向加载条件下,柱头科的耗能能力优于平身科斗拱;纵向加载条件下,平身科斗拱的耗能性能优于柱头科;角科斗拱的耗能性能最好.
6) 同一加载条件下,平身科斗拱水平刚度退化比柱头科斗拱严重;角科斗拱水平刚度退化不明显.
7) 太和殿二层斗拱的水平刚度模型可简化为三折线段形式.
References)
[1]王效青. 中国古建筑术语辞典[M]. 太原:山西人民出版社, 1996:76-77.
[2]周乾,闫维明,纪金豹.明清古建筑木结构典型抗震构造问题研究[J].文物保护与考古科学,2011,23(2):36-48. Zhou Qian, Yan Weiming, Ji Jinbao. Typical aseismic construction problems in ancient Chinese wooden buildings of Ming and Qing dynasties[J].SciencesofConservationandArchaeology, 2011,23(2):36-48. (in Chinese)
[3]周乾, 闫维明, 慕晨曦, 等. 故宫太和殿一层斗拱竖向加载试验[J]. 西南交通大学学报, 2015, 50(5): 879-885. DOI:10.3969/j.issn.0258-2724.2015.05.017. Zhou Qian, Yan Weiming, Mu Chenxi, et al. Experimental investigation of bracket sets of 1st eave of Taihe Palace in the Forbidden City under vertical loads[J].JournalofSouthwestJiaotongUniversity, 2015, 50(5): 879-885. DOI:10.3969/j.issn.0258-2724.2015.05.017.(in Chinese)
[4]袁建力,施颖,陈韦,等.基于摩擦-剪切耗能的斗拱有限元模型研究[J].建筑结构学报,2012,33(6):151-157. Yuan Jianli, Shi Ying, Chen Wei, et al. Finite element model of dou-gong based on energy dissipation by friction-shear[J].JournalofBuildingStructures, 2012,33(6):151-157. (in Chinese)
[5]邵云,邱洪兴,乐志,等.宋、清式斗拱低周反复荷载试验研究[J].建筑结构,2014,44(9):79-82. Shao Yun, Qiu Hongxing, Yue Zhi, et al. Experimental study of low-cycle loading test on Song-style and Qing-style dougong [J].BuildingStructure, 2014, 44(9):79-82. (in Chinese)
[6]阙泽利,李哲瑞,张贝贝,等.明甪直天王殿松木斗拱振动台试验研究[J].土木建筑与环境工程,2015,37(3):26-34. DOI:10.11835/j.issn.1674-4764.2015.03.004. Que Zeli, Li Zherui, Zhang Beibei, et al. Experimental analysis on shaking table tests of dougong in Tianwang Hall, Luzhi, Ming dynasty [J].JournalofCivil,Architecture&EnvironmentalEngineering, 2015, 37(3):26-34. DOI:10.11835/j.issn.1674-4764.2015.03.004. (in Chinese)
[7]谢启芳,向伟,杜彬,等.古建筑木结构叉柱造式斗拱节点抗震性能试验研究[J].土木工程学报,2015,48(8):19-28. Xie Qifang, Xiang Wei, Du Bin, et al. Experimental study on seismic behavior of fork-column “Dougong” joints in timber structures of Chinese ancient buildings[J].ChinaCivilEngineeringJournal, 2015, 48(8):19-28. (in Chinese)
[8]Yeo S Y, Hsu M F, Komatsu K, et al. Shaking table test of the Taiwanese traditional Dieh-Dou timber frame[J].InternationalJournalofArchitecturalHeritage, 2015, 10(5): 539-557. DOI:10.1080/15583058.2015.1009574.
[9]津和佑子, 加藤圭,金惠園,等.組物有する伝統木造軸組の振動台実験[J].生産研究,2008,60(2):11-14.
[10]Fujita K, Sakamoto I, Ohashi Y, et al. Static and dynamic loading tests of bracket complexes used in traditional timber structures in Japan[C]//Proceedingofthe12thWorldConferenceonEarthquakeEngineering. Auckland, New Zealand, 2000:0851.
[11]Lee Y W, Hong S G, Bae B S, et al. Experiments and analysis of the traditional wood structural frame [CD]//Proceedingsofthe14thWorldConferenceofEarthquakeEngineering. Beijing: 2008.
[12]马炳坚.中国古建筑木作营造技术[M].北京:科学出版社,1991:237-239.
[13]崔瑾.太和殿斗拱构造浅析[C]//郑欣淼,晋宏逵.中国紫禁城学会论文集第八辑.北京:故宫出版社,2014:278-301.
[14]高大峰, 李飞, 刘静, 等. 木结构古建筑斗拱结构层抗震性能试验研究[J]. 地震工程与工程振动, 2014, 34(1): 131-139. DOI:10.13197/j.eeev.2014.01.131.gaodf.017. Gao Dafeng, Li Fei, Liu Jing, et al. Experimental study on the seismic performance of the structural layer with corbel bracket of ancient Chinese timber structure[J].EarthquakeEngineeringandEngineeringVibration, 2014, 34(1): 131-139. DOI:10.13197/j.eeev.2014.01.131.gaodf.017.(in Chinese)
[15]李忠献.工程结构试验理论与技术[M].天津:天津大学出版社,2003:228-234.
Experiments on seismic performance of bracket sets of second eave of Taihe Palace in the Forbidden City
Zhou Qian1,2Yang Na1Chun Qing3
(1School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China) (2Palace Museum, Beijing 100009, China) (3Key Laboratory of Urban and Architectural Heritage Conservation of Ministry of Education, Southeast University, Nanjing 211189, China)
To effectively protect Chinese ancient buildings, the low cyclic reversed loading tests of the bracket sets of the second eave of Taihe Palace in the Forbidden City were developed. The 1∶2 scaled models of the bracket sets were built. The transverse and longitudinal loadings were carried out to study the seismic parameters of the bracket sets. The results show that, compared to longitudinal loading, the bracket sets are more easily to be damaged under the transverse loading. For different types of the bracket sets, the descending order of the ultimate bearing capacity is the column set with transverse loading, the intermediate set with transverse loading, the corner set with loading, the intermediate set with longitudinal loading, the column set with longitudinal loading. The descending order of the ductility is the column set with longitudinal loading, the intermediate set with longitudinal loading, the column set with transverse loading, the corner set with loading, the intermediate set with transverse loading. The descending order of the energy dissipation capability is the corner set with loading, the column set with transverse loading, the intermediate set with longitudinal loading, the column set with longitudinal loading, the intermediate set with transverse loading. The descending order of the degradation degree of the level stiffness is the intermediate set with transverse loading, the column set with transverse loading, the corner set with loading, the intermediate set with longitudinal loading, the column set with longitudinal loading. The calculation model of the level stiffness of the bracket sets of the second eave of Taihe Palace can be simplified as 3-part polygonal lines.
Taihe Palace; bracket sets of the second eave; earthquake; ancient building
第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.026
2016-07-05. 作者简介: 周乾(1975—),男,博士,研究员,qianzhou627@126.com.
国家自然科学基金优秀青年基金资助项目(51422801)、国家自然科学基金资助项目(51178028)、北京市自然科学基金重点资助项目(8151003)、东南大学城市与建筑遗产保护教育部重点实验室开放课题资助项目(KUAL1605A).
周乾,杨娜,淳庆.故宫太和殿二层斗拱水平抗震性能试验[J].东南大学学报(自然科学版),2017,47(1):150-158.
10.3969/j.issn.1001-0505.2017.01.026.
TU366.2
A
1001-0505(2017)01-0150-09
