考虑滑移效应的体外预应力钢-混凝土组合梁自振频率分析

2017-02-21项贻强BishnuGuptGautam

东南大学学报（自然科学版） 2017年1期

关键词：静力实测值钢梁

项贻强邱政 Bishnu Gupt Gautam

(1浙江大学建筑工程学院, 杭州 310058)(2浙江大学唐仲英传感材料及应用研究中心, 杭州 310058)

考虑滑移效应的体外预应力钢-混凝土组合梁自振频率分析

项贻强1,2邱政1Bishnu Gupt Gautam1

(1浙江大学建筑工程学院, 杭州 310058)(2浙江大学唐仲英传感材料及应用研究中心, 杭州 310058)

为了研究滑移与体外预应力对钢-混凝土组合简支梁自振频率的影响,提出了适用组合梁自振频率计算的静力折减刚度法和动力刚度修正系数法．以一根跨径为5 m的钢-混凝土组合简支试验梁为研究对象,分别采用静力折减刚度法、动力刚度修正系数法及换算截面法计算梁的自振频率,并将计算值与试验实测值进行对比．结果表明,采用动力刚度修正系数法计算得到的体外预应力组合梁的自振频率更接近于实测值,采用静力折减刚度法和换算截面法计算得到的梁的自振频率与实测值之间存在较大误差．当体外预应力值为100 kN时,换算截面法和静力折减刚度法与实测值的误差分别为19.3%和7.9%,动力刚度修正系数法误差则仅为2.9%．

体外预应力;钢-混凝土组合梁;滑移;自振频率;动力刚度修正系数法

钢-混凝土组合梁能充分发挥混凝土的抗压性能和钢材抗拉性能,广泛应用于公路和铁路桥梁中．由于柔性剪力连接件的存在,在进行组合梁计算时,应考虑滑移的影响[1]．聂建国等[2]及王景全等[3]分别采用折减刚度法和组合系数法来研究钢-混凝土组合梁的静力行为．文献[4-8]的研究结果表明,计算组合梁动力行为时,不能简单地直接使用静力折减刚度来处理界面滑移．文献[9-10]指出施加体外预应力可提高梁的自振频率．

滑移和体外预应力单独作用时对组合梁动力特性有明显影响,因而有必要就两者共同作用下对组合梁动力性能的影响进行研究．本文以一简支直线型体外预应力钢-混凝土组合梁为例,推导出组合梁的基本动力方程,分析了滑移和体外预应力产生的共同效应．

1 静力折减刚度法

聂建国等[2]提出了适用于组合梁静力计算的折减刚度法,认为考虑滑移后组合梁的刚度可表示为

(1)

式中,E为组合梁等效弹性模量;ID为组合梁折减后的截面惯性矩;IF为组合梁的换算截面惯性矩;ξ为组合梁的刚度折减系数．

将折减后的截面刚度EID应用于体外预应力钢-混凝土组合梁自振频率计算中．根据梁的固有振动方程可得体外预应力作用下组合梁的弯曲振动微分方程为[11]

(2)

式中,y为竖向振动位移;x为沿梁长纵向距离;T为体外预应力值;Mp=Te为体外预应力对梁产生的弯矩,其中,e为偏心距;m为单位长度梁的质量;t为时间．

因预应力大小随振动不断变化,故可进一步将T和MP表示为

T=T0+ΔT

(3)

MP=(T0+ΔT)e

(4)

式中,T0为初始体外预应力值;ΔT为振动中体外预应力值的变化量．

将式(3)、(4)代入式(2)中可得

(5)

振动的最大位移ymax≪e,故ΔTy≪ΔTe,即ΔTy可以被忽略．因此,式(5)可简化为

(6)

ΔT与振动位移有关,根据文献[12]可知

(7)

式中,l为梁长;φ=[e2+4IF/(A(1+ξ))]l2,其中，A为换算截面面积.

将式(7)代入式(6)中,可以求得梁的固有频率为

(8)

式中,n为振动阶数;ψ为静力频率修正系数,且

(9)

采用静力折减刚度法计算组合梁自振频率时,组合梁的整体等效动刚度可以表示为

(10)

式中,Iseq为采用静力折减刚度法时的截面等效动惯性矩;ψ2/(1+ξ)为静力刚度修正系数．

2 动力刚度修正系数法

为进行模型分析,首先进行如下假设:① 忽略混凝土与钢梁间的掀起作用;② 混凝土与钢梁满足小变形假设;③ 忽略转动惯量与剪切变形;④ 栓钉的剪力沿梁长均匀分布,纵向单位长度剪切刚度Ks不变;⑤ 栓钉所受剪力与变形呈线性关系．

取组合梁一微段dx,分别对混凝土板与钢梁进行受力分析(见图1)．图中,Q1,M1,N1分别为作用于混凝土截面的剪力、弯矩和轴力;Q2,M2分别为作用于钢梁截面的剪力、弯矩;N2为作用于钢梁截面的轴力,大小与混凝土截面轴力相等,方向相反; δ为滑移位移;V为单位长度混凝土与钢梁之间的挤压力．

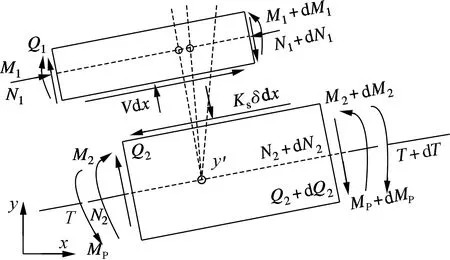
图1 组合梁微段受力分析图

根据图1,可得组合梁的基本动力微分方程为

(11)

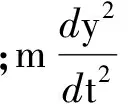
假设在dx的范围内,混凝土板与钢梁的转角为y′,则

δ=(y′-θ)h

(12)

不考虑竖向位移引起的梁体转动影响,由文献[6]可得

Ksh2(y′-θ)=EIGθ″

(13)

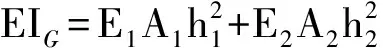
将式(3)、(7)、(12)、(13)代入式(11),经过化简可得

(14)

式中,EIF=EIG+EIB．

按文献[7]所述方法对式(14)进行求解,可得

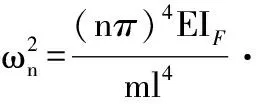
(15)

式中,α=EIC/(KSh2l)表示混凝土与钢梁之间的连接程度．

令γn为动力频率修正系数,且

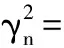
(16)

则有

(17)

组合梁的整体等效动刚度可表示为

(18)

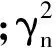
当抗剪强度Ks趋于无穷大(即混凝土与钢梁之间不考虑滑移)时,α趋于0,则动力刚度修正系数可化简为

(19)

由式(19)可知,动力刚度修正系数在形式上与不考虑滑移的体外预应力钢-混凝土组合梁修正系数一致．

3 算例

下面以文献[9]中跨径为5m的简支直线型体外预应力钢-混凝土组合梁为例进行分析与验证．分别采用换算截面法(TSM)、静力折减刚度(SRSM)和动力刚度修正系数法(DSMCM)计算该典型组合梁在不同预应力作用下的自振频率．其中,换算截面法忽略了混凝土板与钢梁之间的滑移,具体计算公式参见文献[9]．将基于这3种方法得到的计算结果与试验实测值进行比较,结果见表1和图2．

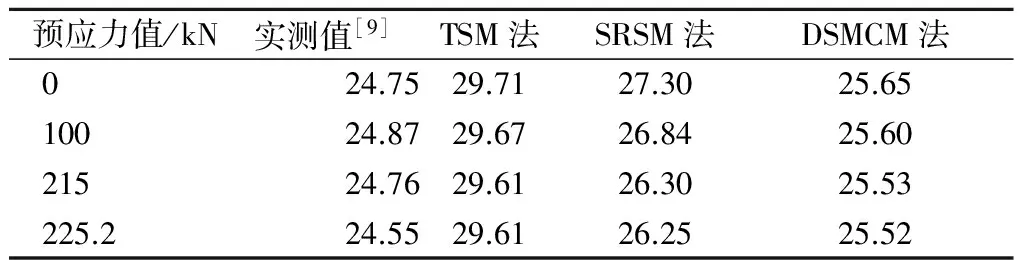
表1 第1阶自振频率实测值与计算值 Hz

图2 不同预应力作用下各计算值与实测值相对误差比较

由表1和图2可知,采用DSMCM法所得的频率与实测值最为吻合,而采用SRSM法和TSM法所得的频率均较实测值大．以预应力值100 kN的情况为例,基于TSM法、SRSM法、DSMCM法的计算值与实测值之间的误差分别为19.3%, 7.9%, 2.9%．因此,在进行体外预应力组合梁桥动力计算时,若忽略组合梁滑移效应或直接采用静力方法,将产生较大误差．

计算结果同时也表明,滑移效应将降低体外预应力组合梁的动力刚度,这与无预应力时钢-混凝土组合梁的结论一致．采用DSMCM法所得各预应力值下的频率均小于SRSM法,说明采用SRSM法将低估滑移对组合梁刚度折减的影响．

4 参数分析

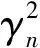
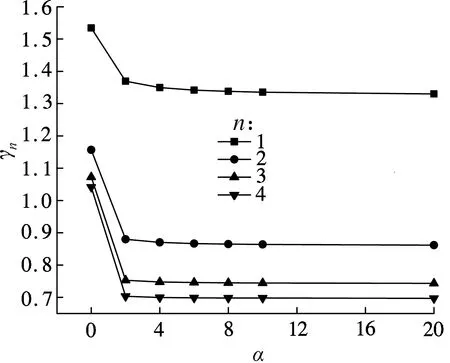
图3 预应力值为100 kN时α-γn关系图

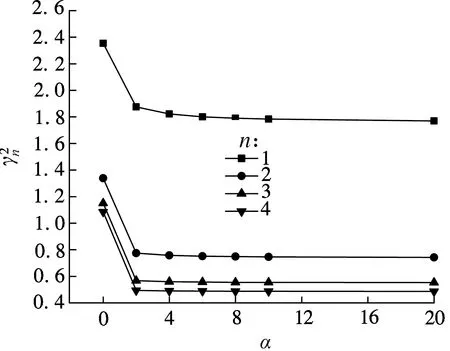
图4 预应力值为100 kN时α-γ2n关系图

文献[7]指出,对于无体外预应力的钢-混凝土组合梁桥,当α→0时,各阶动力频率折减系数均趋于1．由图3可以看出,在体外预应力的作用下,各阶动力频率修正系数不再趋于1,且差异较大,说明体外预应力对不同阶数的动力频率修正系数影响较大．

由图3还可以看出,当α→∞时,一阶频率修正系数的稳定值与其余各阶频率修正系数的稳定值差异较大，其中，γ1的稳定值大于1,γ2,γ3,γ4的稳定值均小于1,而文献[7]中各阶频率折减系数的稳定值均小于1,说明对于组合梁低阶的动力频率修正系数,体外预应力的增强作用比滑移的削弱作用大．

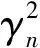
图5给出了不同自振阶数的情况下该典型组合梁的静力刚度修正系数与动力刚度修正系数的关系图．

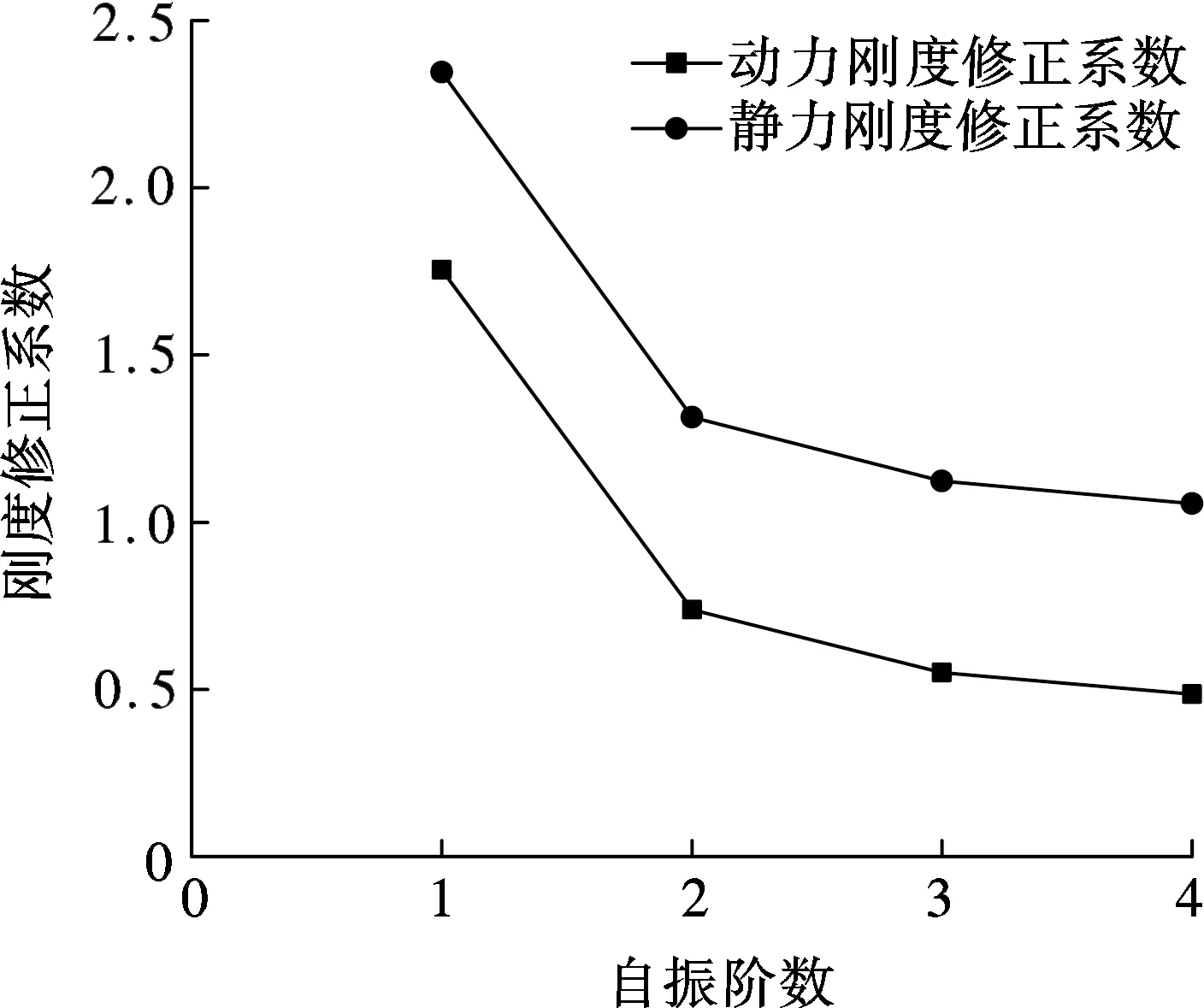
图5 前4阶自振阶数下静动力刚度修正系数比较

由图5可知,对于不同的自振阶数,静力刚度修正系数均大于动力刚度修正系数,且在前4阶,静力刚度修正系数均大于1,而动力刚度修正系数仅在第1阶时大于1,自第2阶后均小于1．说明采用静力刚度折减法计算钢-混凝土组合梁自振频率时将低估滑移对刚度的折减作用,且阶数越高,产生的误差越大．

5 结论

1) 体外预应力组合梁桥动力计算时,若忽略组合梁滑移效应或直接采用静力方法计算结构动力特性,将产生较大误差．

2) 体外预应力对组合梁不同阶数的动力频率修正系数影响较大,设计计算时应引起注意．

3) 对于组合梁低阶动力频率修正系数,体外预应力的增强作用比滑移的削弱作用大．

4) 对体外预应力钢-混凝土组合梁进行抗剪连接件损伤识别时,采用与刚度相关的检测指标较频率指标更有效．

5) 采用静力折减刚度法计算钢-混凝土组合梁动力特性时,将低估滑移对刚度的折减作用,且阶数越高,产生的误差越大．

References)

[1]何余良, 项贻强, 李少俊, 等. 基于不同抛物线翘曲函数组合箱梁剪力滞[J]. 浙江大学学报(工学版), 2014, 48(11): 1933-1940,1961. He Yuliang, Xiang Yiqiang, Li Shaojun, et al. Analysis on shear-lag effect of composite girders based on different parabolic warping displacement function[J].JournalofZhejiangUniversity(EngineeringScience), 2014, 48(11):1933-1940,1961. (in Chinese)

[2]聂建国, 沈聚敏, 余志武. 考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J]. 土木工程学报, 1995, 28 (6): 11-17. Nie Jianguo, Shen Jumin, Yu Zhiwu. A reduced rigidity method for calculating deformation of composite steel-concrete beams[J].ChinaCivilEngineeringJournal, 1995, 28(6): 11-17. (in Chinese)

[3]王景全, 吕志涛, 刘钊. 部分剪力连接钢-混凝土组合梁变形计算的组合系数法[J]. 东南大学学报(自然科学版), 2005, 35(S1): 5-10. DOI:10.3321/j.issn:1001-0505.2005.z1.003. Wang Jingquan, Lü Zhitao, Liu Zhao. Consistency factor method for calculating deformation of composite steel-concrete girders with partial shear connection[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2005, 35(S1): 5-10. DOI:10.3321/j.issn:1001-0505.2005.z1.003.(in Chinese)

[4]侯忠明, 夏禾, 张彦玲. 栓钉连接件抗剪刚度对钢-混凝土结合梁自振特性影响研究[J]. 中国铁道科学, 2012, 33(6): 24-29. DOI:10.3969/j.issn.1001-4632.2012.06.05. Hou Zhongming, Xia He, Zhang Yanling. The influence of the shear stiffness of stud connectors on the natural vibration characteristics of steel-concrete composite beams[J].ChinaRailwayScience, 2012, 33(6): 24-29. DOI:10.3969/j.issn.1001-4632.2012.06.05.(in Chinese)

[5]Berczyński S, Wróblewski T. Experimental verification of natural vibration models of steel-concrete composite beams[J].JournalofVibration&Control, 2010, 16(9): 2057-2081. DOI:10.1177/1077546309350552.

[6]张书兵, 王景全, 李明, 等. 考虑界面滑移效应的组合梁自振频率计算的修正折减刚度法[J]. 土木工程学报, 2015, 48 (12): 41-49. Zhang Shubing, Wang Jingquan, Li Ming, et al. A modified stiffness reduction method for calculating the natural frequencies of composite beams considering the effect of interfacial slippage[J].ChinaCivilEngineeringJournal, 2015, 48(12): 41-49. (in Chinese)

[7]侯忠明, 夏禾, 王元清, 等. 钢-混凝土组合梁动力折减系数研究[J]. 振动与冲击, 2015, 34(4): 74-81. DOI:10.13465/j.cnki.jvs.2015.04.014. Hou Zhongming, Xia He, Wang Yuanqing, et al. Dynamic reduction coefficients for a steel-concrete composite beam[J].JournalofVibrationandShock, 2015, 34(4): 74-81. DOI:10.13465/j.cnki.jvs.2015.04.014.(in Chinese)

[8]侯忠明. 钢-混凝土结合梁桥动力性能及损伤识别的理论分析与模型试验研究[D]. 北京: 北京交通大学土木工程学院, 2013.

[9]熊辉霞, 张耀庭. 体外预应力混凝土梁自振频率分析[J]. 工程力学, 2008,25(S2): 173-176. Xiong Huixia, Zhang Yaoting. Analysis of natural frequency of externally prestressed concrete beam [J].EngineeringMechanics, 2008, 25(S2): 173-176. (in Chinese)

[10]王常雷. 预应力钢-混凝土组合梁的动力特性研究[D]. 上海: 同济大学土木工程学院, 2008.

[11]Biscontin G, Morassi A, Wendel P. Vibrations of steel-concrete composite beams[J].JournalofVibrationandControl, 2000, 6(5): 691-714. DOI:10.1177/107754630000600503.

[12]郑尚敏, 马磊, 万水. 体外预应力对波形钢腹板箱梁自振频率的影响分析[J]. 东南大学学报(自然科学版), 2014, 44(1): 140-144. DOI:10.3969/j.issn.1001-0505.2014.01.025. Zheng Shangmin, Ma Lei, Wan Shui. Analysis on effects of externally prestressed tendons on vibration frequency of box girder with corrugated steel webs[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2014, 44(1): 140-144. DOI:10.3969/j.issn.1001-0505.2014.01.025.(in Chinese)

Analysis on natural frequencies of steel-concrete composite beam with external prestressed tendons considering slip effects

Xiang Yiqiang1,2Qiu Zheng1Bishnu Gupt Gautam1

(1College of Civil and Architectural Engineering, Zhejiang University, Hangzhou 310058, China) (2Cyrus Tang Center for Sensor Materials and Applications, Zhejiang University, Hangzhou 310058, China)

To study the influence of the slip and the external prestressed tendons on the natural frequencies of the simply-supported steel-concrete composite beam, the static reduced stiffness method(SRSM) and the dynamic stiffness modified coefficient method(DSMCM) were proposed. Taking a simply-supported steel-concrete composite experimental beam with the span of 5 m as a research object, the natural frequencies of the beam were calculated by the proposed SRSM, the DSMCM and the transformed section method(TSM), respectively. The calculation results were compared with the dynamic test results. The results show that the natural frequencies of the steel-concrete composite beam with the external prestressed tendons calculated by the proposed DSMCM are closer to the dynamic test results,while those predicted by the SRSM and the TSM exhibit big errors. When the external prestressing is 100 kN, the errors of the TSM and the SRSM are 19.3% and 7.9%, respectively, while that of the DSMCM is only 2.9%.

external prestressed tendon; steel-concrete composite beam; slip; natural frequency; dynamic stiffness modified coefficient method