泡沫铝和石蜡复合相变材料的传热特性分析

2017-02-21黄欣鹏唐超权陈振乾

东南大学学报（自然科学版） 2017年1期

关键词：石蜡热流低密度

黄欣鹏唐超权施娟陈振乾

(1东南大学能源与环境学院, 南京 210096)(2东南大学建筑设计研究院, 南京 210096)

泡沫铝和石蜡复合相变材料的传热特性分析

黄欣鹏1唐超权2施娟1陈振乾1

(1东南大学能源与环境学院, 南京 210096)(2东南大学建筑设计研究院, 南京 210096)

通过将融化的石蜡注入泡沫铝构成复合相变材料,能有效改善复合相变材料石蜡的导热性能.以两边定壁温、两边绝热的正方形泡沫铝复合石蜡相变材料为研究对象,利用双温度模型分析了纯石蜡、低密度泡沫铝复合石蜡、高密度泡沫铝复合石蜡的传热特性.采用相似理论得出双温度模型的理论解形式,并以显热容法数值模拟了相变传热过程.结果表明:经过简化的双温度模型的理论解与数值解高度吻合,在正方形中二维传热可以简化为一维传热来进行求解;泡沫铝复合石蜡相变材料的导热系数比纯石蜡有了较大改善;相变过程中石蜡和泡沫铝之间的温度差不可忽略.

复合相变材料;泡沫铝;双温度模型;显热容法;相似理论;有限容积法

利用相变材料存储能量可实现能量的时间和空间转换.由于相变过程近似等温,易于控制储能系统的温度,因此相变储能有很好的应用前景[1].

采用多孔介质和相变材料复合而成的复合相变材料可以利用多孔介质良好的导热网络结构形式来强化相变材料的传热过程.在生态建筑上,复合相变材料被用来吸收和释放热量以便对室内环境进行热调节[2].

施娟等[3]利用多孔介质相变传热显热容法模型研究了肿瘤冻融过程,研究了冷热交替作用下生物组织中的温度场变化规律.戴晓丽等[4]将多孔介质相变传热应用于石蜡/聚乙烯相变胶囊研究中,分析了相变材料的体积变化和斯蒂芬数对相变凝固时间的影响.程文龙等[5]以泡沫铝为研究对象,给出了多孔介质当量热导率的计算方法,利用准稳态方法建立了复合相变材料凝固过程的数学模型,并对其凝固过程的传热特性进行了理论分析.

Krishnan等[6]用双温度模型对泡沫金属中水流动和传热特性进行了数值分析,并指出对于泡沫金属空气或泡沫金属相变材料系统,在典型的Ra数和Da数范围内,固相响应较快;当Nuf<1时,应采用双温度模型.Saeid等[7]同样研究了方腔多孔介质中稳态自然对流的问题,并指出黏性耗散效应减慢了热传递的速率,随着表征黏性耗散效应参数值的不断增加,多孔方腔内平均Nu数不断减少.Deleglise等[8]用实验的方法研究了纤维介质中非等温树脂流动的温度分布.Hayes等[9]分别采用二维数值计算模型和FluentTM软件多孔介质模型研究了矩形热交换器内对流换热的问题,并对多孔介质非平衡换热模型进行了实验验证.Malashetty等[10]使用解析求解方法对正方形区域底部加热、顶部冷却的泡沫多孔介质内流动和换热情况进行了理论分析.Nouri-Borujerdi等[11]分析了半无限大的多孔介质空间受底部热流诱导发展热边界层的稳定性.Harris等[12]研究了方腔多孔介质内的相变现象,发展了一种近似焓法理论模型和近似双温度理论模型.

目前,Jamal-Abad等[13]使用摄动法对多孔介质太阳能空气热交换器内的换热现象进行了分析,讨论了孔隙形状参数s、福希海默数F和热辐射参数ζ对集热效率的影响.Islam等[14]研究了在外加磁场条件下多孔介质内周期性振荡流的传热问题;通过简化达西动量项和能量方程并进行摄动分析,得出了流体温度和速度的理论表达式.Chen等[15]使用频谱配点法研究了方腔多孔介质内自然对流换热的问题,建立了该问题的局部平衡模型和局部非平衡模型,研究结果显示频谱配点方法得出的结果与该问题标准解一致.

由于泡沫金属复合相变材料内部的传热过程比单一介质中相应的传热过程复杂,目前人们对泡沫金属内固液相变传热过程中的机理了解尚不够清晰,缺乏理论方面的分析.本文根据泡沫金属复合相变材料传热的双温度模型,应用相似理论方法给出了问题的解析解形式,并应用显热容法模拟了该传热过程.研究了泡沫金属孔隙率对传热过程的影响,对泡沫金属和相变材料石蜡的温度分布进行了分析讨论.

1 理论模型

本文采用了方框泡沫铝骨架模型,方腔结构是微通道散热装置的一种主要形式,目前已有大量类似的产品. 融化石蜡复合方腔泡沫铝的模型如图1所示.方腔边长为l,左壁面温度为Th,右壁面温度为Tc,且满足Th>Tc(即从左壁面吸热右壁面放热);同时上下壁面保持绝热.为了简化控制方程,做如下假设:

1) 相变时忽略石蜡相变前后的体积变化;

2) 在固相和液相区石蜡和泡沫铝热物性保持不变;

3) 在多孔介质传热过程中忽略石蜡相变时的对流效应.

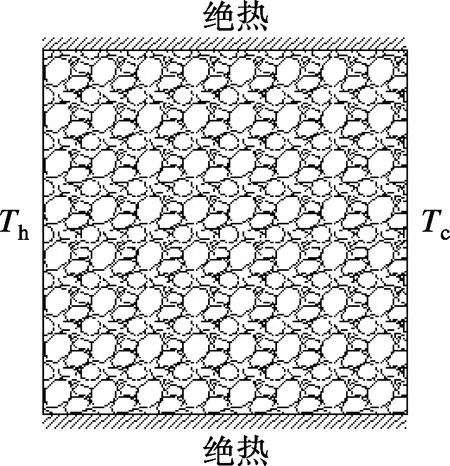
图1 方腔复合相变材料传热模型

泡沫金属和石蜡中的温度变化方程为

(1)

(2)

式中,ε为方腔泡沫金属的孔隙率;ρ为密度;c为比热容;k为导热系数;λ为石蜡和泡沫铝之间的等效换热系数;S为孔隙换热面积;V为孔隙体积;T为温度;下标f表示相变材料为石蜡;下标s表示泡沫铝骨架;下标REV表示表征体积单元.

比较式(1)和式(2)可知:式(1)等号右边最后一项带正号,式(2)等号右边最后一项带负号,说明其作用正好相反.此项是双温度模型的关键,此项数值相同而符号相反表示泡沫金属和石蜡间温差是泡沫金属和石蜡之间热量交换的原因.传统的单温度模型没有这一项,因此无法表现复合相变材料的传热特性.

由于式(1)和式(2)中未知变量Tf和Ts互相耦合,需要同时联立2个方程才能求解,故首先对方程解的形式进行分析.采用相似理论可以在不必求解具体方程时先得出结论解的特征.根据相似理论和量纲分析法,引入热扩散系数a=k/(ρc)和特征尺度l=VREV/SREV,则式(1)、式(2)简化为

Tf=f(ε,af,t,λ,l,Ts)

(3)

Ts=f((1-ε),as,t,λ,l,Tf)

(4)

由于ε为孔隙率,没有单位,设ε=mf/(ms+mf).其中,mf和ms分别为石蜡和泡沫铝的质量.由分析可知:当ε→0或ε→1时,即方腔空间内为纯泡沫铝或纯石蜡,此时由于石蜡和泡沫铝之间的换热量很小,可忽略石蜡和泡沫铝之间的换热项.讨论式(3)、(4)中的其他物理量,得到如下关系式:

(5)

(6)

从而得到解的形式为

(7)

分析式(7)可知:温度T仅与特征尺度l有关,与方腔空间的长宽无关,从而可以把该模型的二维传热问题简化为一维传热问题进行求解处理.

采用显热容法求解石蜡在泡沫铝孔隙中的相变过程,在固相、液相和糊状区域,相变材料的热容和导热系数分布函数[16]可表示为

(8)

(9)

式中,C为比热容, J/(kg·K);L为潜热, kJ/kg;ΔT为相变发生温度区间,K;下标g表示固态;下标y表示液态;下标m表示相变点.

2 数值模拟

数值模拟所用石蜡和泡沫铝的热物性见表1.石蜡相变温度Tm为333 K,相变发生温度区间ΔT为2 K.方腔边长l=0.1 m,方腔左壁面温度Th为333 K,右壁面温度Tc为353 K.

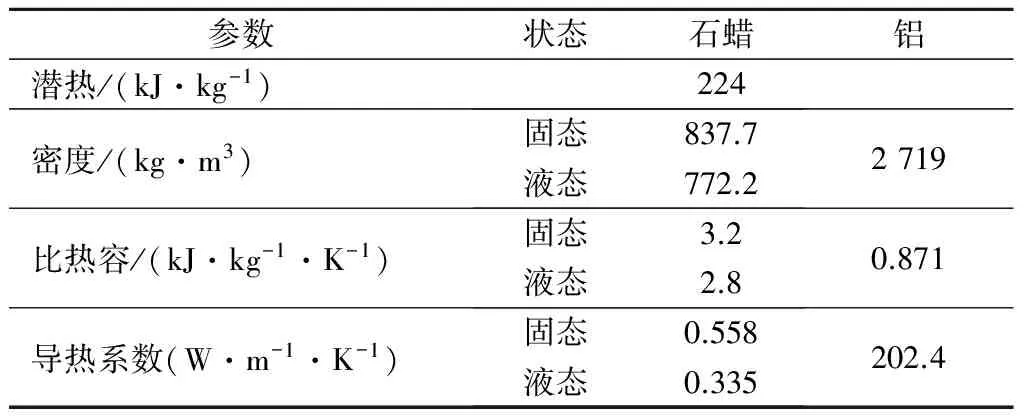
表1 材料的热物理性质

采用SIMPLE算法对问题进行计算,首先将方腔区域离散为正交网格的有限容积,计算时间步长取为1 s,当循环计算的残差小于10-5时,停止计算.

3 结果与讨论

3.1 纯石蜡和泡沫铝复合石蜡相变材料传热特性分析

图2为方腔内装满纯石蜡时方腔中心温度随时间的变化关系.由图可见,整个过程分为Ⅰ、Ⅱ、Ⅲ三个阶段.阶段Ⅰ为石蜡相变融化阶段,该阶段温度基本保持不变,持续时间约175 s;阶段Ⅱ为不规则情况阶段,在该阶段石蜡温度稳步攀升,该阶段温度受初始温度分布影响较大;阶段Ⅲ为充分发展阶段,在这一阶段方腔内各点温度不再受初始温度的影响,而取决于左、右壁面温度,并保持恒定不变,该阶段的开始时间约为1 350 s.

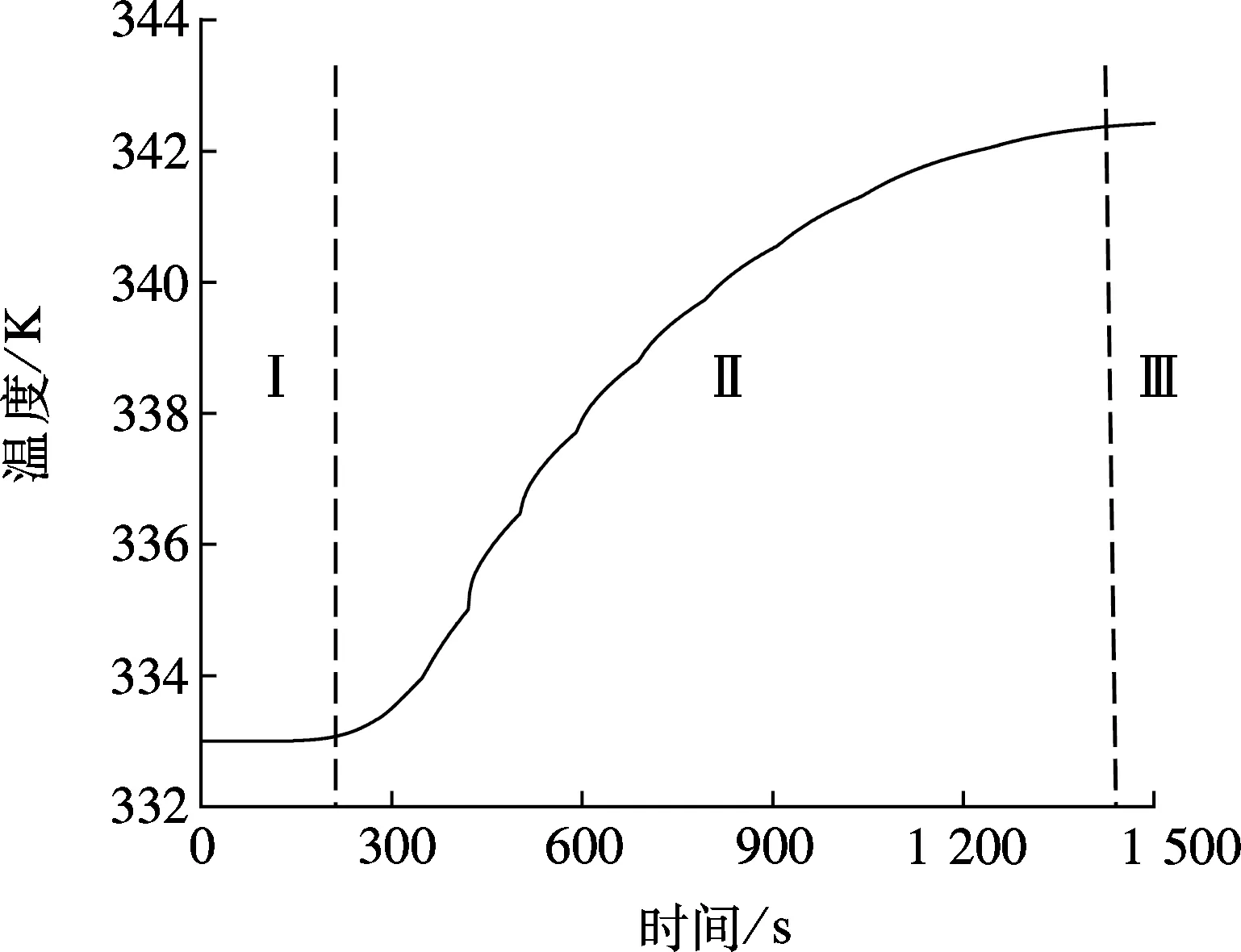
图2 方腔中心纯石蜡温度随时间变化曲线图

图3为纯石蜡在方腔内部的温度分布和温度随时间变化关系.从图3可以看出,纯石蜡温度从非稳态导热的L形曲线逐渐向稳态导热的直线转变.约在1 200 s时方腔内温度和到达稳态时温度之差已经缩小至1 K范围内.图4为与图3对应的左、右壁面热流变化曲线,从图4可以看出,初始时刻右壁面热流值最高,以后逐渐降低;左壁面热流值在600 s之前几乎为0,以后逐渐攀升;当达到稳态导热状态时,左、右壁面热流值相等.

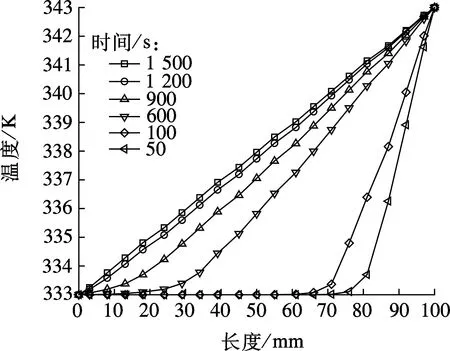
图3 不同时刻纯石蜡在方腔内部温度分布变化图

图4 纯石蜡左、右壁面热流随时间变化图

图5为低密度泡沫铝复合石蜡相变材料和高密度泡沫铝复合石蜡相变材料在方腔中心点的温度随时间变化曲线.从图5中可以看出,低密度泡沫铝复合石蜡相变材料的相变过程较高密度泡沫铝复合石蜡相变材料的相变过程长.这是因为在复合相变材料中相变材料所占比重越大,相变过程温度保持恒定的特征越明显.当高密度泡沫铝复合石蜡相变材

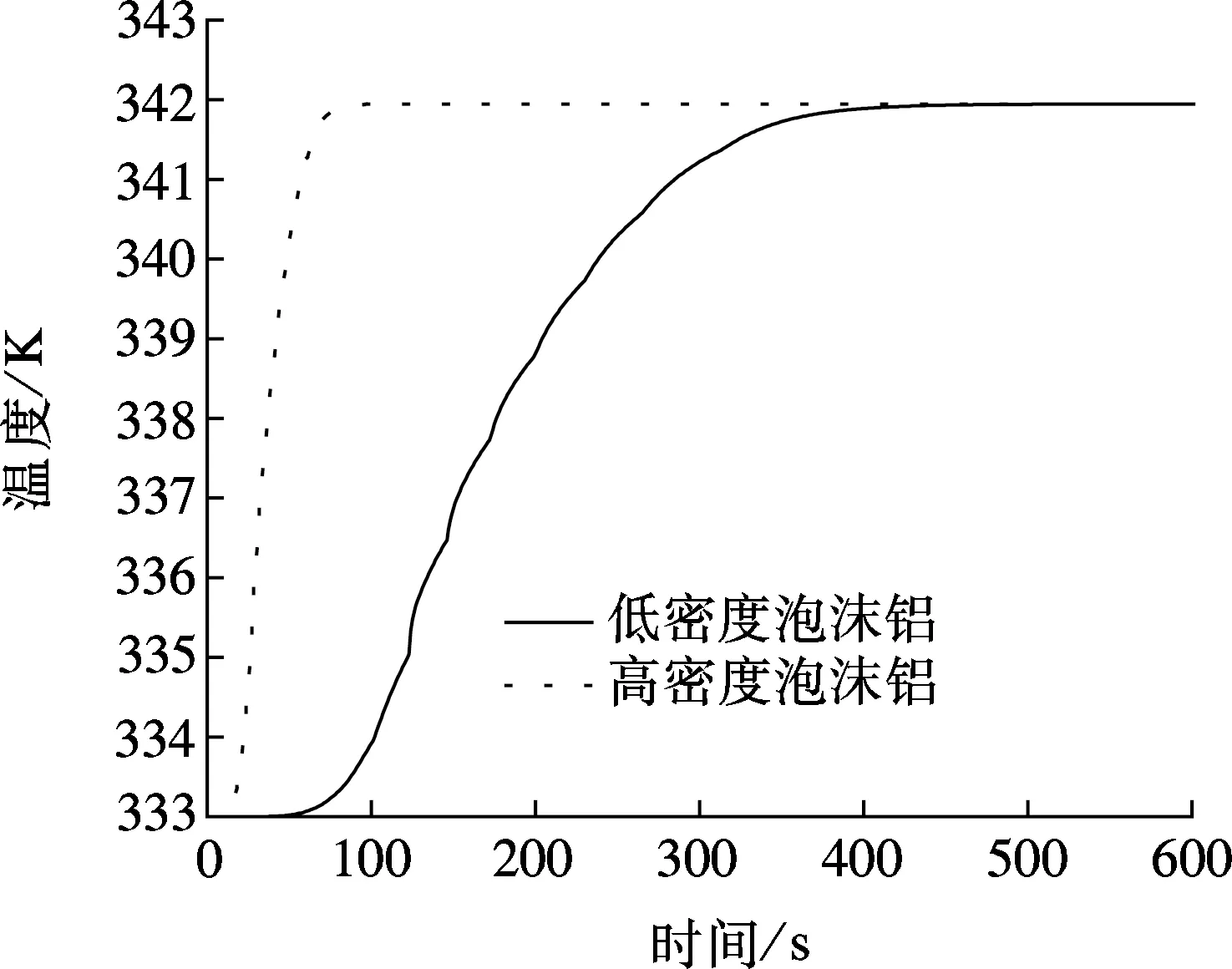
图5 方腔中心复合相变材料温度随时间变化曲线图

料已经达到稳态导热阶段时,低密度泡沫铝复合石蜡相变材料才结束相变过程,这说明复合相变材料中导热系数大的泡沫铝加快了非稳态导热过程的速率.当两者都进入稳态导热阶段时,两者温度曲线重合并保持不变.

高密度泡沫铝复合石蜡相变材料和低密度泡沫铝复合石蜡相变材料左、右壁面的热流分布如图6所示.

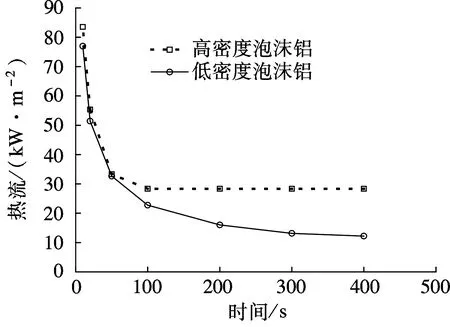
(a) 右壁面热流

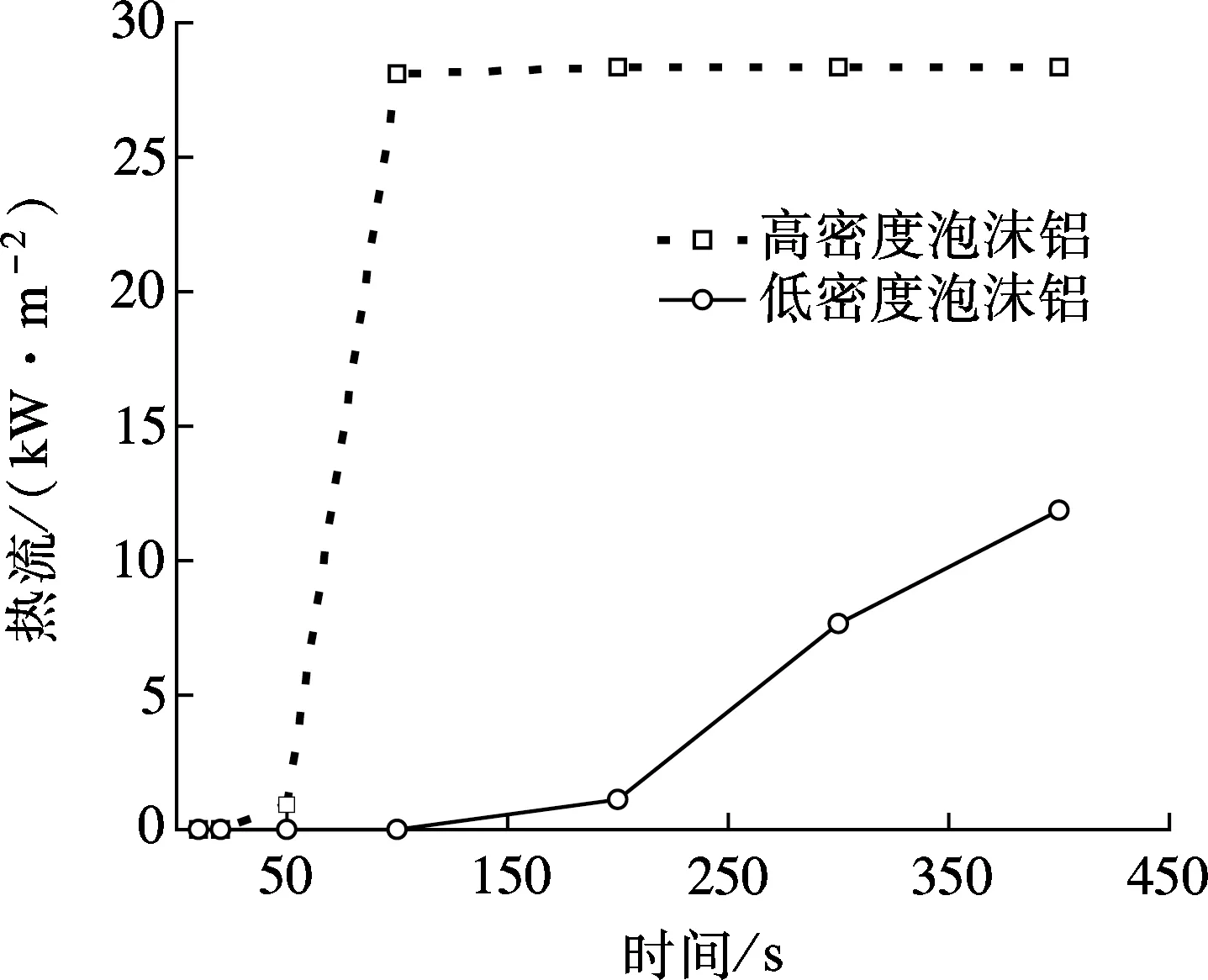
(b) 左壁面热流

由图6(a)可见,高密度泡沫铝复合石蜡与低密度泡沫铝复合石蜡在初始时刻位于右壁面处热流几乎相等.随着时间的推移,进入稳态导热阶段后,在右壁面处高密度泡沫铝复合石蜡的热流密度是低密度泡沫铝复合石蜡的2倍左右.同时高密度泡沫铝复合石蜡右壁面热流随时间变化曲线比低密度泡沫铝复合石蜡右壁面热流随时间变化曲线更陡.

由图6(b)可见,在初始时刻,无论是高密度泡沫铝复合石蜡还是低密度泡沫铝复合石蜡,通过左壁面传出的热流密度都为0.但低密度泡沫铝复合石蜡相变材料热流密度为0的时间段比较长;而高密度泡沫铝复合相变材料热流密度为0的时间段非常短.主要原因是在非稳态导热阶段,相变材料的作用表现为增大复合相变材料的热容.当进入稳态导热阶段后,由于高密度泡沫铝的热导率比低密度泡沫率的热导率高,透过左壁面传递的高密度泡沫铝石蜡相变材料的热流比低密度泡沫铝石蜡相变材料高.

3.2 理论解形式和数值解的比较

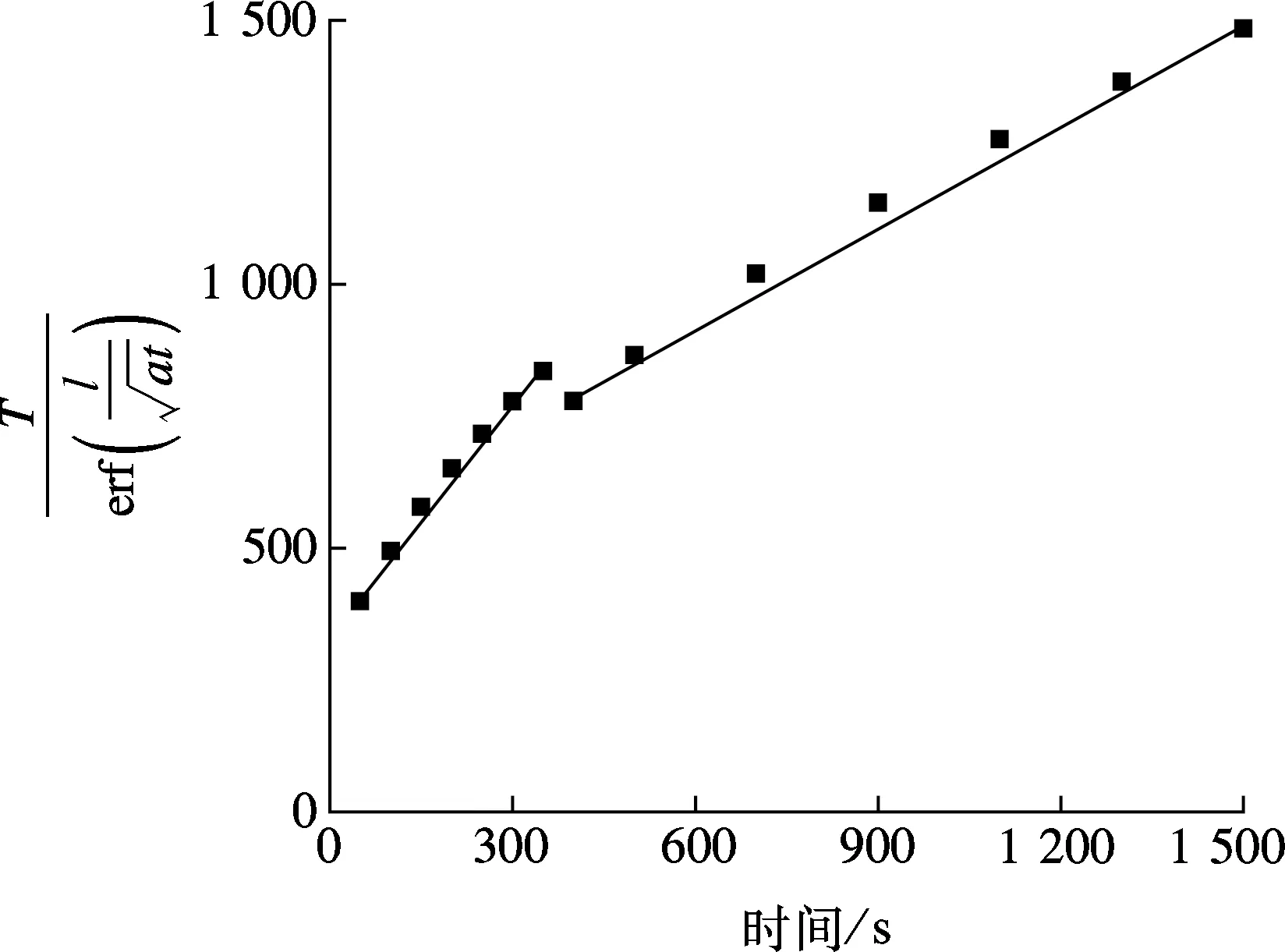
(a) 特征解lat

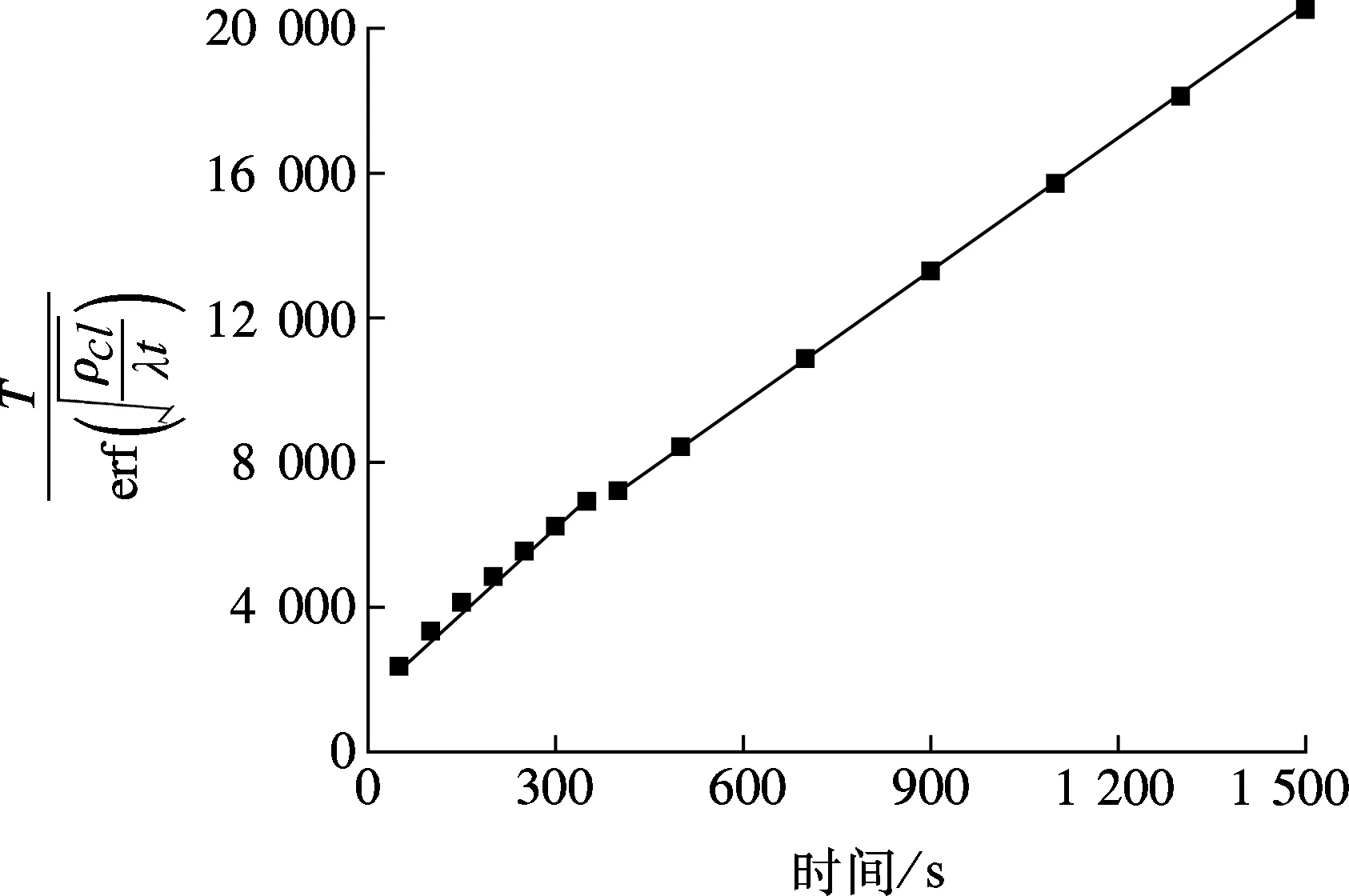
(b) 特征解ρclλt

3.3 双温度模型泡沫铝与石蜡之间温度差分析

图8(a)和(b)分别为低密度泡沫铝复合石蜡相变材料和高密度泡沫铝复合石蜡相变材料内石蜡与铝之间的温差在方腔内的分布.

由图8可见,由于石蜡和泡沫铝的热导率相差较大,表现为初始时刻石蜡和泡沫铝之间的温差最大,随着时间的推移温差逐渐变小.由图8还可以看出,在前100 s时间内,石蜡和泡沫铝之间的温差均在10 K以上,这表明在传热的初始阶段石蜡和泡沫铝之间的热交换不可忽略.

由图8(a)可见,在100 s时刻,位于方腔左半边的低密度泡沫铝和石蜡之间温差为0,这表明在100 s时刻方腔左半边的石蜡还未开始熔化,这从图5和图6(b)可以得到印证.

由图8(b)可见,在100 s时刻,方腔内泡沫铝和石蜡之间温差先达到最高峰,然后在方腔左半边呈近似直线下降趋势,这表明在100 s时已经进入石蜡和泡沫铝稳态换热的阶段.从图5、图6中也可看出,此时方腔左、右壁面已经进入稳态导热阶段.在20 s时,方腔左半边高密度泡沫铝和石蜡之间的温差为0,这表明在20 s时刻方腔左半边高密度泡沫铝复合石蜡还未开始熔化,这也可从图5和图6(b)得到印证.

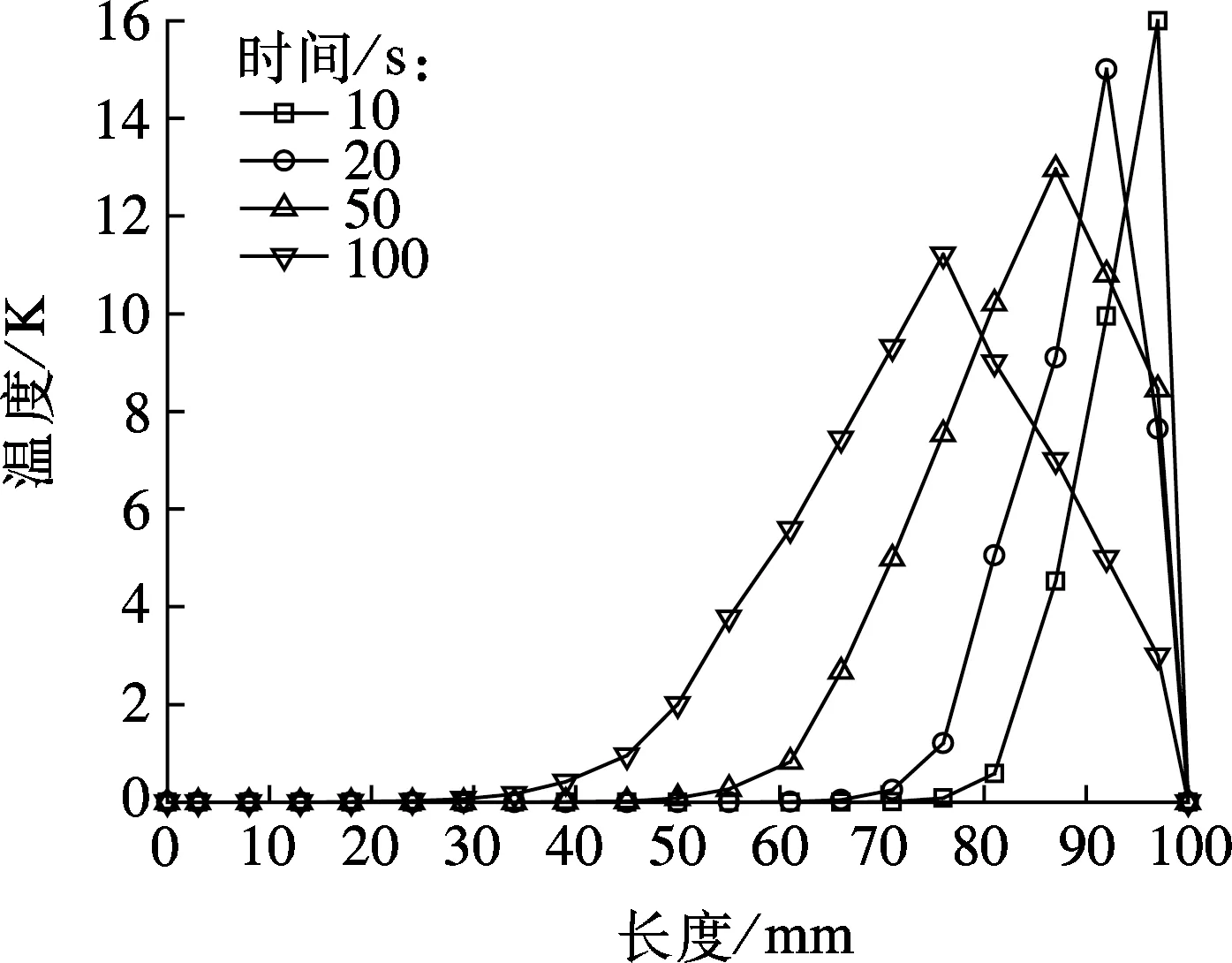
(a) 低密度泡沫铝

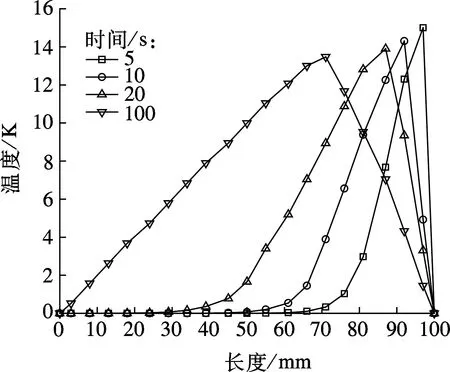
(b) 高密度泡沫铝

4 结论

1) 使用双温度模型计算的结果表明石蜡和泡沫铝之间的温差不可以忽略.

2) 向石蜡中添加泡沫铝构成复合相变材料可以有效地增大壁面热流;当进入充分发展阶段,在左、右壁面恒定温差条件下,壁面热流保持恒定不变.

3) 通过相似理论分析得出了相变传热问题的解析解特征形式,并通过数值解计算结果进行了验证.相似理论的解形式表明二维泡沫铝复合相变问题仅与孔隙尺度有关,故该二维问题可以简化为一维问题考虑.

References)

[1]张寅平,胡汉平,孔祥东,等.相变储能——理论和应用[M].合肥:中国科学技术大学出版社,1996：1-3.

[2]Gutierrez M P, Lee L P. Multiscale design and integration of sustainable building functions [J].Science, 2013, 341(6143): 247-248. DOI:10.1126/science.1237278.

[3]施娟,陈振乾,施明恒,等.肿瘤冻融相变传热过程的数值模拟[J].工程热物理学报,2008,29(6):1017-1020. Shi Juan, Chen Zhenqian, Shi Mingheng, et al. Numerical simulation on freezing and thawing phase change heat transfer process in tumor [J].JournalofEngineeringThermophysics, 2008, 29(6): 1017-1020. DOI: 10.3321/j.issn:0253-231X.2008.06.030. (in Chinese)

[4]戴晓丽,王登云,陈振乾,等.球形相变胶囊内凝固传热过程数值模拟[J].工程热物理学报,2013,34(4):715-719. Dai Xiaoli, Wang Dengyun, Chen Zhenqian, et al. Numerical simulation on solidification heat transfer of spherical phase change capsule [J].JournalofEngineeringThermophysics, 2013, 34(4): 715-719. (in Chinese)

[5]程文龙,韦文静.高孔隙率泡沫金属相变材料储能、传热特性[J].太阳能学报,2007,28(7):739-744. Cheng Wenlong, Wei Wenjing. Theoretical analysis of phase change material storage with porosity metal foams [J].ActaEnergiaeSolarisSinica, 2007, 28(7): 739-744. DOI: 10.3321/j.issn:0254-0096.2007.07.010.(in Chinese)

[6]Krishnan S, Murthy J Y, Garimella S V. A two-temperature model for the analysis of passive thermal control systems [J].JournalofHeatTransfer, 2004, 126(4): 628-637. DOI:10.1115/1.1773194.

[7]Saeid N H, Pop I. Viscous dissipation effects on free convection in a porous cavity [J].InternationalCommunicationsinHeatandMassTransfer, 2004, 31(5): 723-732. DOI: 10.1016/s0735-1933(04)00059-4.

[8]Deleglise M, Binetruy C, Castaing P, et al. Use of non local equilibrium theory to predict transient temperature during non-isothermal resin flow in a fibrous medium [J].InternationalJournalofHeatandMassTransfer, 2007, 50(11): 2317-2324. DOI:10.1016/j.ijheatmasstransfer.2006.10.020.

[9]Hayes A M, Khan J A, Shaaban A H, et al. The thermal modeling of a matrix heat exchanger using a porous medium and the thermal non-equilibrium model [J].InternationalJournalofThermalSciences, 2008, 47(10): 1306-1315. DOI:10.1016/j.ijthermalsci.2007.11.005.

[10]Malashetty M S, Shivakumara I S, Kulkarni S. The onset of Lapwood-Brinkman convection using a thermal non-equilibrium model [J].InternationalJournalofHeatandMassTransfer, 2005, 48(6): 1155-1163. DOI:10.1016/j.ijheatmasstransfer.2004.09.027.

[11]Nouri-Borujerdi A, Noghrehabadi A R, Rees D A S. The linear stability of a developing thermal front in a porous medium: The effect of local thermal non-equilibrium [J].InternationalJournalofHeatandMassTransfer, 2007, 50(15): 3090-3099. DOI:10.1016/j.ijheatmasstransfer.2007.01.005.

[12]Harris K T, Haji-Sheikh A, Agwu Nnanna A G. Phase-change phenomena in porous media: A non-local thermal equilibrium model [J].InternationalJournalofHeatandMassTransfer, 2001, 44(8): 1619-1625. DOI: 10.1016/s0017-9310(00)00191-5.

[13]Jamal-Abad M T, Saedodin S, Aminy M. Heat transfer in concentrated solar air-heaters filled with a porous medium with radiation effects: A perturbation solution [J].RenewableEnergy, 2016, 91: 147-154. DOI:10.1016/j.renene.2016.01.050.

[14]Islam S, Biglarbegian M, Mahmud S. Influence of magnetic field on the periodically oscillating fluid inside a porous medium attached to a thick solid plate [J].InternationalJournalofHeatandMassTransfer, 2016, 96: 602-613. DOI:10.1016/j.ijheatmasstransfer.2016.01.063.

[15]Chen Y Y, Li B W, Zhang J K. Spectral collocation method for natural convection in a square porous cavity with local thermal equilibrium and non-equilibrium models [J].InternationalJournalofHeatandMassTransfer, 2016, 96: 84-96. DOI:10.1016/j.ijheatmasstransfer.2016.01.007.

[16]郭宽良,孔祥谦,陈善年.计算传热学[M].合肥:中国科学技术大学出版社,1988:68-69.

Heat transfer characteristics on composite phase change materials filled with foamed aluminum and paraffin wax

Huang Xinpeng1Tang Chaoquan2Shi Juan1Chen Zhenqian1

(1School of Energy and Environment, Southeast University, Nanjing 210096, China) (2Architectural Design and Research Institute, Southeast University, Nanjing 210096, China)

By pouring the melting paraffin into foamed aluminum, the composite phase change material phase change material (PCM) was constructed and the thermal conductivity of PCM was greatly improved. The square shape composite PCM with constant temperature on two sides and adiabatic boundary on another two sides was selected as a research object. Heat-transfer characteristics of pure paraffin, low density foamed aluminum PCM, high density foamed aluminum PCM were analyzed using the two-temperature model. The form of the analytical solution of the two-temperature model was deduced by the similarity theory. The numerical modeling of the heat-transfer process was made by using the apparent heat capacity method. The results show that the theoretical resolution form of the simplified two-temperature model is highly consistent with the numerical solution. Also, two-dimensional heat transfer can be simplified as one-dimensional heat transfer in the square shape. In addition, the heat conductivity coefficient of foamed aluminum PCM is highly improved compared with the pure paraffin. The temperature difference between the paraffin and the foamed aluminum in the phase change process cannot be ignored.

composite phase change material (PCM); foamed aluminum; two-temperature model; apparent heat capacity method; similarity theory; finite volume method