基于MATLAB的语音信号去噪方法应用

韩长军

(辽东学院 信息工程学院，辽宁 丹东 118003 )



【信息科学与工程】

基于MATLAB的语音信号去噪方法应用

韩长军

(辽东学院 信息工程学院，辽宁 丹东 118003 )

以MATLAB为平台，利用滤波器去噪方法对含噪声的语音信号进行去噪处理，并从频域角度利用IIR和FIR两种滤波器去噪方法进行去噪，并对结果进行了对比分析，为加强程序的友好性和可视性，采用GUI编程的方法设计了语音信号去噪系统用户界面。实验结果证明，该方法能够实现对夹杂噪声的语音信号进行有效提取，有助于在噪声下提取微弱信号的研究。

语音信号；MATLAB；滤波器；去噪；频域

语言是人们获得各类有效信息的主要途径，而语音是语言的表现形式[1]。语音在一定程度上可影响人们的生活，因此，语音信号的研究对科学领域和人们日常生活具有一定的研究价值和意义。噪声广泛存在于生活，信号在传输过程中不可避免会受到各类噪声的干扰，降低了信号的可读性，因此对携带噪声的信号进行去噪处理十分必要[2-4]。语音信号是一种特殊的信号，其在传输过程中，由于外界环境和设备的影响不可避免会被噪声干扰，一定程度上影响了人们所接收信息的准确性。人们提出了各种语音去噪方法[5，6]，其中，常用的有滤波器去噪法、小波分析去噪法以及小波包分析去噪法[7]。

MATLAB是一种功能强大，具有很好的交互性的数值计算和可视化计算高级语言，其强大的矩阵运算，数值分析以及信号处理功能使其广泛应用于众多科学领域中[8]。因此作者使用MATLAB作为设计工具软件来进行语音信号去噪处理。

作者在MATLAB环境下应用滤波器去噪方法对加噪声的语音信号进行时域、频域的分析和滤波。通过MATLAB编程对语音信号被噪声污染进行仿真处理，并对加噪声前后的频谱图进行对比；然后根据语音信号特点设计各类滤波器；最后将所设计的滤波器分别应用于含噪声的语音信号，并对其频谱图进行对比分析，确定最优化方法。

1 总体设计

利用MATLAB作为平台实现滤波和频谱分析，主要分为语音信号采集、语音信号分析、语音信号加噪、滤波分析以及GUI设计五个模块，系统框图如图1所示。

首先对采集的语音信号进行频谱分析，然后对其进行加噪并对加噪后的信号进行频谱分析。而滤除噪声的方法选择了噪性能较好的滤波器方法，即通过设计有限脉冲相应FIR滤波器以及无限脉冲相应IIR滤波器来完成，并利用这两种方法对加噪后的语音信号进行去噪处理，然后从频域角度对结果进行了对比分析。最后为了加强程序的友好性和可视性，采用GUI编程的方法来设计语音信号去噪系统用户界面。

2 语音信号采集和加噪

2.1 语音信号采集

文章利用PC机声卡对语音信号进行采集。PC机的声卡采样率一般在64 KHz以上，即一秒钟可以采集64 000个声音样本。而人们正常的语音信号一般在300 Hz至34 000 Hz之间，根据奈奎斯特采样定理，一般的正常的语音信号均可以利用声卡采集并且保证其不失真。在安静环境下的正常交流可以近似为纯语音信号，声音信号的长度最好控制在10 s内以便后期分析处理。

图2为通过声卡采集得到的语音信号波形及其频谱。

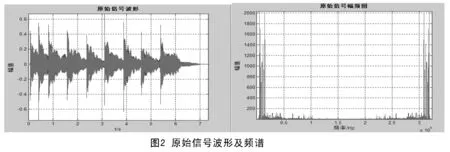
2.2 语音信号加噪

对已经获得的纯语音信号进行加噪处理来模拟在实际生活中语音信号被噪声污染的情况。利用MATLAB中的audioread函数把语音信号转换成序列，得到信号信息；sound函数可以将采样序列通过声卡转换成声音，可直观听出加噪前后的区别。高斯白噪声可用具体的数学表达式表示，且可以贴近反映实际信道中的加性噪声的情况[9]。

文章选择对语音信号加入高斯白噪声来模拟声音被污染的情况。利用MATLAB中的随机函数(rand或randn)产生符合高斯分布序列的噪声序列并将其加到语音信号中，用来模拟语音信号被污染。通过对其频谱分析，声音的回放可以很清楚的听出加噪前后的区别[10]。也可以通过sound函数便可以听到加噪后的语音信号，与原始语音信号相比，声音刺耳根本不能分辨出原始语音信号。

图3为利用MATLAB得到的加噪后的信号波形。

通过频谱结果可以看出，噪声均匀分布在整个频域范围内，但原始信号的主要部分并没有消失，表明进行合适的滤波处理后后很有可能恢复出原始信号，至少可以减弱噪声的影响。与之前的原始信号频谱对比可看出，如将滤波的范围设定在50 kHz 就可能实现滤出噪声的目的。

3 语音信号去噪方法

对于语音去噪现在已经有一些比较成熟的方法，如小波变换法，小波包变换法，以及滤波器法。利用小波的方法去噪设计过程相对繁琐，因此，选用滤波器方法来实现去噪功能[11]。数字滤波器若按照冲激响应来分类可以分为FIR滤波器和IIR滤波器两种。其中FIR为有限脉冲响应滤波器，IIR滤波器是无限脉冲响应滤波器[12，13]。

3.1 IIR滤波器语音去噪

IIR滤波器一般有三种设计方法，分别为：零极点位置累试法、利用模拟滤波器设计数字滤波器和最优化设计法。本文选用滤波器方法，在设计IIR滤波器的时候可以借鉴经典的成熟的模拟滤波器，如巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等[14-16]。 文章将使用巴特沃斯低通滤波器来设计数字滤波器。

由原始语音信号及其加噪前后的频谱分析可知，所设计滤波器应该要实现的功能是滤除掉出语音信号之外的噪声部分的频率，根据要求给出技术指标如下：

低通滤波器的性能指标：fp=1 000 Hz，fs=1 200 Hz，αs=50 db ,αp=1 dB

高通滤波器的性能指标：fp=3 500 Hz，fs=4 000 Hz，αs=50 dB，αp=1 dB

带通滤波器的性能指标：fp1=1 200 Hz，fp2= 3 000 HZ，fs1= 1 000 Hz，fs2=3 200 Hz，αs=100 dB，αp=1 dB

其中fp表示通带截止频率；fs为阻带截止频率；αp表示最大通带衰减；αs表示最小阻带衰减。

当得出相关的技术指标后便可以利用经典滤波器来设计低通滤波器，这里采用巴特沃斯滤波器来设计模拟低通滤波器，并得到低通滤波器的系统函数，即H(s)。得到一个可以实现相关功能的模拟低通滤波器后将会采用频率变换的方法通过低通滤波器的系统函数变换出相关的高通、带通或带阻滤波器的系统函数。

3.2 FIR滤波器语音去噪

与IIR相比，FIR滤波器的优点表现在线性相位以及容易设计两点上。一般来讲对于需要线性相位时考虑FIR滤波器，当对线性相位较低时我们采用IIR滤波器代替[17]。对FIR滤波器的设计一般用窗函数法和频率采样法设计。其中窗函数法是我们设计FIR滤波器长用的方法，用这种方法来设计相应的FIR滤波器。

利用窗函数法设计FIR滤波器的流程图如图4所示：

利用窗函数法设计FIR滤波器一般需要给出理想滤波器的频率响应即Hd(ejω)，由于添加窗函数是在时域用窗函数与所给的信号相乘来达到截断信号的目的，因此需要使用序列傅里叶反变换求得Hd(ejω)的单位脉冲响应hd(n)。由于hd(n)无限长的序列且为非因果，采用加窗函数的方法来让hd(n)转换为有限的因果脉冲序列h(n)，最后通过序列的傅里叶变换，把h(n)变换为H(ejω)[18-19]。

通过上述的步骤可以得出H(ejω)，以后需要把它和预期的滤波器频率响应进行比较。如果符合预期的标准则成功，否则需要再修改窗函数。

4 去噪及仿真实验

4.1 FIR滤波器滤波前后对照

在MATLAB中FIR滤波器滤波使用函数fftfilt，其调用方式分为两种[20]。分别为Y= fftfilt(b，x)：对信号x进行基于FFT和重叠相加法的FIR滤波；以及Y=fftfilt (b,x,n)：参数n用来控制进行FFT变换的点数。

下面将给出利用FIR滤波器进行滤波后频谱图：

利用窗函数法设计的FIR低通滤波器，FIR带通滤波器和FIR高通滤波器滤波前后频谱图如图5所示，

从图5可以看出，波频谱的横坐标表示频率单位为Hz，纵坐标表示信号幅度。而其中的波形图横坐标表示频率单位为Hz，纵坐标表示信噪比单位为dB。从滤波前后的频谱图我们可以看出，原始信号的有效频率范围为50 000 Hz以下，但高通滤波器将有效部分滤出了，而低通和带通滤波器的保留了原始信号的有效部分。

4.2 IIR滤波器滤波前后对照

图6为仿真得到的IIR滤波器滤波前后的频谱对照图，

图6中的波频谱的横坐标表示频率单位为Hz，纵坐标表示信号幅度。而其中的波形图横坐标表示频率单位为Hz，纵坐标表示信噪比单位为dB。

从图中可以看出原始信号的频率范围在50 000 Hz以下，而用IIR滤波器进行滤波，低通和带通的情况都可以保留原信号，但高通滤波器不能用，因为有效的信号被滤除掉了。其中若比较IIR低通和IIR带通滤波器发现，虽然都保留了原始信号，但相对来讲IIR低通滤波器可能效果更好一点。

因此，当可以确定FIR和IIR均可以实现所需要的功能的情况下，FIR滤波器和IIR滤波器针对不同的情况有不同的选择，具体来讲IIR滤波器可以用相对较少的阶数来达到滤波的目的，而且可以根据模拟滤波器原型来设计相对工作量较小。FIR滤波器由于为有限单位脉冲响应因此必为稳定的，而且FIR可以采用FFT算法但IIR滤波器不能这么算，另外FIR滤波器的应用更为简单。

4.3 对含噪声的语音信号去噪

前面用纯语音信号来模拟正常的语音信号，并利用MATLAB来模拟语音信号被污染，测试设计了相应的滤波器。下面对现实生活中的含噪声的语音信号进行去噪分析。

对语音信号的采集确实有很多办法，需要采集两次即正常的安静情况下和比较嘈杂的情况(即含有噪声的情况)。但是如果利用自己的声音来当做声音样本，我们在两次采集的时候不能保证两次说话的语调、音高、响度等等是相同的，即不能保证频谱相同。因此，采集的方法是在网上下载一份纯音乐音频并保存在手机里，分两次播放：在安静的情况下和在人为制造一个嘈杂环境。通过分析对比这两次的频谱和波形来确定适合的滤波器并尝试进行去噪。图7(a)为利用MATLAB得到的波形图和频谱图，图7(b)为采集到的信号加噪声后的波形和频谱图。

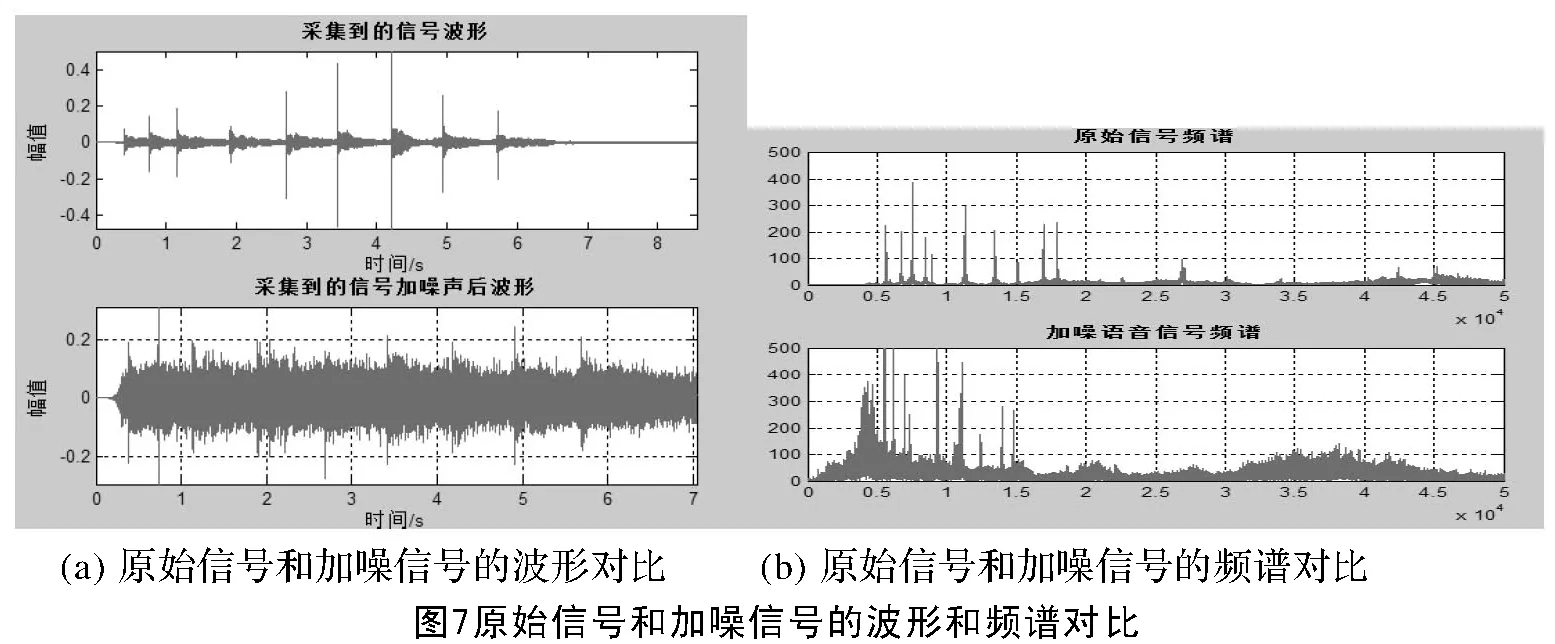
从图中可以看出，噪声的作用范围大概在整个频域内，但是通过原始语音信号的频谱图可以看出语音信号主要在5 kHz～20 kHz之间，因此需要滤除掉其余的部分。

通过前面分析可知，对于利用MATLAB模拟的噪声环境中FIR低通滤波器和IIR低通滤波器的效果最好。而且从频谱图可知采集的语音信号加噪后与利用MATLAB模拟的语音信号加噪后的效果很类似，因此使用FIR低通滤波器和IIR低通滤波器来进行滤波处理。利用MATLAB滤波后的结果如8所示。

同样通过MATLAB中的sound函数可以听到滤波后的声音，通过和之前的加噪声的结果相比可发现，IIR低通滤波器和FIR低通滤波器滤波后的效果虽然没有达到将原信号完美还原，但是对比加噪的信号可以很明显的听出噪声被减弱了很多。而且对比语音信号的波形，虽然不能还原原信号的波形，但经过滤波后已经较为接近原来的信号波形。

5 结论

利用MATLAB中对纯语音信号进行算法加噪模拟仿真，总的来讲低通滤波器可以达到滤波的作用，带通滤波器其次而高通滤波器则无法实现这个功能，经过高通滤波器的信号已经完全丢失了原信号所携带的信息。根据语音信号的特点，一般在研究语音信号的时候不考虑它的相位问题，而且IIR滤波器的设计思路较FIR滤波器来讲较为简单，因此选择两种滤波器的时候建议选择IIR低通滤波器。滤波器对语音信号进行去噪处理应该对语音信号和噪声的频谱进行十分精确的分析，这样才能得出较准确的滤波器参数，也就是说，利用数字滤波器的方法完全可以达到对语音信号去噪或降噪的目的。

[1]林涛.基于MATLAB的有噪声语音信号处理[D].北京：北京大学，2011.

[2]吴岳松.基于听觉模型的水下目标识别研究[D].南京：南京林业大学.

[3]丁兰兰.基于MATLAB的有噪声语音信号处理[D].大连：大连理工大学，2011.

[4]林清川，白羽，索丽敏，等.基于MATLAB的数字图像处理分析及应用[J].黑龙江科技信息，2009(32)：84.

[5]张劲松. 基于MATLAB的语音信号采集和分析系统的可视化设计[J]. 齐齐哈尔大学学报(自然科学版),2006(6)：43-46.

[6]余道衡.数字信号处理的发展与应用[J].科学前沿与技术评论，1999，21(3)：36-39

[7]孙红英 基于CS理论的语音增强算法的研究 [D].兰州：西北师范大学，2011.

[8]周宁宁.基于中介数学系统处理图像的方法研究及其在虚拟环境中的应用[D].南京：东南大学，2008.

[9]孙亚飞.小波分析理论应用于岩石松动圈声波测试的研究[D].武汉：武汉理工大学，2008.

[10]薛年喜.MATLAB 在信号处理中的应用(第二版)[M].北京:清华大学出版社，2005.

[11]吴培希.有关零相数字滤波器的实现[J]. 信息系统工程,2012(11)：95-96.

[12]逯广义.基于Multisim中Filter Wizard的滤波器设计[J].电气转动自动化，2009，31(1)：56-57.

[13]MZTRA S K.数字信号处理期末综合实验报告[M].孙洪泽，译.北京：电子工业出版社，2005.

[14]朱正平.遥感影像的模糊识别[C]∥中国地球物理学会第18届年会.北京:中国物理学会,2002.

[15]李怀洲，丁兆国，徐伯庆，等.基于VC++的数字滤波器的设计 [J].自动化仪表，2004，25(12)：18-20.

[16]余丹，孙文.MATLAB 软件设计应用之 IIR 数字滤波器[J].技术与市场，2015(6)：251-252.

[17]张福玲. 数值分析教学与实验系统的设计[J]. 电脑知识与技术,2007(13)：290-291.

[18]李亚军. 在MATLAB图形用户界面设计中使用ActiveX控件[J]. 计算机与数字工程,2006(12)：135-137.

[19]阴艳丽. 基于MATLAB语音信号处理的研究[J]. 中国新技术新产品,2012(12)：28-29.

[20]赵世明.基于小波分析的语音增强算法研究[D].安徽：安徽理工大学，2012.

(责任编辑：龙海波)

A Matlab-based Speech Signal Denoising Method

HAN Chang-jun

(SchoolofInformationEngineering,EasternLiaoningUniversity,Dandong118003,China)

The noise in speech signal was removed by methods of IIR and FIR in the domain perspective with Matlab. The results of the denoising by the two methods were compared. To improve the friendliness and visuality, a denoising system user interface was designed by GUI program. It was found that this method effective in extracting speech signal with noise.

speech signal; Matlab; filter; denoising; frequency domain

10.14168/j.issn.1673-4939.2017.01.14

2016-09-06

韩长军(1975—)，男，辽宁丹东人，硕士，副教授，研究方向：电子信息技术及网络应用技术。

TN912

A

1673-4939(2017)01-0072-06