求三角函数最值的常见方法

张亚娇

1．山西省实验中学方山高中，山西 方山 033100；2．山西师范大学教育科学研究院，山西 临汾 041000

求三角函数最值的常见方法

张亚娇1，2

1．山西省实验中学方山高中，山西 方山 033100；2．山西师范大学教育科学研究院，山西 临汾 041000

属于基本初等函数的三角函数和其他数学知识有着密切联系且被应用到很多方面，要更好地掌握三角函数的有关知识就需要对求其最值的方法进行归纳。本文通过对典型例题进行分析，归纳总结了一些求三角函数最值的方法和技巧，主要包括直接求解、转化法、数形结合等方法，并对它们的使用方法作了简单的说明。

三角函数；最值；单调性

对三角函数最值的求解是求解函数最值中较为重要的一部分，在历年高考中也多被用作主要考点。本文主要对三角函数最值问题的一些求解方法和技巧进行了系统的归纳总结，并列举一些具有象征性的例题作简要的分析，借以说明其求解的方法和技巧。

一、求三角函数最值的常见方法

(一)利用三角函数的定义及其符号规律求解

分析：解答本题时首先要考虑三角函数值的符号规律，分四个象限。

综上所述，函数f(x)的最大值为4，最小值为-2。

(二)利用三角函数的有界性求解，即利用|sinx|≤1，|cosx|≤1来求解

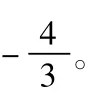
(三)利用函数的单调性求解

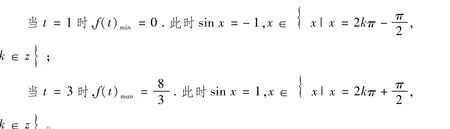
(四)转化为一次函数y=kx+b(c

例4：求函数y=a+bsinx(b≠0)的极值。

分析：由于|sinx|≤1，因此题目其实是要求一次函数y=a+bx1(-1≤x≤1)的条件极值，其中x1=sinx，这里的约束条件是由sinx的值域给出的。

解：1)当b>0时，ymax=a+b，ymin=a-b．

2)当b<0时，ymax=a-b，ymin=a+b．

上面所总结的求三角函数最值的方法只是一些比较常见的方法，可能并不适用于所有的问题。有些题目比较特殊，不能用上述任何方法来求解，而有些题目则可以用好几种方法来求解。在具体的解题过程中，我们要注意具体情况具体对待，选择最简洁最合适的方法来解题。比如下面这道题：

求三角函数最值时需要注意的几个方面：

1．求三角函数最值的方法有配方法、化归法、换元法、基本不等式法、数形结合法等；2．三角函数的最值一般是在一定的范围内取得的，所以解题时一定要注意题目中给定未知数的范围；3．在对函数式进行三角变换和代数换元时要注意函数之间的等价性以及正、余弦函数的有界性；4．题目中含有参数的情况下，要注意考虑参数对求解最值时的作用和影响。

[1]课程教材研究所中学数学教材研究开发中心编．普通高中课程标准实验教科书·数学4(必修)[M]．北京：人民教育出版社，2004．

张亚娇(1990-)，女，汉族，山西方山人，工作单位：山西省实验中学方山高中，读研单位：山西师范大学教育科学研究院，学科教学(数学)专业。

G633．6

A

1006-0049-(2017)02-0169-01