利用弦链系统模拟量子力学中的Dirac梳

刘 尚,姚文杰,荀 坤

(北京大学 物理学院，北京 100871)

利用弦链系统模拟量子力学中的Dirac梳

刘 尚,姚文杰,荀 坤

(北京大学 物理学院，北京 100871)

利用弦链系统模拟Dirac梳，将力学系统中的一维弦链的振动与量子力学一维周期性势场中的电子波函数进行类比，这2个系统具有等价的本征方程，因此其本征谱也应该具有相同的特性，例如具有能带结构. 通过实验测量和数值计算研究了弦链系统的本征谱分布，发现结果有一定偏差，这种偏差可能来源于非零的副弦质量、主弦的弹性以及主弦和副弦之间非零的接触点尺寸，适当修正之后得到了与实验相符的计算结果.

Dirac梳;弦链系统;动力学模拟

Dirac梳在量子力学中是一个非常有名的例子,它说明了电子在周期性的势场中会存在能带结构[1], 这是固体物理当中一个普遍而重要的结论[2]. 不过, 由于势能函数的特殊性, 要从实验上研究电子Dirac梳几乎不可能. 而许多研究已经表明：不同物理系统中的波(如机械波、光波、电子波等)往往具有相似的性质[3-7]，为此尝试将复杂的量子力学问题简化为经典力学中的问题, 从而更方便地理解电子波函数在一维Driac梳中的行为. 贺卓然等人曾借助于对弦质量密度分布具有周期性的弦链系统的振动模测量,间接得到了电子Dirac梳的能谱[8]. 本文进一步建立弦链系统,其满足的本征波动方程与Dirac梳的定态薛定谔方程在数学上完全等价. 测量了该弦链系统的振动谱，并与数值计算结果进行了比较,发现由于实验条件并非理想,实验结果和理想的Dirac梳还是存在一定的差别. 通过分析指出了差别的来源并进一步修正,计算结果与实验结果比较好地吻合.

1 理论基础

1.1 Dirac梳

图1 Dirac梳示意图

Dirac梳是量子力学中描述一维周期性势场非常常用的例子之一,它所描述的势场是δ函数型的一维周期性势场,如图1所示. 其势能函数可写为

V(x)=∑nV0δ(x-na) ,

(1)

其中a为势场的周期. 根据量子力学的Bloch定理,在周期性的势场中波函数一定可以写为Bloch函数的形式:

ψ(x+a)=eiκaφκ(x),

(2)

其中κ为待定的波数. 而定态薛定谔方程为

-22md2dx2+V(x)ψ=Eψ.

(3)

将势场V(x)的表达式(1)代入方程(3),可以看到在x≠na时,方程解可以很简单地表示为

ψ(x)=Aeikx+Be-ikx,

(4)

其中k为波函数的波失,A和B是待定常量. 利用x=na时的衔接条件可以得到波函数所满足的方程为

cos (κa)=cos (ka)+mV0k2sin (ka).

(5)

通过方程(5)可以看到,方程左侧的值只能位于-1和+1之间,而方程右侧的值根据不同的k值,在某些特定的取值下会出现绝对值大于1的情况,此时方程无解,也就是说这些k值不能取,出现所谓的能隙.

上面的讨论是无限的周期性的Dirac梳,然而在现实中只能考察有限的情况,进一步的理论分析表明有限的周期性势场下,能带结构依然存在, 但是每个能带内的能级都是分裂的.

1.2 弦链系统的动力学方程

设主弦线密度为μ,主弦张力为T,弦上某点横向位移为ψ(x),单位弦长受到的横向力为f(x,ψ,t),则弦的动力学方程可以写为

μdx∂2ψ∂t2=T∂2ψ∂x2dx+f(x,ψ,t)dx.

(6)

这是弦链系统普遍适应的方程. 由于所考察的弦链系统意在和Dirac梳进行对比,所施加的单位弦长受到的横向力为周期性δ函数形式的线性回复力:

f(x,ψ,t)=-∑ifδ(x-xi)ψ,

(7)

其中xi=ia(i=1,2,…,n). 将式(7)代入式(6)并通过分离变量简化可以得到:

-d2dx2+∑ifδ(x-xi)ψ=k2ψ,

(8)

其中k=2πf/v为所求振动模的波数,v=T/μ为弦上波速. 可以看到,上述弦的动力学方程(8)和Dirac梳中电子运动的薛定谔方程(3)在形式上是完全一致的,它们唯一的区别在于(3)式中的E可以小于0,而(8)式中的k2不能小于0,因此弦链系统同样存在“能带”结构.

2 实 验

2.1 实验装置

图2为实验装置的简要示意图,通过定滑轮给主弦挂上砝码来产生主弦张力T,挂上砝码后将主弦两端固定作为固定边界条件. 采用镍质的琴弦作为主弦,0.4号钓鱼线作为副弦,与主弦垂直提供等效线性回复力. 副弦的张力通过挂砝码的杠杆提供,可以通过调节砝码挂在杠杆上的位置来调节副弦中的张力.

图2 实验装置示意图

考虑到副弦中张力太大容易被拉断,为此使用了2根钓鱼线作为1根副弦并以如图3的方式搭在主弦上,这样保证了对称性. 最后,实验中弦振动源起振的简谐信号和主弦的响应信号用SR785动态分析仪来分别实现输出和收集:动态分析仪和弦链系统通过起振器和接收器联系起来. 起振器将分析仪输出的电子信号转化为交变磁场,以此驱动铁质的主弦产生振动(需要另外使用永磁体提供偏置磁场，否则主弦的振动信号将只含有二倍频和更高频的信号),而接收器可以记录下主弦在若干个基频周期内的振动信号,然后在分析仪中通过傅里叶变换求得所需频率的振幅. 若使输出频率在一定范围内进行扫描,则可以得到主弦振动关于频率的响应曲线,曲线的峰值处即为所需的本征频率.

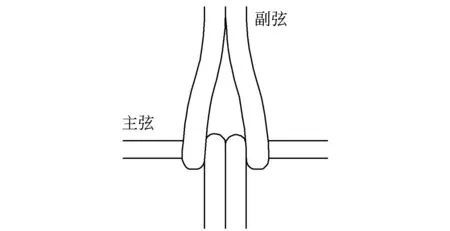
图3 副弦搭载示意图

需要注意的是,装载副弦时考虑到整体的周期性,对于副弦以1根、3根、7根的方式加载,分别将主弦分割成2,4,8等分. 另外,起振器和接收器的位置要避免放在波函数的波节处,否则会出现所谓的“缺级”现象,即本来应该有共振峰处突然间变成波谷. 因此,实验中需要调节起振器和接收器的位置xs和xr,直到所有的峰都能被探测到为止. 另外，实验时起振器上需放小磁铁用以减弱二倍频带来的影响.

2.2 实验结果

实验采用的参量如下:

1)起振器和接收器位置xs=190 mm,xr=1 410 mm.

2)主弦参量:μ=0.696 g/m,T=10.94 N,L=1 800 mm.

3)副弦参量:μf=0.081 8 g/m,F=23.8 N,Lf=157 mm.

其中主弦线密度μ和副弦线密度μf由分析天平测得,主弦张力T和副弦张力F由测力计直接测得,主弦长度L、副弦长度Lf以及起振器和接收器的位置xs和xr由米尺测得.

可以利用Matlab对此弦链系统进行模拟. 将f=2FTLf代入方程(8)可得:

-d2dx2+∑i2FTLfδ(x-xi)ψ=k2ψ,

(9)

其中ψ所满足的边界条件为ψ(0)=ψ(L)=0. 离散化后,方程(9)可方便地数值求解. 在实际计算时,通过比较不同离散化精度下的计算结果来判断所求得的数值解是否在所需精度下收敛.

考察每种实验条件下的前3个能带, 实验结果和理论预期的对照如图4所示, 蓝色实线为实验测得的响应曲线,黑色虚线为理论预测值.

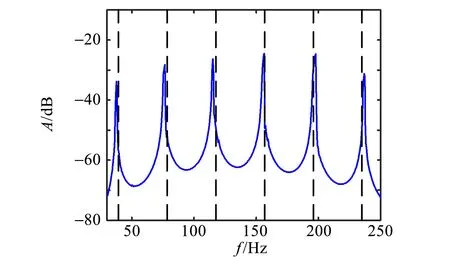
(a)n=0

(b)n=1

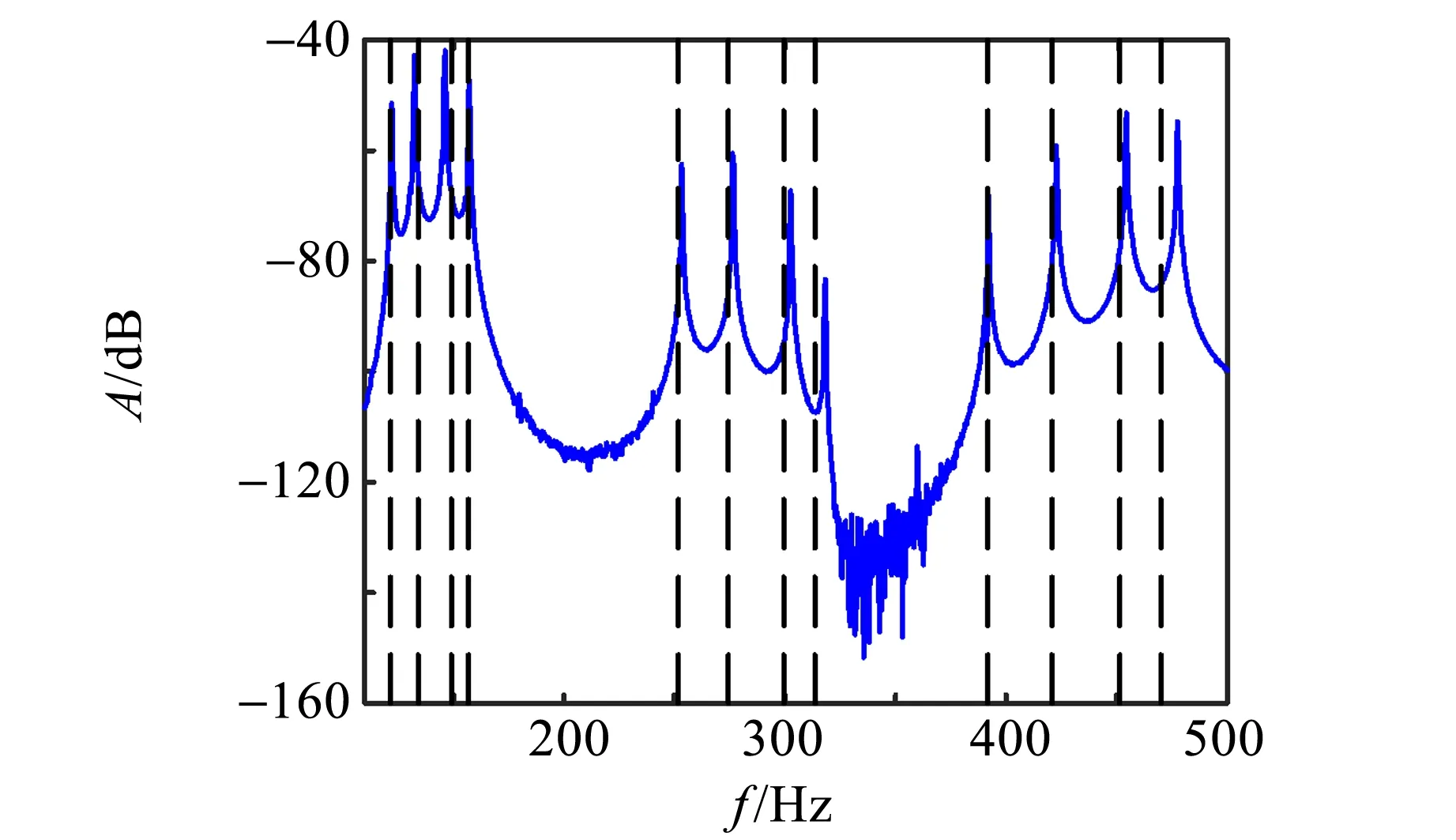
(c)n=3

(d)n=7图4 实验测量响应曲线及理论预测值

从图4(a)可以看到,裸弦(n=0)没有能带结构,理论的本征频率和实验测得的共振峰基本是吻合的,这证明了测量的主弦参量基本上没有问题. 加了1根副弦的情况(n=1)如图4(b)所示,可以比较清晰地看到3个能带,每个能带内有2个峰值,这与理论预期相符. 加了3根副弦的情况(n=3)如图4(c) 所示,同样是3个能带,此时每个能带内有4个峰,理论预测值和实验测得的共振峰有一定的偏差. 加了7根副弦的情况(n=7)如图4(d)所示,能带结构依旧比较明显,此时每个能带内有7个峰,理论预测值和实验测得的共振峰偏差已经非常大了,说明理论模型存在问题,需要进行修正.

2.3 理论修正

为了分析偏差的来源,一方面,考虑到副弦有质量,副弦的振动肯定会对主弦的振动带来一定的影响;另一方面,图4(d)中每个能带的最后共振峰和理论值相差较多,而从理论上讲,每个能带的最后峰应该是副弦所处的位置，正好是波函数的节点处,也就是说副弦不会对主弦的振动带来影响, 因此对于主弦本身也需要进行修正.

根据上述分析,首先对主弦进行修正. 由于图4(a)只测量了前6个本征频率,而图4(d)中出现了24个频率,首先对裸线的24个本征频率进行测量,测量结果如图5(a) 所示. 可以看到,本征频率随着序号的增加基本呈线性增加,如果对于每个本征频率处做相对偏差绘图Δf=fexp-ftheory,如图5(b)所示,可以看到实验值随着序号增加总体比理论值进一步偏高.

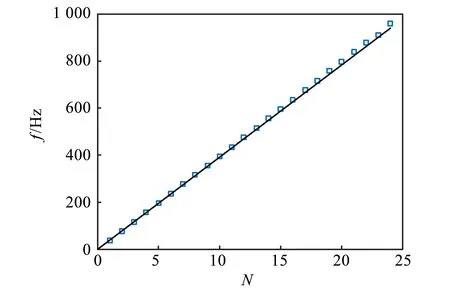
(a)实验测得的本征频率

(b)实验测得的本征频率和理论值之差图5 裸弦的本征频率

表1 主弦等效线密度μeff

接下来对副弦进入修正. 在理想情况的方程中,2Fψ/Lf是主弦在节点处受到副弦施加的作用力,它假设副弦在主弦一侧的形态总是1条直线,现在应当改成某个未知的参量Ii,其中下标i用于表示不同的节点. 再考虑到副弦的振动方程,结合牛顿第三定律,得到系统的振动方程组:

-d2dx2ψ+1T∑iIiδ(x-xi)=ω2v2ψ,

(10a)

(10b)

其中yi和ui(yi)分别为第i根副弦的坐标和振动横向位移,vf为副弦波速. 取副弦坐标范围为yi∈[-Lf,Lf], 则yi=0处为主弦和副弦的相交节点. 显然我们只关心满足ui(y)=ui(-y)的对称解,所以可以把求解范围缩减一半. 对(10b)式在yi∈[-ε,ε]的范围内积分,并取ε→0的极限,可以得到:

-2duidyi0+-1FIi=0,

(11)

则

Ii=-2Fduidyi0+.

(12)

这样解出了节点耦合力的显式表达式,这和直接对节点处进行受力分析得到的结果一致. 最终得到可以离散化求解的方程组:

-d2dx2ψ(x)+1T∑iIiδ(x-xi)=ω2v2ψ(x),

ψ(0)=ψ(L)=0,

ui(0)=ψ(xi),ui(Lf)=0.

(13)

(a)n=0

(b)n=1

(c)n=3

(d)n=7图6 修正后的理论值和实验值比较

在考虑了对主弦和副弦的理论修正以后,修正后的理论预测值和实验结果的比较如图6所示,修正后的理论预测值用红色的虚线表示，蓝色实线为实验结果. 可以看到,对于n=0的情况,修正前后的理论值一致,如图6(a)所示;对n=1的情况,修正前后的差别不大,都和实验结果符合得较好,如图6(b)所示;对n=3的情况,修正后的结果比原来更接近实验结果,如图6(c)所示;对n=7的情况,在不修正时理论预测值和实验结果有很大偏差,修正后可以基本吻合,见图6(d).

总之,由于副弦质量带来的影响,把原来的1个能带内带宽给拉大了,这样的结果是不同能带间的能隙变小了,这对于观察能带结构不利. 为了实验中清楚地看到能带结构,可以采取减小主弦张力或者增大副弦张力的办法,但是这样做可能会引入主弦被副弦扭曲的形变,在具体操作时需要折中考虑.

3 结束语

本实验通过弦链系统成功地模拟了Dirac梳,观察到了能带结构,并对n=1,3,7的3种情况做了比较详细的探讨. 同时,对一般的弦动力学方程的理论进行了主弦和副弦的修正, 通过修正后的理论与实验结果吻合得较好.

致谢：感谢隋靖扬与我们分享在此实验上得到的结果和经验.

[1] Griffiths D J. Introduction to quantum mechanics [M]. Second edition. Upper Saddle River: Printice Hall, 1995:224-229.

[2] 黄昆,韩汝琦. 固体物理学[M]. 北京:高等教育出版社,2010:153-235.

[3] Maynard J D. Acoustical analogs of condensed-matter problem [J]. Rev. Mod. Phys., 2001,73(2):401-417.

[4] Lindsay R B. Elastic wave analogies to the motion of electrons in force fields [J]. Proc. Nat. Acad．Sci., 1934,20(3):177-179.

[5] Khondker A N, Khan M R, Anwar A F M. Transmission line analogy of resonance tunneling phenomena: the generalized impedance concept [J]. J. App1. Phys., 1988,63(10):5191-5195.

[6] van Tiggelen B A, Kogan E. Analogies between light and electrons: density of states and Friedel’s identity [J]. Phys. Rev. A, 1994,49(2):708-713.

[7] Openov L A. On the analogy between the classical wave optics and the quantum wave phenomena [J]. Solid State Comm., 2005,133(8):549-552.

[8] 贺卓然,周廷弢,荀坤. 用力学方法测量一维有限狄拉克梳的电子态[J]. 物理实验,2013,33(1):1-3,7.

[责任编辑：任德香]

Simulating the Dirac comb with a string chain system

LIU Shang, YAO Wen-jie, XUN Kun

(School of Physics, Peking University, Beijing 100871, China)

The Dirac comb was simulated using a string chain system. The classical mechanical vibration of this one-dimensional string chain and the electron wave function in a one-dimensional periodic potential had equivalent eigenvalue equations and their eigen-spectra should share the same properties, such as the existence of band structure. The eigen-spectrum distribution of the string chain system was studied by experiment as well as numerical computation, and the results from those two methods did not coincide with each other. Such discrepancy might come from the nonzero mass of the associated strings, the elasticity of the main string and the non-vanishing area of the touching points between the main string and associated strings. By introducing suitable corrections, numerical results finally recovered the experimental ones.

Dirac comb; string chain system; dynamical simulation

2016-05-30；修改日期：2016-09-10

刘 尚(1994-),男,河北石家庄人,北京大学物理学院2012级本科生.

指导教师：荀 坤(1961-),男,贵州兴义人,北京大学物理学院副教授,博士,研究方向为磁性薄膜.

O413,1;O32

A

1005-4642(2017)01-0007-06

“第9届全国高等学校物理实验教学研讨会”论文