预习背景下的数学课堂如何演绎

陈燕虹

预习，是学生自主学习的一种重要途径。有效的预习能为课堂教学奠定良好的知识基础与认知基础。学生间存在着个体差异，预习后的课堂面临的学习差异可能更大。预习后的学生不再是一张白纸，而是怀揣着疑惑、问题和期待进入课堂。那么，如何利用学生的预习成果，把握教学起点，引导学生更深入地参与课堂的探究活动，预习后的课堂如何演绎，这对教师的课堂把控能力提出了更高的要求。

一、“放权”给学生，把握认识的起点，当个倾听者

美国心理学家奥苏伯尔说过：“影响学习的唯一最重要的因素是学生已经知道了什么，要探明这一点，并应据此进行教学。”可见，要放权给学生，每个学生或多或少都了解了一些知识，有了自主探索、独立思考的体验与感悟，学习起点明显高于原生态的学习起点，此时老师就作为倾听者。

教學时教师尽可能少说，让学生汇报自己预习后的收获，做个倾听者，你会深切感受到原来学生的潜力如此之大。学生经历了从解读教材到超越教材的心路历程，解读不仅重在理解，而且也提高了探究的起点。

二、激发求知欲，深入探究，当个促进者

苏霍姆林斯基曾说过：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是个发现者、研究者、探究者，而在儿童的精神世界中这种需要则特别强烈。”学生期望自己获得成功，期望感到自己智慧的力量，体验到创造的快乐。因此，教师应充分利用学生的这一心理品质，激发学生提出自己的疑惑，进行深入的探究，让学生在这个过程中获得成功的体验、情感的满足和经验的积累。在教学《长方体体积计算》这节课时，从反馈结果看，学生知道长方体体积=长×宽×高，也能用这个公式进行体积的计算。但我总觉得学生对这个公式似乎知其然，不知其所以然。但学生又好像满足于现状，缺乏继续探究的热情。怎么办呢？我抓住时机追问：“为什么长方体的体积等于长乘宽乘高呢？”看到同学们一脸茫然，我说：“看来我们对长方体体积的学习还不太全面，还有些问题。所以对于学习老师想送给大家一句名言。”课件出示“学贵有疑，小疑则小进，大疑则大进。——陈宪章”。一石激起千层浪，学生又纷纷陷入了深深的思考。

三、动态生成，展示亮点，当个欣赏者

叶澜教授说过：“课堂应是向未知方向挺进的旅行，随时都有可能发现意外的通道和美丽的图景，而不是一切都必须遵循固定线路而没有激情的行程。”教学中，我尽量让每位学生都能展示探索的成果，让更多学生品尝成功的快乐。学生的思维随时随地都迸出智慧的火花。

四、与反思一路同行

“学而不思则罔，思而不学则贻”，如果学生在经历数学活动后缺少应有的反思，那数学活动的有效性将大打折扣。反思是学生自我教育的重要途径，通过反思能够促进理解，发展思维能力，深入认识数学对象的本质。

比如，右图的《组合图形的面积》，同学们呈现了10种方法，从课堂动态生成的教学资源中提炼出有价值的问题，引领学生反思，追求在解法合理的基础上进一步优化。比如，提出下面的问题引导学生深入思考：

⑴对比图1与图2的两种解法，哪种解法更优越？为什么？

⑵对比图7与图1的两种解法，哪种解法更优越？为什么？

问题⑴中，图1把图形分成两个长方形，图2把图形分割成两个梯形，虽然长方形与梯形都是已学过的图形，但求长方形面积的计算步骤比梯形少。根据图1计算面积是三步运算，根据图2则有七步运算。计算步骤越多，算错的机率越大；如果是近似数的计算，计算步骤越多，误差也会越大。因此，图1的解法显然比图2优越。

问题⑵中，图7把图1中分割成的两个长方形合并成一个长方形。根据图7计算面积只有两步，即（7+4）×3。因此，图7的解法比图1更好。

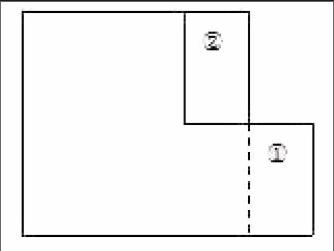
通过上述两个问题的讨论，也许能帮助学生形成正确的数学观念：求组合图形面积，不但要把图形转化成已学过的图形，而且转化成的基本图形的个数要尽可能少，计算图形面积的步骤也要尽可能少。有了如此追求，学生的思维可以得到更大的挑战，也许还能想出这样的解法，割下图形中小长方形①，补到②的位置，拼成一个6×5.5的长方形。

如此反思学生将获益良多，绝不是反复练习所能企及的。因为从探究到反思，思维所经历的是一个从开放到收敛，从无序到有序，从求异到求同，从下意识到有意识的自然进化、发展与提升的过程。反思是重要的思维活动，它是思维活动的核心和动力（弗赖登塔尔）。

预习后的课堂，需要教师在充分了解学生的认知起点的基础上，针对不同层面学生的不同预习程度，灵活选择教学策略，引导学生积极主动探究，让学生的既有认知不断衍生新的认知，并且不断地反思，学生的自主学习能力得到发展、情感得以体验，实现教学效益最大化。