基于mems九轴传感器的智能自主飞行器

2017-02-17华南理工大学电子与信息学院侯昶宇刘彦超周泽群吴克乾

电子世界 2017年2期

关键词：姿态控制陀螺仪加速度计

华南理工大学电子与信息学院侯昶宇刘彦超周泽群吴克乾

基于mems九轴传感器的智能自主飞行器

华南理工大学电子与信息学院侯昶宇刘彦超周泽群吴克乾

本文通过对飞行器常用算法的大量研究，提出了改进后的四元数算法，可以通过系统状态量和加速度计测量值对系统状态进行验证，从而得到该系统的最优状态量，并能实时更新参数矩阵。并在加速度计侦测到各种有害加速度的时候，使姿态监测更加准确。

陀螺仪；姿态控制；卡尔曼滤波，四元数算法

1.引言

飞行器目前在工业、农业、军事上都得到了广泛的应用，地址探测、灾害监测、气象探测的研究等等，飞行器也迎来了大发展的时期。飞行器的飞行状态等相关因素也成为了研究的重点。

目前多数无人机都是采用数据积分并融合的方式进行姿态控制，本文所探讨的是另外一种姿态控制模式即四元数控制算法。通过这种算法来改善飞行状况进行稳定的飞行。

2.项目说明

本项目试图通过改变飞行控制算法来改善飞行器的飞行状况，即：每个采样周期通过读取陀螺仪，加速度计和电子罗盘的数据进行迭代计算，实现四元数随着时间进行更新，进而求得三个姿态角（俯仰，滚转，偏航）。由处理器处理姿态角变化并将指令发送给电子调速器进而控制无刷电机实现飞行控制。项目研究内容：

（1）陀螺仪数据采集；

（2）处理器分析数据；

（3）四元数姿态解算；

（4）飞行控制算法。

3.四元数算法说明

3.1 基本原理

由于载体的姿态方位角速率较大，所以针对姿态矩阵的实时计算提出了更高的要求。通常假定捷联系统“数学平台”模拟地理坐标系，即导航坐标系;而确定载体的姿态矩阵即为研究载体坐标系和导航坐标系的空间转动关系，一般用载体坐标系相对导航坐标系的三次转动角确定。

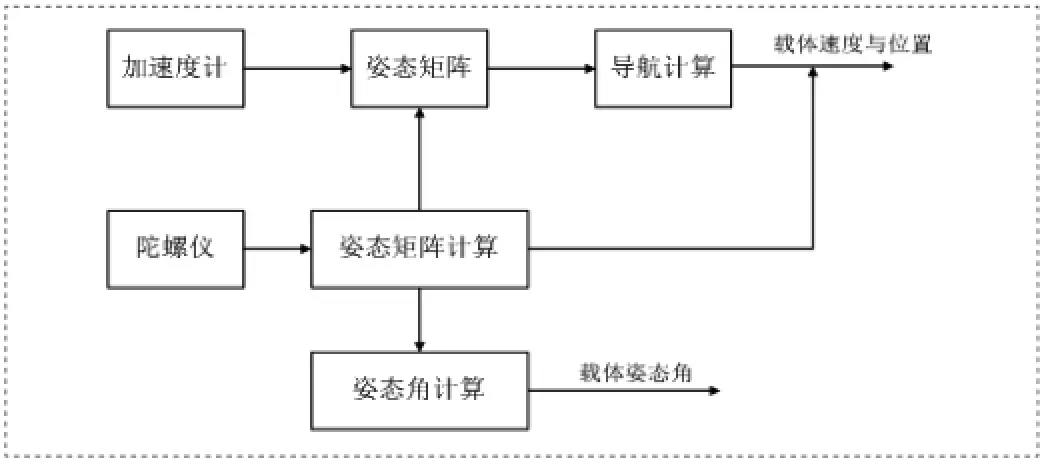
图1 基本原理图

3.2 四元数姿态解算

四元数的数学概念是1843年由哈密顿首先提出的，它是代数学中的内容之一。随着捷联式惯性导航技术的发展，为了更简便地描述刚体的角运动，采用了四元数这个数学工具，用它来弥补通常描述刚体角运动的3个欧拉角参数在设计控制系统时的不足。

图二四元数原理图

一个动坐标系相对参考坐标系的方位可以完全由动坐标系依次绕3个不同的轴转动的3个角度来确定。如把载体坐标系作为动坐标系，把导航坐标系作为参考坐标系，则姿态角即为一组欧拉角，按一定的转动顺序得到导航坐标系到载体坐标系的关系。

上述方法就是通过欧拉角设计飞行控制算法。

图三欧拉角微分方程

通过上面的欧拉角微分方程，可以求得三个姿态角，但由于只有三个方程而且每个方程都含有三角函数运算所以这种算法可能出现奇点，导致向量方向不确定从而不能全姿态工作。

四元数可以描述一个坐标系或一个矢量相对某一个坐标系的旋转，四元数的标量部分表示了转角的一半余弦值，而其矢量部分则表示瞬时转轴的方向、瞬时转动轴与参考坐标系轴间的方向余弦值。

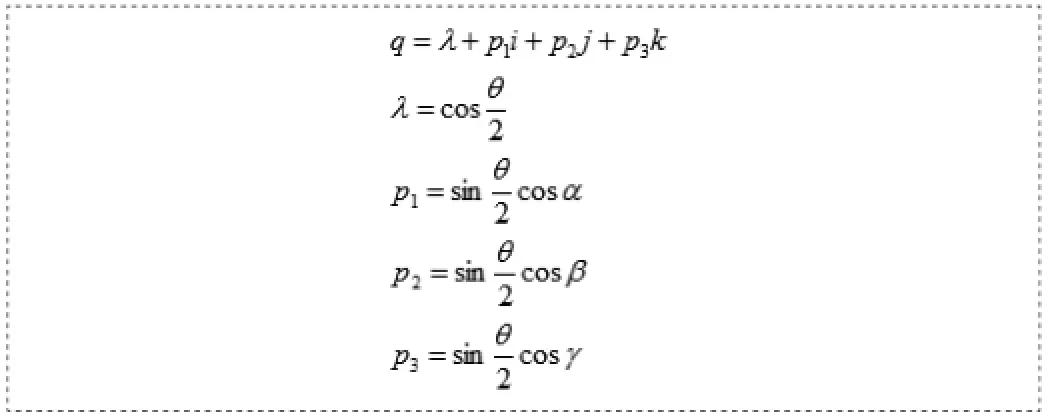
图四四元数算法

四元数算法只用解算四个一阶微分方程式，因此还满足了飞行控制算法中实时性的要求。

3.3 目前常用算法解析

目前多数飞行器使用的是由德国首创的四周控制算法，其算法并没有使用通常意义上的四元数算法，而是采用了一种独特的积分算法。

3．3．1 姿态监测算法

首先，将陀螺仪和加速度计的测量值减常值误差，得到角速度和加速度，并对角速度进行积分，然后对陀螺仪积分和加速度计的数值进行融合。融合分为两部分，实时融合和长期融合。实时融合每一次算法周期都要执行，而长期融合设256个检测周期执行一次。

实时融合：

（1）将陀螺仪积分和加表滤波后的值做差;

（2）按照情况对差值进行衰减，并作限幅处理;

（3）将衰减值加入到角度中。

长期融合：

长期融合主要包括两个部分，一是对角速度的漂移进行估计(估计值是要在每一个控制周期都耦合到角度中的)，二是对陀螺仪的常值误差(也就是陀螺仪中立点)进行实时的修正。

（1）将陀螺仪积分的积分和加速度积分做差，这里之所以要使用加表积分和陀螺仪积分的积分，是因为在256个检测周期内，有一些加速度计的值含有有害的加速度分量，如果只使用一个时刻的加表值对陀螺仪漂移进行估计，显然估计值不会准确，使用多个周期的值进行叠加后平均处理，可以减小随机的有害加速度对估计陀螺仪漂移过程中所产生的影响。

（2）将上面两个值进行衰减，得到估计的陀螺仪漂移

（3）对使考虑了陀螺仪漂移和不考虑陀螺仪漂移得到的角度做差，如果这两个值较大，说明陀螺仪在前段时间内测到的角速率不够准确，需要对差值误差(也就是陀螺仪中立点)进行修正，修正幅度和差值有关

这种姿态监测方法并不是四元数算法，而且计算量也不比四元数算法小。但是编程是更加直观，易于理解，而且参数的调节也会更加方便。这种方法是在尝试着对四元数算法这一复杂相互耦合的多状态变量的线性系统状态估计过程进行了简单的解耦，从而将姿态的最优估计和陀螺仪漂移的最优估计分隔开，这样，就可以通过比较直观的观测手段对两个部分的参数进行调整。而且避开了高难度的卡尔曼滤波设计，因此在设计性上也会更加的合理和易于实现。

3．3．2 姿态控制算法

控制算法的核心是对角速度做PI计算，P的作用是使四轴能够产生对于外界干扰的抵抗力矩，I的作用是让四轴产生一个与角度成正比的抵抗力。

图五控制算法 PI计算

对角速度做I积分运算实际得到的就是角度，如果四轴有一个倾斜角度，那么四轴就会自己进行调整，直到四轴的倾角为零，它所产生的抵抗力是与角度成正比的，但是，如果只有I的作用，会使四轴迅速产生振荡，因此，必须将P和I结合起来一起使用，是四轴非常快速的产生抵抗力矩。

3.4 算法比较与创新

目前常用算法对于系统模型的准确性、模型参数的标定和系统参数的选取的准确性没有很高的要求，而且修改参数时不需要对系统中的很多地方进行大量改变，不需要进行长时间调试。而通过我们改进的算法可以通过系统状态量和加速度计测量值对系统状态进行验证，从而得到该系统的最优状态量，并能实时更新参数矩阵。并在加速度计侦测到各种有害加速度的时候，使姿态监测更加准确。但我们的算法需要大量的实践数据，只通过上位机观测很难得到合适的方法。

3.5 项目成果展示

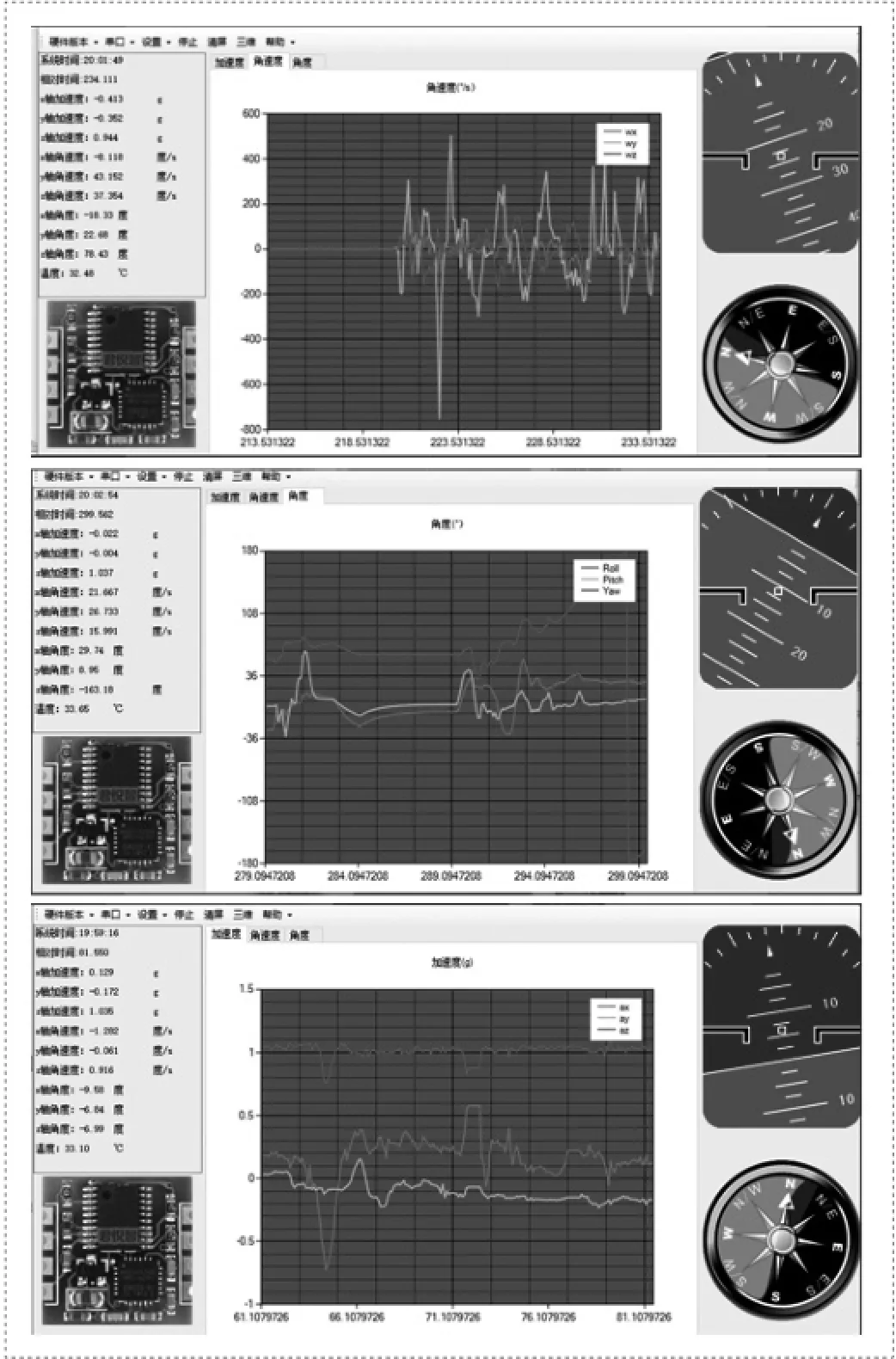
图六传感器数据采集图

图七飞行器静态展示

4.总结

随着技术的发展，飞行器也不再“神秘”，但对于飞行姿态检测的准确性，飞行状态的稳定性，灵活性提出了更高的要求，本文对四元数控制算法与飞行器飞行状态之间的研究，通过一系列真实的飞行实验，从第一阶段的飞行器的姿势检测，到第二阶段的姿势控制，采用PI算法，通过STM32F103输出数据给电子调速器，通过改变无刷电机电流，快速生成合理力矩，使飞行器维持稳定并改变姿态飞行（见图七）。

[1]朱华,刘卫东,赵淳生．变体飞行器及其变形驱动技术[J]．机械制造与自动化,2010,02:8-14+125．

[2]史建国,高晓光．飞行器突发威胁下的智能自主航路规划技术[J]．火力与指挥控制,2010,03:39-41+45．

[3]牛轶峰,沈林成,龙涛．攻击型无人飞行器自主控制技术研究综述[J]．系统工程与电子技术,2007,03:391-395．

[4]刘峰等．四轴飞行器姿态控制系统设计[J]．计算机测量与控制,2011,19(3)．

[5]王东来等．小型四轴飞行器动力学参数测定方法设计[J]．科技导报,2011,29(36)．

[6]邓矛．关于四轴飞行器的姿态动力学建模[J]．科技创新导报,2012(9)．

[7]王萍．驻伊美军装备无人机[J]．轻兵器,2003(11)．

[8]冯琦．军用无人机发展趋势[J]．电光与控制,2003(02)．

[9]S Bouabdallah．Design and Control of quadrotors with application to autonomous flying．Epfl:2007．

[10]常敏,崔永进,何蓓薇,等．四轴飞行器姿态控制系统设计[J]．通信电源技术,2015(5):144-147．

[11]刘峰,吕强,王国胜,等．四轴飞行器姿态控制系统设计[J]．计算机测量与控制,2011,19(3):583-585．

[12]孙娇．关于四轴飞行器姿态控制系统设计与问题分析[J]．工程技术:文摘版,2016(3):00225-00225．