舰船非线性设计值的水弹性直接计算方法

陈占阳,桂洪斌,任慧龙

(1. 哈尔滨工业大学(威海) 船舶与海洋工程学院,山东 威海 264209；2.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

舰船非线性设计值的水弹性直接计算方法

陈占阳1,桂洪斌1,任慧龙2

(1. 哈尔滨工业大学(威海) 船舶与海洋工程学院,山东 威海 264209；2.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

目前各国军规对水面舰船设计载荷的计算还只停留在刚体理论，但随着舰船主尺度的日益增大，船体弹性效应对载荷响应的影响已越发不容忽视，通过水弹性理论计算和试验两方面，与国内规范的设计载荷计算方法进行了比较分析，发现国内规范中对于极限工况下的砰击载荷的贡献考虑不够充分，为此，基于三维非线性时域水弹性理论，对不规则波中船体载荷响应预报方法进行了阐述，提出了一种非线性设计载荷的直接计算方法。基于直接计算方法，提出一套新的水面舰船设计值计算流程算法。通过比较后发现，采用本文修改后的规范算法得到的设计值，与直接计算方法结果更为接近。新的设计载荷计算程序的有效性和准确性得到了证实。

水弹性；非线性；长期预报；设计值；直接计算方法

水面舰船作为海军武器装备不可或缺的一部分，在海军力量上发挥着重要的作用，同时也影响着各国海军军事力量。因此，水面舰船的结构强度能否在今后的军事活动中满足战略要求一直是舰船设计人员最为关注的要点。而作为结构强度校核的重要前提，水面舰船的设计载荷的计算就显得至关重要。目前各国规范中，水面舰船设计值的计算都是基于经验公式，根据船体主尺度确定公式中的待定参数。这种方法虽然简便、直接，但却无法考虑船体型线对载荷响应的影响，英国劳氏军规[1]指出，应采用不规则波长期预报的方法对水面舰船的设计载荷进行计算。此外，随着各类水面舰船的主尺度日趋增大，弹性效应也越加明显。而目前各国军规的设计载荷的计算都还只是局限于刚体理论，仅从经验公式上无法体现出船体的弹性效应对设计载荷的影响，因此急需一种能够计及船体的弹性效应的设计值的直接计算方法。

若要进行不规则波中载荷的长期统计分布，就需要先对不规则海浪中的载荷响应进行时历预报，但目前还采用的是主峰频率法[2]，忽略了不规则波中频率和波幅对载荷响应的影响，这也给计算结果带来一定的误差。由于水面舰船所具有的航速高，外张明显、刚度小等特点，当这类高速水面舰船在高海情下遭遇砰击现象时，载荷呈现极强的非线性特征，为此，本文将时域延迟函数与三维非线性时域水弹性理论相结合，提出一种能够计及砰击的不规则波中载荷响应的预报方法，并基于该法提出一种能够计及船体的弹性效应非线性设计载荷直接计算方法。通过与规范值进行比较分析后，对国内现行军规的不足提出修改建议，最后结合直接计算方法提出一套新的水面舰船设计值计算流程。

1 不规则波水弹性理论计算方法介绍

要进行不规则波中载荷的统计分布，就要先对不规则波中的载荷响应进行时历模拟。以往相关学者大多是针对规则波中的水弹性方法进行研究[3-8]。在时域内，不规则波船体运动的非线性水弹性力学方程可以写作如下形式：

(1)

(2)

式中：B(ω)为频率为ω的广义流体阻尼矩阵。

对于时域延迟函数的求解，邹明松等[9]由于受到网格尺度、数量和波频等数值方法上的限制，时域延迟函数的实际求解过程中，仅可利用有限个频率下的水动力系数，无法准确得到高频下的系数，但若求解高频系数，则会导致数值计算量过大，对硬件条件需求过高的问题，二者很难兼得。为此，本文采用计算高频振荡积分的折线法逼近B(ω)，并采用一种半解析法对B(ω)进行截断处理，并考虑截断误差的影响，同时将其与水弹性理论相结合，进而求得计及船体弹性效应的时域延迟函数。

(3)

式中：α和β都是待定系数，为确保B(ω)是衰减的，β必须保证大于0，则

(4)

至此，就可得到系统的时域延迟函数的无穷限积分Krk(τ)[10]。

对于不规则波而言，为解决以往按照某单一频率的方式求解流体载荷这一弊端，本文将时域入射波力和绕射波力表示成与脉冲响应函数的之间的卷积关系：

(5)

其中

(6)

本文对于砰击力的计算是基于“动量砰击理论”得到单位时间及船长下砰击作用力Fslam(x,t)后沿船表面积分，就可获得计入振动模态分析方程的砰击载荷表达式：

(7)

式中：wr(x)为第r阶模态产生的垂向位移。

对于运动方程(1)的求解，本文采用四阶龙格-库塔(Runge-Kutta)法，该法为显式单步法，具有4阶精度。在得到主坐标后，利用模态叠加原理，得到时域内船体上任意横剖面的位移w(x,t)、弯矩M(x,t)、剪切力V(x,t)。

本文作者曾对某大型水面舰船(以下简称目标船)分段船模试验[11]，图1为航速30 kn，有义波高6 m，特征周期10.877 s目标船的船舯弯矩(VBM)时历与结果比较。

图1 船舯弯矩计算结果和试验结果的比较Fig.1 Comparison between theoretical results and experimental midship bending moments

2 不规则海况非线性设计载荷的直接计算方法

从图1可以看出，剖面弯矩计算结果呈明显的非线性现象，中拱和中垂的波浪载荷分量不相同。由于非线性波浪载荷属于非平稳随机过程，因此针对线性载荷的谱分析方法已不再适用，此时的载荷预报，应采用时域分析和数理统计的方法。

2.1 非线性波浪载荷短期预报

所谓时域分析和数理统计的方法，就是需要将中拱和中垂的时历载荷分量区分开来，即从一开始便采用非线性波浪载荷理论，在时域内算得非线性波浪载荷响应后，对一个足够长的时间历程进行取样，分别按中拱和中垂分量统计样本，如图2，再整理出相应的直方图，然后进行拟合，得到长期分布的概率密度和分布函数，进而得到中拱和中垂的设计值。

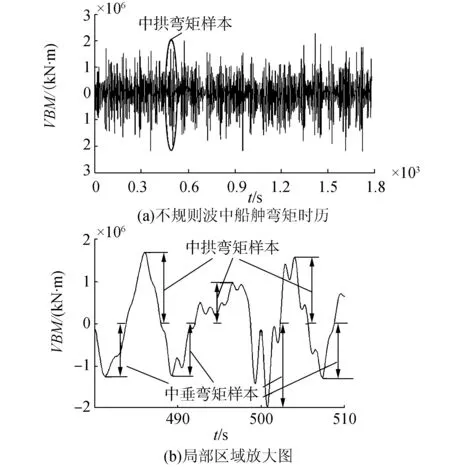
图2 不规则波弯矩幅值样本提取示意图Fig.2 Sketch map of amplitude of bending moment in irregular wave

本文采用Weibull分布进行拟合。取X为非线性波浪弯矩的幅值，则Weibull分布的概率密度和分布函数为

(8)

式中：β为形状参数，η为尺度参数。

本文采用的海况数据是北大西洋海况，借助海况信息对目标船采用Weibull分布拟合，采取一个小时进行短期分布计算。其中，图3～4分别是目标船在某一工况(有义波高H1/3=11.5 m，特征周期TZ=16.4 s)中拱、中垂状态下的合成弯矩和砰击弯矩直方图及拟合曲线。

图3 中拱合成弯矩直方图Fig.3 The histogram of hogging moment

图4 中垂砰击弯矩直方图Fig.4 The histogram of sagging moment

2.2 非线性波浪载荷长期预报

(9)

(10)

然后再通过下式，得到设计最大值

(11)

3 算例比较分析

目标船模型主尺度如表1。

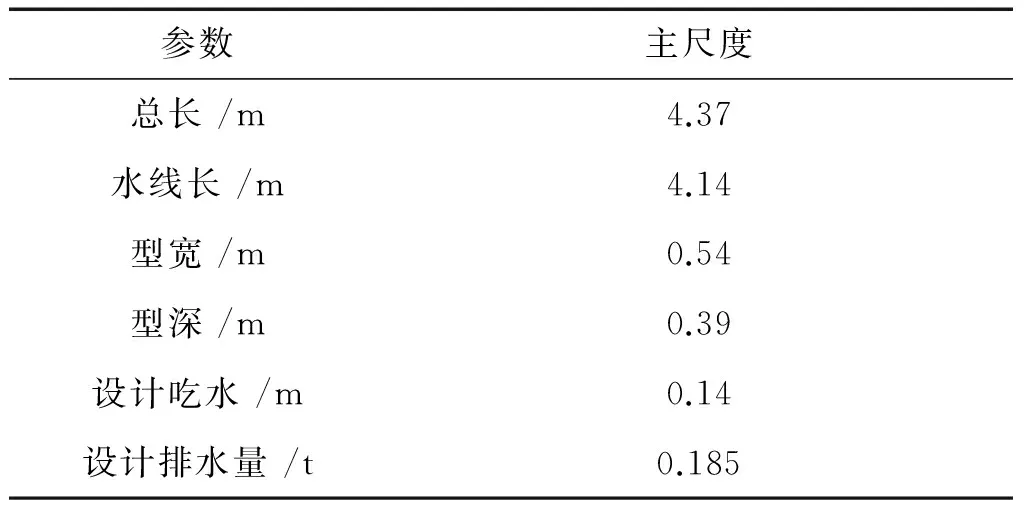
表1 目标船模型主尺度参数

工况介绍如表2。试验分别对准则中巡航、极限工况下的船舯弯矩进行测量，将试验结果与直接计算结果、准则[12]结果进行比较，见表3～4，准则确定的巡航，极限计算。

表2 准则确定的巡航、极限计算工况

表3 巡航工况 (对应n=105)的设计载荷的比较

Table 3 The comparison of design moment cruise sea state (forn=105)

MN·m

表4 极限工况(对应n=108) 的设计载荷的比较

Table 4 The comparison of design moment ultimate sea state (forn=108)

MN·m

此外通过上述比较，还可以发现：

1)利用直接计算方法得到的合成弯矩在计及各项非线性以及船体由于弹性变形后产生的高频载荷成分后，巡航工况中直接计算结果与准则结果、试验结果较为接近，而极限工况由于海况高，非线性因素影响更为剧烈，因此直接计算结果要比规范中的公式得到的结果要偏大，但量级相当，在合理范围内；

2) 对于极限工况而言，波浪弯矩的准则结果偏大，而砰击弯矩的准则结果偏小。准则认为极限工况中砰击弯矩与波浪弯矩比例为20%，然而直接计算结果的比例中拱为49.90%，中垂为64.88%，试验结果的分别是42.16%和68.66%，均大于准则规定的比例；

3) 表4中准则规定的航速是22.5 kn，而直接计算方法是基于北大西洋海况长期分布得到结果，以航速出现的概率P(V)进行衡量。试验用的是5 kn，因为试验过程中，在波高为23.95 m的时候，由于波高太大，螺旋桨发生出水现象，试验航速只能达到5 kn。无论是模型试验还是实船航行时在如此高海况下达到该航速都是极其危险的。

4 规范修改建议及计算流程

通过将水弹性理论与分段模型试验结果相结合，对现行军规进行比较后发现，现行准则中对于砰击要考虑不够充分，由于忽略了砰击的贡献(尤其是极限工况下)，导致最终的合成弯矩差别也很大。针对设计值计算方法上的不足，本文提出一套针对大型水面舰船设计值新的计算流程。

通过上面的比较，本文认为巡航工况的计算方法可仍沿用准则以往的方法，这里重点介绍极限工况的计算流程。

4.1 波浪弯矩设计值的计算

1)计算航速

通过比较发现，对于极限工况，由于5 kn的试验结果与22.5 kn的准则结果十分接近，且由于海况很高，无论是模型试验还是实船航行过程中，出于安全因素考虑，航速都不宜过高，本文通过理论计算和试验研究后，建议极限工况下计算航速应取5～10 kn。

2)计算波长

计算波长仍由下式确定：

(12)

3)计算波高

借助本文提出的直接计算方法结果，重新对极限工况下的波浪弯矩的计算波高h1进行确定，中垂波浪弯矩及中拱波浪弯矩计算波高按如下方法确定：计算航速取5 kn，现计算规则波中非线性合成弯矩随波高的变化,并绘制“波高—弯矩关系曲线”，见图5。在长期分析直接计算结果处作两条平行于波高轴的直线，分别与中拱、中垂合成弯矩曲线相交，交点处的横坐标即为中拱和中垂波浪弯矩的计算波高，分别为(h1)H和(h1)S。

图5 非线性合成弯矩设计值与波高关系Fig.5 The relationship of nonlinear total design moment and wave height

这里需要说明的是，由于极限工况下海况极高，伴随大波高产生的非线性应在载荷响应中体现出来，此时弯矩的中拱值与中垂值不再相等，因此，本文认为在计算极限工况中的弯矩响应应分别对应中拱、中垂有两个计算波高，即(h1)H和(h1)S。

此时，利用规则波中三维非线性水弹性时域程序对这两个波高下的工况进行计算，然后通过数字滤波技术分别得到中拱波浪弯矩(MW)H及中垂波浪弯矩(MW)S。

4.2 砰击弯矩设计值的计算

极限工况由于海况高，此时非线性因素影响更为剧烈，因此砰击弯矩在合成弯矩中所占比重更大。但目前国内现行军规对极限工况下砰击弯矩的考虑不够充分(取波浪弯矩的20%)，且无法体现出艏部线型变化对砰击弯矩设计值的影响，因此，本文建议应采取国外规范的方式通过船艏外张面积对砰击弯矩中垂值进行计算[1]。

极限工况下中垂状态的砰击弯矩表示为任意横剖面的中垂波浪弯矩乘以系数：

(13)

其中，系数FD由表5确定。

表5 系数FD

表5中：AS为下图中两倍阴影部分面积，通过以下公式计算：AS=ba0+0.1L(a0+2a1+a2)。其中，b、a0、a1、a2所示长度如图6。

图6 船艏外飘Fig.6 The picture of bow flare

此外，国外规范中没有关于中拱状态下砰击弯矩的，因此，本文通过理论计算和试验结果的比较分析，认为准则中巡航工况下计算中拱砰击弯矩的方法较为合理，即位于中拱状态的船舯剖面处的砰击弯矩取中垂状态砰击弯矩计算值的0.4：

(14)

4.3 合成弯矩设计值的计算结果比较

本文基于修改后的规范流程，重新计算了目标船巡航和极限工况下的合成弯矩值，并与直接计算结果和规则波理论结果进行比较，见表6，其中极限工况波浪弯矩计算航速取5 kn，中垂、中拱状态下计算波高分别为(h1)H=18.26 m和(h1)S=28.43 m。

表6 不同方法得到的合成弯矩设计值的比较

Table 6 The comparison of design total moment based on different methods

MN·m

通过比较后发现，采用本文修改后的规范算法得到的设计值，与之前相比，结果与直接计算方法结果更为接近，因此，也说明本文对规范提出的修改建议具备一定的合理性。

5 结论

本文阐述了借助不规则波中水弹性理论对水面舰船设计载荷进行长期预报的方法，采用半解析法对时域延迟函数进行了求解，并提出一种能够计及结构弹性效应的非线性设计载荷的直接计算方法，并对现行军规不足之处提出修改建议，所得主要结论如下：

1) 现行规范中极限工况对砰击的贡献考虑不足，且计算航速过高，因此建议进行高海况的模型试验时，应降低航速以避免螺旋桨出水的情况发生；

2) 本文提出的直接计算方法能够有效地考虑船体线型、弹性效应、非线性因素的影响，通过比较后发现能够应用于工程当中；

3)本文提出的新的计算流程弥补了旧的准则砰击弯矩计算不准的不足，此外极限工况中的两个计算波高，有效地考虑了高海况带来的非线性因素影响。

[1]Rules and regulations for the classification of naval ships[S]. UK: Lloyd’s Register, 2011.

[2]田超. 航行船舶的非线性水弹性理论与应用研究[D]. 上海: 上海交通大学, 2007. TIAN Chao. Study on the theory and applications of nonlinear hydroelasticity of ships with forward speed[D]. Shanghai: Shanghai Jiaotong University, 2007.

[3]RAY M C, BATRA R C. Transient hydroelastic analysis of sandwich beams subjected to slamming in water[J]. Thin-walled structures, 2013, 72: 206-216.

[4]LAVROFF J, DAVIS M R, HOLLOWAY D S, et al. Wave slamming loads on wave-piercer catamarans operating at high-speed determined by hydro-elastic segmented model experiments[J]. Marine structures, 2013, 33: 120-142.

[5]范从军, 梁书秀, 孙昭晨. 时域内规则波作用下竖直板的水弹性响应[J]. 海洋工程, 2013, 31(5): 37-44. FAN Congjun, LIANG Shuxiu, SUN Zhaochen. Hydroelastic response of a vertical plate under regular wave action in time domain[J]. The ocean engineering, 2013, 31(5): 37-44.

[6]JIAO Jialong, REN Huilong, SUN Shuzheng, ADENYA C A. Investigation of a ship’s hydroelasticity and seakeeping performance by means of large-scale segmented self-propelling model sea trials[J]. Journal of Zhejiang university-science A: applied physics & engineering, 2016, 17(5): 468-484.

[7]KIM Y, AHN I G, PARK S G. Extraction of the mode shapes of a segmented ship model with a hydroelastic response[J]. International journal of naval architecture and ocean engineering, 2015, 7(6): 979-994.

[8]MARóN A, KAPSENBERG G. Design of a ship model for hydro-elastic experiments in waves[J]. International journal of naval architecture and ocean engineering, 2014, 6(4): 1130-1147.

[9]邹明松, 吴有生, 司马灿, 等. 声介质中船舶三维水弹性力学时域分析技术[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集(上册). 舟山, 2013.

[10]CAO Yusong. A procedure for evaluation, assessment, and improvement of added mass and radiation damping of floating structures[C]//Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering. Portugal, 2008: 163-172.

[11]CHEN Zhanyang, REN Huilong, LI Hui, et al. Experimental and numerical analysis of bow slamming and whipping in different sea states[J]. Journal of ship mechanics, 2012, 16(3): 246-253.

[12]中国船舶工业总公司第七研究院第七〇二研究所. GJB/Z 119-99 水面舰艇结构设计计算方法[S]. 北京: 中国人民解放军总装备部, 1999.

Direct calculation method for nonlinear design loads of warship based on hydroelasticity theory

CHEN Zhanyang1，GUI Hongbin1，REN Huilong2

(1. School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China; 2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

The calculation of the warship design load of the military rules of all countries in the world depends on rigid theory at present. However, with the day-by-day increase of the principal dimensions of a warship, the elastic effect of the hull on load responses has drawn the attention of designers. International calculation methods on the design load were compared with domestic calculation methods in the aspects of hydroelastic theory and tests. The evaluation methods from the domestic rule do not take full account of the importance of slamming load. Therefore, on the basis of three-dimensional nonlinear time-domain hydroelastic theory, the prediction method of load responses of ship in irregular waves was studied, and a direct calculation method of the nonlinear design load was proposed. Finally, on the basis of the direct calculation method, a new calculation process of design load of warship was presented. A comparison between experimental and theoretical results shows that the design loads based on the new calculation process are in good agreement with the direct calculation results. The effectiveness and accuracy of the new calculation process of design load are demonstrated.

hydroelasticity; nonlinear; long-term prediction; design loads; direct calculation method

2015-07-21.

时间：2016-12-12.

国家自然科学基金项目(51509062)；山东省自然科学基金项目(ZR2014EEP024)；海洋工程国家重点实验室(上海交通大学)开放课题项目(1416)；威海市大学共建项目(2015DXGJMS009)；中央高校基本科研业务费专项(HIT.NSRIF.201727).

陈占阳(1984-),男,博士,讲师. 任慧龙(1965-),男,教授,博士生导师.

陈占阳,E-mail:chen_1228@163.com.

10.11990/jheu.201507066

U661.73

A

1006-7043(2017)01-0037-06

陈占阳,桂洪斌,任慧龙. 舰船非线性设计值的水弹性直接计算方法[J]. 哈尔滨工程大学学报， 2017, 38(1): 37-42. CHEN Zhanyang，GUI Hongbin，REN Huilong. Direct calculation method for nonlinear design loads of warship based on hydroelasticity theory[J]. Journal of Harbin Engineering University, 2017, 38(1): 37-42.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.0920.010.html