基于拉盖尔函数的电子节气门模型预测控制研究＊

秦洋洋吴光强,2郭晓晓

（1.同济大学，上海 201804；2.东京大学，生产技术研究所，东京 153-8505）

基于拉盖尔函数的电子节气门模型预测控制研究＊

秦洋洋1吴光强1,2郭晓晓1

（1.同济大学，上海 201804；2.东京大学，生产技术研究所，东京 153-8505）

建立面向电子节气门控制器设计的线性模型，并在模型预测控制框架下设计了包含状态变化和控制量变化的增广状态空间模型。在满足电子节气门的系统约束条件下，利用拉盖尔函数特性，对控制量进行拉盖尔多项式近似转化，从而消除控制时域，降低算法复杂性。仿真试验表明，基于拉盖尔多项式的模型预测控制方法能够实现电子节气门的跟踪控制，并降低系统计算量。

1 前言

电子节气门是汽车发动机的重要控制部件，其控制系统基本目标是节气门开度能够快速精确且超调尽可能小地到达期望目标位置，节气门开度的精确控制可以提高燃油经济性，减少排放，迅速的系统响应，可获得满意的操控性能。因此，节气门的控制对汽车的行驶安全性、动力性、平稳性及经济性具有重要影响。

电子节气门通过传感器、控制器和驱动装置实现加速踏板和节气门之间的连接，替代了传统的机械式连接。为了满足节气门的控制要求，文献中提出了许多控制方法，主要包括模糊PID控制[1]、神经网络控制[2～3]、滑模控制[4～5]、反步法控制[6～7]、输出反馈控制[8]、时间最优控制等[9]。由于排放法规的日益严格和人们对车辆舒适性、动力性的期望越来越高，因此进一步研究提高电子节气门控制性能的控制方法是很有必要的。

本文针对电子节气门的控制要求，建立面向模型预测控制设计的电子节气门线性离散模型，针对传统模型预测控制系统在线求解精度与速度矛盾问题，采用拉盖尔函数近似控制信号以降低在线优化复杂度。

2 预测模型设计

2.1 电子节气门系统模型

模型预测控制是基于模型的控制算法，因此需要建立电子节气门的数学模型，以进行模型预测控制器的设计。电子节气门主要由驱动电机、减速齿轮组、复位弹簧、节气门体及节气门开度传感器[10]组成，其结构如图1所示。

图1 电子节气门结构示意

根据基尔霍夫定律、电磁感应定律、磁场对载流线圈的作用定律可得节气门电机的电枢电路[1]方程为：

式中，Ra和ia分别为电机的电阻和电流；La为电机电感；Vb和kb分别为电机的反电动势和反电动势常数；Ea为电机输入电压；θm为电机旋转角度；Tm为电机转矩；kt为转矩常数。

式（1）经数学运算，并且考虑到电机的电感很小，可忽略不计，即La=0，则有：

忽略齿轮间隙的影响，则节气门转角θ与电机转角θm之间的转换关系为：

式中，n是减速齿轮组传动比。

由式（2）和式（3）可得电机转矩表达式：

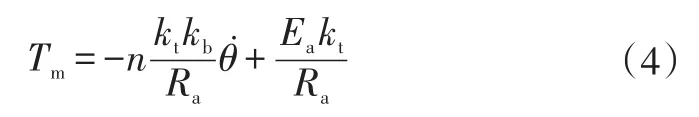
根据广义牛顿定律，忽略负载扭矩、库伦摩擦及其它非线性因素，可得节气门的运动学方程：

式中，J是折算后系统总的等效转动惯量；Tsp为复位弹簧扭矩；Td为摩擦扭矩。

式中，ksp是复位弹簧系数，kd是粘性摩擦系数。

2.2 增广状态空间模型设计

由前文可知，电子节气门系统实际为一单输入单输出系统，其输入输出离散传递函数标准形式可设为：

引入积分环节以消除静态误差[11]，选择增广状态变量：

则系统增广状态空间模型为：

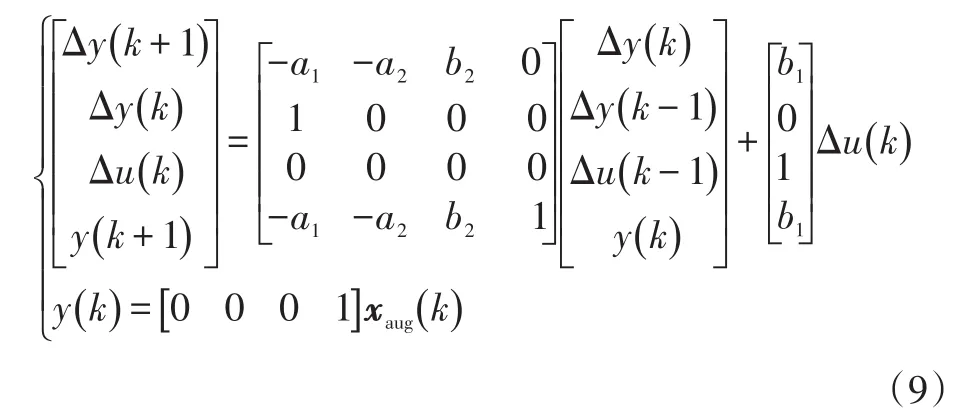
3 预测模型拉盖尔函数转化

传统模型预测控制算法是对式（9）所示系统，根据相应性能指标函数，转化成以控制量为优化变量的二次规划求解过程，文献[12]指出，预测时域和控制时域越大，所求解出的控制结果越精确，然而由于模型预测控制算法具有在线优化的特点，其控制时域及预测时域并不能过大，否则系统实时性将迅速降低，因此利用拉盖尔函数特性对控制量进行近似转化，从而取消控制时域，以降低算法复杂性。

对拉盖尔函数性质分析，n阶离散拉盖尔函数满足[13]：

式中，0≤a＜1是比例因子。

对离散拉盖尔函数进行逆Z变换，得：

ln(m)满足：

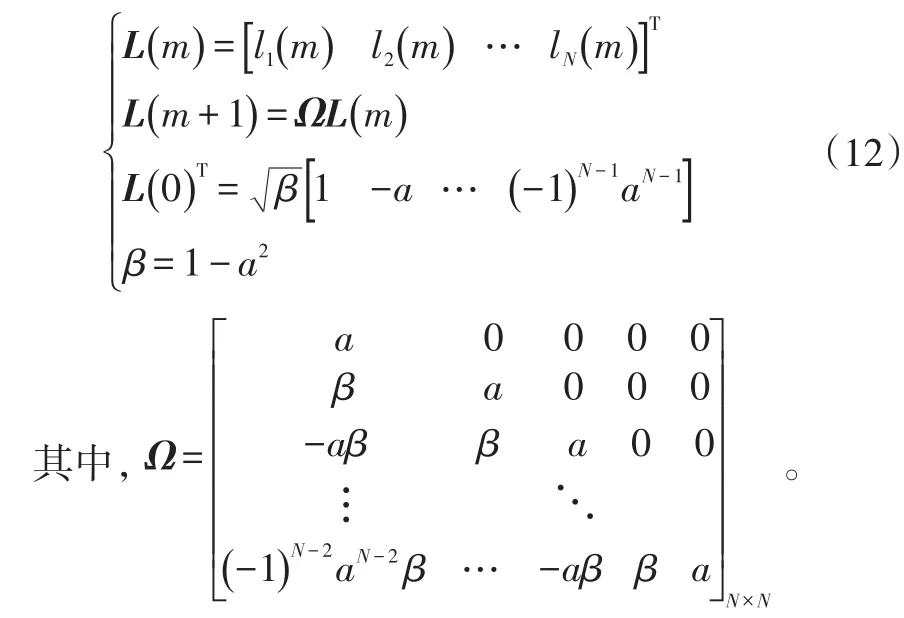
则控制信号变化量可用拉盖尔函数近似表示[14]，随着多项式项数增加，式（13）多项式收敛于实际控制信号变化量。

式中，N为多项式展开项数；是采样k时刻的系数函数；

对于式（9）所示系统，其预测模型可转化为：

4 模型预测控制求解

4.1 控制目标函数分析

设系统性能指标函数：

由式（13）可知：

l()m在时域内同样满足正交性，即：

因此，式（15）性能指标函数等价于：

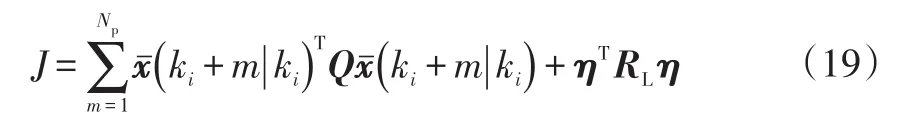
式中，Q=CTC。

代入式（19）可得：

忽略与优化变量无关的常数项，则算法求解转化为在每次预测时间域里的二次规划问题求解预测控制序列。

4.2 系统控制要求及约束处理

电子节气门的具体量化控制要求为[6]：上升时间应不超过100 ms，调节稳定时间小于40 ms，即电子节气门从上升到达稳态的总时间不大140 ms，控制器应使节气门挡板不碰撞限位，即要求零超调，同时要求稳态误差在±2%内。

由于电子节气门驱动电机的饱和限制，电子节气门系统输入电压必须限制在-12～+12 V，且电压变化速率不能过大以确保控制动作的平顺性，即控制器必须满足以下约束条件：

对以上约束条件，转化成矩阵形式：

因此，在MPC的框架下，电子节气门系统控制策略设计最终转化为式（24）带约束的在线二次优化问题。

求解式（24）可得预测控制时域下的控制序列，对于求出的控制序列，只选取其中第1个控制量作为当前控制器输出，下一时刻基于当前系统状态重新求解上述约束优化问题，实现在线滚动优化计算。

5 仿真分析

为了验证所设计的节气门位置跟踪的线性模型预测控制器的功能和有效性，在MATLAB/Simulink中搭建节气门的数学模型，并进行离线仿真试验。节气门系统的模型参数如表1所列。

表1 节气门系统模型参数

控制系统中，a=0.7，N=4，rw=0.3，Np=46，采样步长为1 ms，为验证该算法可行性与优越性，采用传统模型预测控制算法[15]作对比，控制时域Nc=4。

图2～图5所示为期望节气门角度作幅值θd=1rad阶跃变化的跟踪响应，基于拉盖尔函数模型预测控制算法（以下简称改进算法）与传统模型预测控制算法（以下简称传统方法）在响应、控制量、控制量增量及系统求解时间等方面的对比情况。

图2 阶跃信号系统响应

图3 阶跃信号控制量曲线

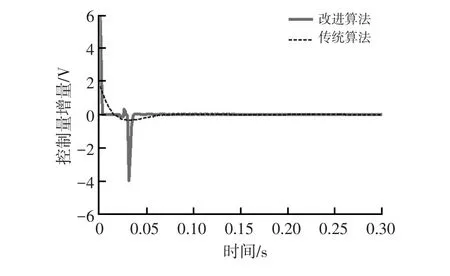
图4 阶跃信号控制量增量曲线

图5 阶跃信号系统求解时间曲线

由图2可知，应用改进算法没有超调，而传统模型预测控制算法系统却发生超调现象。改进算法能更快达到稳态，在40 ms左右稳定，而传统模型预测控制算法在100 ms左右才达到稳定。由图3和图4可知，两种算法都满足约束条件，传统模型预测控制算法控制量更平滑，但可以通过改变控制量速率的上下限来提升改进算法控制动作的平滑性。由图5可知，改进算法求解时间相对传统算法稳定，而传统算法求解时间波动较大，这不利于实际控制系统设计，而两者求解时间数值差别不大是因为传统算法控制时域及预测时域不大，要取得和改进算法相同的效果，需要增加控制时域和预测时域，加长求解时间。

图6～图9所示为期望节气门频率1 Hz、幅值θd=1rad正弦信号时的跟踪响应。

图6 正弦信号系统响应

图7 正弦信号控制量曲线

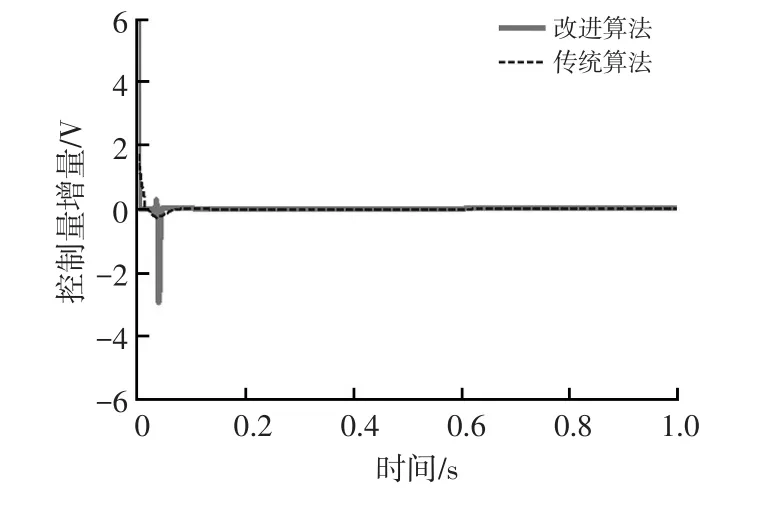
图8 正弦信号控制量增量曲线

由图6～图9正弦信号系统响应对比进一步显示改进算法的优越性，在动态响应方面（图6），改进算法优于传统模型预测控制算法，其正弦跟踪响应误差在2%以内，而传统算法误差较大；动态响应系统求解时间波动情况（图9）方面，改进算法也优于传统算法。

图9 正弦信号系统求解时间曲线

6 结束语

建立节气门系统模型，并设计包含状态量变化及控制量变化的增广状态空间模型以使控制系统消除稳态误差，针对传统模型预测控制算法求解时间和控制精度矛盾问题，设计了基于拉盖尔多项式近似的模型预测控制算法，取消了控制时域，改善了控制系统性能。仿真结果表明，所设计的控制算法能很好的满足电子节气门控制需求，且相较于传统模型预测控制算法得到了改善。

1 Yang C.Model-Based Analysis and Tuning of Electronic Throttle Controllers.SAE Technical Paper,2004-01-0524: 8～11.

2 Baric M,Petrovic I,Peri N.Neural network based sliding mode controller for a class of linear systems with unmatched uncertainties.41st IEEE Conference on Decision and Con⁃trol,Las Vegas,2002:967～972.

3 毛六平，王耀南.基于模糊高斯基函数神经网络的电子节气门控制的仿真研究.电气应用,2006,25（11）:39～43.

4 Hashimoto E,Ishiguro T,Yasui Y,et al.High Reliability Electronic Throttle System Design.SAE Technical Paper, 2003-01-0708:1～9.

5 Dagci O H,Pan Y,Ozguner U.Sliding mode control of elec⁃tronic throttle valve.Proceedings of the American Control Conference,Washington D.C.,2002:1996～2001.

6 宋同好.基于Backstepping的电子节气门控制：[学位论文].长春:吉林大学,2009.

7 陈虹，胡云峰，郭宏志，等.基于Backstepping方法的电子节气门控制.控制理论与应用,2011,28（4）:491～496.

8 胡云峰，李超，李俊，等.基于观测器的输出反馈电子节气门控制器设计.自动化学报,2011,37（6）:746～754.

9 Vasak M,Baotic M,Morari M,et al.Constrained optimal control of an electronic throttle.International Journal of Con⁃trol,2006,79（5）:465～478.

10 朱二欣.电子节气门控制系统的开发研究：[学位论文].长春:吉林大学,2005.

11 邹涛，丁宝苍，张端.模型预测控制工程应用导论.北京：化学工业出版社，2010.

12 Garcia C,Prett D,et al.Model predictive control:theory and practice-a survey.Automatica,1989,25（3）:335～348.

13 Wahlberg B.System identification using Laguerre models.Automatic Control IEEE Transactions on,1991,36（5）: 551～562.

14 Wang Liuping.Discrete model predictive controller design using Laguerre functions.Journal of Process Control,2004, 14（2）:131～142.

15 许芳.快速模型预测控制的FPGA实现及其应用研究：[学位论文].长春：吉林大学，2014.

（责任编辑 晨 曦）

修改稿收到日期为2016年7月20日。

Model Predictive Control Study of Electronic Throttle Based on Laguerre Functions

Qin Yangyang1,Wu Guangqiang1,2,Guo Xiaoxiao1
（1.Tongji University,Shanghai 201804;2.Institute of Industrial Science,the University of Tokyo,Tokyo 153-8505）

To meet the needs of following control of electronic throttle and improve the efficiency of control algorithms,a linear model facing controller design has been built,meanwhile an augmented state space model including changes of state and controlled values on the basis of model predictive control has also been designed.On the restrictions of electronic throttle,controlled variable has been approximately converted using the characteristic of Laguerre functions, which can eliminate control horizon and reduce complexity of control algorithms.Besides,an optimal control sequence using model predictive control based on Laguerre functions was created,which in this way can not only guarantee the dynamic performance of following control,but also reduce the amount of calculation.The simulation showed that the approach of model predictive control using Laguerre functions can better fulfill the following control of electronic throttle and at the same time the calculation amount of the whole system has been decreased.

Laguerre functions,Electronic throttle,Model predictive control

拉盖尔函数 电子节气门 模型预测

U464.11+2

A

1000-3703（2017）01-0033-05

上海汽车工业科技发展基金会项目（1526）。