一类时间和位移约束的变加(减)速运动问题的求解
2017-02-15赵思迪董冰冰
赵思迪 董冰冰 张 冰
(石家庄第二中学 河北 石家庄 050043)
一类时间和位移约束的变加(减)速运动问题的求解
赵思迪 董冰冰 张 冰
(石家庄第二中学 河北 石家庄 050043)
列车运动模型常分为单质点和多质点两类,出于简化问题目的,采用单质点模型针对列车区间运行控制问题中的运动现象进行了分析.列车的牵引和制动力是列车运行控制的输入变量,而位移和速度是列车的状态变量,状态约束是线路限速和区间时间.首先根据最小能耗运行策略确定列车运行方式,并建立相应的数学模型;其次,基于软件Matlab数值求解列车距离--速度的关系,并绘制相应计算曲线.
变加(减)速运动 时间和位移约束 列车区间运行 分段函数 数值求解 Matlab编程
1 引言
在物理课程学习中,变加速运动占据重要的位置,特别是对变加(减)速运动时间、位移问题的求解.当考虑运动物体受牵引力、空气阻力和摩擦阻力等非线性力作用时,通过定量分析就显得异常复杂,并且很难得到解析表达式.同时变速运动控制将是未来节能的关键所在.轨道交通是我国最常见的交通方式(如地铁等),其中的列车运行是一种非常典型的变速运动.列车在站间运行时会根据线路条件、自身特性、前方线路状况计算出一个限制速度.列车运行过程中不允许超过此限制速度.在限制速度的约束下列车通常包含4种运行工况:牵引、巡航、惰行和制动,如图1所示.
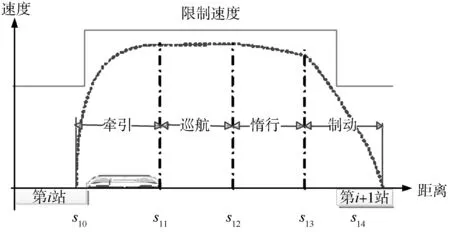
图1 列车站间运行曲线
牵引阶段:列车加速,发动机处于耗能状态.
巡航阶段:列车匀速,所受合力为零,列车需要牵引还是需要制动取决于它当时受到的总阻力.
惰行阶段:列车既不牵引也不制动,运行状态取决于受到的总阻力,发动机不耗能.
制动阶段:列车减速,发动机不耗能.如果列车采用再生制动技术,此时可以将动能转换为电能反馈回供电系统供其他用电设备使用,例如其他正在牵引的列车或者本列车的空调等.
根据相关文献,对列车牵引过程计算分析,可总结出有利于节能的列车运行工况:运行时间一定时,列车以匀速牵引运行克服的基本阻力功最小;列车以最大加速度加速可减小加速过程中的基本阻力功;列车以最大制动能力制动有利于节能;列车制动前惰行以降低制动前的运行速度,有利于减少列车动能的损失;下坡时尽可能利用列车的势能,尽量避免或减少下坡道调速制动.这些节能原则在一定限制条件下可以实施.对于在起伏坡道上的列车运行,尽可能利用列车势能和尽量减少列车动能损失是节能操纵优化的重点.
本文针对某一地铁运行区间,考虑区间限速、坡度、曲线线路以及非线性阻力等因素来分析列车运行操纵规律,求解列车在时间和速度约束下运行距离和速度的关系.
2 列车动力学模型及其约束条件
2.1 列车动力学模型
列车在运行过程中,实际受力状态非常复杂.采用单质点模型是一种常见的简化方法.单质点模型将列车视为单质点,列车运动符合牛顿运动学定律,如图2所示.其受力可分为4类:重力G在轨道垂直方向上的分力与受到轨道的托力抵消,列车牵引力F,列车制动力B和列车运行总阻力W.
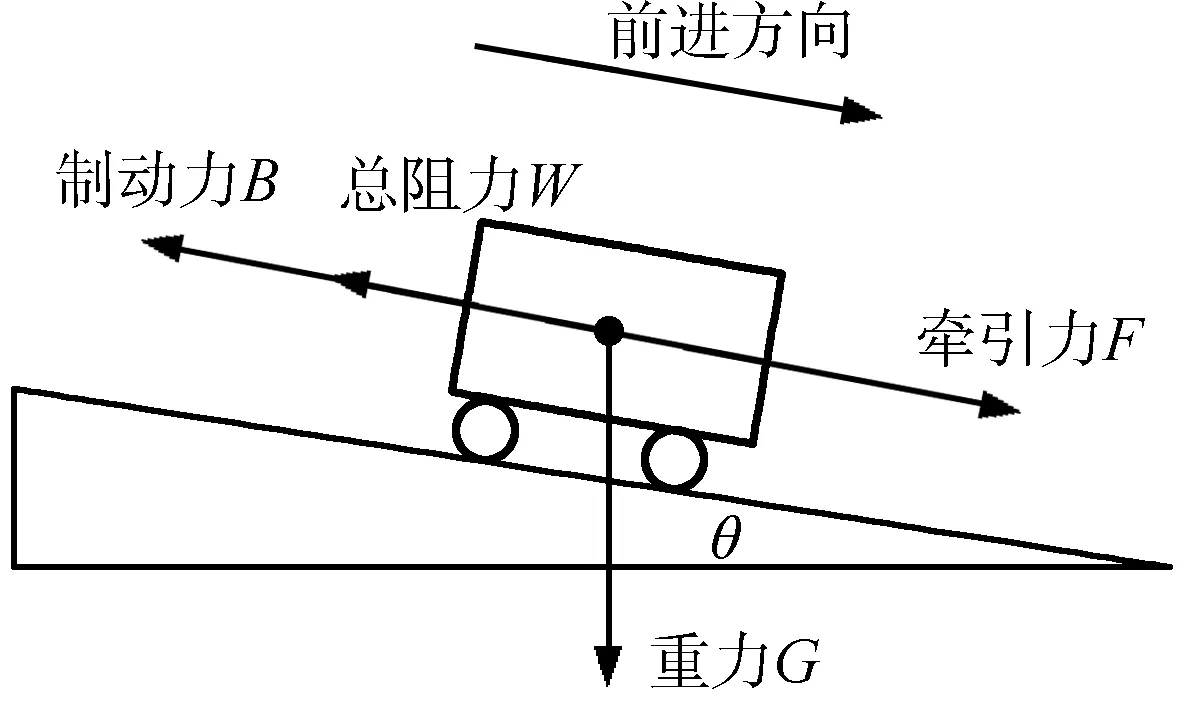
图2 单质点列车模型受力分析示意图
本文选取一实例进行具体的力学建模,具体参数如下:列车质量194.295 t,列车能提供的最大加、减速度为±1 m/s2.列车由A站到B站,全程距离为1 354 m,限定运行时间为110 s,线路区间限速和坡度如图3所示.
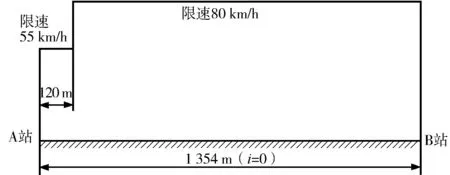
图3 A站至B站区间限速和坡度情况
(1)列车牵引力F
列车牵引力F是由动力传动装置产生的,与列车运行方向相同,驱动列车运行并可由司机根据需要调节的外力.针对本文实际工况,参照相关文献,列车实际输出牵引力(kN)有如下形式
F(v)=μFFmax(v)
(1)
式中,μF是列车实际输出有效功率系数,Fmax是最大牵引力,与列车速度有关,表达形式如下
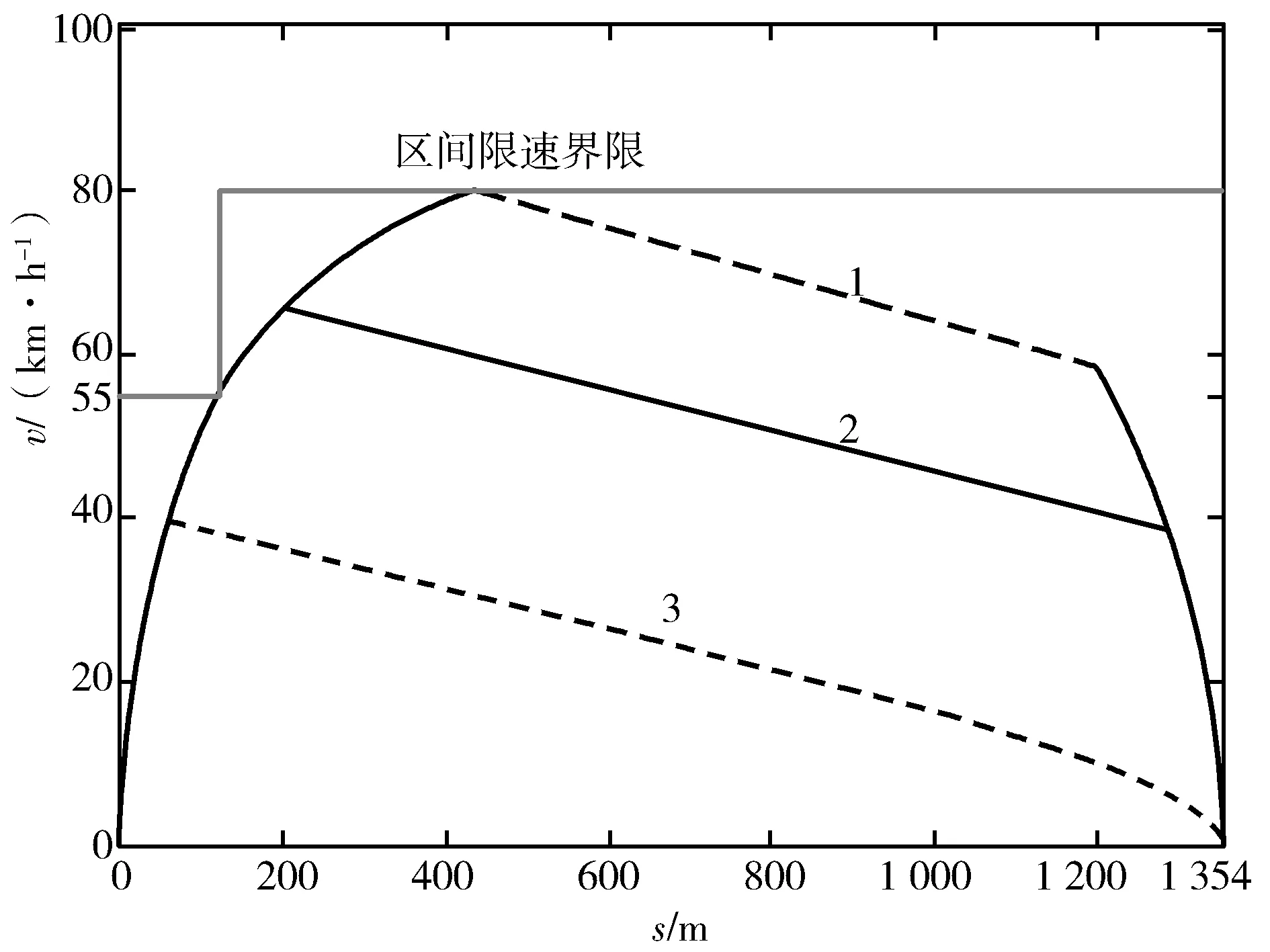
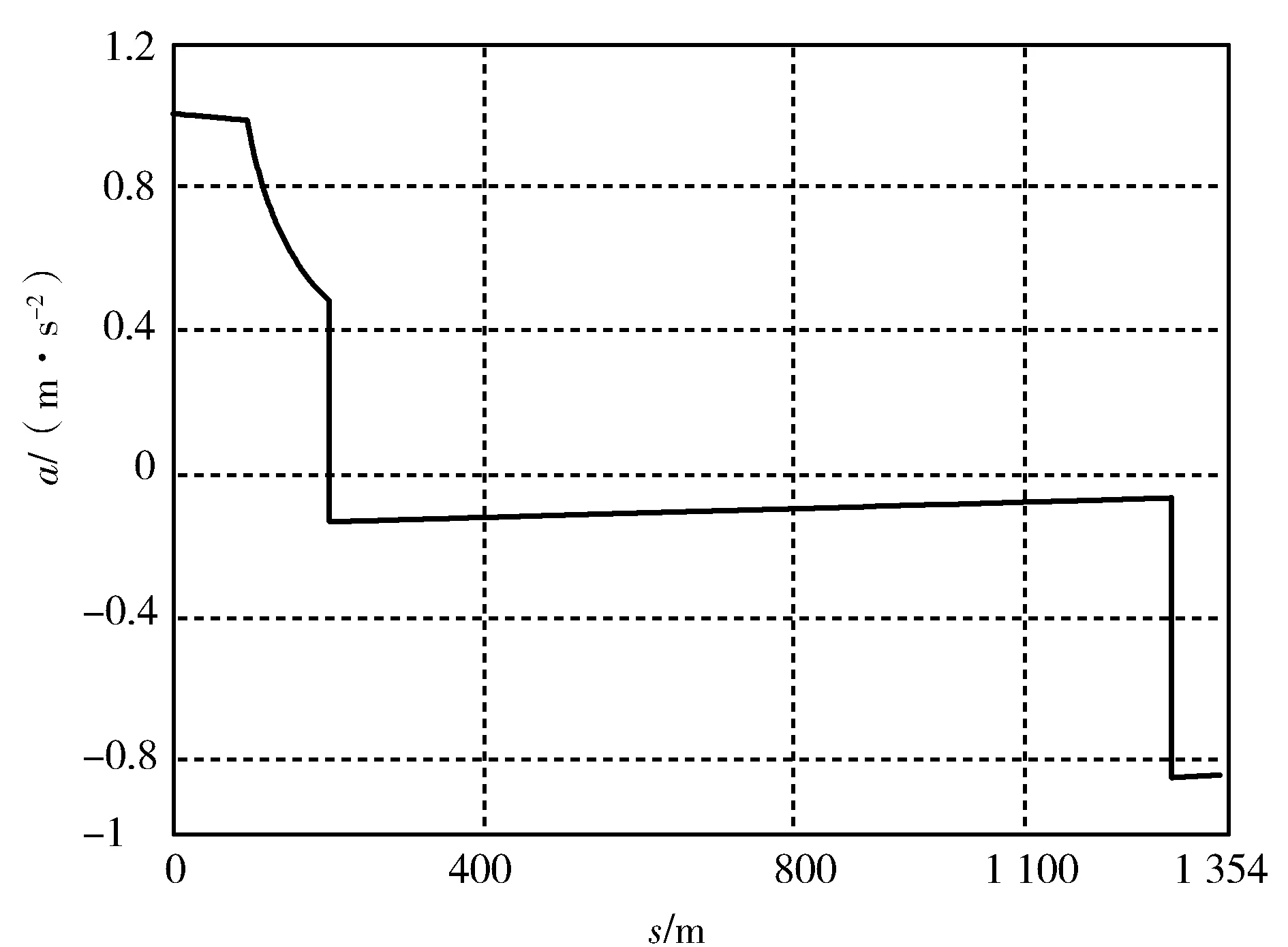
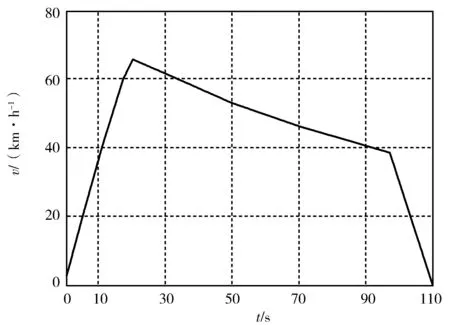
Fmax(v)=203 0 (2) Fmax(v)=-0.002 032v3+0.492 8v2- 42.13v+1 343 51.5 (3) 式中,v是列车速度. (2)列车运行总阻力 列车总阻力是指列车与外界相互作用引起与列车运行方向相反、一般是阻碍列车运行的、不能被司机控制的外力.按其形成原因可分为基本阻力和附加阻力. 1)基本阻力 列车的基本阻力是列车在空旷地段沿平直轨道运行时所受到的阻力.该阻力是由于机械摩擦,空气摩擦等因素作用而产生的固有阻力.具体可分为5部分:车轴轴承间摩擦阻力、轮轨间滚动摩擦阻力、轮轨间滑动摩擦阻力、冲击阻力、气动阻力.因此,基本阻力与许多因素有关,它主要取决于机车、车辆结构和技术状态、轴重,以及列车运行速度等,同时又受线路情况、气候条件影响.由于这些因素极为复杂,而且相互影响,实际应用中很难用理论公式进行准确计算,通常采用以下经验公式来表示基本阻力系数w0(N/kN) w0(v)=2.031+0.062 2v+0.001 807v2 (4) 2)附加阻力 列车由于在附加条件下(通过坡道、曲线、隧道)运行所增加的阻力叫做附加阻力.附加阻力主要考虑坡道附加阻力和曲线附加阻力.附加阻力系数有如下形式, w1=wi+wc (5) 式中,wi是单位坡道阻力系数(N/kN),一般取wi=i,i为线路坡度(‰),wc是列车的曲线阻力系数,主要取决于轨道线路的曲率半径,我国轨道交通一般取600. 综上,列车运行总阻力可按照如下公式计算 (6) 式中,W是总阻力,M是列车质量,g为重力加速度. (3)列车制动力B 制动力B是由制动装置引起的、与列车运行方向相反的、司机可根据需要控制其大小的外力.其 表达式如下 B(v)=μBBmax(v) (7) 式中,μB为实际输出的制动加速度与最大加速度的百分比,Bmax是最大制动力,与列车速度有关,表达形式如下 Bmax(v)=166×1030 (8) (9) 式中,v是列车速度. 2.2 列车运行策略 列车运行策略是在列车运行计算方法的基础上,根据实际需要对列车运行方式进行假设所建立的自动化计算模型.列车运行工况是根据列车运行策略,所釆用的列车牵引、巡航、惰行和制动过程的组合方式.由此可见,列车运行工况的选择取决于列车所釆用的运行策略. 2.2.1 列车运行策略 根据列车运行过程对能耗和时间的具体要求,列车运行策略有3种:最快速度运行策略、最小能耗运行策略和综合优化运行策略,具体如图4所示. 图4 列车运行策略示意图 (1)最小耗能运行策略 最小能耗运行策略是列车基于节能原则的运行方式,大量研究表明,列车能耗最小的运行原则为:加速过程釆用最大牵引力加速,中间运行过程保持巡航运行和尽可能惰行,进站过程釆用最大制动力.另外,在运行时间充裕的情况下, 列车运行速度越低、波动越小,能耗越低.因此,列车最小能耗运行策略可描述为:在规定时间内,以最大牵引力加速至经济速度(vj)(列车以经济速度运行,单位时间的能耗最小),然后以此速度巡航运行至惰行转换点,在时间不足时,列车惰行至制动点,然后采用最大制动力制动,在时间充裕时,可采用惰行至终点(如图4中A-J1-J2-B曲线). (2)最快速度运行策略 最快速度运行策略是列车在运行全程中最大程度发挥牵引和制动能力,确保列车以最短时间完成整个运行过程.因此,列车最快速度运行策略为:列车在牵引过程采用最大牵引力,制动过程采用最大制动力,中间过程速度达到最大限速后,保持最大限速(vL)巡航运行(图4中曲线A-L1-L2-B曲线). (3)综合优化运行策略 综合优化运行策略是在结合上述两种策略的基础上,综合考虑列车运行能耗和速度的优化策略.列车在实际运行中只采取节时或节能运行策略是不现实的,需要采用一种考虑多种因素的综合优化运行策略.列车在运行过程中,一方面,可以通过调节牵引加速度和制动减速度,改变列车运行时间;另一方面,列车在运行至经济速度后,应尽量保持以该速度巡航运行和惰行,以降低能耗(如图4中A-S1-S2-B曲线). 根据本文所选取实例特点(线路距离短、直线,且定时等),故选取第一种最小能耗运行策略,从而建立如下计算模型. 2.2.2 数学建模 T=Tacc+Tcru+Tco+Tbra= (m+n+p+q)Δt=110 s (10) (1)根据所选列车运行策略,4种运行工况分析 1)列车牵引阶段 根据牛顿第二定律可得 (11) 根据已知列车最大加(减)速度为±1 m/s2,可得 得 μ1=0.976 56 (12) 根据式(2)、(3)有 (13) aacc(v)=-0.000 010 213 15v3+ 0.002 458 819 7v2-0.212 373 96v+ 6.729 812 9 51.5≤v≤80 km/h (14) 由于这类变加速运动是多种分段函数问题, 解析求解难度很大,一般采用数值求解.因此首先利用中间插值可得第k时间段内,平均加速度值为 (15) 式中m是自然数,以下k,n,p,q都是自然数. 这样第k段平均速度(其中v0=0)和行驶距离为 vk=vk-1+akΔtk=1,2,3,…,m (16) (17) 式中vk,sk分别是第k段区间上的平均速度和加速度,下同. 2)列车巡航阶段 (18) 3)列车惰行阶段 同式(13)、(14)相同的思路可得 aco=-0.000 234 187 2v2- 0.002 239 2v-0.020 31 (19) 求解过程中采用如下形式 (20) (21) (22) 式中k,n,p都是自然数. 4)列车制动阶段 (23) abra=-0.000 018 07v2-0.006 22v- 0.844 968 97 0≤v≤77 km/h (24) abra=-0.000 685 248 913 68v2+ 0.123 921 375 77v- 6.478 482 656 627 77≤v≤80 km/h (25) (26) (27) (28) 式中q都是自然数. (2)列车运行能耗模型 牵引阶段能耗 (29) 巡航阶段能耗 (30) 列车的总耗能 E=Eacc+Ecru (31) 为了满足最小能耗策略,同时考虑运行区间较短,本文采取的运行策略:最大加速-惰行-最大制动[2~7],约束条件是运行距离为1 354 m,运行时间为110 s,同时在各区段不得超过相应限速.本文基于Matlab软件进行了优化求解,图5给出了运行区间内距离和速度的关系曲线. 图5 A站至B站区间距离与速度关系曲线 图5中,水平直线表示不同区间的限速情况,在0~120 m区间内,限速55 km/h;在120~1 354 m区间内,限速80 km/h.图中曲线1表示了列车以最大牵引力加速到80 km/h(通过计算,加速过程中,当达到55.5 km/h时,距离已超过120 m的距离),然后惰行到58.5 km/h左右,最后以最大制动力制动的距离-速度关系.从图中可以看出,这种运行策略所用时间最短,仅需要91 s就可到达B站.曲线2表示了列车以最大牵引力加速到66 km/h时,然后惰行到38.5 km/h,最后以最大制动力制动的距离-速度关系.从图中可以看出,这种运行策略所用时间满足约束要求,即运行时间为110 s, 即为最终求解的运行策略.曲线3表示了列车以最大牵引力加速到39.4 km/h时,然后惰行到终点的距离-速度关系.从图中可以看出,这种运行策略所用时间最长(运行时间为311 s), 但可以看出这种运行策略最节能. 同时,针对第二种运行控制策略,图6和图7分别给出了列车在A站-B站之间运行时,加速度与运行距离以及速度与时间的关系曲线. 图6 A站至B站区间距离与加速度关系曲线 图7 A站至B站区间运行时间与速度关系曲线 本文基于单质点模型,借助数值编程方法求解了日常生活中常见的列车区间分段变加(减)速运动的优化控制问题.出于节能的目的,采用了牵引-惰行-制动的运行策略,绘制了满足时间约束和距离约束的距离-速度关系曲线.通过编程计算,较好地掌握了数值求解复杂数学问题的思路,为进一步求解复杂变加速运动奠定了基础. 1 石博强,滕贵法,李海鹏,等.Matlab数学计算范例教程. 北京:中国铁道出版社,2004 2 丁勇,毛保华,刘海东,等.列车节能运行模拟系统的研究.北京交通大学学报,2004,28(2):76~81 3 金炜东,靳蕃,李崇维,等.列车优化操纵速度模式曲线生成的智能计算研究,铁道学报,1998,20(5):47~52 4 付印平,高自友,李克平.路网中的列车节能操纵优化方法研究. 交通运输系统工程与信息,2009,9(4):90~96 5 朱金陵,李会超,王青元,等.列车节能控制的优化分析.中国铁道科学,2008,29(2):104~108 6 王峰,刘海东,丁勇,等.列车节能运行的算法及实施技术研究.北京交通大学学报,2002,26(5):13~18 7 王自力.列车节能运行优化操纵的研究.西南交通大学学报,1994,29(3):275~280 赵思迪(1999- ),男,在读高中生. 指导教师:张冰(1981- ),男,中教一级,主要从事中学物理教学及研究. 2016-09-12)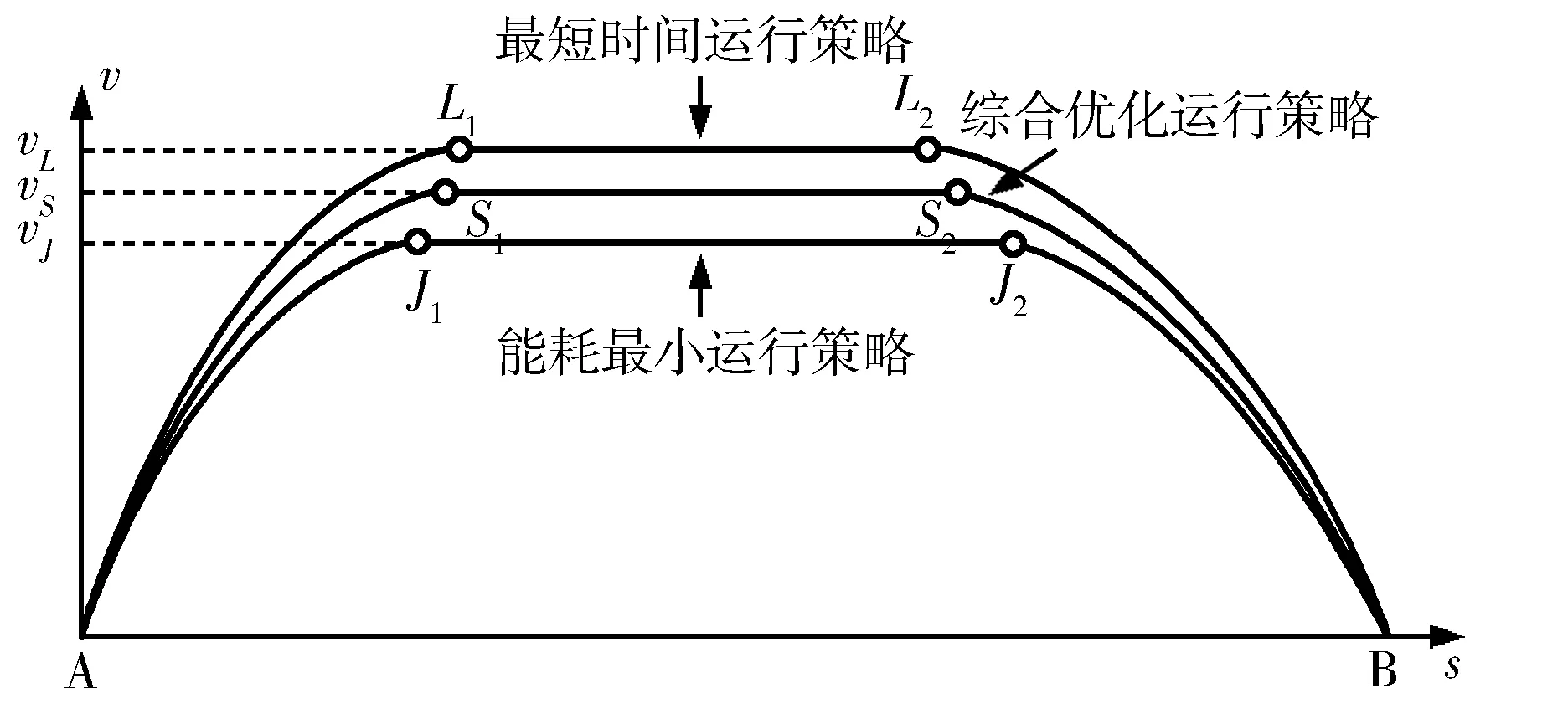
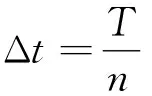
3 数值求解
4 结论
