试谈概率和数理统计知识的教学功能

王溢然

(江苏省苏州中学 江苏 苏州 215007)

试谈概率和数理统计知识的教学功能

王溢然

(江苏省苏州中学 江苏 苏州 215007)

在简述概率与数理统计概念的基础上，结合教学实际指出了它们在中学物理中主要的教学功能.

概率 数理统计 教学功能

数理统计是以概率论为基础，研究随机现象的统计规律性.具体地说就是研究怎样有效地收集、整理有限的资料，并通过数学的分析，对实际问题尽可能地做出最可靠的结论.

概率和数理统计都是数学科学的分支.当前，概率和数理统计知识在中学物理中的直接应用虽然并不多，但它们却有着极为重要的教学意义，应该予以足够的重视.

1 转变观念

这是概率和数理统计知识在教学中最重要的作用.因为在牛顿力学中，如果知道了一个质点的受力情况和初始条件，就可以完全确定它在空间的运动规律(如运动速度、加速度和轨迹等)，因此，根据牛顿力学所得到的是一种确定性规律.牛顿曾经说过这样的话：“自然界的一切现象，全都可以根据力学的原理，用相似的推理一一地演绎出来”.当然，牛顿的话具有局限性也是由于时代局限性的缘故.

学生在力学部分的学习中，对这种确定性规律会随着知识内容逐渐加深印象.尤其是当学生学习了万有引力定律后，知道根据万有引力理论，可以预言神出鬼没的彗星回归；不需要看天空一眼，就能够

在笔尖下发现新的行星…….牛顿力学的魅力在老师的激情演绎下得到了淋漓尽致的发挥.这样，一方面既深深地吸引住了学生，使他们陶醉于牛顿力学的伟大成就之中；另一方面“机械决定论”的世界观、方法论，也在潜移默化中侵袭着学生的头脑，甚至会在学生的头脑中扎根.

直到学习了麦克斯韦关于气体分子的速率分布规律后，学生才认识到，对于有大量分子集体运动所表现出来的宏观特性，是一种或然的结果，它们并不遵循牛顿力学的确定性规律.可以说，这是使学生第一次从原来的“决定论”的方法，转向以概率论为基础的“统计”方法，无疑是一种观念的转变.

2 深化认识

气体分子运动的速率分布，仅是使学生初次认识了物质运动的“或然”性.以后，当学生学习了微观粒子的波粒二象性后，才会进一步认识到概率分布的意义.

根据量子力学的观点，原子的核外电子并非仅处于有一定半径的轨道上，而是可以处于原子核外的整个空间，形成“电子云”一样的分布(图1).

图1 电子在核外的分布

长期以来，学生从接触到浅显的科普读物开始，就对原子结构形成了一个根深蒂固的模型——原子结构像太阳系，中间有一个原子核，电子在原子核外不同的轨道上绕核运动(图2).如今，这个传统的原子结构被打破了——电子并没有确定的轨道，而是呈现一种概率分布规律.因此，这个观点可以认为是学生思想认识上的一次真正的飞跃.

图2 传统的原子结构图

由于微观粒子具有波粒二象性，因此我们可以用波函数Ψ描述电子的运动，在离核不同距离处出现电子的概率(几率)，就由波函数振幅的平方|Ψ|2决定.图3中画出了原子的核外电子轨道和波函数|Ψ|2所对应的关系[1].可见，原来传统理论中的核外电子的轨道，只不过是电子出现概率最大的地方.当波函数|Ψ|2有不同的取值时，它可以对应着电子的跃迁，并伴随着一定的辐射或吸收.这里，充分显示了微观粒子具有完全不同于宏观物体的行为.

图3 原子的核外电子轨道和波函数|Ψ|2

早在1812年，法国著名数学家、天体力学家拉普拉斯(P.S.Laplace)曾经预言：“非常值得注意的是，与游戏中机遇有关的科学知识，将会成为人类知识中一门重要的学科.” 如今，人们都知道以概率为基础的规律普遍存在于自然现象之中，并已被人们发展成非常完美的一门理论.

3 辅助论证

在教学中，还可以利用概率和统计平均的知识，结合有关内容作一些辅助性的论证(或计算).这样，可以使学生对它们形成更为具体和深刻的认识.中学物理中常见的有以下内容.

3.1 分子的无规则运动

分子动理论指出，物质分子始终不停地做着无规则的运动.如果一个学生突发奇想：既然教室里的空气分子做的是无规则运动，那么它们会不会在某个时侯都聚集在教室的某一部分，从而在另一部分呈现“真空”，以致使那边的人窒息呢？

这是一个很有意思的问题.首先，现实生活中从来没有发生过这样窒息的事，其次，也可以通过对概率的计算证明，不可能产生上述这种情况.

可见，这个概率是如此之小，完全可以认为等于零.也就是说，这个学生的假设是不可能产生的.

图4 教室里的空气分子

从上述计算所显示的不可能性，反过来的意思就是说，由于大量分子的无规则运动，它们在教室里一定是均匀分布的.因此，你在生活中用不着担心，房间里的空气分子绝对不会聚集在一个角落，使你感到窒息的.

3.2 分子运动的平均速率

有的学生认为，按照平均速率的定义，它应该是大量分子无规则运动速率的算术平均值，即

由于组成物质的分子是如此之多，它们又始终不停地做着无规则运动，实际情况下是没有办法去测定每个分子运动速率的，那么如何知道它们的平均速率呢？这里，麦克斯韦关于气体分子的速率分布律就有用武之地了.

1859年，麦克斯韦借助几率概念，推导出一个有关气体分子速率分布的函数f(v)，其图像如图5所示.速率在v→(v+Δv)区间内的分子数占总分子数的百分比等于曲线与横轴之间狭条的面积.整个曲线与横轴之间的面积就等于容器内各速率区间内的分子数占总分子数百分比之和.其值应为100%=1，速率在v→(v+Δv)区间内的分子数ΔN=Nf(v)Δv.显然，平均速率的计算需要涉及到高等数学中的微积分运算.

图5 某一温度下速率分布曲线

在初等数学范围内，为了计算某温度下气体分子的平均速率，可以借助实验方法得到的不同速率区间内分子数的比例关系.表1就是教材中列出的在0 ℃和100 ℃时氧分子的速率分布.

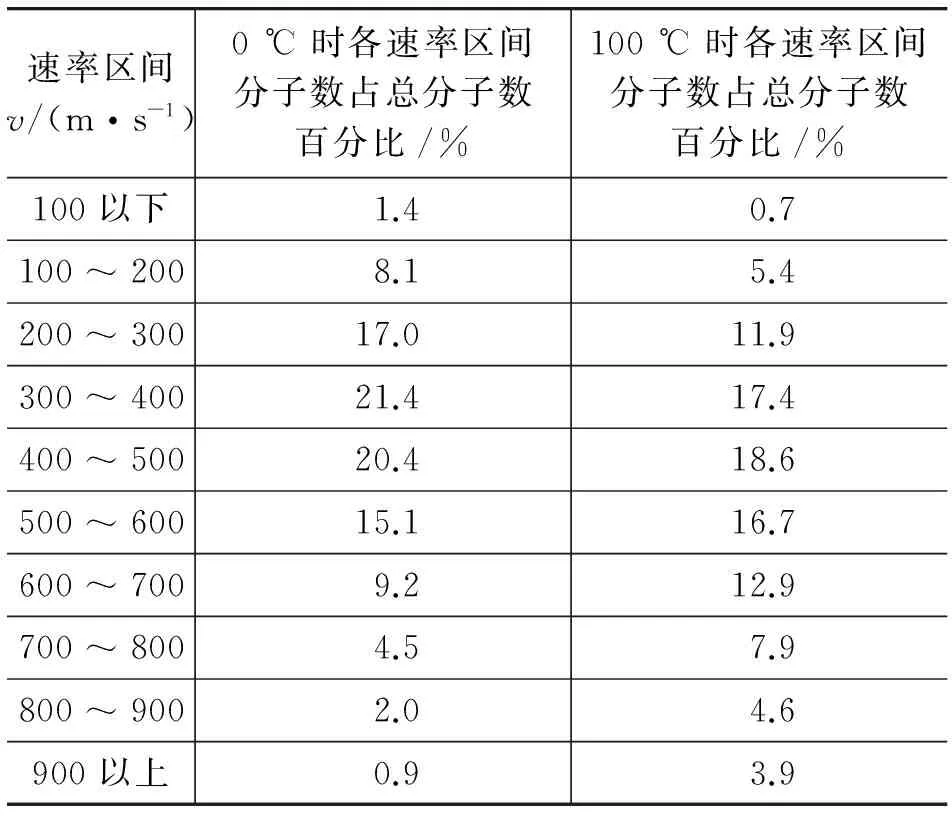
表1 氧分子的速率分布

如果需要计算氧分子0 ℃时平均速率，可以先进行简化[2]：由于分子的无规则运动，假设不同速率区间内的分子都以该区间的中值为平均速率在运动.若对应的分子数以ΔNi表示，总分子数以N表示，则0 ℃时的不同速率和对应的分子数分别为

ΔN1=1.4%N

ΔN2=8.1%N

ΔN3=17.0%N

……

取

v10=900 m/s ΔN10=0.9%N

1.4%v1+8.1%v2+…+0.9%v10=

423.75 m/s

可见，通常情况下气体分子平均速率约为几百米每秒，即其平均速率的数量级为102m/s.

上述这样的简化方法，实际上相当于将原来连续光滑的速率分布曲线转化为常见的条形统计图(简称为直方图)，如图6所示[3].

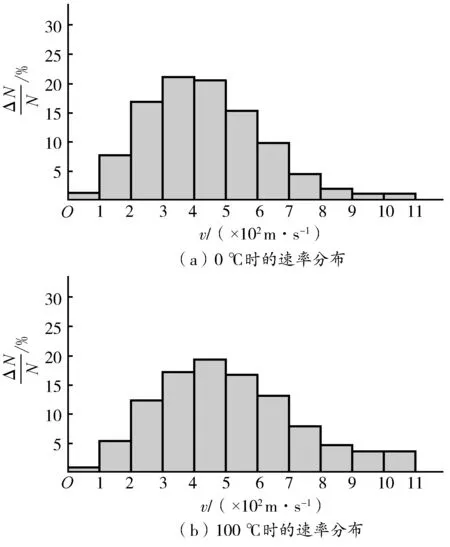
图6 0 ℃时和100 ℃时氧分子的速率分布直方图

3.3 理想气体的压强

根据分子动理论，气体的压强是由于大量气体分子无规则运动碰撞器壁而产生的.这个情况就像密集的雨滴打在伞面上，虽然雨滴对伞面的冲击力是间断而不均匀的，感觉上却像受到持续的恒力作用一样.如图7所示的模拟实验——密集的小弹子落在秤面上，秤面会显示某个比较稳定的压力.显然，气体的压强决不是个别分子的作用，而是大量分子共同作用的一种统计平均效果.

图7 模拟密集的小弹子落在秤面上

沿着这样的思路，借助统计平均概念，采用力学方法就可以进一步认识气体压强的产生及其大小的决定因素了.

假设一个正方形密闭容器中有大量运动粒子，每个粒子质量为m，单位体积内粒子数量n为恒量.为简化问题，我们假定：粒子大小可以忽略，其速率均为v，且与容器各面碰撞的机会均等；与容器碰撞前后瞬间，粒子速度方向都与器壁垂直，且速率不变.

先考虑一个粒子，它以速率v与器壁发生弹性碰撞后，以原速率大小v′反弹(图8).根据动量定理，这个粒子给器壁的冲量大小为

ΔI=mv′-(-mv)=2mv

图8 粒子以v′反弹

设想在器壁上以S为底，以l=vΔt为长作一个柱体(图9),在这个柱体内所包含的粒子总数为

N=nlS=nvΔtS

图9 作柱体分析

则器壁受到总的压力为

所以器壁单位面积受到的压力大小，即压强为

这个关系式实际上就是理想气体的压强公式，联系了粒子的动能，并考虑到分子的速率大小不同取平均值后，上式可以表示为

式中

称为平均平动动能，它是物体(气体)温度的量度.由此可见，理想气体的压强是一个统计平均的结果，它的大小本质上决定于分子密度和平均平动动能.宏观上，一定质量理想气体的压强由其温度和体积所决定.

3.4 布朗运动的分析研究

1872年，英国植物学家布朗发现悬浮在水中的花粉微粒始终不停地运动现象后，曾经难倒了习惯于牛顿力学决定论思想方法的物理学家.直到几十年后，人们才认识到布朗运动的原因——由于这些物质微粒不断受到周围液体分子不均匀碰撞的缘故.那么，怎样才能对微粒的这种无规则运动作进一步的量化研究呢？

下面，我们把布朗运动简化为平面内的无规则运动，采用统计平均的方法作一初步探讨[5].

如果把布朗运动中的固体微粒“拟人化”，它的运动极像一个醉鬼走路：某时刻这个醉鬼从广场某处O(如灯柱)出发，先朝一个方向走上几步，然后换个方向再走上几步，踉踉跄跄、曲曲折折，毫无定规，不断随意地改变着方向(图10).那么如此转折了几百步后，最终离开灯柱究竟有多远？

图10 醉鬼走路

为此，以这个灯柱为坐标原点O，在广场的水平面内建立一个直角坐标系xOy,如图11(a)所示.

假设醉汉开始沿直线Oa走几步到了位置a，线段Oa在两坐标轴上的投影分别为x1和y1，设a点离开原点O的距离为R1，如图11(b)所示，则

接着，醉汉转向走到了位置b，线段ab在两坐标轴上的投影分别为x2,y2，设b点离开原点O的距离为R2,如图11(b)所示，则

由于ab在x轴的投影沿x轴的负方向，式中x2应该取负值.

图11 醉汉离开原点(灯柱)多远？

假设醉汉在这个过程中沿着各个不同方向走了N次，各折线段在x轴和y轴上的投影依次为(x1，x2，…，xN)和(y1，y2，…，yN)，离开坐标原点(灯柱)的距离为R(图12).同理可知，有关系式

R2=(x1+x2+x3+…+xN)2+

(y1+y2+y3+…+yN)2

式中的那些x，y的正与负，由醉汉行走方向是沿着坐标轴的正方向或负方向决定，也即与醉汉离开灯柱或朝着灯柱走的方向决定.

图12 醉汉的行走路径示意图

由于醉汉的运动完全是无规则的，当N值很大时，可以认为其中取正值的x，y个数与取负值的x，y个数大体相同.根据初等代数的法则，计算上式中括号内各项平方时，应该把括号内每一项自乘，并用其他各项与之相乘，即

(x1+x2+x3+…+xN)2=(x1+x2+

x3+…+xN)(x1+x2+x3+…+xN)=

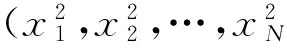
因为醉汉的行走完全是随机的，当行走中转身次数很多时，他向着灯柱走一步和离开灯柱走一步的可能性是相同的，所以在所有交叉项中，数值相同而符号相反的项可以认为是“成对”出现的，它们相加的结果正好抵消.于是，上式就可以写成

(x1+x2+x3+…+xN)2=

这里的x是各段折线在x轴上投影平方的平均值.

同理，对y方向有关系式

(y1+y2+y3+…+yN)2=

于是，可以得到

R2=N(x2+y2)

或

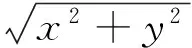
现在，让我们从醉鬼走路的研究中再回到布朗运动，在显微镜下可以看到悬浮的固体微粒做着完全无规则的运动，微粒所经历的是一条非常复杂的曲折路径.虽然微粒运动的无规则性甚于醉汉千百倍，从研究方法来说，两者却是完全类似的.

1905年，爱因斯坦和波兰物理学家斯莫卢霍夫斯基，分别独立地对布朗运动进行了深入的研究.他们根据做布朗运动的微粒在每段时间Δt内的位移，利用统计平均的方法，从理论上找出了布朗运动中的悬浮粒子不规则运动的方均根位移公式.根据这个公式推算出在17 ℃水中的悬浮粒子在1 min里平均位移大约是6 μm.同时，反过来也可以利用所求得的关系测定阿伏加德罗常数N，得到的值为

式中λ为微粒的位移，R为气体常数，T为绝对温度，k为粘滞系数，ρ为微粒半径[6].后来，法国物理学家佩兰和他的同事一起，从1908年到1910年花费了约三年的时间，通过艰苦卓绝的努力，终于出色地完成了对微粒位置和分布规律的测量，证明了实验结果与爱因斯坦理论的一致性，从而奠定了分子动理论的基础.

对布朗运动研究的成功，可以说是20世纪初刚建立的统计力学的一项辉煌成果.在布朗运动的研究中所采用的统计平均方法，具有非常典型的意义.它向人们指出，即使在如此复杂的运动中，利用统计方法同样可以找出一定的规律性.

1 吴翔.文明之源.上海:上海科学技术出版社，2001

2 王溢然，束炳如.中学生物理思维方法丛书：数学物理方法.合肥：中国科学技术大学出版社，2016

3 束炳如，何润伟.普通高中课程标准实验教科书物理·选修3-3.上海：上海科技教育出版社，2005

4 2013年北京高考物理试题

5 王溢然，束炳如.中学生物理思维方法丛书：形象·抽象·直觉.合肥：中国科学技术大学出版社，2016

6 蒋长荣，王骁勇，刘树勇.爱因斯坦与布朗运动.首都师范大学学报(自然科学版)，2005，26(3)：28～32

王溢然(1938- ),男，江苏省物理特级教师，主要从事中学物理教学思维方法研究和新课标教材编写等工作.

2016-07-26)