全非平稳地震动过程的概率模型及反应谱拟合

刘章军， 刘增辉， 刘 威

(1.三峡大学 土木与建筑学院，湖北 宜昌 443002；2.湖北省防灾减灾重点实验室(三峡大学)，湖北 宜昌 443002)

全非平稳地震动过程的概率模型及反应谱拟合

刘章军1,2， 刘增辉1， 刘 威1

(1.三峡大学 土木与建筑学院，湖北 宜昌 443002；2.湖北省防灾减灾重点实验室(三峡大学)，湖北 宜昌 443002)

在强度调制函数基础上，发展了一类全非平稳地震动过程的时-频调制函数。结合平稳地震动过程的功率谱密度函数，建立了全非平稳地震动过程的演变功率谱模型，并根据建筑抗震设计规范确定了模型参数的取值。应用非平稳过程模拟的谱表示-随机函数方法，生成具有完备概率的非平稳地震动加速度过程的代表性时程集合，进而计算代表性时程的平均反应谱。为保证计算平均反应谱与建筑抗震设计规范反应谱的一致性，建议了反应谱容许误差的双重控制准则，即平均相对误差和最大相对误差。研究表明，通过对演变功率谱的3次迭代修正，即可实现计算平均反应谱与规范反应谱拟合的目的，为应用结构随机动力学进行实际工程结构抗震设计提供了依据。

地震动；非平稳过程；时-频调制函数；概率模型；反应谱；抗震设计

作用于工程结构的地震动具有很强的随机性和非平稳性。在以往的抗震分析中，由于强度非平稳模型的简便性以及物理意义的明确性，人们更多地关注地震动强度非平稳特性对结构随机地震反应的影响[1]。近些年来，大量研究表明[2-3]：地震动的全非平稳性(包括强度非平稳和频率非平稳)对结构进入非线性阶段后的力学行为有显著影响。目前，时-频全非平稳地震动模型是地震动输入领域研究的热点[4-5]。此外，在复杂工程结构的非线性抗震分析中，一般选择几条地震动记录或人造地震动时程进行确定性的结构动力学分析。然而，确定性的动力分析方法无法全面地反映地震动的随机性和结构地震反应的丰富概率信息，造成这一困境的主要原因：①需要应用经典的随机模拟方法生成大量的地震动输入时程，地震动时程的数量可能达到数千上万个，这极大地增加了复杂工程结构随机地震反应分析的计算工作量；②为了精细化地评价复杂工程结构的抗震可靠性，需要获取结构反应的高阶统计量或概率密度函数，这对于以二阶统计量为特征的经典随机振动理论仍是一个挑战。正因如此，经典随机振动理论仍未能应用于复杂工程结构非线性抗震分析的实践中。

同时，在现阶段，各类结构抗震设计规范均以反应谱作为确定地震动输入的依据，通常要求输入地震动时程的反应谱按照一定精度拟合或包络规范反应谱[6]。在本质上，规范反应谱是对大量实际地震记录的反应谱进行统计分析并结合经验判断加以定义的，是从工程结构设计的角度，在统计意义上对地震动特性的把握。而随机地震动模型则可应用合理的模拟方法获得地震动时程的样本集合，并通过地震动时程的平均反应谱拟合规范反应谱。从而，使规范反应谱与随机地震动模型在本质上具有一致性。因此，如何由规范反应谱生成与之相应的地震动时程集合，是地震工程理论研究和工程实践的重要问题[7]。事实上，随着现代结构随机动力学理论的日趋完善，随机地震动模型研究与工程应用已得到了深入的发展[8-11]。

基于上述研究进展，笔者首先在非平稳过程的谱表示理论基础上，利用随机函数的思想，建议了一类全非平稳地震动过程模拟的谱表示-随机函数方法[12]，实现用一个基本随机变量表达地震动过程的目的。其次，在强度调制函数基础上，发展了一类全非平稳地震动过程的时-频调制函数，并结合平稳地震动过程的功率谱密度函数，建立了全非平稳地震动过程的演变功率谱模型，其模型参数取值可根据建筑抗震设计规范[13]来确定。以谱表示-随机函数方法和时-频调制函数构造的演变功率谱模型为基础的全非平稳地震动概率模型，其优点之一在于通过选取基本随机变量的离散代表点，直接获得具有给定赋得概率的非平稳地震动过程的代表性时程集合，从而实现在代表性时程集合的层次上考察地震动过程。然而，由概率模型生成的地震动代表性时程集合的平均反应谱仍无法与规范反应谱拟合。事实上，采用任何随机方法求出的反应谱曲线与规范反应谱在不同周期点上的数值差别较大，尤其在长周期部分的差别更大[14]。为了保证计算平均反应谱与规范反应谱的一致性，本文采用反应谱容许误差的双重控制准则，通过对演变功率谱的3次迭代修正，实现了计算平均反应谱与规范反应谱拟合的目的，从而为结构随机地震反应分析和抗震设计提供了合理的地震动输入时程。此外，全非平稳地震动概率模型的另一优点是与概率密度演化理论相结合，可以实现复杂工程结构的随机地震反应与抗震可靠性的精细化分析。

1 非平稳过程模拟的谱表示-随机函数方法

根据Priestley非平稳过程的演变功率谱理论，一个单变量、一维、零均值的实非平稳过程f0(t)可表示为：

(1)

式中，A(t,ω)是确定性的调制函数；Z(ω)是正交增量的复过程，满足如下的关系：

E[dZ(ω)]=0

(2)

E[dZ(ω)dZ*(ω)]=S(ω)dω

(3)

E[dZ(ω)dZ*(ω′)]=0，ω′≠ω

(4)

dZ(-ω)=dZ*(ω)

(5)

式中，E[·]表示数学期望，符号“*”表示取共轭复数。

于是，自相关函数可表示为：

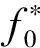
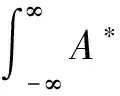
(6)

若令τ=0，则有：

(7)

其中

(8)

称为非平稳过程f0(t)的双边演变功率谱密度函数，S(ω)则为相应平稳过程的双边功率谱密度函数。对于实非平稳过程，可假定A(t,ω)是一个关于频率ω的实的偶函数，即A(t,-ω)=A(t,ω)。

在上述非平稳过程的演变功率谱理论基础上，文献[15]建议了一类实非平稳过程模拟的谱表示方法：

f(t)=

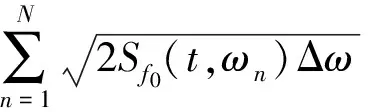
(9)

式中，f(t)为模拟的非平稳过程；ωn=nΔω，频率间隔Δω需足够小，以便满足精度要求。

在式(9)中，Xn与Yn(n=1,2,…,N)为标准正交随机变量，满足如下的基本条件：

E[Xn]=E[Yn]=0，E[XmYn]=0

(10a)

E[XmXn]=E[YmYn]=δmn

(10b)

式中，δmn为Kronecker记号。

于是，实非平稳过程模拟的均方相对误差可表示为：

(11)

式中，ωu=NΔω为计算截断频率；Τ为非平稳过程的持续时间。一般地，计算的均方相对误差ε(N)≤5%。

利用随机函数的思想，可将标准正交随机变量{Xn,Yn}表示为随机函数的形式：

Xn=hn(Θ)，Yn=gn(Θ)，n=1,2,…,N

(12)

式中，hn(·)和gn(·)为确定性的函数形式，Θ为基本随机变量。显然，式(12)必须满足基本条件式(10)。

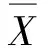
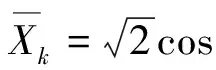
k=1,2,…,N

(13)

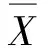
2 非平稳地震动过程的调制函数

非平稳地震动过程的调制函数一般分为强度调制型和强度与频率调制型两种，其中强度与频率调制函数也称时-频调制函数。

2.1 强度调制函数

一般地，强度调制函数φ(t)应满足如下的条件：

φ(t)>0，max[φ(t)]=1

(14)

对于光滑连续的强度调制函数，上述条件可改写为：

φ′(t*)=0，φ″(t*)<0，φ(t*)=1

(15)

式中，t*为地震动加速度峰值的到达时刻。

SHINOZUKA[17]提出了一种光滑连续型的强度调制函数：

φ(t)=c[exp(-at)-exp(-bt)],

a,b,c>0，b>a

(16)

根据强度调制函数φ(t)所满足的条件式(15)，可得：

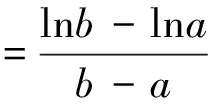
(17)

于是，式(16)也可写成二参数的形式：

b>a>0

(18)

对于强度调制函数式(18)，随着a,b值的增大，峰值达到时刻越早且衰减越快。下面，将式(18)的强度调制函数拓展到一类新的时-频调制函数中。

2.2 时-频调制函数

强度调制函数仅考虑了强度的非平稳，并未考虑频谱也是随时间变化的。事实上，地震动过程的非平稳性包括强度非平稳和频率非平稳两个方面，即地震动的强度和能量随频率的分布是非平稳的。因此，时-频调制函数更能全面地反映地震动的非平稳特性[18]。

在强度调制函数式(18)的基础上，建议的时-频调制函数为：

A(t,ω)=

ω>0,t>0

(19a)

其中

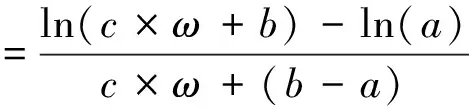
(19b)

在上述时-频调制函数A(t,ω)中，共有三个参数a、b、c，本文建议b=a+0.001，c=0.005。这样，只有一个独立的参数a，其值如表1所示。

表1 时-频调制函数的参数值

对于时-频调制函数式(19)，本文给出另一种改进的形式：

A(t,ω)=

ω>0,t>0

(20a)

其中

(20b)

式中，ωg是场地土的卓越圆频率；参数a,b,c与式(19)中的取值完全相同。

3 全非平稳地震动过程的实现

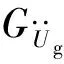
(21)

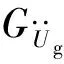
对于平稳过程的功率谱，本文采用Clough-Penzien谱[19]：

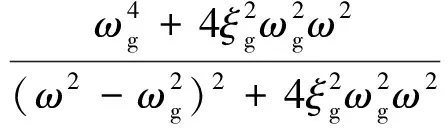
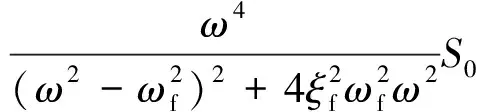
(22a)

其中

(22b)

式中，ωg和ξg分别为场地土的卓越圆频率和阻尼比；ωf和ξf分别为基岩的卓越圆频率和阻尼比，取ωf=0.1ωg，ξf=ξg；amax是地震动峰值加速度；r是峰值因子。

为了与我国现行的《建筑抗震设计规范》(GB 50011—2010)相一致，表2是卓越圆频率ωg和阻尼比ξg的取值，表3是地震动峰值加速度amax的取值，表4是峰值因子r的取值。

(2) Trypsinogen-1: Trypsin is a member of the serine protease family composed of three trypsinogen genes(trypsinogen 1, 2 and 4) with a potential role in cancer invasion[44,45]. These family members are sharing same nucleotide structures above 90% with each other.

表2 场地土的参数取值

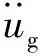
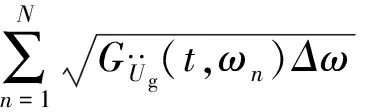
(23)

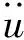
表3 地震动峰值加速度amax

注：括号内数值分别用于设计基本地震加速度为0.15g和0.30g的地区

表4 峰值因子r的取值

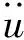
平均相对误差：

εm=

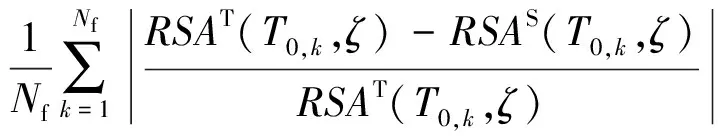
(24)

式中，T0,k是结构自振周期T0的第k个离散点值；Nf表示6 s内结构自振周期的离散点数，即Nf=6/ΔT0，ΔT0为结构自振周期的离散步长，一般取ΔT0=0.01 s；[εm]为容许的平均相对误差，一般取[εm]=5%。

最大相对误差：

εmax=

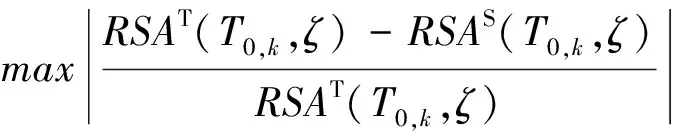
(25)

平均相对误差εm反映了平均反应谱RSAS(T0,ζ)与目标反应谱RSAT(T0,ζ)的整体拟合程度，最大相对误差εmax则反映了两者的局部拟合程度。

当上述两个相对误差不能满足时，需要对演变功率谱进行迭代修正：

k=0,1,…,K

(26)

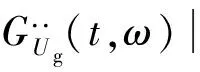
4 分析与验证

为了生成非平稳地震动过程的代表性时程集合。首先，需要选取基本随机变量Θ在区间[-π,π]上的代表性点：

θj=-π+2(j-0.5)π/nsel，

j=1,2,…,nsel

(27)

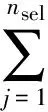
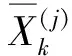
在式(23)中，截断项数N=1 600，频率间隔Δω=0.15 rad/s，截断频率ωu=240 rad/s，以式(20)所示的时-频调制函数来计算。在本文中，仅考虑设防地震烈度为8度，设计基本地震加速度为0.2g，根据现行的建筑抗震设计规范，地震动峰值加速度amax=200cm/s2，水平地震影响系数最大值αmax=0.45。同时，考虑设计地震分组为第二组，场地类别为I0、I1、Ⅱ、Ⅲ、Ⅳ的特征周期Tg分别为0.25 s、0.3 s、0.4 s、0.55 s和0.75 s。为生成非平稳地震动加速度过程的代表性时程，假定相应的地震动持时T分别为15 s、20 s、25 s、30 s、35 s，代表性时程的时间步长Δt=0.01 s。根据式(11)，非平稳地震动加速度过程的均方相对误差分别为ε(N)=1.9%、2.0%、1.7%、1.5%和1.3%，均小于5%的容许误差。

在迭代修正时，因计算平均反应谱的离散频率步长与生成地震动时程的离散频率步长不一致，一般需要进行插值。为避免插值带来的不便，在具体计算中，可先根据规范反应谱，将计算平均反应谱分成四段分别进行多项式最小二乘法拟合，这样，计算平均反应谱可表示为一个连续的分段多项式函数。从而，为迭代修正后生成地震动时程带来方便。

按照非平稳地震动过程的谱表示——随机函数方法，本文生成了nsel=144条的代表性时程。图1为非平稳地震动加速度过程的代表性时程，其中图1(a)为场地类别I1的代表性时程，图1(b)为场地类别Ⅲ的代表性时程，它们都具有非平稳地震动的典型特征。

图2为场地类别I1的演变功率谱，其中图2(a)为第0次迭代结果，图2(b)为第3次迭代结果。可见，对于场地类别I1，第3次迭代的演变功率谱的主要频率范围变小，而谱值变大，这表明地震动能量更加集中在一定的范围内。事实上，迭代后的演变功率谱的主要能量范围与规范反应谱有直接联系，随着场地类别的不同，地震动的主要能量范围可能变小或者变大。

图1 非平稳地震动过程的代表性时程Fig.1 Representation time-histories of non-stationary ground motion

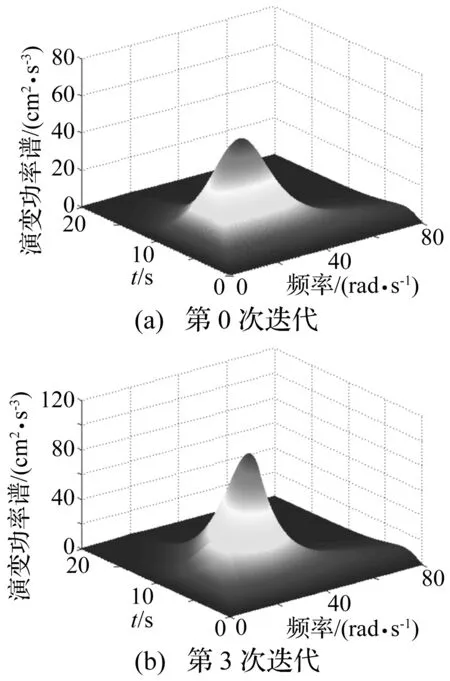
图2 场地类别I1的演变功率谱Fig.2 Evolutionary power spectra for site classification I1

图3给出了设计地震分组为第二组，场地类别分别为I0、I1、Ⅱ、Ⅲ、Ⅳ的地震加速度反应谱。 从图3可知，第0次迭代的结果与规范反应谱在长周期部分的差异较大，这是由于规范反应谱人为提高了长周期部分的谱值所致；而第3次迭代的结果则与规范反应谱的拟合程度十分理想，完全可以达到建筑抗震设计的要求。

表5给出了计算平均反应谱与规范反应谱的相对误差，除场地类别I0的最大相对误差稍大于容许误差外，第3次迭代的相对误差均在容许误差范围内。此外，从场地类别I0到Ⅳ，计算平均反应谱与规范反应谱的拟合误差越小。

表5 计算的相对误差

图3 地震加速度反应谱的比较Fig.3 Comparisons of earthquake acceleration response spectrum

5 结 论

本文面向现行的建筑抗震设计规范，建立了一类全非平稳地震动过程的概率模型，具体包括以下几个方面的研究进展：

(1)发展了一类具有时-频调制函数的演变功率谱模型，该模型概念清晰、理论完善，能够全面反映地震动的强度和频率非平稳特性，同时给出了与建筑抗震设计规范中场地类别及设计地震分组相对应的模型参数取值。

(2)采用了非平稳地震动过程模拟的谱表示-随机函数方法，该方法算法简单、结果可靠，生成的代表性时程具有数量可控、概率完备的特点，可从代表性时程集合的角度考察地震动过程。

(3)提出了基于演变功率谱的迭代算法和反应谱容许误差的双重控制方式，一般仅需对演变功率谱进行三次迭代修正，即可获得与建筑抗震设计规范反应谱一致性的结果。

(4)全非平稳地震动过程的概率模型具有计算效率高和拟合精度高的特点，且与概率密度演化方法具有天然的统一性，为应用结构随机动力学进行工程抗震设计提供了基础。

[1] 欧进萍, 牛荻涛, 杜修力. 设计用随机地震动的模型及其参数确定[J]. 地震工程与工程振动, 1991, 11(3): 45-54. OU Jinping, NIU Ditao, DU Xiuli. Random earthquake ground motion model and its parameter determination used in aseismic design [J]. Earthquake Engineering and Engineering Vibration, 1991, 11(3): 45-54.

[2] YEH C H, WEN Y K. Modeling of nonstationary ground motion and analysis of inelastic structural response [J]. Structural Safety, 1990, 8: 281-298.

[3] WANG J, FAN L, QIAN S, et al. Simulations of non-stationary frequency content and its importance to seismic assessment of structures [J]. Earthquake Engineering and Structural Dynamics, 2002, 31:993-1005.

[4] 刘章军, 王磊, 但庆文, 等. 非平稳地震动的广义演变谱模型及在水工抗震中的应用[J]. 水利学报, 2015, 46(9): 1028-1036. LIU Zhangjun, WANG Lei, DAN Qingwen, et al. Generalized evolutionary spectrum of non-stationary ground motion and its applications in seismic design of hydraulic structures [J]. Journal of Hydraulic Engineering, 2015, 46(9): 1028-1036.

[5] 杨庆山, 田玉基. 地震地面运动及其人工合成[M]. 北京: 科学出版社, 2014.

[6] 张郁山, 赵凤新. 基于小波函数的地震动反应谱拟合方法[J]. 土木工程学报, 2014, 47(1): 70-81. ZHANG Yushan, ZHAO Fengxin. Matching method of ground-motion response spectrum based on the wavelet function [J]. China Civil Engineering Journal, 2014, 47(1): 70-81.

[7] CACCIOLA P. A stochastic approach for generating spectrum compatible fully nonstationary earthquakes[J]. Computers and Structures, 2010, 88: 889-901.

[8] LI J, CHEN J B. Stochastic dynamics of structures [M]. Singapore: John Wiley & Sons Pte Ltd., 2009.

[9] 王鼎, 李杰. 工程地震动的物理随机函数模型[J]. 中国科学: 技术科学, 2011, 41(3): 356-364. WANG Ding, LI Jie. Physical random function model of ground motions for engineering purposes [J]. Science China Technological Sciences, 2011, 41(3): 356-364.

[10] 李杰, 王鼎. 工程随机地震动物理模型的参数统计与检验[J]. 地震工程与工程振动, 2013, 33(4): 81-88. LI Jie, WANG Ding. Parametric statistic and certification of physical stochastic model of seismic ground motion for engineering purposes [J]. Journal of Earthquake Engineering and Engineering Vibration, 2013, 33(4): 81-88.

[11] 刘章军, 曾波, 周宜红, 等. 地震动过程的概率模型及在重力坝抗震可靠度分析中的应用[J]. 水利学报, 2014, 45(9): 1066-1074. LIU Zhangjun, ZENG Bo, ZHOU Yihong, et al. Probabilistic model of ground motion processes and seismic dynamic reliability analysis of the gravity dam [J]. Journal of Hydraulic Engineering, 2014, 45(9): 1066-1074.

[12] 刘章军, 曾波, 吴林强. 非平稳地震动过程模拟的谱表示-随机函数方法[J]. 振动工程学报, 2015, 28(3): 411-417. LIU Zhangjun, ZENG Bo, WU Linqiang. Simulation of non-stationary ground motion by spectral representation and random functions [J]. Journal of Vibration Engineering, 2015, 28(3): 411-417.

[13] 建筑抗震设计规范:GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010.

[14] 薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10. XUE Suduo, WANG Xuesheng, CAO Zi. Parameters study on seismic random model based on the new seismic code [J]. China Civil Engineering Journal, 2003, 36(5): 5-10.

[15] LIU Zhangjun, LIU Wei, PENG Yongbo. Random function based spectral representation of stationary and non-stationary stochastic processes [J]. Probabilistic Engineering Mechanics, 2016,45:115-126.

[16] 刘章军, 方兴. 平稳地震动过程的随机函数-谱表示模拟[J]. 振动与冲击, 2013, 32(24): 6-10. LIU Zhangjun, FANG Xing. Simulation of stationary ground motion with random functions and spectral representation [J]. Journal of Vibration and Shock, 2013, 32(24): 6-10.

[17] SHINOZUKA M, SATO Y. Simulation of nonstationary random processes [J]. Journal of Engineering Mechanics Division, ASCE, 1967, 93(1): 11-40.

[18] DEODATIS G, SHINOZUKA M. Simulation of seismic ground motion using stochastic waves [J]. Journal of Engineering Mechanics, 1989, 115(12): 2723-2736.

[19] CLOUGH R W, PENZIEN J. Dynamics of Structures [M]. New York:McGraw-Hill, 1975.

Probability model of fully non-stationary ground motion with the target response spectrum compatible

LIU Zhangjun1,2, LIU Zenghui1, LIU Wei1

(1. College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China;2. Hubei Key Laboratory of Disaster Prevention and Reduction, China Three Gorges University, Yichang 443002, China)

Based on the intensity modulation function, a class of extended time-frequency modulation function for non-stationary ground motion was developed. In conjunction with the power spectral density function of stationary earthquake processes, an evolutionary power spectra model of fully non-stationary ground motion was established. The values of the model parameters were determined according to the Chinese code for seismic design of buildings. Applying the simulation method of hybrid spectral representation and random function for non-stationary stochastic processes, a complete set of representative seismic time-histories with assigned probabilities was obtained, and the average response spectrum of representative seismic time-histories was determined accordingly. In order to ensure the calculated average response spectrum to be in agreement with the design response spectrum, the average relative error and the maximum relative error were suggested to control the tolerance between the two response spectrums. The agreement was realized through three times iterative corrections for the evolutionary power spectra. The study provides a basis for the application of stochastic dynamics of structures in engineering practices.

earthquake ground motion; non-stationary processes; time-frequency modulation function; probability model; response spectrum; seismic design

国家自然科学基金资助项目(51278282;50808113)

2015-11-17 修改稿收到日期：2016-04-18

刘章军 男，博士，教授，博士生导师，1973年生

P315.9;TU311.3

A

10.13465/j.cnki.jvs.2017.02.005