基于动响应约束的结构材料优化设计

赵志军，荣见华，黄方林，岳海玲

(1.中南大学 土木工程学院，长沙 410075; 2.长沙理工大学 汽车与机械工程学院，长沙 410076;3.长沙学院 土木建筑工程系，长沙 410022;4. 长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室科研平台,长沙 410076)

基于动响应约束的结构材料优化设计

赵志军1,3,4，荣见华2，黄方林1，岳海玲4

(1.中南大学 土木工程学院，长沙 410075; 2.长沙理工大学 汽车与机械工程学院，长沙 410076;3.长沙学院 土木建筑工程系，长沙 410022;4. 长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室科研平台,长沙 410076)

针对于随机荷载作用下动响应为约束的结构材料优化问题，基于结构拓扑优化思想,提出了一种变动响应约束的结构材料优化方法。采用分式有理式和幂函数识别结构材料单元特性参数，以微观单元拓扑变量倒数为设计变量，导出了频率及振型对微观单元设计变量的一阶导数，进而得到了随机荷载作用下结构均方响应的一阶近似展开式。结合变约束限的思想，建立了以结构质量作为目标函数，均方响应作为约束条件的连续体微结构拓扑优化近似模型，并采用对偶方法进行求解。对典型结构进行了考虑单个和多个动响应约束的结构材料优化设计，优化所得结果验证了该方法的有效性和可行性。

微结构；拓扑优化；动响应约束；材料设计

由于有序多孔材料具有复杂大型的特点，结构离散完全计算的计算量巨大，等效连续介质分析方法是研究其静态弹性行为和动力学分析的有效途径[1-2]。基于小参数展开理论的数学均匀化方法将周期性多孔材料结构力学分析问题分解为一个微结构问题和一个宏观结构问题，并通过微结构的等效材料特性和特征位移(又称为影响函数)实现两尺度有限元分析的耦合。特征单元(eigenelement)法和基于高阶单元的serendipity 特征单元法也是一种求解周期性多孔材料等效特性的代表性方法。SIGMUND[3]提出了复合材料微结构单胞拓扑优化设计理论，现在已经成为材料研究的主要手段之一。HASSANI等[4-5]对均匀化理论进行了系统的阐述。基于周期性多孔材料等效连续介质分析方法的发展，结构材料优化设计方面已获得了一些研究进展[6-10]。NIU等[6]采用均匀化方法进行了结构最大自然频率的两种尺度拓扑优化设计。HUANG等[7]基于渐进结构优化方法(Evolutionary Structural Optimization,ESO)进行了结构最大刚度的结构材料设计。ZUO等[8]采用渐进优化方法实现了结构最大自然频率的多尺度拓扑优化设计。XU等[9-10]进行了考虑单点动响应要求的结构和材料一体化优化设计。尽管,在基于拓扑优化的材料设计方面已开展了大量工作, 但涉及结构动响应要求的材料设计工作相对有限，尤其是未见有考虑多点动响应约束情况下的结构材料优化设计。

本文借鉴均匀化方法，以微观单元拓扑变量倒数为设计变量，推导了随机荷载作用下结构均方响应的一阶近似显式展开式。结合变约束限的思想，得到了以结构质量作为目标函数，多点动响应作为约束条件的连续体微结构(即材料)拓扑优化近似模型，并采用对偶方法进行求解。给出的验证算例表明，本文方法可以进行多点动响应约束的结构材料优化设计。

1 微观尺度下的单元拓扑变量与过滤函数

假设宏观结构由微观周期性多孔结构组成。基于数学均匀化方法和代表体单元方法思想，宏观结构由宏观单元构成，而宏观单元作为一个微观结构(即材料)由微观单元构成。宏观结构和微观结构组成见图1。

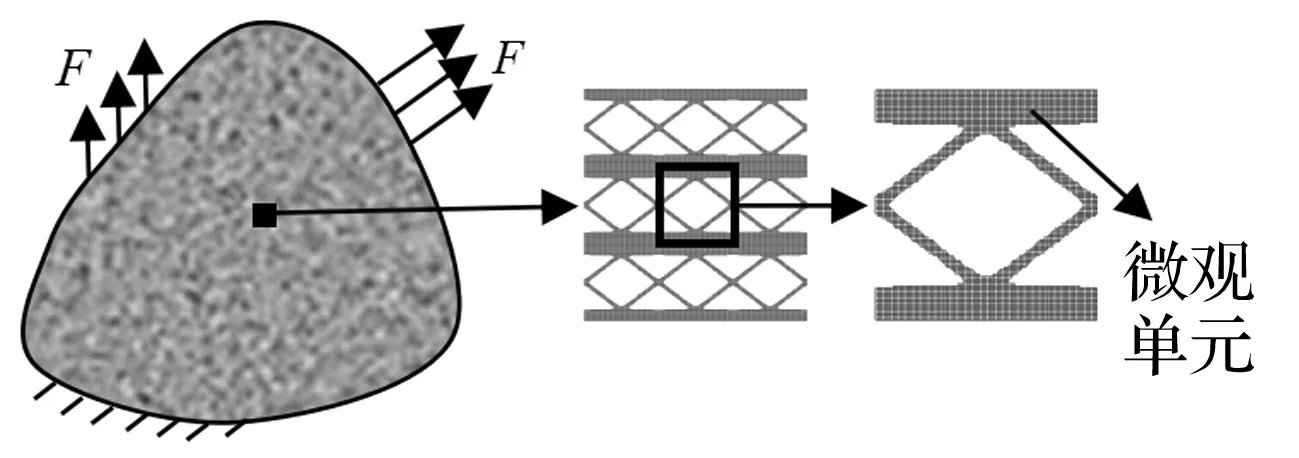
图1 宏观结构与微观结构Fig.1 Macrostructure and microstructure

微观结构的第s号微观单元的拓扑变量设为ts。用过滤函数fD(ts)识别第s号微观单元的弹性矩阵，用fm(ts)识别第s号微观单元的密度，单元材料特性参数识别采用公式

[Ds]=fD(ts)[D0]，ρs=fm(ts)ρ0

(1)

式中，[D0]为微观单元固有弹性矩阵，ρ0为微观单元固有材料密度，[Ds]为当前插值的微观单元材料弹性矩阵，ρs为当前插值的微观单元材料密度。密度和弹性矩阵的过滤函数分别采用式(2)有理式和幂指数函数形式。

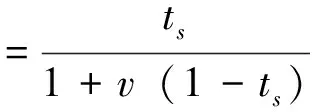
(2)

本文算例中取v=3.5，α=1.25，可以使单元质量与刚度比有界[11]，导致出现的局部模态频率为高频。从而有效地避免局部模态。

2 微观尺度下的结构动响应近似显式表示式

2.1 宏观结构总体刚度矩阵对微观单元设计变量的导数

宏观尺度下，第i号宏观单元刚度矩阵可以表示为

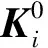
(3)

式中，Vi为第i号宏观单元的体积，[B]为该宏观单元的应变矩阵，[D]H为该宏观单元等效弹性矩阵，其表示式为

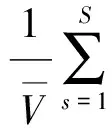
(4)

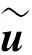
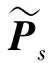
(5)

式中，[ε0]为给定初应变场，对于平面应力问题,{1,0,0}T，{0,1,0}T，{0,0,1}T为[ε0]的列向量。

为使函数展开式有更大的变量近似域[12]，本文取拓扑变量倒数为设计变量，即令xs=1/ts，等效弹性矩阵的导数可以表示为

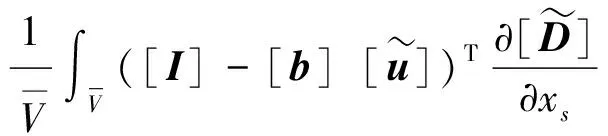
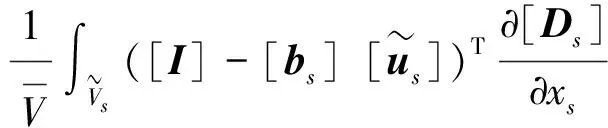
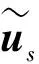
(6)

由式(3)及式(6)可以得到

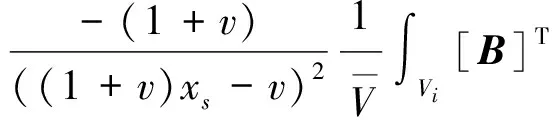
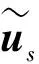
(7)

类似地,式(7)中的积分可以采用高斯形式表示。进而，宏观总体刚度矩阵对微观单元设计变量的导数可以表示为

(8)

2.2 宏观结构整体质量矩阵对微观单元设计变量的导数

宏观单元上任意点的单位体积上的惯性力可以表示为

(9)

{F}i=

(10)

宏观尺度下，该宏观单元等效质量矩阵可以表示为j

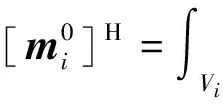
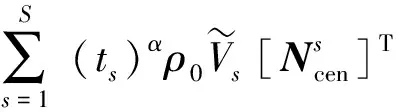
(11)

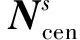
宏观单元等效质量矩阵的导数可以表示为

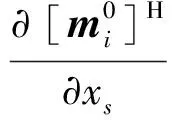
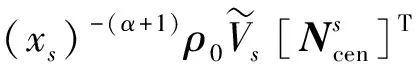
(12)

宏观整体质量矩阵对微观单元设计变量的导数可以表示为

(13)

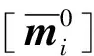
2.3 特征值对微观单元设计变量的导数

结构动力特性的特征值问题可用式(14a)和式(14b)表示

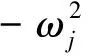
(14a)

{φj}T[M]{φj}=1

(14b)

式中，{φj}为第j阶质量正则化振型向量,ωj为结构第j阶固有频率值。对式(14a)求导可得

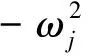
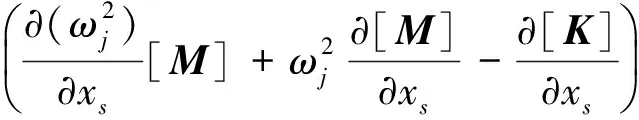
(15a)

方程两边同时左乘{φj}T，结合式(14a)，可得

(15b)

对式(14b)两边求导可得

(15c)

由式(8)、式(13)、式(15b)可得

Us,j+Vs,j

(16)

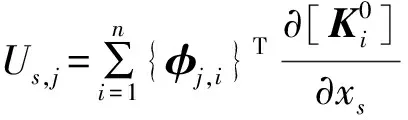
2.4 振形向量对微观单元设计变量的导数

设结构自由度总数为Nd，近似的取前nT(nT≪Nd)阶模态计算振型向量导数。可以假设振型向量导数表达式为

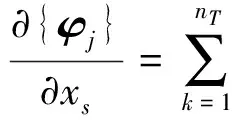
(17)

式中，βjk为待定系数。用{φk}T左乘式(15a),并将式(17)代入式(15a) 中，则有：

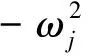
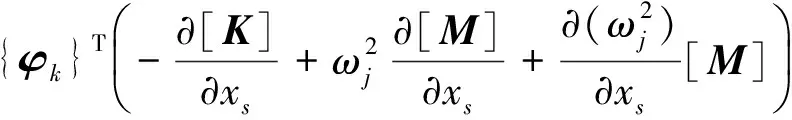
(18)

当k≠j时，由对称矩阵正交性可以简化式(18)，进而可得βjk的表达式为

(19)

当k=j时，将式(17)代入式(15c)，即可求出系数βjj为

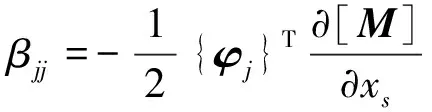
(20)

将式(8)、式(13)、式(19)、式(20)代入式(17), 就可以得到第j阶模态的特征向量的导数。

2.5 动响应的一般表示式

假设载荷矢量均值为零，自功率谱为[D]。为了简化计算，并求出结构上约束点的平均均方响应值，假设所描述系统的白噪声激励在所有自由度上互不相关，即有[D]=diag(Dq),(q=1,2,…,Nd)。参考文献[13]，结构动响应{y}的互协方差矩阵[Byryp]可表示为

[Byryp]=[Ryryp(0)]=[Φ] [Rqrqp(0)] [Φ]T

(21)

式中, [Φ]为结构振型矩阵。

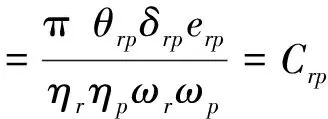
δrp=ζrωr+ζpωp，erp=Qrp-grp，

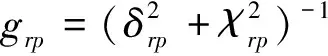
χrp=ηrωr+ηpωp，υrp=ηrωr-ηpωp，

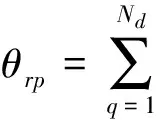
2.5.1 总体坐标系自由度方向的动响应

在树脂纯化过程中，常常需要通过泄漏曲线来确定所需树脂的量、上样体积和上样流速[33]。当流出液的浓度达到上样液浓度的1/10的时候，可以认为树脂的吸附量已达到饱和，此时的上样体积为最佳上样体积。从图3可以看出，树脂对花色苷的吸附效果随上样液体积的增加而下降，最佳上样体积达到183 mL。

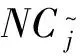
(1)情况一：[Φ]T[D] [Φ]=diag(θrr)

广义力不相关，自功率谱矩阵可以对角化，

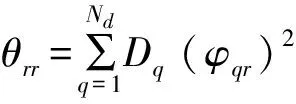
(22)

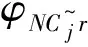
(2)情况二： [Φ]T[D] [Φ]=[θrp]

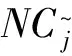
(23)

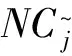
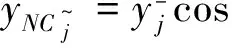
(24)

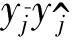
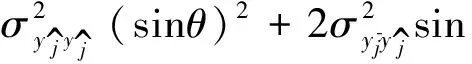
(25)

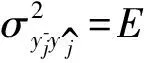
2.6 动响应对微观单元设计变量的导数

假设模态阻尼比ζr(r=1,2,…,nT)在优化迭代过程中不变。动响应对第s个设计变量的导数公式推导如下：

2.6.1 总体坐标系自由度方向动响应的导数

(1)广义力不相关情况下动响应的导数

根据式(22)的动响应表达式可得动响应导数为

(26)

(2) 广义力相关情况下动响应的导数

根据式(23)的动响应表达式可得动响应导数为：

(27)

式中,

(28)

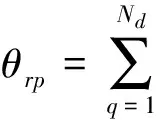
(29)

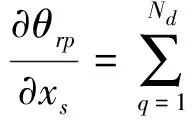
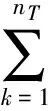
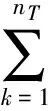
(30)

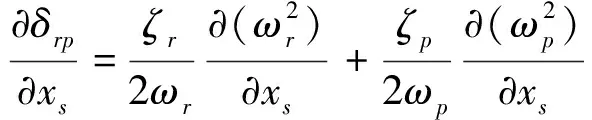
r,p=1,2,…,nT

(31)

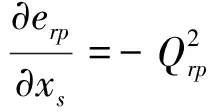
(32)

(33)

(34)

2.6.2 非总体坐标系自由度方向动响应的导数

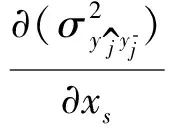
(35)

其中,

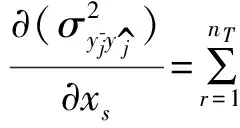
3 变动响应约束限的结构优化模型及求解

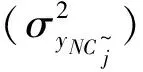
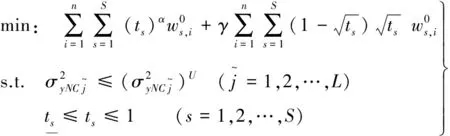
xs=1/ts(s=1,2,…,S)，类似于文献[14-16], 模型式(36)的求解转化为近似优化模型式(37)的求解。该近似模型中，目标函数用二阶泰勒级数近似展开并省略常数项，动响应约束函数用一阶近似式代替，进而得到以下近似模型：

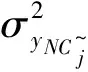
(38)

式中，β为动响应约束限变化因子，可在0.03～0.20间取值。αL为松弛系数，文中算例在1.01～1.05间取值。

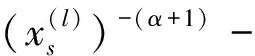
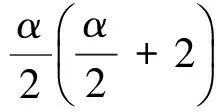
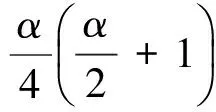
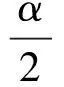
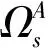
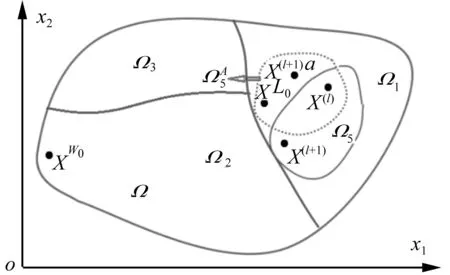
图2 优化迭代解示意图Fig.2 A simple representation of optimization iterative solutions

针对于微观结构优化问题，优化设计流程图见图3。

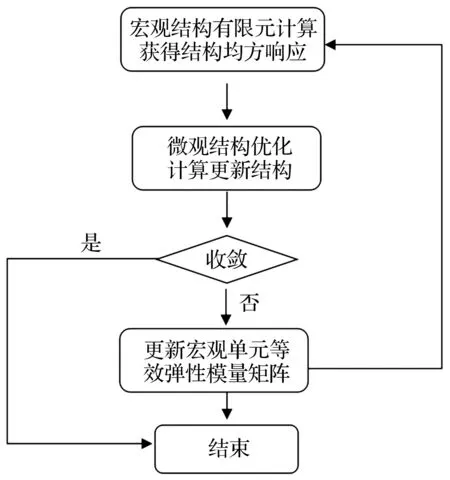
图3 优化流程图Fig.3 Flow chart of the optimization design

4 算例

4.1 算例一: 单点动响应要求的结构材料优化设计

图4所示结构是一平面应力悬臂梁。结构长0.5 m、宽0.2 m、厚度为0.002 m，悬臂端中点A作用有自功率谱DA=50 N2/Hz的竖直方向动载荷。材料固有弹性模量E=150 GPa，泊松比υ=0.3，固有材料密度ρ=8 000 kg/m3，各阶阻尼比相同，均为ζ=0.02。将宏观结构划分为50×20的有限元网格，微观结构(单胞)划分为100×100的有限元网格。

图4 悬臂梁宏观设计区域Fig.4 Design domain and loading case of a cantilever

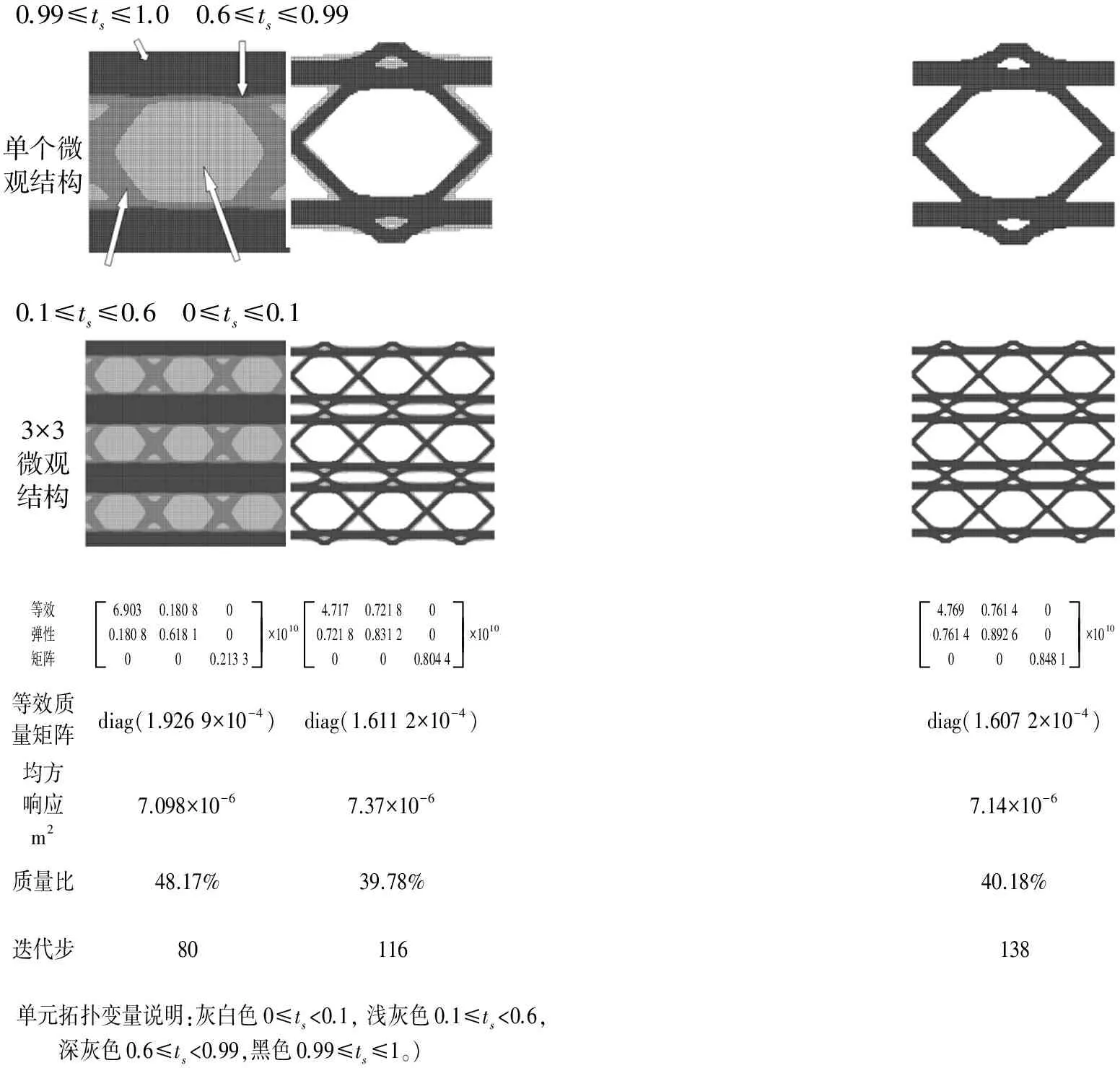
0．99≤ts≤1．0 0．6≤ts≤0．99单个微观结构0．1≤ts≤0．6 0≤ts≤0．13×3微观结构等效弹性矩阵 6．9030．180800．18080．61810000．2133éëêêùûúú×1010 4．7170．721800．72180．83120000．8044éëêêùûúú×10104．7690．761400．76140．89260000．8481éëêêùûúú×1010等效质量矩阵diag(1．9269×10-4)diag(1．6112×10-4)diag(1．6072×10-4)均方响应m27．098×10-67．37×10-67．14×10-6质量比48．17%39．78%40．18%迭代步80116138单元拓扑变量说明：灰白色0≤ts<0．1，浅灰色0．1≤ts<0．6，深灰色0．6≤ts<0．99，黑色0．99≤ts≤1。)

图5 悬臂梁微观结构优化历程

Fig.5 The optimization history of microstructure

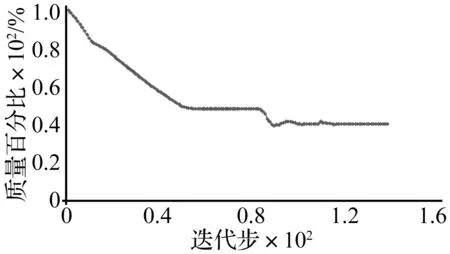
图6 悬臂梁结构质量历程Fig.6 The history of the mass of the optimized structure

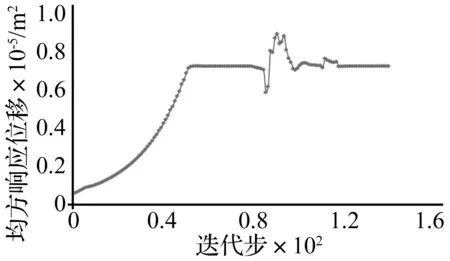
图7 A点处结构约束方向的均方响应历程Fig.7 The optimization history of the mean square dynamic response at the constraint point

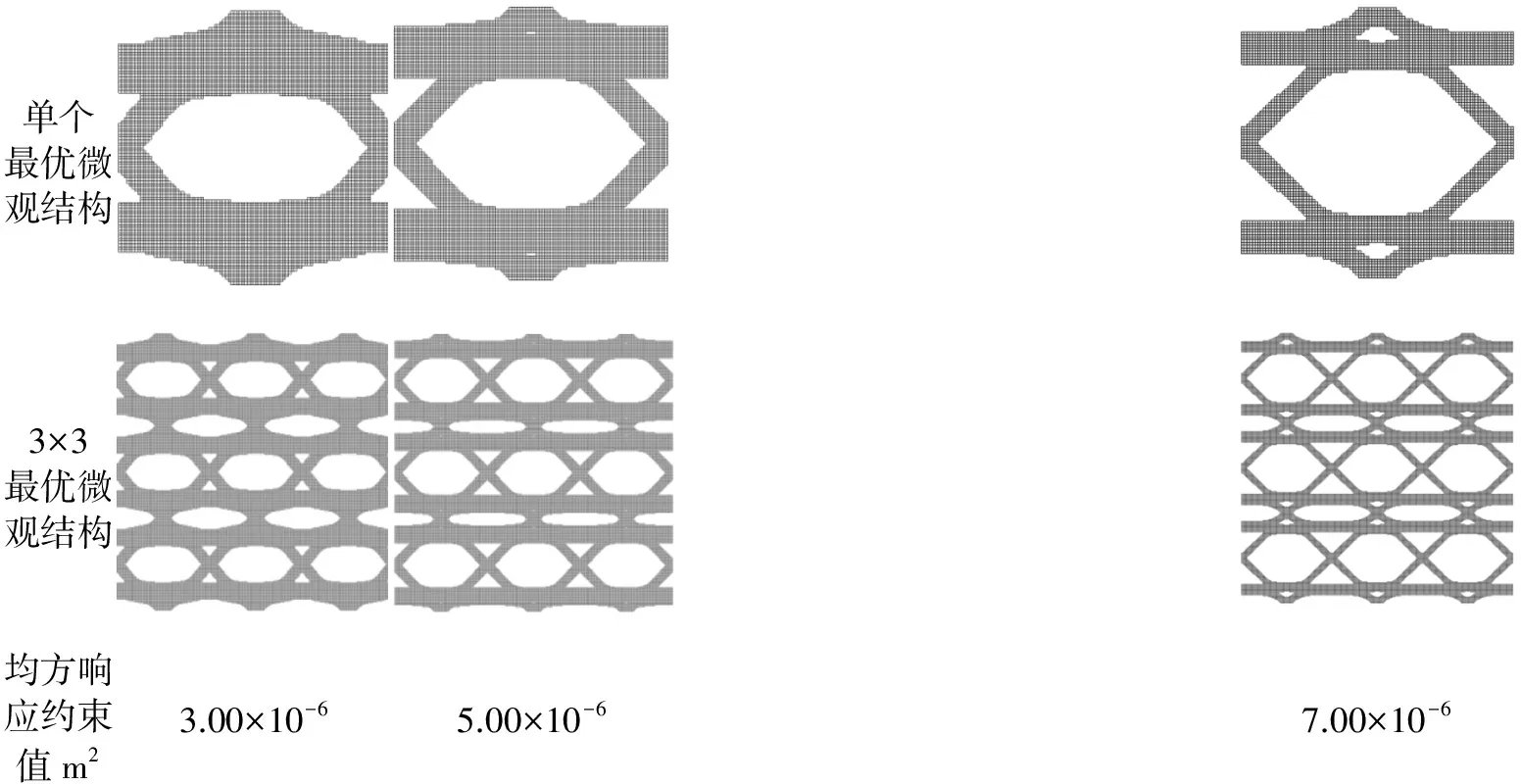
单个最优微观结构3×3最优微观结构均方响应约束值m23．00×10-65．00×10-67．00×10-6

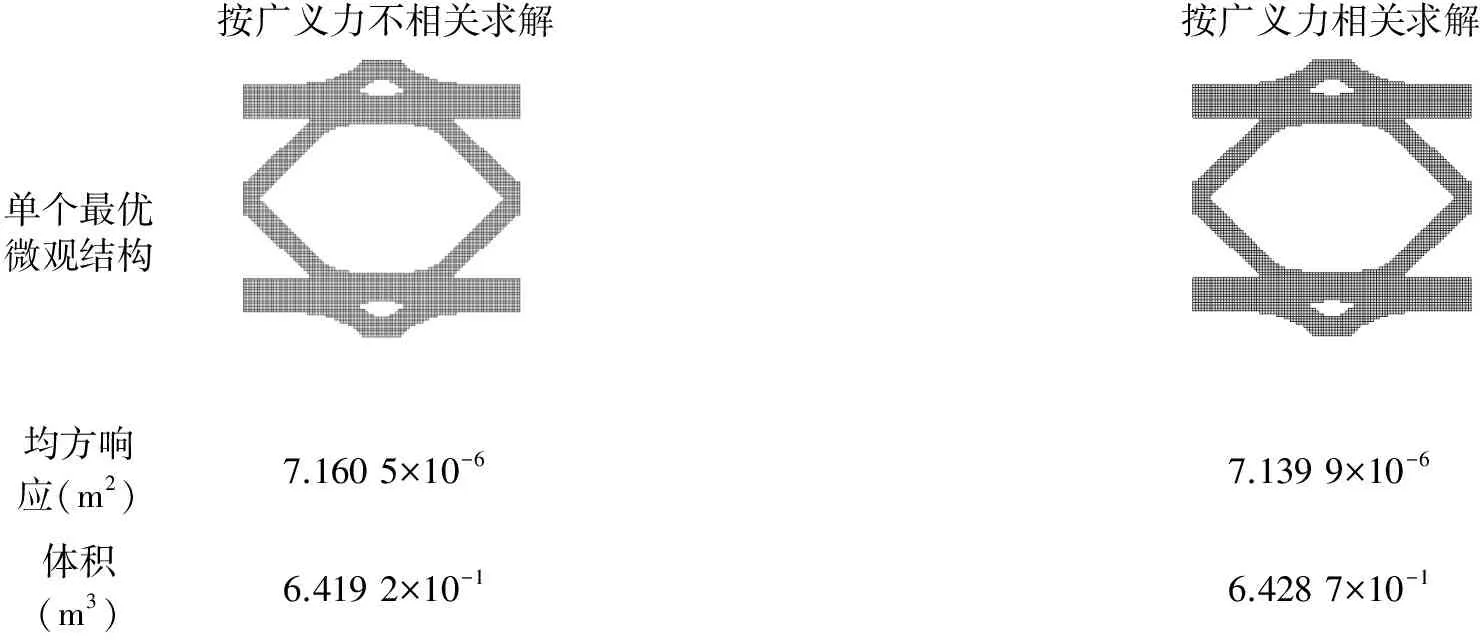
图8 不同均方响应约束下的最优微观结构

图9 按不同的情况(广义力相关或不相关)求解所得的最优微观结构

图10 动响应约束在同一点的不同方向上所获得的优化结果

Fig.10 The optimized micro structure with different direction constraint at the same point

4.2 算例二: 有多点动响应要求的结构材料优化设计

图11所示结构是一平面应力悬臂梁。结构长0.16 m、宽0.1 m、厚度为0.01 m。在A点竖直方向作用有自功率谱DA=40 N2/Hz的载荷。结构材料固有弹性模量E=210 GPa，泊松比υ=0.3，固有材料密度ρ=7 800 kg/m3，各阶阻尼比相同，均为ζ=0.02。宏观结构划分为64×40的有限元网格，将单胞划分为100×100的有限元网格。A点、B点和C点处竖直方向平均均方动响应上限值分别是2×10-7m2、8×10-8m2和8×10-8m2。本算例中，结构截断模态数nT为24，动响应约束限变化因子β=0.075，αL=1.03。微观结构优化进化历程如图12所示，结构总质量进化历程见图13，约束点处平均均方响应进化历程见图14。

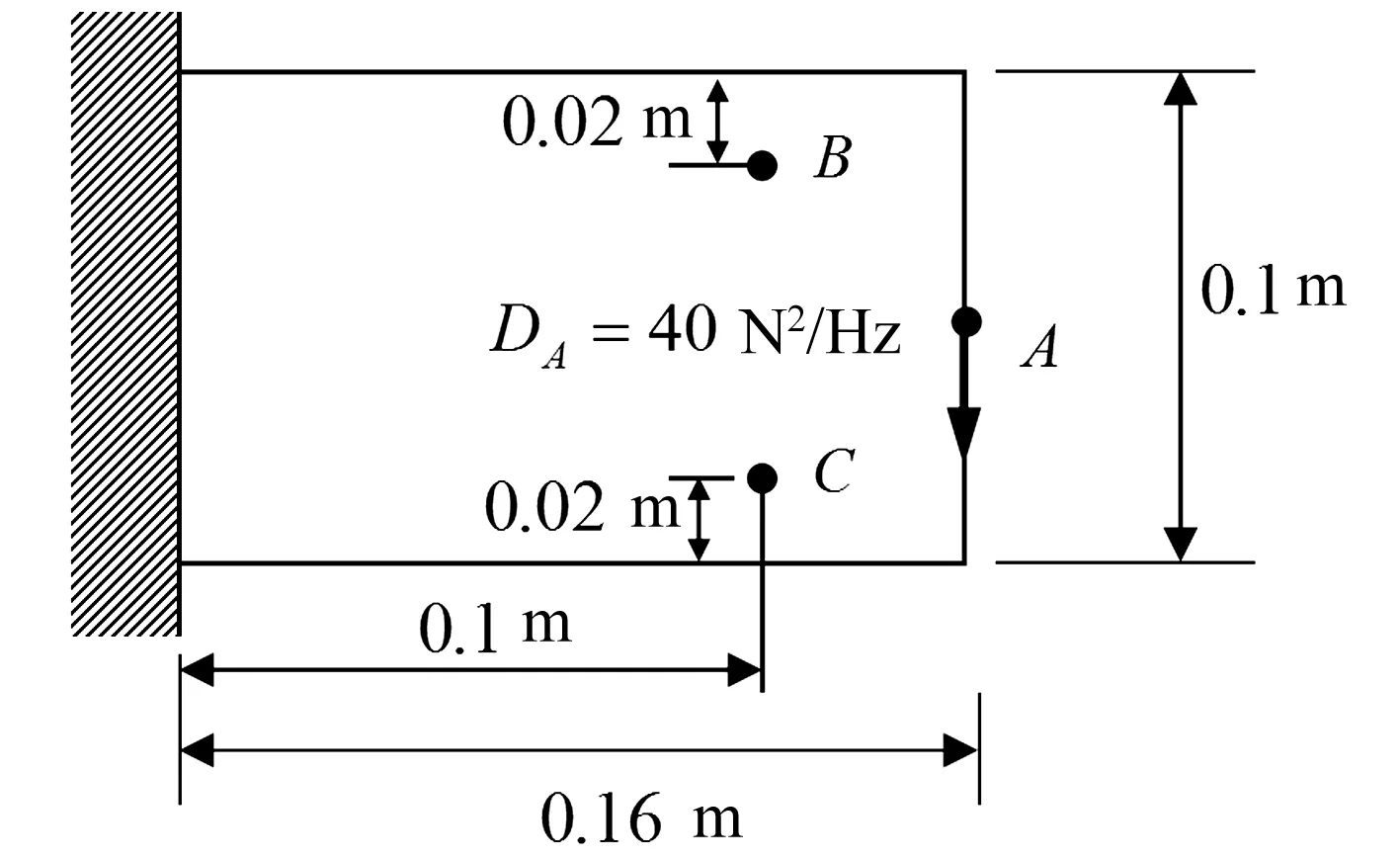
图11 多约束要求悬臂梁设计区域和载荷情况Fig.11 Design domain and loading case of a cantilever with multiple constraints

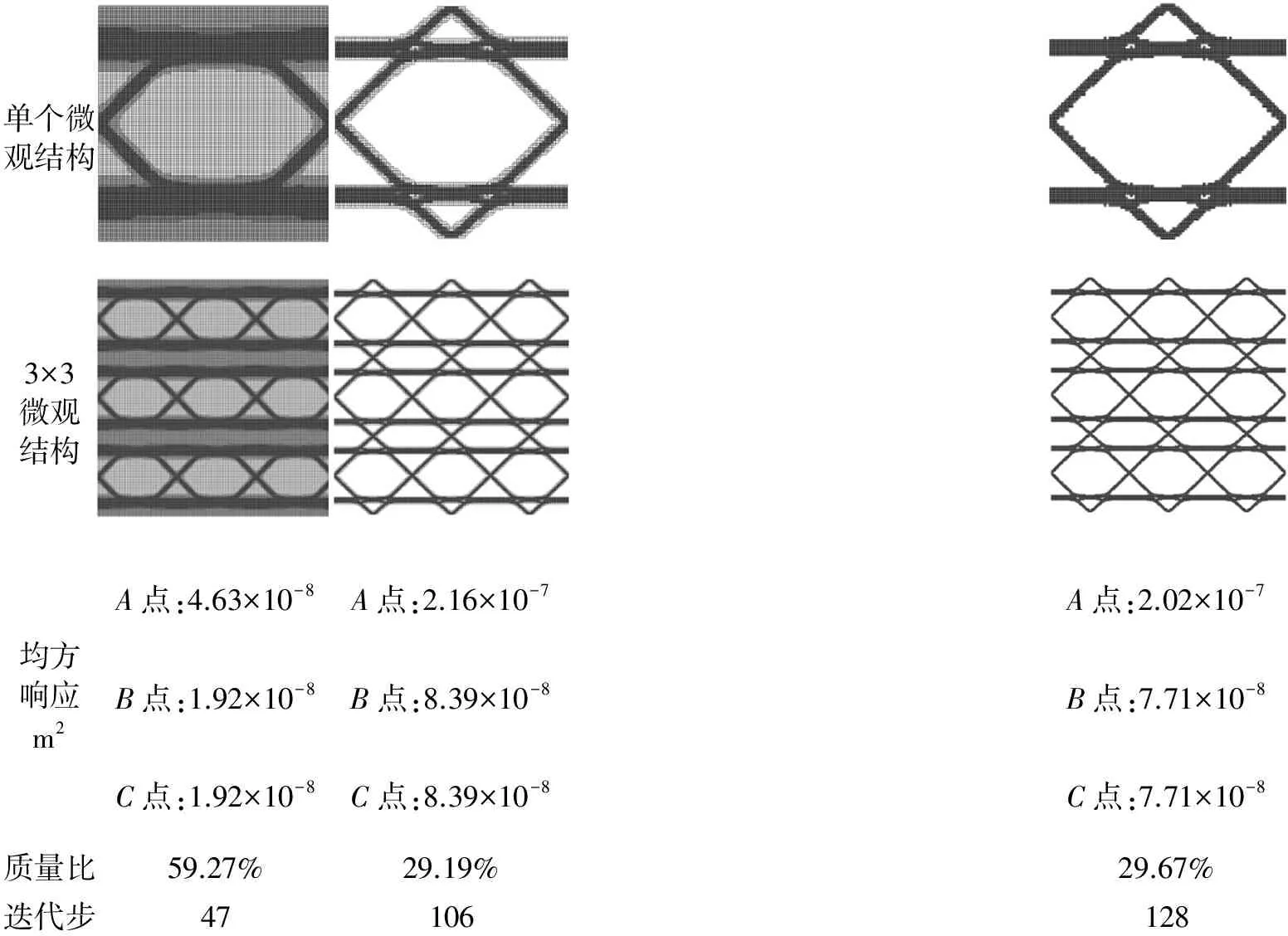
单个微观结构3×3微观结构A点：4．63×10-8A点：2．16×10-7A点：2．02×10-7均方响应m2B点：1．92×10-8B点：8．39×10-8B点：7．71×10-8C点：1．92×10-8C点：8．39×10-8C点：7．71×10-8质量比59．27%29．19%29．67%迭代步47106128

图12 多约束要求的悬臂梁微观结构优化历程

Fig.12 The optimization history of microstructure with multiple constraints

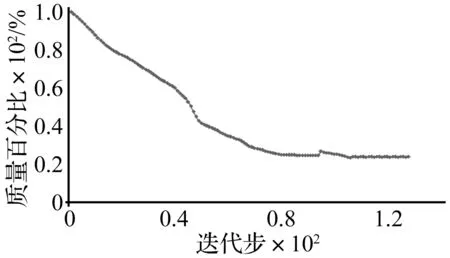
图13 多约束要求的悬臂梁结构质量历程Fig.13 The history of the mass of the optimized structure with multiple constraints

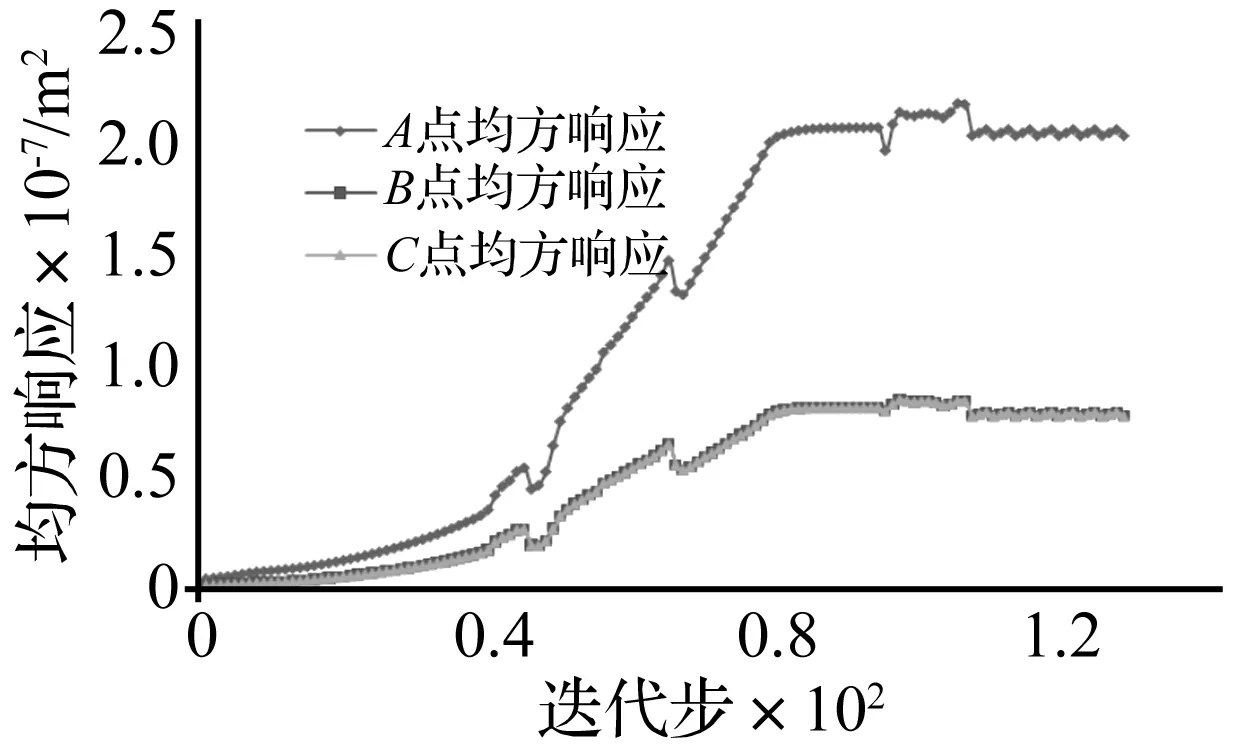
图14 多约束要求的悬臂梁结构约束点处均方响应历程Fig.14 The optimization history of the mean square dynamic response at the constraint points

5 结 论

针对于随机荷载作用下的拓扑优化问题，提出了一种基于动响应约束的连续体微观结构拓扑优化方法。给出两个算例。能够得出下列结论:

(1)提出的方法能有效地优化设计考虑随机荷载作用下单个及多个平均均方响应约束问题的连续体微观结构;

(2)在均方响应近似式中,考虑宏观单元等效质量矩阵的一阶量的影响,使得优化近似模型更有效;

(3)优化过程中获得的微观结构拓扑构型清晰。

[1] NETO M A, YU W B, TANG T, et al. Analysis and optimization of heterogeneous materials using the variational asymptotic method for unit cell homogenization[J]. Composite Structures,2010,92(12):2946-2954.

[2] XING Y F, YANG Y. An eigenelement method of periodical composite structures[J]. Composite Structures,2011, 93(2): 502-512.

[3] SIGMUND O. Materials with prescribed constitutive parameters：an inverse homogenization probiem[J]. Internationai Journal of Soiids and Structures,1994,31(17):2313-2329.

[4] HASSANI B, HINTON E. A review of homogenization and topology optimization Ⅰ—homogenization theory for media with periodic structure[J]. Computers & Structures,1998, 69(6):707-717.

[5] HASSANI B, HINTON E. A review of homogenization and topology optimization Ⅱ—analytical and numerical solution of homogenization equations[J]. Computers & Structures,1998, 69(6):719-738.

[6] NIU B, YAN J, CHENG G. Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency[J]. Structural Multidisciplinary Optimization, 2009, 39(2): 115-132.

[7] HUANG X, ZHOU S W, XIE Y M, et al. Topology optimization of microstructures of cellular materials and composites for macrostructures[J].Computational Materials Science, 2013, 67: 397-407.

[8] ZUO Zhihao, HUANG Xiaodong, RONG Jianhua, et al. Multi-scale design of composite materials and structures for maximum natural frequencies[J].Materials and Design, 2013,51: 1023-1034.

[9] XU B，XIE Y M. Concurrent design of composite macrostructure and cellular microstructure under random excitations[J]. Composite Structures, 2015, 123:65-77.

[10] YI Y M, PARK S H, YOUN S K. Design of microstructures of viscoelastic composites for optimal damping characteristics[J].International Journal of Solids and Structures,2000, 37(35): 4791-4810.

[11] 朱继宏, 张卫红, 邱克鹏.结构动力学拓扑优化局部模态现象分析[J]. 航空学报，2005, 126 (14):619-623. ZHU Jihong, ZHANG Weihong, QIU Kepeng, Investigation of localized modes in topology optimization of dynamic structures[J]. Acta Aeronautica et Astronautica Sinica,2005, 126 (14):619-623.

[12] ETMAN L F P, GROENWOLD A A,ROODA J E. First-order sequential convex programming using approximate diagonal QP subproblems[J]. Structural and Multidisciplinary Optimization, 2012, 45:479-488.

[13] RONG J H，XIE Y M, YANG X Y, et al. Topology optimization of structures under dynamic response constraints[J].Journal of Sound and Vibration,2000, 234(2): 177-189.

[14] 邢晓娟,荣见华,邓果.一种变频率约束限的结构拓扑优化方法[J]. 振动与冲击,2008,27(10):56-60. XING Xiaojuan, RONG Jianhua, DENG Guo. A structural topologic optimization method based on varying frequency constraint limits[J]. Journal of Vibration and Shock,2008,27(10):56-60.

[15] RONG J H, LIU X H, YI J J.An efficient structural topological optimization method for continuum structures with multiple displacement constraints[J].International Journal of Finite Elements in Analysis and Design,2011,47(8):913-921.

[16] RONG J H，YI J H.A structural topological optimization method for multi-displacement constraint problems and any initial topology configuration[J].International Journal of Acta Mechanica Sinica,2010,26(5): 735-744.

Topology optimization of micro structures with random vibration responses constraints

ZHAO Zhijun1,3,4, RONG Jianhua2, HUANG Fanglin1, YUE Hailing4

(1. School of Civil Engineering, Central South University, Changsha 410075, China；2. School of Automotive and Mechanical Engineering, Changsha University of Science and Technology, Changsha 410076, China；3. Department of Civil Engineering, Changsha University, Changsha 410022, China;4. Key Laboratory for Safety Control of Bridge Engineering,Changsha University of Science & Technology, Changsha 410076, China)

A structural material optimization method with varied random dynamic responses constraints was proposed to solve the problem of structural material optimization under random excitations, based on the structural topology optimization technology. By using the conventional rational approximation and power interpolation for material properties and masses and selecting the reciprocals of topological variables of micro structural elements as design variables, the first order derivatives of frequency and modal shape with respect to the design variables were derived. And the one order approximate explicit functions of dynamic responses were further achieved. Integrated with the idea of varied constraints, a topological optimization model of micro structures was built by taking the structural mass as the objective function and the dynamic responses as constraint functions. Then, a dual solving method was introduced. Several numerical examples were presented to verify the proposed optimization algorithm and the microstructures of cellular materials were obtained.

micro structure; topology optimization; random dynamic responses constraints; material design

国家自然科学基金项目(11372055);湖南省教育厅科学研究项目(15C0119;14C0098);长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金项目(13KB07)

2016-01-08 修改稿收到日期：2016-05-20

赵志军 男，博士生，讲师，1982年2月生

荣见华 男，博士,教授，1963年7月生 E-mail:rongjhua@aliyun.com

TU311.3；TB123

A

10.13465/j.cnki.jvs.2017.02.035