基于声发射及小波奇异性的钢轨损伤检测

宋 阳， 吴 凡， 刘德扣， 刘晓舟， 倪一清

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240； 2.香港理工大学 深圳研究院,智能结构健康监测研发中心，深圳 518057)

基于声发射及小波奇异性的钢轨损伤检测

宋 阳1， 吴 凡1， 刘德扣1， 刘晓舟2， 倪一清2

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240； 2.香港理工大学 深圳研究院,智能结构健康监测研发中心，深圳 518057)

很多重大脱轨事件都与钢轨的损伤密切相关，因此，对在役钢轨进行定期损伤检测显得尤为重要。研究首先运用声发射原理，通过对在役钢轨损伤前后监测系统所采集的数据信号进行时域及频域的分析，根据有损信号的能量谱特点，判断钢轨中损伤的存在。其次，运用小波奇异性检测原理探讨研究了定位损伤。通过分析各种连续小波变换算法的结果，得出à Trous算法在奇异性检测中能够较准确判断出奇异点位置。因此，结合声发射原理和小波处理的方法的无损监测可应用于在役钢轨的损伤检测和定位，对铁路钢轨损伤进行检测和预报。

钢轨；无损监测；声发射检测；小波奇异性分析

钢轨在使用过程中会因为制动摩擦、滚动荷载和残余应力等影响产生一系列损伤，比如磨损，塑性变形和疲劳损伤等，给铁路正常运行带来隐患。如何能够在损伤带来危害前无损且高效实时地检测钢轨健康状态，是如今钢轨探伤领域研究的新方向。常用的钢轨无损检测以传统压电超声检测技术为主，近些年发展的新技术包括：漏磁检测技术[1]，交变电场检测技术[2]，涡流检测技术[3]，电磁超声技术[4]，超声导波[5]及激光超声技术[6]等。

本研究运用的钢轨无损检测方法基于声发射(AE—Acoustic Emission)技术。这是一种被动无损检测技术，其原理基于材料局部因能量的快速释放而发出瞬态弹性波，在存在损伤时在特殊的频段会发出较高能量的弹性波[7]。声发射技术具有很高的灵敏度，可用于动态、连续和在线的无损监测，对滚动元件接触疲劳失效检测和寿命预测具有独特的优势[8]，近年一些学者在理论研究方面做出了很多突破。HESSE等[9]进行了关于面波在钢轨中传播的实验，研究了在不同频率下不同模型的钢轨中面波的传播速度，得出面波在钢轨中的频散曲线；CHONG等[10]研究了导波在钢轨中的传播损伤信号的特性，通过分析损伤信号来判断伤损位置；COCCIA等[11]进行了导波用于测量轨头损伤的数值模拟以及实验分析。

同时本研究还运用基于小波分析的奇异性检测手段对试验结果进行分析处理。小波分析的奇异性检测方法有：连续小波变换，模极大值法，基于多分辨率分析的正交小波变换快速算法(Mallat算法)和基于离散二进小波变换原理的快速算法(à Trous算法)等等。已有很多成功运用该方法于机械结构探伤的例子，如何浩祥等[12]利用小波变换奇异性检测中的模极大值法对网壳中的损伤进行判别和定位；杜守军等[13]根据小波奇异性加测理论，以应变能力的损伤信号作为结构损伤指标，对悬臂梁结构和平面桁架结构进行数值模拟并进行损伤定位；任青文等[14]以悬臂梁为例，利用数值模拟和实验分析的方法，通过模极大值的方法提出能够对损伤定位的指标，并讨论了该指标与损伤程度的关系。

本文通过对在役钢轨损伤前后监测系统所采集的数据信号进行时域和频域的分析，根据声发射原理和能量频谱法，得出钢轨有损判据；根据奇异性检测原理，通过比较连续小波变换、模极大值法以及à Trous算法三种方法对实验数据处理的结果，找出可行的小波判据判断损伤位置。

1 探伤原理简介

1.1 声发射探伤原理

1.2 小波奇异性探伤定位原理

小波变换具有空间局部性，它能“聚焦”空间的局部结构以确定信号的奇异性位置。同时小波变换不仅可以确定奇异发生的时间，而且可以进一步判断奇异的性质。奇异性检测主要思想是寻找小波变换中模极大值在细尺度下收敛的坐标以确定奇异发生的时间；通过小波变换模极大值的衰减计算Lipschitz指数，以判断奇异的性质。

用小波变换进行奇异性检测的方法有很多，比如连续小波变换(CWT)，因二进小波变换未对时间平移参数离散化而具有时间平移不变性，也适用于做奇异性检测；而离散二进小波变换可以通过à Trous算法快速实现，它类似于双正交小波中的Mallat算法。这些方法对于处理本文的有损数据都有其优缺点：利用连续小波变换处理信号，存在信息冗余，而且对较小的损伤，该方法不能明显的表现其奇异性；利用模极大值法处理信号，在收敛过程中，模极大线有可能中断，在某些尺度下奇异点附近没有模极大，而且模极大的点也不一定是奇异点，需要对Lipschitz指数计算进行进一步判断；利用à Trous算法处理信号，不需要对每一级系数进行抽取和插值，不受双正交条件的制约，而且选取的小波函数只需要满足二进小波条件即可，同时à Trous算法具备平移时不变性的特征，它只是对滤波器组进行内插补零，其每级分解系数和原时间序列的长度保持一致，是真正意义上的无抽取离散小波变换。

2 实测数据信号采集

信号采集系统为基于PZT传感器的铁路道岔探伤系统。火车或货车经过时，该套探伤系统被激发用来收集声发射信号检测道岔处是否存在裂缝。该系统应用声发射检测方法(AE)，利用过往列车作为激发荷载，传感器根据外部载荷产生响应信号。如果在道岔中有损伤，信号超过阈值，相应数据通过数据采集系统由电缆传送到附近控制室中的中央分析系统。阈值设定与无损状态信号的均方根有关。数据采集系统使用四通道的商业数据采集卡NI9223，采样率最高可达10 MHz；系统采用Labview 软件进行数据收集和分析。该探伤系统于2013年2月安装在使用中的钢轨道岔上。

传感器布置如图1所示，四片PZT传感器对称布置在两条钢轨内侧，分别距离道岔3.9 m和3.3 m。系统四个通道全部用来数据采集，通道1和3分别采集离道岔口3.9 m的两个传感器的信号；通道2和4分别采集离道岔口3.3 m的两个传感器的信号；采样率为600 kHz～1 MHz。在同年6月监测系统被警告信号激发并成功记录了损伤钢轨道岔的相关数据，在现场检查后看部分道岔轨头已经完全磨损掉落(图2)。

图1 传感器的分布 图2 钢轨道岔损伤Fig.1 Sensor arrangement Fig.2 Damage in rails

3 损伤识别

在道岔上安装探伤系统后，首先记录了时域基线信号视为无损信号，以用于损伤判断。在损伤发生后，对各个通道的信号进行了分析， 发现传感器1得到的无损数据信号和有损数据信号的差别较为明显，其波形图如图3(a)和(b)所示。 由两图对比可以看出，在同样时间段内，有损数据波形图3(b)中AE高频脉冲信号比无损数据波形图中3(a) 明显增多，即有损数据计数率或计数总和均高于无损数据，这是由于钢轨损伤破坏后在损伤处微裂缝反复发生变形产生AE高频弹性波。

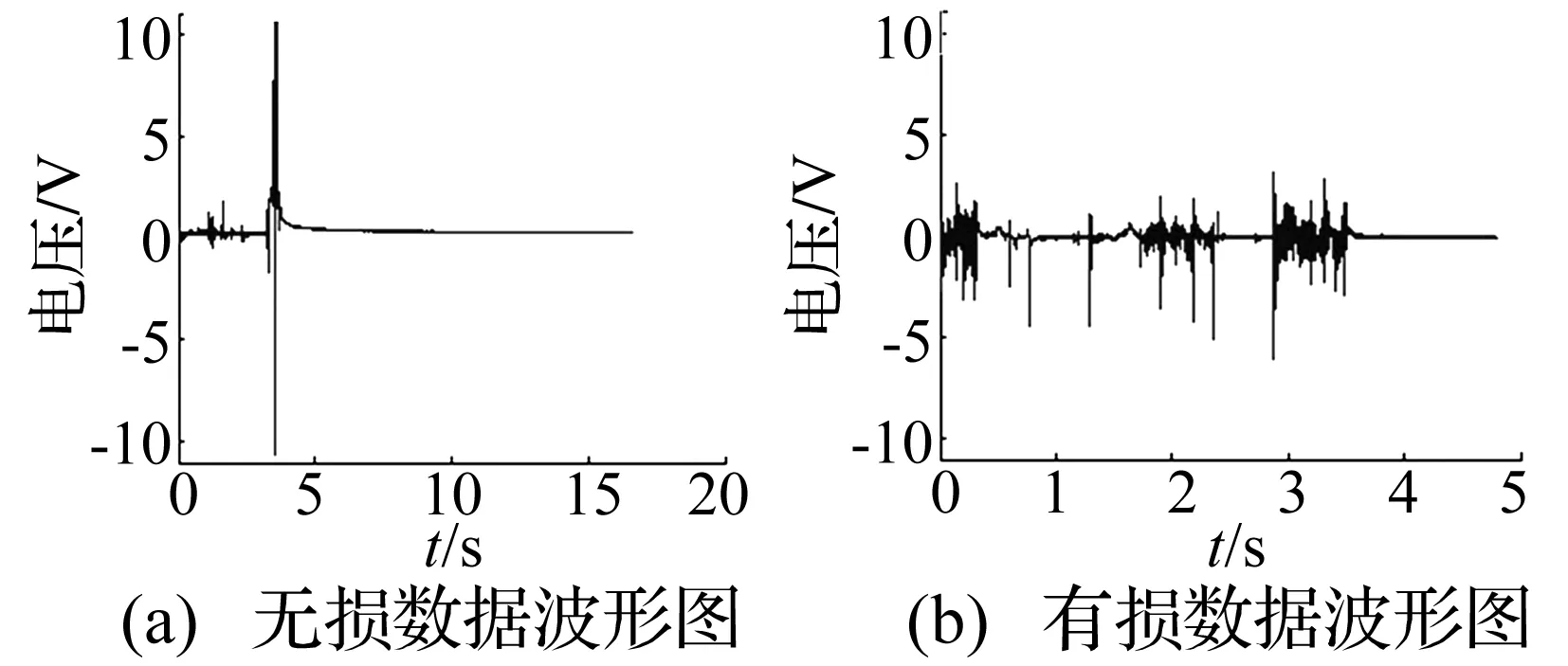
图3 传感器1信号波形图Fig.3 Waveform of sensor 1

用能量法如功率谱法通常能更好地表征结构的破坏。这里，我们将传感器1接收到的数据信号进行功率谱分析，得到对应的功率谱密度(PSD)图，传感器1无损、有损数据信号的功率谱密度曲线对比图如图4所示。

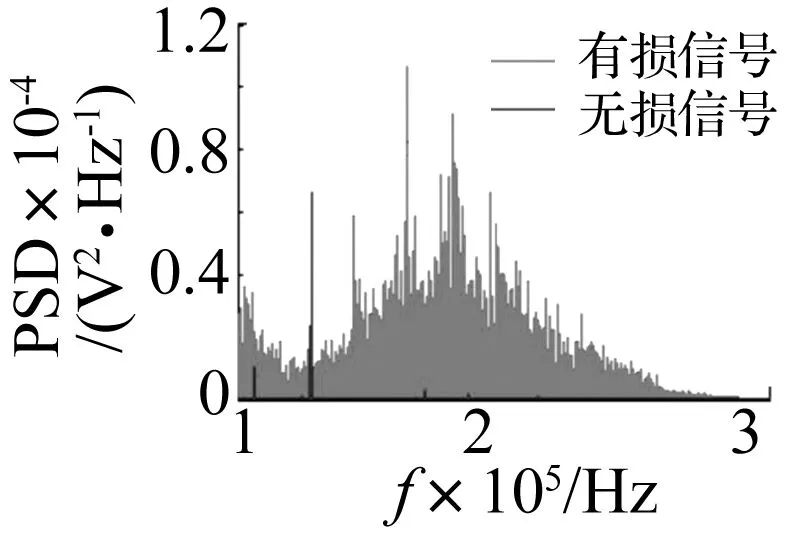
图4 传感器1有损、无损数据功率谱密度曲线对比Fig.4 PSD of data with and without damage of sensor 1

从图4有损、无损数据的功率谱曲线中，可以看出有损数据信号比无损数据信号具有更高的能量值，同时在100～300 kHz的频率范围内，有损数据信号出现了明显的能量峰值，这证实了先前的理论假设，即结构有损后会在特殊的高频段(100～300 kHz)产生高能AE弹性波。由此，通过分析现场探伤系统得到的数据，我们可以用AE瞬时脉冲和高频PSD成像特点判别出铁路轨道是否有破坏。

1.1 威斯康星卡片分类测试(Wisconsin card sorting test，WCST) WCST由Grant和Berg[6]编制，是一种较为常用的客观的执行能力测验方法之一。测试分别将128张颜色、形状及数目均不同的卡片多次呈现在患者的眼前，根据指示分类连续10次无误则完成测试，通过完成的分类数和持续性错误数来评分。该测验可客观、全面、综合地反映被试者的执行能力、思维组织能力以及抗干扰能力[7]。

4 损伤定位

4.1 奇异性检测结果

利用连续小波变换(CWT)，模极大值法和à Trous算法，对得到的损伤数据进行奇异性检测，使用连续小波变换时，连续小波变换系数小，由于存在的损伤较小，不能在CWT灰度图中明显表示，无法进行奇异性的判断；使用模极大值算法时，原始信号处理后存在较多的奇异点，给准确判断出实际损伤的位置带来很大的困难。图5与图6分别显示用CWT和模极大值处理有损数据时的困难程度。相比以上两种算法，基于离散二进小波变换原理的à Trous算法，不会存在信息丢失等问题，可以保证奇异性检测的准确性。

图5 连续小波变换数据处理Fig.5 Data processed by CWT

图6 模极大值法数据处理Fig.6 Data processed by Mallat algorithm

将传感器1和2得到的有损数据原信号及该信号分解后各频段信号数据，进行à Trous算法检测奇异性，可得到对应的变换系数图，其中传感器1变换系数图如图7所示。

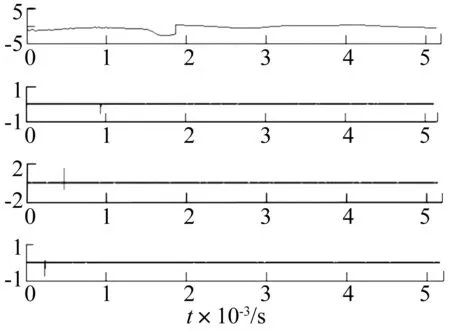
图7 传感器1有损数据原信号及cd1、cd2和cd3各频段信号二进小波变换系数Fig.7 Dyadic wavelet transform coefficients of the original data and the frequency band data of cd1， cd2 and cd3 from sensor 1

由图7可以发现，原信号进行各个频段处理后，表现为较明显的奇异性显示，可以基本判断奇异点的位置；高频段cd1、cd2和cd3的奇异性同样明显，可以准确判断出奇异点的时间位置，经过计算即可获得损伤存在的位置。同样地，在传感器2高频段的变换系数图中也发现了明显的奇异点。

4.2 位置判断

根据à Trous算法已经给出的奇异性处理结果，在图像中可以捕捉到奇异点的时间信息，如表1所示。

表1 à Trous 算法对有损数据处理得到奇异点的时间位置

根据离散小波变换得到各频段信号与原信号的之间的关系，及列车轮间距的存在对信号的触发产生的延迟效应，实际损伤发生时间计算公式为：

T=2n×Tn-L/V

(1)

式中 ：n为各频段对应的级数，Tn为各频段对应奇异点的时间位置，L为列车每组车轮中车轮间距，取值为0.6 m，V为应力波群速度，根据在PSD图谱分析中可以发现，波的频率在150～200 kHz之间，可以看到明显的能量峰值，同时，对应于参考文献[9]中关于频率与群速度的频散曲线图可以发现，在WS2(有损面波2)模型中，150～200 kHz的频率对应的群速度为2 840～2 900 m/s之间，本文中取2 850 m/s。根据上述时间计算公式，可以得到损伤发生的计算距离，和实际测量得到的损伤距离3.9 m和3.3 m进行比较可以得到误差，具体结果如表2所示。

表2 à Trous 算法对有损数据处理得到计算距离和其误差

从表2中可以看出，原始信号以及在不同频段处理得到的数据差异较小，意味着在不同频段得到的时间信息具有可靠性。在原始信号以及在不同的频段下，3.9 m处的传感器1损伤位置判断误差较大，3.3 m处的传感器2损伤位置判断误差较小。除了系统不可消除的误差存在之外，实测数据的采集系统、试验数据的提供以及实验数据处理方法都会给最终结果带来误差: 数据监测系统本身存在着取点误差；数据处理方法上存在理论误差，信号分解会造成一定的时间偏移，再经过时间还原，会给损伤定位带来一定的距离计算误差。

5 结 论

(1)通过数据时域图的比较，针对钢轨轨头剥落损伤，有损数据相比无损数据有更多的AE脉冲信号，即更多的幅值突变，这些聚集的AE脉冲信号与结构中损伤的形成和发展有关，从声发射事件计数角度，有损数据的计数率以及计数总和均高于无损数据，因此可以根据这种特点来判断损伤的存在。通过数据功率谱图的比较，也可以看出有损数据相比无损数据存在更明显的能量聚集，在100～300 kHz之间存在明显的能量突变，因此也可以根据这种特点判断损伤的存在，以及得知发生突变的频率范围。

(2)根据有损数据的处理分析结果，可以发现：连续小波变换，模极大值法和 à Trous 算法，三种方法处理损伤数据都会看到奇异性的存在，但是基于离散二进小波变换原理的à Trous算法，其每级分解系数和原时间序列的长度保持一致，不但具有平移不变性，而且可以保证奇异性检测的准确性。

(3)根据本文研究结果，所用的 à Trous 算法对于原始数据以及原始数据分解后的各频段数据处理结果，奇异点的时间位置大致一致，误差也相对较小。从数据对比中还能够发现，有损数据的高频段信号的处理结果展示了更好的奇异点的性质和特征，这与之前的理论相吻合。因此，à Trous方法可以应用于铁轨剥落磨损等损伤检测，并能给出损伤位置信息，可以较为方便地确定损伤位置。

致谢

感谢西南交大铁发公司对于本研究的技术和实验支持。

[1] LI Y, WILSON J, TIAN G Y. Experiment and simulation study of 3D magnetic field sensing for magnetic flux leakage defect characterisation[J]. NDT & E International, 2007, 40(2):179-184.

[3] SONG Z, YAMADA T, SHITARA H, et al. Detection of damage and crack in railhead by using eddy current testing[J]. Journal of Electromagnetic Analysis and Applications, 2011, 3(12):546-550.

[4] EDWARDS R S, DIXON S, JIAN X. Characterisation of defects in the railhead using ultrasonic surface waves[J]. NDT & E International, 2006,39(6): 468-475.

[5] COCCIA S, PHILLIPS R, NUCERA C, et al. UCSD/FRA non-contact ultrasonic guided-wave system for rail inspection an update [C]// Proceedings of SPIE—The International Society for Optical Engineering, 2011.

[6] KENDERIAN S, DJORDJEVIC B B, CERNIGLIA D, et al. Dynamic railroad inspection using the laser-air hybrid ultrasonic technique[J]. Non-Destructive Testing and Condition Monitoring,2006, 48(6): 336-341.

[7] BRUZELIUS K, MBA D. An initial investigation on the potential applicability of Acoustic Emission to rail track fault detection[J]. NDT & E International, 2004, 37(7): 507-516.

[8] BOLLAS K, PAPASALOUROS D, KOUROUSIS D, et al. Acoustic emission monitoring of wheel sets on moving trains[J]. Construction and Building Materials, 2013,48:1266-1272.

[9] HESSE D, CAWLEY P. Surface wave modes in rails[J]. Acoustical Society of America, 2006,5(15):733-740.

[10] CHONG M L, JOSEPH L R, YOUNHO C. A guided wave approach to defect detection under shelling in rail[J]. NDT & E International,2009,42:174-180.

[11] COCCIA S, BARTOLI I, MARZANI A, et al. Numerical and experimental study of guided waves for detection of defects in the rail head[J].NDT & E International,2011, 44:93-100.

[12] 何浩祥,孙立,闫维明,等.基于小波分析的结构损伤信号奇异性检测[J].工业建筑,2007(增刊1):204-207. HE Haoxiang, SUN Li, YAN Weiming, et al. Singularity detection for structural damaged signals based on wavelet analysis[J]. Industrial Construction,2007(Sup1):204-207.

[13] 张悦,杜守军,张丽梅. 小波奇异性在钢结构损伤检测中的应用[J]. 河北科技大学学报,2010,31(2):151-157. ZHANG Yue, DU Shoujun, ZHANG Limei. Application of wavelet singularity to steel structural damage detection[J]. Journal of Heibei University of Science and Technology,2010,31(2):151-157.

[14] 邱颖,任青文,朱建华. 基于小波奇异性的梁结构损伤诊断[J]. 工程力学,2005(增刊1):146-151. QIU Ying, REN Qingwen, ZHU Jianhua. A beam damage diagnosis based on wavelet singularity[J]. Engineering Mechanics,2005(Sup1):146-151.

[15] YAMAGISHI S, ICHIKI M, FUJIMOTO S,et al. Characterization of the piezoelectric power generation of PZT ceramics under mechanical force[C]//2013 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS. DTIP,2013.

[16] SAKAMOTO W K, MARIN-FRANCH P, TUNNICLIFFE D,et al. Lead zirconate titanate/polyurethane (PZT/PU) composite for acoustic emission sensors[C]//Conference on Electrical Insulation and Dielectric Phenomena (CEIDP). Annual Report:20-23.

[17] SONG G, GU H, MO Y L, et al. Concrete structural health monitoring using embedded piezoceramic transducers[J]. Smart Materials and Structures, 2007, 16(4): 959.

[18] QIU L, YUAN S F, SHI X L,et al. Design of piezoelectric transducer layer with electromagnetic shielding and high connection reliability[J]. Smart Materials and Structures,2012, 21(7): 075032.

Rail damage detection method based on acoustic emission and wavelet singularity

SONG Yang1, WU Fan1, LIU Dekou1, LIU Xiaozhou2, NI Yiqing2

(1. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Intelligent Structural Health Monitoring R&D Centre, The Hong Kong Polytechnic University Shenzhen Research Institute, Shenzhen 518057, China)

Many major derail accidents are closely related to the rail damage, so the study on the rail flaw detection technology is particularly important nowadays. The study is aiming at analyzing and comparing the characteristics of signals data before and after destruction, collected by a damage detection system. The damage and defect were judged by the differences between the processed data of destructive signals and nondestructive ones in time and frequency domain and according to the energy spectrum features. What’s more, the locations of defects and damages were obtained by virtue of the singularities of destructive signals using three wavelet singularity analysis methods, including continuous wavelet transform, Mallat algorithm and à Trous algorithm. It is found that à Trous algorithm can give quite accurate information about real damage locations, which shows that this method can be used in the real damage detection for rails and provide us more precise defect location information.

rail; nondestructive test (NDT); accoustic emission (AE); singularity detection

国家自然基金项目(51278300;61227011);深圳科技部基金项目(CXZZ20140508140740862)

2015-07-14 修改稿收到日期：2015-09-25

宋阳 男，硕士生，1990年10月生

吴凡 女，博士，副研究员，1963年6月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.02.032