恒星干涉仪延迟线系统地面随机振动响应分析

许明明， 季杭馨， 徐 腾， 章华涛， 吴 桢

(1.中国科学院 国家天文台南京天文光学技术研究所，南京 210042；2. 中国科学院 天文光学技术重点实验室，南京 210042)

恒星干涉仪延迟线系统地面随机振动响应分析

许明明1,2， 季杭馨1,2， 徐 腾1,2， 章华涛1,2， 吴 桢1,2

(1.中国科学院 国家天文台南京天文光学技术研究所，南京 210042；2. 中国科学院 天文光学技术重点实验室，南京 210042)

研究地面随机微振动对恒星干涉仪关键部件-光学延迟线系统性能的影响。利用美国蓝氏(Lansmont)集团生产的SAVER 3X型三轴振动仪实测地面随机振动信号，以输出的G加速度功率谱密度为激励，运用Workbench有限元分析软件计算该结构系统的随机振动响应；根据抛物镜面节点数据拟合出抛物镜面的Zernike多项式系数、抛物镜刚体平移量和抛物镜面PV和RMS值；将Zernike多项式系数导入光学系统中分析光学延迟线系统光学性能；最后利用ELCOWAT 3000电子自准直仪测量抛物镜刚体平移量，分析实际测量结果和计算理论结果偏差。分析计算结果与实验数据最大偏差7.6%，计算抛物镜面形RMS值为9.6 nm，PV值为46.1 nm，波前差为0.043λ。目前的光学延迟线的地面振动满足光学延迟线系统的稳定性要求。使用动态光学性能标准分析判断微振动对系统光学性能的影响程度，为恒星干涉仪其他子系统优化设计和隔振补偿措施提供参考。

光学延迟线；地面随机振动；有限元分析；Zernike拟合；光学性能

长基线恒星光干涉技术在国际上已经取得了长足的发展，但在我国尚没有可用于观测的仪器，国内对这一领域的研究相对落后[1]。目前国内从事恒星光干涉研究相关的单位有国家天文台、上海天文台、国家天文台南京天文光学技术研究所等。如国家天文台从事过天文光干涉相关研究的有郭红锋等；上海天文台朱能鸿院士、陈欣扬和周丹等从事天文综合孔径等方面研究；国家天文台南京天文光学技术研究所及前身南京天文仪器研制中心周必方、胡中文和吴桢等从事光干涉子系统主动镜、倾斜镜和光学延迟线等方面工作研究[1-3]。其他相关文献记载，从事天文光干涉相关研究的有中国科学院云南天文台刘忠，南京航天航空大学王海涛和中国计量学院范伟军等。

环境振动干扰影响高精度光学设备测量准确度和工作精度[4-5]，在干涉仪工作时，由于受到振动、大气扰动等各种因素的影响，使干涉仪两相干光束不在平行，结果导致获得的干涉条纹可见度大大降低[6-9]。恒星光干涉技术是高分辨率天文观测研究的主要技术方法之一。等光程和干涉光束波前平行时恒星干涉仪最终获得干涉条纹和测量结果的关键[10-12]。

光学延迟线系统作为恒星光干涉系统关键部件之一，对光程差进行实时补偿。同样受到振动等因素的影响，因此，对光学延迟线系统提出振动稳定性要求。本文采用有限元软件，建立光学延迟线模型，在分析其固有模态和固有频率基础上，以试验样机测量的实际地动功率谱密度为基础激励，运用Workbench 有限元分析软件的 Vibration 分析模块，计算该结构系统的随机振动响应，根据抛物镜面变形结果和延迟线光学系统性能为依据，对目前延迟线结构设计和地面环境进行综合评估。

1 延迟线系统的构成及振动测量

1.1 光学延迟线系统结构

光学延迟线在恒星干涉仪中的作用就是补偿干涉仪两臂之间的光程差，使光程差小于相干长度(条纹消失的临界光程差)。最常用的延迟线结构是基于Mark Ⅲ干涉仪的延迟线系统，但其机械和控制实现较为复杂[13]。本实验室借鉴欧南台的VLTI二级补偿系统，其设计光路和实际机械结构如图1所示。整个装置置于直线电机的精密运动平台上，延迟线整个系统放置于高精密光学减振平台上，星光以平行光束从抛物面光轴的一侧进入延迟线系统，然后从另一面射出。

图1 延迟线系统光路和结构Fig.1 The structure of optical delay line

1.2 地面随机振动基本原理与测量

在随机振动试验中， 任一瞬时各种频率成分的激励同时作用在反射镜组件上， 因此无法预测其瞬时的振动变化规律， 一般用整个加载周期内的均值均方根累计均方根和功率谱密度等统计量研究反射镜在随机振动试验中的响应[14]。

由于地面随机振动震谱频率一般低于50 Hz[15]。因此，按采样频率按大于2.5倍分析频率采样，但考虑到延迟线结构一阶固有频率为423.5 Hz，其输入激励信号的频谱不能过低，否则会导致无法有效激励结构振动。在实际随机振动测量中，使用美国蓝氏(Lansmont)集团生产的SAVER 3X型三轴振动仪采集其振动信号，采样频率为1 250 Hz。根据Workbench有限元软件的随机振动工具箱要求，激励功率谱密度有位移功率谱密度、速度功率谱密度、加速度功率谱密度等。本文以G加速度为激励功率谱密度，需要对采集的振动信号转换成G加速度功率谱密度，利用SAVER 3X型三轴振动仪自带软件SaverXware软件可直接输出G加速度功率谱密度，G加速度功率谱密度如图2所示。

图2 延迟线平台随机地面振动G加速度功率频谱密度Fig.2 Random vibration PSD of the mirror support plane

2 面随机运动响应分析

2.1 模态分析

为了保证仿真接近真实情况，以实验室样机为尺寸和材料选型依据，建立几何模型。在有限元模型中镜面材料为微晶玻璃，固定杆为低热膨胀系数的殷钢，其他材料均为铝合金。材料的参数见表1所示。

表1 材料参数[16]

模态即结构的固有频率和振型是进行振动频谱分析的一个重要过程，得到模态频率值和特征向量后，根据给定的基础振动功率谱密度计算每一个振动模型每一个自由度方向的模态响应幅值。将模态幅值作用于模态特征向量，可以得到每一个自由度方向的响应量。将各个模态下的响应叠加，就可以得到延迟线系统在激励下的响应，因此模态分析是随机振动的基础[17-18]。本文给出了前6阶模态，如表2所示。1～4阶振型如图3所示。

表2 延迟线结构固有频率

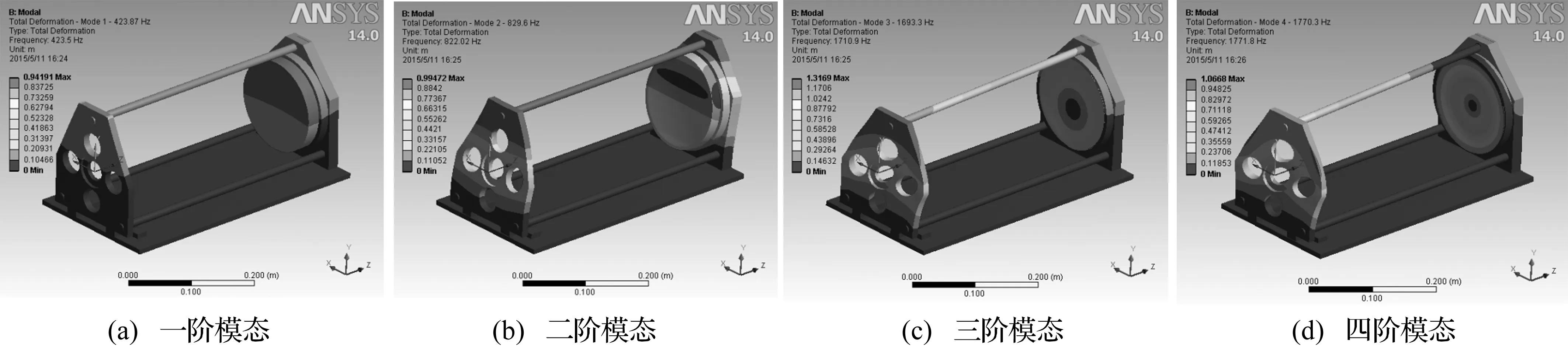
图3 1～4阶模态下的变形云图Fig.3 Model concurs from the first to the fourth

2.2 其次坐标变换法求解镜面平移及面形原理

在光机结构有限元分析数据中，设镜面一节点理想坐标(xi,yi,zi)沿x,y,z轴平移量分别为e,f,g，绕x,y,z轴旋转量分别为θx,θy,θz，由于旋转量非常小，忽略高阶项，总坐标变换矩阵T可如下表示：

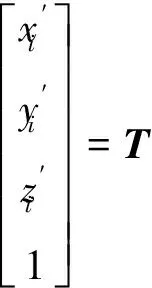
(1)

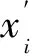
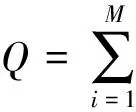
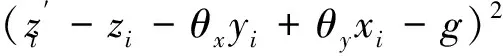
若想结果拟合误差最小，只要Q最小，由最小二乘法得到，要使Q最小，则需要：

根据上面六个方程组可以求出刚体平移量：

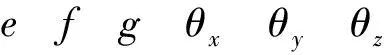
因此，可以求得总坐标变化矩阵T,就可以分离刚体位移，i节点变形前坐标整体移动到仅包含刚体位移的位置：

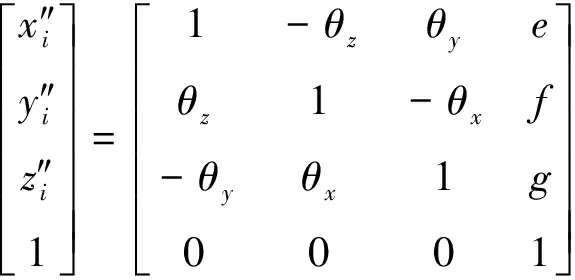
用有限元计算得到的节点面型数据，减去仅包含刚体位移的数据，就可以得到仅包含表面畸变的面型数据，即：

PV(绝对差值)值和RMS(平均值)值的定义可以得到[19]：

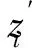
(2)

2.3 延迟线结构随机响应分析

随机振动频谱分析结构是该激励条件下的概率统计值，包括节点自由度的位置、速度及加速度的均方根值。计算随机载荷响应进行结构设计和优化及结构可靠性评估等是光学延迟线机械结构设计的重要任务。在实际工作中，仅抛物镜参与光线输入输出，因此分析抛物面镜镜面响应，可判断出光学延迟线系统性能。

因此，在响应分析过程中，选取抛物镜面作为研究对象，以实际X、Y、Z三个方向的随机地动功率谱密度作为输入见图2所示，研究抛物镜面形变，即光束经过抛物镜面后光波面形。在激励条件下，得到抛物面镜刚体平移结果见表3，抛物镜面在光轴方向的PV和RMS值见图4；在激励条件下，抛物镜面变形后拟合的Zernike多项式系数见表4，图5是将Zernike多项式系数和刚体平移量代入光学系统后的波前。

表3 抛物镜面刚体平移结果

图4 抛物镜面PV和RMS值Fig.4 The RMS value and RMS value

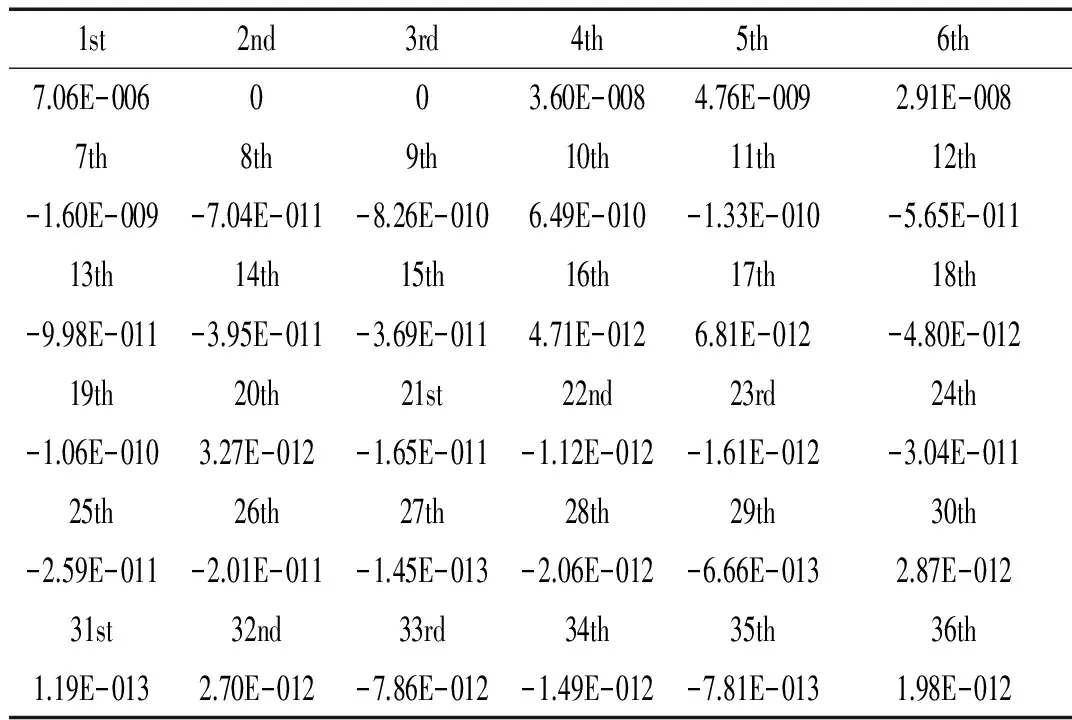
1st2nd3rd4th5th6th7．06E-006003．60E-0084．76E-0092．91E-0087th8th9th10th11th12th-1．60E-009-7．04E-011-8．26E-0106．49E-010-1．33E-010-5．65E-01113th14th15th16th17th18th-9．98E-011-3．95E-011-3．69E-0114．71E-0126．81E-012-4．80E-01219th20th21st22nd23rd24th-1．06E-0103．27E-012-1．65E-011-1．12E-012-1．61E-012-3．04E-01125th26th27th28th29th30th-2．59E-011-2．01E-011-1．45E-013-2．06E-012-6．66E-0132．87E-01231st32nd33rd34th35th36th1．19E-0132．70E-012-7．86E-012-1．49E-012-7．81E-0131．98E-012

由图4可知，抛物镜面PV值为46.1 nm，RMS值为9.6 nm。RMS值小于可见光波长(λ=632 nm)的λ/30，因此，根据经验分析可知，抛物镜面的变形对延迟线系统的光学性能影响较小。

图5 Wavefront图Fig.5 Wavefront

如图5(a)所示，理论设计要求出射光为平行光，因此像面波前差为0，由地面随机振动激励后，光学延迟线系统像面波像差为0.043λ。此时，光学系统像面wavefront差值为0.043λ。根据光学设计经验可知，光学系统波前差小于λ/16，光学系统性能影响可以忽略。因此，分析可知地面随机振动对光学系统影响较小。根据设计光路容差分析，抛物镜容差较大，如在Y方向，抛物镜中心容差在±0.01 mm内,对光学系统性能影响较小。根据理论分析Y方向抛物镜刚体平移为5.32E-008 m。因此，光学系统的波前差变化很小。当然在实际工作中，由于安装误差和加工误差等原因，抛物镜实际刚体平移会大于理论设计值，只要抛物镜中心偏差在容差范围内，均可以保证抛物镜实际工作性能。

表5是利用德国MÖLLER-WEDEL OPTICAL GmbH公司生产的ELCOWAT 3000电子自准直仪对抛物镜背面测量的准直镜整体偏移进行多次测量的结果，在X轴方向抛物镜实际刚体平移量平均值为：0.075 μm，在Y轴方向抛物镜实际刚体平移量平均值为：0.05 μm。

理论计算抛物镜刚体平移X和Y方向分别为8.07E-008 m和5.32E-008 m，比较计算结果和实测结果，最大误差为：

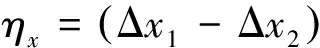
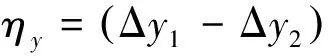
对比可知理论分析和实际测量结果最大大误差为7.6%，理论和实验误差在合理范围之内，说明本文理论分析数据较为可靠。

表5 抛物镜刚体平移测量结果

3 结 论

恒星干涉仪光学延迟线系统的地面微动响应分析是稳定性分析计算的重要环节，采用有限元软件，以实际测试的地面随机振动功率谱密度为激励，研究延迟线安装环境随地面随机振动响应分析。计算的抛物镜面刚体平移量和实际测量结果偏差小于7.6%，表明理论计算结果有效。根据理论分析的抛物镜面形结果和光路波前差的变化结果可知地面随机振动对光学延迟线系统影响较小，目前光学延迟线安装环境地面振动满足延迟线稳定性要求。

[1] 陈欣扬. Fizeau型天文光学综合孔径望远镜的若干关键技术[D].上海：中国科学院上海天文台, 2006.

[2] 郭红锋. 光干涉与综合孔径技术发展[J]. 紫金山天文台台刊, 2003, 22(1):99-105. GUO Hongfeng. Development on techniques of the optical interferometer and aperture synthesis[J]. Publications of Purple Mountain Observatory, 2003, 22(1):99-105.

[3] 吴桢, 李超, 林燮佳, 等. 长基线恒星光干涉技术中延迟线系统的设计与实验[J]. 中国科学:物理学力学天文学, 2012，42(2)：210-216. WU Zhen, LI Cao, LIN Xiejia, et al. Design and experiment of the delay line system for long baseline stellar interferometry[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2012, 42(2): 210-216.

[4] 邵珺，叶景峰，胡志云，等. 一种振动失调反射光线系统模拟计算的实验分析方法[J].振动与冲击, 2013, 32(12):72-75. SHAO Jun, YE Jingfeng, HU Zhiyun, et al. A test method for simulation calculation of a misaligned reflection optical system under vibration interference[J]. Journal of Vibration and Shock, 2013, 32(12):72-75.

[5] 佟志忠，段广仁，何景峰，等. 基于加速度各项同性的空间光学仪器主动隔振Stewart平台设计[J]. 振动与冲击,2012,31(2):109-114. TONG Zhizhong, DUAN Guangren, HE Jingfeng, et al. Optimal design of an acceleration isotropy-based active vibration isolation stewart platform for spaceborne optical instrument[J]. Journal of Vibration and Shock, 2012, 31(2):109-114.

[6] 余向志，李政勇，王志豪，等. 温度和振动对光纤马赫-曾德干涉仪的影响与动态补偿研究[J].光子学报, 2012, 41(9):1041-1046. YU Xiangzhi, LI Zhengyong, WANG Zhihao,et al. Effect of temperature and vibration on optical fiber interferometer and dynamic compensation[J]. Acta Photonica Sinica, 2012, 41(9): 1041-1046.

[7] 陆艺，范伟军，孔明. 恒星干涉仪主动镜转角的检测[J].光子学报, 2010, 39(6):1111-1115. LU Yi, FAN Weijun, KONG Ming. Measuring the tip/tilt angles of the active mirror in the stellar interferometer[J]. Acta Photonica Sinica, 2010, 39(6): 1111-1115.

[8] 孙后环, 周必方, 蒋筱如. 恒星光干涉仪倾斜镜系统的研制[J]. 分析测试技术与仪器, 2000, 6(3): 148-153. SUN Houhuan, ZHOU Bifang, JIANG Xiaoru. Research on tip-tilt mirror system used in stellar interferometer [J]. Analysis and Testing Technology and Instruments, 2000, 6(3): 148-153.

[9] 吴栋，朱日宏，陈磊，等. 干涉仪环境振动的外差检测与自适应控制[J].光子学报, 2004, 33(12):1493-1496. WU Dong, ZHU Rihong, CHEN Lei, et al. Heterodyne measurement and adaptive control for environmental micro-vibration in phase-shifting interferometer[J]. Acta Photonica Sinica, 2012, 41(9): 1041-1046.

[10] 王海涛, 周必方. 天文光干涉技术[J]. 光学精密工程, 2003, 11(4): 320-325. WANG Haitao, ZHOU Bifang. Astronomical optical interference technology[J]. Optics and Precision Engineering, 2003, 11(4): 320-325.

[11] 金岩，郝志勇. 针对通过噪声的空滤器声学特性研究与改进[J]. 浙江大学学报(工学版)，2006, 40(8): 1143-1145. JIN Yan, HAO Zhiyong. Investigation and improvement of air-in filter acoustic performance towards pass-by noise [J]. Journal of Zhejiang University(Engineering Science), 2006, 40(8): 1143-1145.

[12] 王海涛, 范伟军, 蒋筱如, 等. 恒星光干涉仪中主动镜的研究[J]. 光学技术, 2002, 28(4): 334-336. WANG Haitao, FAN Weijun, JIANG Xiaoru, et al. Research on the active mirror system of the stellar interferometer[J]. Optical Technique, 2002, 28(4): 334-336.

[13] 左韩露, 陈忆. 恒星光干涉仪中光学延迟线的结构设计[J]. 机械设计与制造, 2009, 2 (2): 22-24. ZUO Hanlu,CHEN Yi. The improvements of the optical delay lines in stellar interferometers[J]. Analysis and Testing Technology and Instruments, 2009, 2(2): 22-24.

[14] 董德义，辛宏伟，杨利伟，等. 大孔径反射镜组件随机振动响应分析与试验[J].振动与冲击，2011，30(11):74-78. DONG Deyi, XIN Hongwei, YANG Liwei, et al.Random vibration analysis and its verification for large aperture mirror component[J]. Journal of Vibration and Shock,2011,30(11):74-78.

[15] 冯斌, 周忆, 张军伟, 等. 大型精密镜架地面随机微振动响应分析[J]. 光学精密工程, 2007, 15(3): 356-361. FENG Bin, ZHOU Yi, ZHANG Junwei, et al. Analysis on ground random vibration response of large-scale precision mirror mount [J]. Optics and Precision Engineering,2007, 15(3): 356-361.

[16] BELY P. The design and construction of large optical telescopes[M]. New York: Springer Verlag, 2003.

[17] 于旭东, 龙兴武, 汤建勋. 机械抖动激光陀螺的随机振动响应分析[J]. 光学精密工程, 2007,15(11): 1760-1766. YU Xudong, LONG Xingwu, TANG Jianxun. Random vibration analysis of mechanically dithered ring laser gyroscope [J]. Optics and Precision Engineering, 2007, 15(11): 1760-1766.

[18] 王洪伟, 阮萍, 徐广州, 等. 某空间望远镜相关跟踪系统摆镜随机振动分析[J].光子学报, 2009, 38(12):3226-3229. WANG Hongwei, RUAN Ping, XU Guangzhou,et al. Random vibration analysis of tip/tilt mirror in a space telescope correlation tracking system[J]. Acta Photonica Sinica, 2009, 38(12): 3226-3229.

[19] 李贤辉. 光机集成有限元分析光学面形后处理研究与实现[D].长春：中科院长春光学精密机械与物理研究，2004.

Random ground vibration response of the optical delay line system of a stellar interferometer

XU Mingming1,2, JI Hangxin1,2, XU Teng1,2, ZHANG Huatao1,2, WU Zhen1,2

(1.National Astronomical Observatories Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences, Nanjing 210042, China;2.Key Laboratory of Astronomical Optics & Technology, Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences, Nanjing 210042, China)

The stability problem of an optical delay line system caused by random ground vibration was concerned. The random ground vibration signal andGacceleration power spectral density(PSD) were measured and the random vibration response of the mount was analyzed with the PSD module of Workbench finite element software. The Zernike polynomial coefficient, the translation of rigid body, the root mean square(RMS) value and peak-valley (PV) value of the parabolic reflector were calculated by fitting the nodes data. Introducing the Zernike polynomial coefficient into the optical system, the optical performance of the optical delay line system was analyzed. The rigid body translation of the parabolic reflector was measured by ELCOWAT 3000 Electronic Autocollimators. The analysis results show that the largest analytical errors with respect to the simulation and experiment are 7.6%. The RMS value is 9.6 nm, and PV value is 46.1 nm. The error of wavefront is 0.043λ. The actual vibration level of the installation base meets the stability requirement of the optical delay line system. The research on the relationship between the optical performance and the random vibration provides important reference to the optimal design and vibration isolation of other optical systems of stellar interferometers.

optical delay line system; random vibration; finite element analysis; Zernike fitting; optical performance

国家自然科学基金(11190011;11473047;11273038;11473048;11473049;11603054);中国科学院天文光学技术重点实验室开放课题基金( CAS-KLAOT-KF201307)

2015-09-21 修改稿收到日期：2016-01-13

许明明 男，博士，工程师,1981年生 E-mail:mingxu@niaot.ac.cn

P111.47

A

10.13465/j.cnki.jvs.2017.02.026