基于谐波平衡法的摆线钢球行星传动等速输出机构非线性动态特性研究

杨荣刚, 安子军

(燕山大学 机械工程学院，秦皇岛 066004)

基于谐波平衡法的摆线钢球行星传动等速输出机构非线性动态特性研究

杨荣刚, 安子军

(燕山大学 机械工程学院，秦皇岛 066004)

为揭示摆线钢球行星传动等速输出机构的非线性动力学行为，建立考虑机构钢球数目、输入激励、啮合副啮合状态及啮合刚度的纯扭转强非线性动力学模型。将啮合副预紧函数表现为多项式的形式，将啮合副间隙函数表达为描述函数的形式，通过谐波平衡法将微分方程组转化为非线性代数方程组，利用MATLAB进行求解，得到系统的基频稳态响应。通过改变钢球数、轴向压缩量与啮合刚度，分析参数变化对系统非线性特性的影响。结果表明，预紧系统只有两阶频率激发共振，系统非线性程度随钢球数、啮合刚度和预紧量的增加而减弱，预紧量是影响系统非线性程度的主要因素；间隙系统激发共振频率的阶数与钢球数目有关，幅频响应曲线出现典型非线性特征，出现单边冲击与双边冲击现象。基于多项式函数的谐波平衡法为深入研究摆线钢球行星传动系统的动态特性提供了一种有效方法。

摆线钢球行星传动；等速输出机构；谐波平衡法；幅频特性；轴向预紧；非线性振动

摆线钢球行星传动与摆线针轮等活齿传动相比，能够实现啮合副的实时无隙啮合，从而实现精密传动；与齿轮系统相比，除精密传动外，还具有啮合效率高、噪声低、结构紧凑易于微型化等突出特性。因此，在高精密传动应用领域有着重要价值和发展前景[1-2]。

文献[3-4]建立了摆线钢球行星传动啮合副两点接触状态下的平移-扭转耦合动力学模型。文献[3]揭示了系统的固有特性，并分析摆线钢球行星传动的主要结构参数对固有频率的影响；文献[4]运用多尺度法对系统进行动力稳定性分析，并利用摄动法计算出系统的稳态响应。以上文献尚未对钢球数目变化、轴向预紧与啮合状态对机构非线性振动的影响进行研究，以及多尺度法与摄动法适用于弱非线性系统。因此，在不同钢球数、轴向压缩量、刚度系数及啮合状态下建立摆线钢球行星传动等速输出机构非线性动力学模型，并采用合适的非线性分析方法进行研究，有一定的研究价值。

谐波平衡法是求解非线性振动常用的一种近似解析法，不仅限于弱非线性系统，且该种方法的求解过程归结为代数方程组的求解，不需要求解微分方程组或积分-微分方程组，采用谐波平衡法对等速输出机构的非线性动态特性进行分析，结果更为准确。文献[5]根据齿轮间隙函数,将相平面划分为三个区域并建立相对应的Poincaré映射,结合谐波平衡法及序列二次规划方法求得区域内的解,并分析不同因素对齿轮冲击响应的影响。文献[6]应用HBM与离散傅里叶变换分析了含有齿侧间隙的两级定轴齿轮传动系统，以及行星齿轮传动系统的非线性动态特性。文献[7]在刚度波动的情况下，推导了行星齿轮系统微分方程组的解析谐波平衡法的计算公式，利用基于描述函数的HBM法研究动态特性,并分析时变啮合刚度、误差和齿侧间隙对系统非线性动力学特性的影响。文献[8]将齿侧间隙非线性函数表达为描述函数的形式，运用谐波平衡法得到系统的基频稳态响应，通过改变时变啮合刚度、齿侧间隙与综合啮合误差，分析参数变化对系统非线性动态特性的影响。

本文以啮合副处于不同啮合状态的系统为研究对象，建立考虑钢球数、啮合刚度、输入转矩与轴向预紧量的纯扭转非线性动力学模型。通过谐波平衡法将微分方程组转化为非线性方程组，运用MATLAB进行求解，得到系统的基频稳态响应，分析钢球数目、啮合刚度与轴向预紧量对系统非线性动态特性的影响。

1 动力学模型建立

等速输出机构由行星盘、等速钢球、输出轴等组成，如图1所示。O1、O3分别为行星盘、输出轴回转中心。运转时行星盘做行星运动，行星盘环形槽推动钢球滚动，钢球推动输出轴定轴转动，实现转速输出。

行星盘与输出轴做定轴转动时，传动简图如图1(b)所示。为实现机构的实时无隙精密传动，环形槽均采用双圆弧结构(使用两把不同铣刀分别加工环形槽内外侧，使环形槽纵切面内、外侧曲率半径不同)，如图1(c)所示。在偏心距一定情况下，通过改变内(外)侧环形槽曲率半径，获得不同的啮合刚度，可实现内、外侧啮合刚度变化。

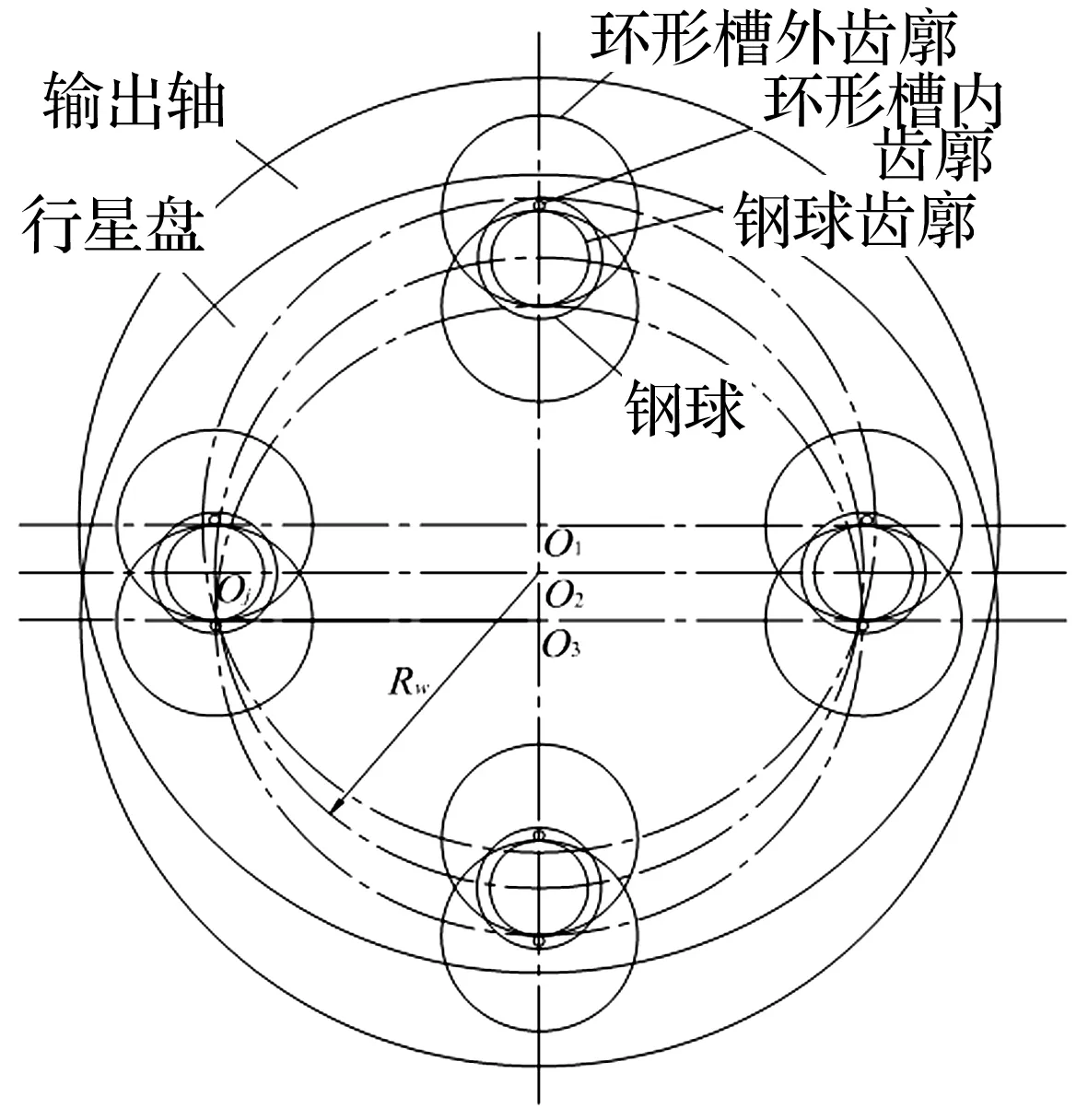
(a) 等速啮合副结构图

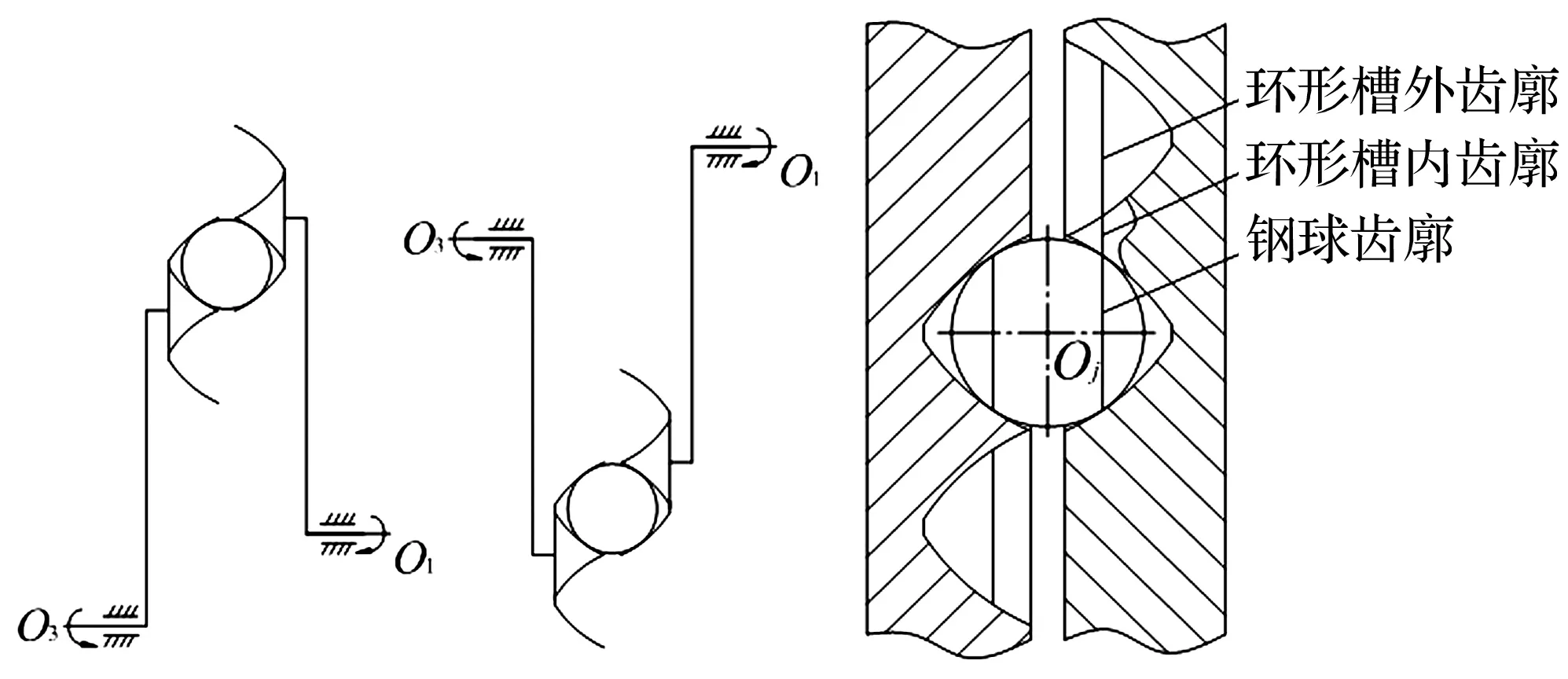
(b) 等速啮合副传动原理图 (c) 环形槽结构图图1 等速啮合副图Fig.1 Constant velocity engagement pair

1.1 动力学模型

等速输出机构各构件减掉输入轴转速ωr，使得各构件转化为定轴转动，行星盘绕O3旋转，各钢球均绕O2旋转，输出轴绕O1旋转。此时，考虑行星盘、输出轴、钢球的旋转自由度，建立如图2所示的等速输出机构非线性纯扭转动力学模型。脚标3、4j、5分别指行星盘、第j个钢球、输出轴。u3、u5、u4j为行星盘、输出轴、第j个钢球的角位移，φj=ωt+2π/Z4第j个钢球转过角度，Z4钢球数，ω角速度，Rw钢球回转半径。

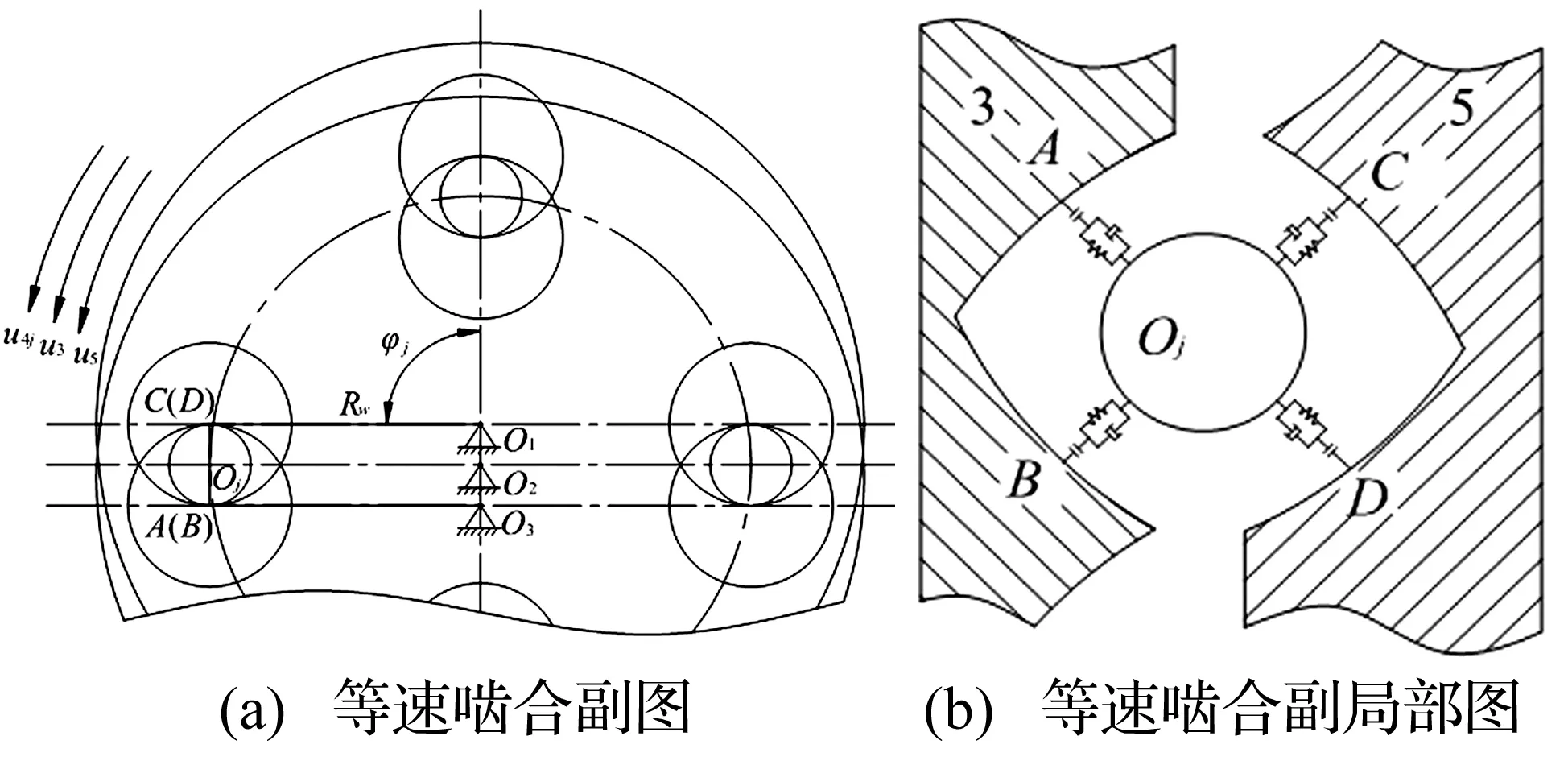
图2 等速啮合副动力学模型Fig.2 Constant velocity engagement pair dynamic model

1.2 啮合点相对位移

在间隙调节机构作用下，输出轴轴向移动实现啮合副预紧。输出轴相对行星盘轴向移动量为δz，啮合点法向压缩量为δ=δzsinβ/2(β对应取值β1或β2，β1、β2分别指外、内侧啮合点法线与盘平面夹角)，将其折合成角位移为u=δ/(Rwcosβ)。将δz=0定义为A、B、C、D四点均啮合且法向力为零，δz<0啮合副存在间隙，δz>0啮合副存在预紧(压缩)量。摆线钢球行星传动存在间隙调节机构，该机构输出轴向位移且足以抵消啮合副产生的磨损量时，啮合副处于预紧状态，δ>0；输出轴向位移为负，或者轴向位移量不足以抵消啮合副产生的磨损量时，啮合副处于间隙状态，δ<0。

定义构件间相对位移在运动方向上的投影为

1.3 量纲一化微分方程组

系统的非线性动力学微分方程组为

(1)

式中f(um,u)为预紧或间隙非线性函数(m=1j,2j);Ji为构件绕回转中心的转动惯量(i=3,4j,5);Ti为构建中传递的转矩(i=m,s,c)。

扭转刚度非线性函数为

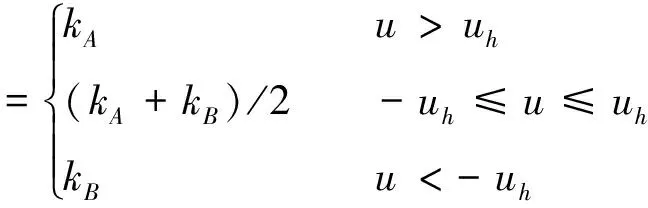
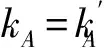
预紧非线性函数统一形式为

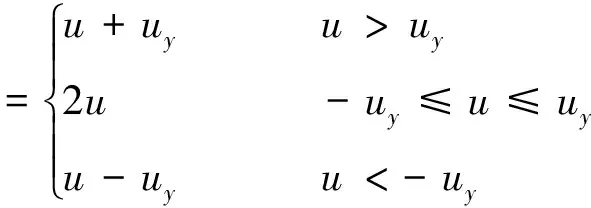
式中uy为啮合副预紧量转化角位移一半;u为相对角位移u1j与u2j。

间隙非线性函数统一形式为

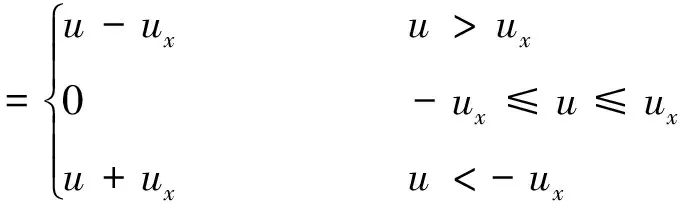
式中ux为啮合副齿侧间隙转化角位移一半。

对式(1)进行坐标变换可得

(2)

引入特征频率ωn

进一步定义

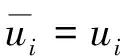
量纲一化式(2)，得到如下微分方程组

(3)

量纲一化预紧非线性函数统一形式为

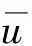
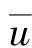
根据文献[9]中用多项式替代啮合刚度分段函数，及文献[10]与文献[11]将间隙非线性函数用多项式函数替换，将预紧非线性函数用多项式函数替换得

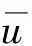
量纲一化间隙非线性函数统一形式为[12]

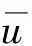
(5)

2 谐波平衡法求解

在多数情况下，系统的基频稳态响应往往占据主导地位，最关注系统的基频稳态响应。对于系统的一次谐波稳态响应，其近似表达式为

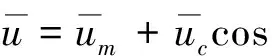
(6)

速度与加速度分别为

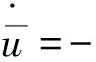
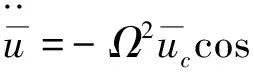
将式(5)用Fourier级数展开为

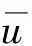
(7)

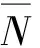
将式(4)与式(6)代入式(3)，或者将式(7)代入式(3)，令两边常数项、cosΩτ项、sinΩτ项分别相等，均可得到如下形式的方程组

(8)

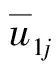
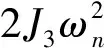
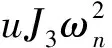
通过谐波平衡法将微分方程组转化为非线性方程组，式(8)所示，然后运用MATLAB中fsolve命令，通过对Ω设定步长逐个描点求解该非线性方程组。

3 频域动态特性

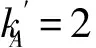
将啮合副处于预紧状态的等速输出机构简称为预紧系统，将啮合副处于间隙状态的等速输出机构简称为间隙系统。U341是指行星盘与第一个钢球的量纲一位移响应幅值，U451是指第一个钢球与输出轴的量纲一位移响应幅值。线性系统、预紧系统与间隙系统幅频响应曲线如图3所示。由图可知在低频范围内，线性系统与预紧系统两阶频率激发共振，间隙系统六阶频率激发共振。轴向预紧量δz=100 μm时，预紧系统激发共振频率与线性系统固有频率存在偏差，两阶频率均向高频方向移动，幅频响应曲线会出现多值的非线性特征，存在无冲击与单边冲击现象。间隙系统较多低阶频率激发共振，幅频响应曲线出现幅值跳跃、多值解及亚谐共振的典型非线性特征，存在无冲击、单边冲击与双边冲击现象。对比可知，间隙系统非线性程度明显强于预紧系统。由于通过设定步长对Ω逐个描点求解式(7)，图中会出现不连续点或散点，表明在该处存在幅值跳跃或多值解，反映出系统的非线性动态特性。非线性因素的引入，使得非线性系统非线性特性明显区别于线性系统。

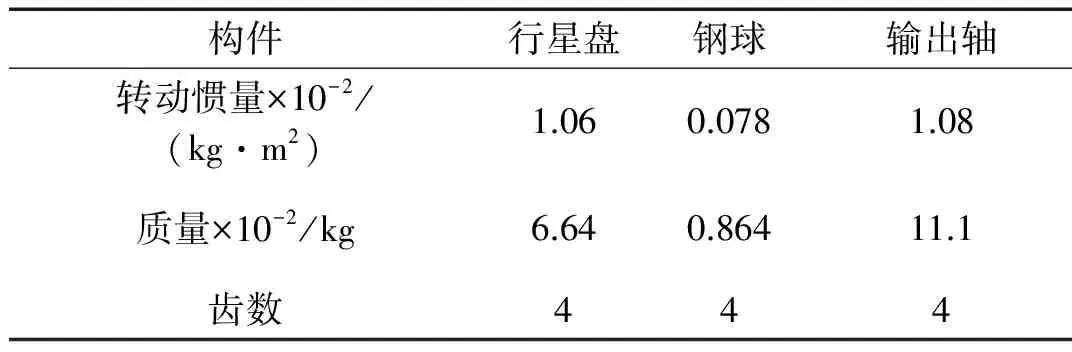
表1 系统参数值

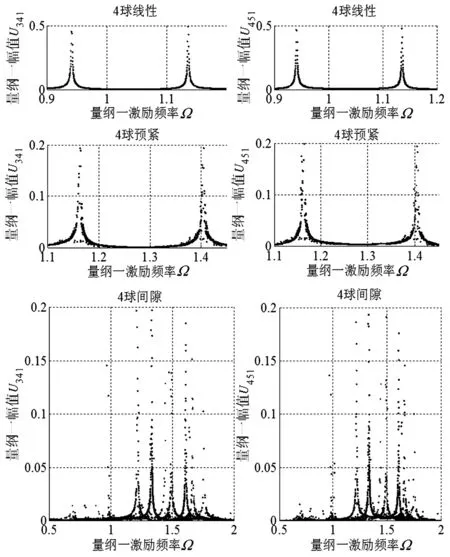
图3 幅频响应曲线Fig.3 Amplitude frequency response curve

4 系统参数对动态特性的影响

4.1 钢球数目的影响

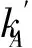
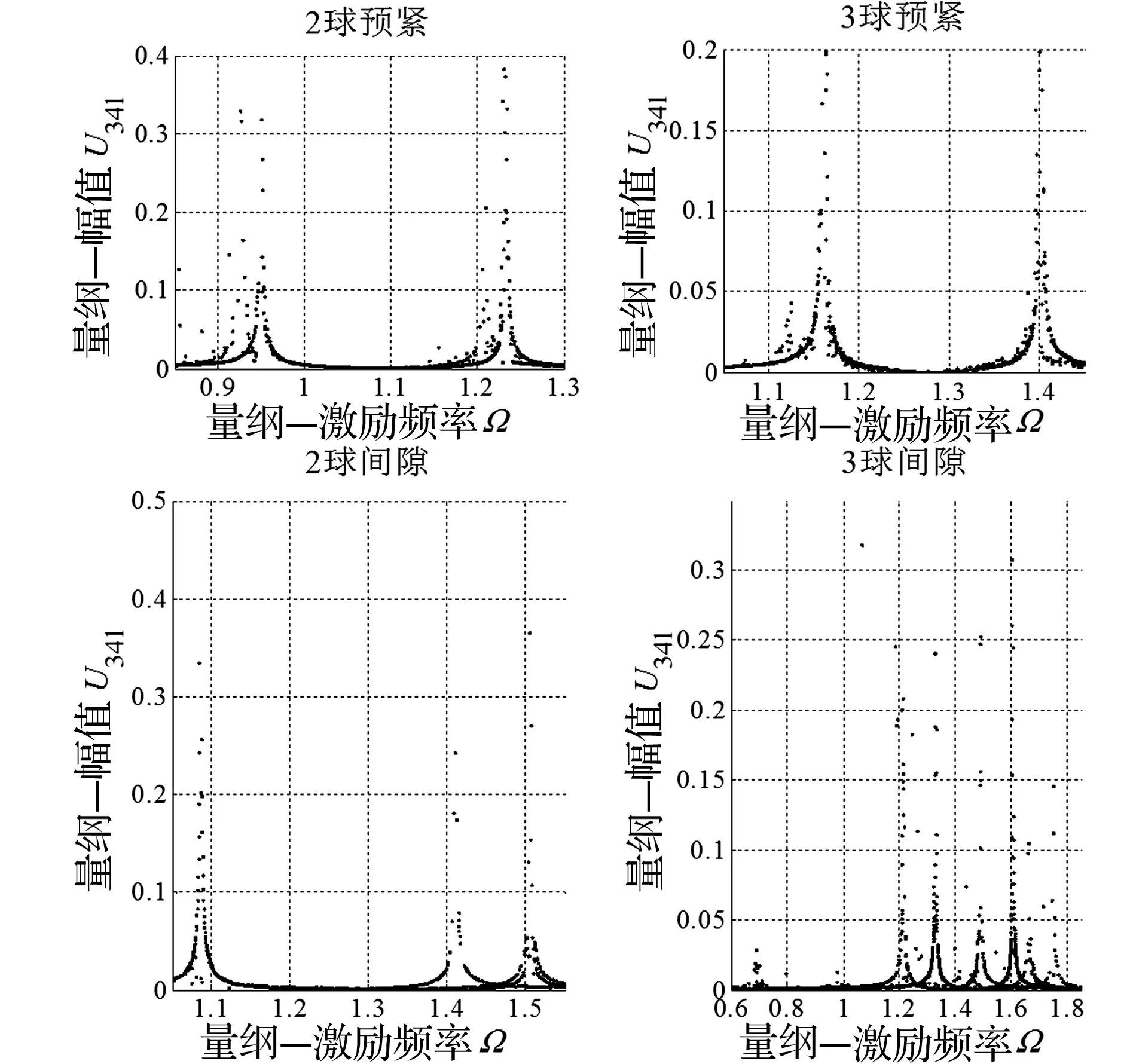
图4 钢球数对幅频响应影响Fig.4 The influence of ball number on the amplitude frequency response

两钢球预紧系统(预紧系统只有两个钢球)两阶频率激发共振，幅频响应曲线存在较多散点，主要在区间(0.884,0.916)、(1.166,1.198)与(1.241,1.272)内发生单边冲击，约在1.225处发生幅值跳跃；三钢球预紧系统两阶频率激发共振，单边冲击主要发生在区间(1.375,1.393)中，其余区间存在较多不连续点及少量散点；四钢球预紧系统幅频响应曲线出现较多不连续点，存在单边冲击现象。两钢球间隙系统三阶频率激发共振，存在较少不连续点，在区间(1.317,1.485)内发生单边冲击，在区间(1.485,1.497)与(1.511,1.596)内发生双边冲击；三钢球间隙系统六阶频率激发共振，在Ω=0.673处发生较为明显的亚谐共振，在区间(1.02,1.73)内幅频响应曲线变化较为复杂，存在单边冲击与双边冲击；四钢球间隙系统激发出较多亚谐共振，冲击特性较三钢球系统复杂。不同数目钢球预紧(间隙)系统，频响曲线中均会出现多值解，表明钢球数目变化不会影响等速输出机构的冲击特性。预紧系统中，随着钢球数目的增加，系统振动的最大幅值减小，激发共振的各阶频率向高频方向移动，三球与四球系统激发共振的各阶频率相差较小，两钢球系统幅频响应曲线相对较复杂，表现出相对较强的非线性特征；三球与四球间隙系统激发共振的各阶频率相差较小，出现幅值跳跃与多值解的典型非线性特征，且存在亚谐共振，冲击特性较复杂，非线性程度均强于两球间隙系统。由以上分析可知，输出机构为获得较小振动与噪声，需保证间隙调节机构实时消除齿侧间隙。

4.2 预紧量的影响

轴向预紧量为δz=10 μm时，幅频响应曲线存在较多散点，非线性程度较强；δz=40 μm时，频响曲线存在少量散点与较多不连续点，冲击特性表现出一定的规律性；δz=70 μm时，幅频响应曲线有较强的变化规律，单边冲击主要发生在区间(1.102,1.134)、(1.172,1.211)、(1.332,1.374)与(1.421,1.466)内，在共振频率附近出现少量不连续点；δz=100 μm时，单边冲击对应激励频率区间减小，主要分布在区间(1.105,1.133)与(1.401,1.423)内，非线性程度变弱。随着轴向预紧量逐渐增加，振动幅值逐渐减小，散点减少，出现冲击现象的激励频率范围减小，非线性程度逐渐减弱。

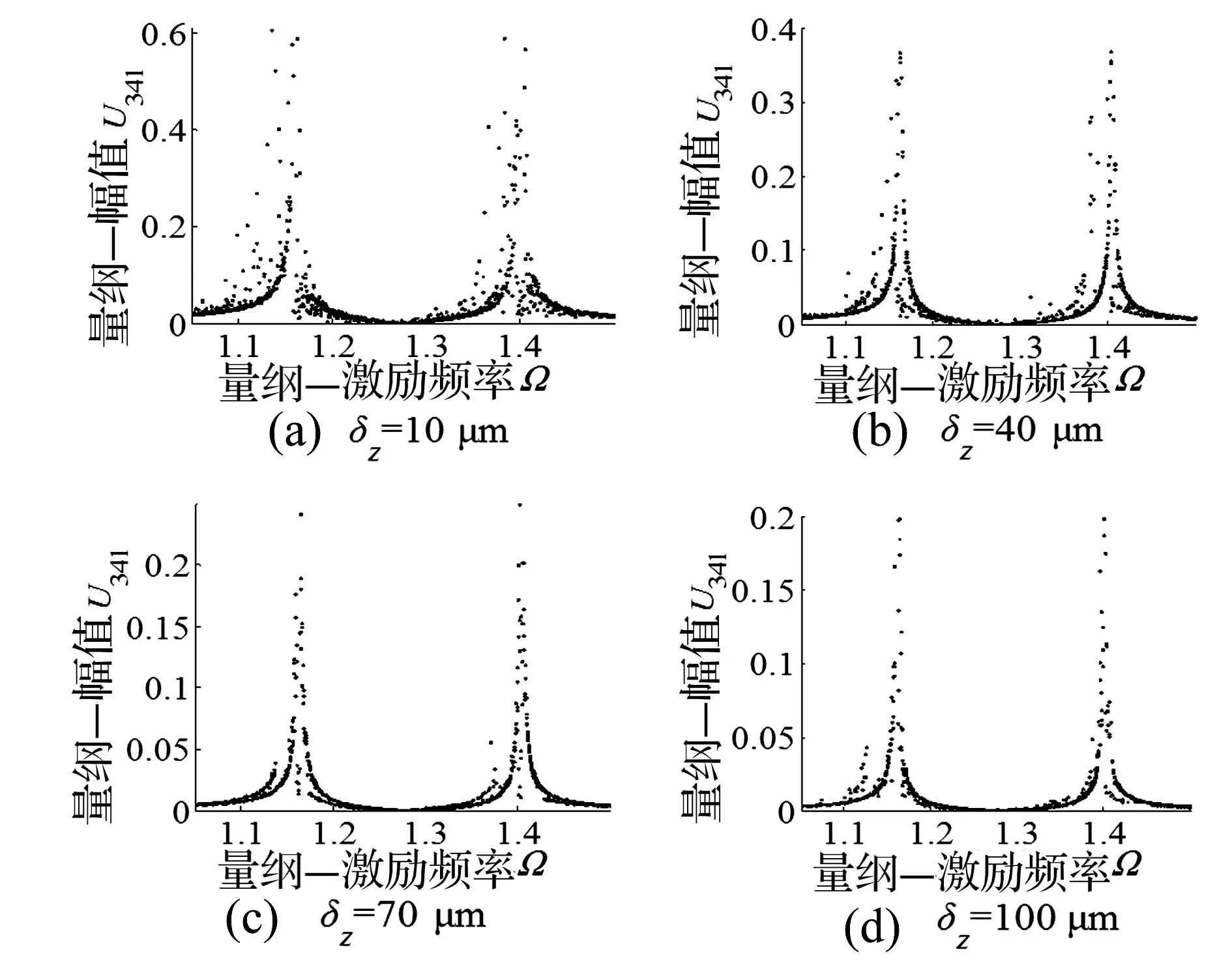
图5 轴向预紧对幅频响应影响Fig.5 The influence of axial preload on the amplitude-frequency response

4.3 啮合刚度的影响

三钢球预紧系统中，轴向预紧为50 μm，步长设为ΔΩ=0.000 4，啮合刚度变化时，频响曲线如图6所示。

图6 啮合刚度对幅频响应影响Fig.6 The influence of mesh stiffness on amplitude frequency response

5 结 论

根据对本文建立的等速输出机构非线性纯扭转动力学模型进行的研究，得到如下结论：

(1)等速输出机构啮合副啮合状态不同(间隙或预紧)，系统均出现复杂的冲击现象。预紧系统幅频特性曲线出现多值解与单边冲击非线性特征，间隙系统幅频特性曲线出现多值解、单边冲击、双边冲击的典型非线性特征，两系统非线性特征存在明显区别。

(2)预紧系统在低频范围内只有两阶频率激发共振，该两阶频率除随钢球数目增加向高频方向移动之外不随其它参数的改变而发生变化；间隙系统激发共振的频率阶数随钢球数目变化而发生变化，三钢球与四钢球间隙系统均会产生亚谐共振。

(3)预紧系统中，轴向压缩量、啮合刚度与钢球数增加，会使系统振动幅值减小、非线性现象表现程度减弱，轴向预紧量变化对系统的动态特性影响最大。钢球数目增加，间隙系统振动幅值减小，非线性现象表现程度增强。

[1] 王国彪，赖一楠，范大鹏，等. 新型精密传动机构设计与制造综述. 中国机械工程，2010, 21(16):1891-1897. WANG Guobiao, LAI Yinan, FAN Dapeng, et al. Summary of new type precision transmission design and manufacture[J]. China Mechanical Engineering, 2010, 21(16):1891-1897.

[2] 徐盛林，陈耿. 精密超精密定位技术及其应用[J]. 中国机械工程，1997, 8(4):73-75. XU Shenglin, CHEN Geng. Precision ultra-precision positioning technology and its applications[J]. China Mechanical Engineering, 1997, 8(4):73-75.

[3] 安子军，张鹏，杨作梅. 摆线钢球行星传动系统参数振动特性研究[J]. 工程力学，2012，29(3):244-251. AN Zijun, ZHANG Peng, YANG Zuomei. Research on properties for parametric vibration of cycloid ball planetary transmission system[J]. Engineering Mechanics, 2012, 29(3):244-251.

[4] 张鹏，安子军. 摆线钢球行星传动动力学建模与固有特性分析[J]. 中国机械工程，2014，25(2):157-162. ZHANG Peng, AN Zijun. Dynamics model and natural characteristics of cycloid ball planetary transmission[J]. China Mechanical Engineering, 2014, 25(2):157-162.

[5] 陈思雨，唐进元，谢耀东. 齿轮传动系统的非线性冲击动力学行为分析[J]. 振动与冲击，2009，28(4)：70-75. CHEN Siyu, TANG Jinyuan, XIE Yaodong. Analysis of nonlinear impact dynam ic behavior for agear pair system with tim evarying stiffness and friction[J]. Journal of Vibration and Shock，2009，28(4)：70-75.

[6] AL-SHYYAB A，KAHRAMAN A. A non-linear dynamic model for planetary gear sets[J]. Proceedings of the Institution of Mechanical Engineers，Part K:Journal of Multi-body Dynamics，2007，221(4)：567-576.

[7] 孙涛，沈允文，孙智民，等. 行星齿轮传动非线性动力学方程求解与动态特性分析[J]. 机械工程学报，2002，38(3)：11-15. SUN Tao，SHEN Yunwen，SUN Zhimin，et al. Study on nonlinear dynamic behavior of planetary gear train solution and dynamic behavior analysis[J]. Journal of Mechanical Engineering，2002，38(3)：11-15.

[8] 巫世晶，刘振皓，王晓笋，等. 基于谐波平衡法的复合行星齿轮传动系统非线性动态特性[J]. 机械工程学报，2011，47(1)：55-61. WU Shijing，LIU Zhenhao，WANG Xiaosun，et al. Nonlinear dynamic characteristics of compound planetary gear train sets based on harmonic balance method[J]. Journal of Mechanical Engineering，2011，47(1)：55-61.

[9] 刘志峰，张志民，张敬莹，等. 基于多项式的等高齿锥齿轮时变啮合刚度建模[J]. 吉林大学学报(工学版)，2013，43(4): 139-144. LIU Zhifeng，ZHANG Zhimin，ZHANG Jingying，et al. Modelling of high-spiral bevel gear mesh stiffness based on polynomial[J]. Journal of Jilin University(Engineering and Technology Edition),2013，43(4):139-144.

[10] THEODOSSIADES S, NATSIAVAS S. Non-linear dynamics of dear-pair systems with periodic stiffness and backlash[J]. Journal of Sound and Vibration, 2000,229(2): 287-310.

[11] 马锐，陈予恕. 含裂纹故障齿轮系统的非线性动力学研究[J]. 机械工程学报, 2011,47(21):84-90. MA Rui, CHEN Yushu. Nonlinear dynamic research on gear system with cracked failure[J]. Journal of Mechanical Engineering, 2011,47(21):84-90.

[12] 刘志峰，郭春华，杨文通，等. 基于分段间隙函数的螺旋锥齿轮时变啮合参数分析[J]. 振动与冲击，2013，32(4):153-157. LIU Zhifeng，GUO Chunhua，YANG Wentong，et al. Time-varying meshing parameters analysis for spiral bevel gear based on sub-clearance function[J]. Journal of Vibration and Shock，2013，32(4)：153-157.

Nonlinear dynamic characteristics of the equal speed output mechanism of cycloid ball planetary transmission based on harmonic balance method

YANG Ronggang, AN Zijun

(College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

In order to reveal the nonlinear dynamics behavior of the equal speed output mechanism of cycloid ball planetary transmission, a pure torsion strongly nonlinear dynamics model was established in consideration of different number of balls, input excitation, different stiffness and different engagement state. Expressing the vice engagement preload function in a polynomial form and the vice engagement gap function in a describing function form, the harmonic balance method was used to convert the differential equations into nonlinear algebraic equations, which were solved by MATLAB, and the steady-state response of the system at foundamental frequency was obtained. The nonlinear dynamic characteristics were analyzed by changing the influential parameters such as the number of balls, axial compression and mesh stiffness. The results show that only two frequency orders of resonances of the preload system are stimulated. The nonlinear degree of the system decreases with the increase of the number of steel balls, the mesh stiffness and the preload. Preload is the most prominent factor affecting the degree of nonlinearity. The number of resonant frequencies of the gap system is related to the number of steel balls. The amplitude-frequency response curve shows the typical non-linear characteristics, and also shows the appearance of unilateral and bilateral impacts. The harmonic balance method based on polynomial function provides an effective method for the further study of the dynamic characteristics of cycloid ball planetary drives.

cycloid ball planetary transmission; equal speed output mechanism; harmonic balance method; amplitude-frequency characteristics; axial preload; nonlinear vibration

国家自然科学基金资助项目(51275440)；河北省自然科学基金资助项目(E2013203085)

2015-09-28 修改稿收到日期：2015-11-26

杨荣刚 男，博士生，1988年8月生

安子军 男，博士，教授，博士生导师，1960年2月生

TH113.1

A

10.13465/j.cnki.jvs.2017.02.025